Применение ультразвука в медицине
Под редакцией К. Хилла
Перевод с английского под редакцией д-ра техн. наук Л. Р. Гаврилова и д-ра физ.-мат. наук А. П. Сарвазяна
Оглавление
Предисловие редакторов перевода
Глава 1. Теоретические основы акустики (Э. Миллер)
1.2. Основные соотношения и определения линейной акустики
1.3. Простейшие виды бегущих волн
1.3.2. Сферические бегущие волны
1.3.3. Цилиндрическая симметрия
1.4.1. Модель фазированной решетки
1.5. Распределенные гармонические источники и угловой спектр плоских волн
1.5.1. Определение углового спектра плоских волн
1.5.2. Средняя по времени мощность излучения распределенного гармонического источника
1.5.3. Связь с диаграммой направленности в дальней зоне
1.6. Нестационарные поля излучения распределенных источников
1.7. Одномерное волновое движение
1.7.1. Связь параметров акустической волны со свойствами материала
1.7.2. Отражение и прохождение при нормальном падении
1.7.4. Прохождение через пластинку (нормальное падение)
1.8. Нелинейные эффекты в жидких средах без потерь
Глава 2. Генерация акустических полей и их структура (К. Хилл)
2.2. Пьезоэлектрические преобразователи
2.3. Импульсные акустические поля
2.4.2. Поля преобразователей краевых волн и аксиконов
2.5. Формирование пучков с помощью решеток преобразователей
2.6. Акустическое поле гибридной системы «Торонто»
2.7. Генерация акустических полей для терапии
Глава 3. Прием и измерение ультразвука (Э. Миллер, К. Хилл)
3.2. Пьезоэлектрические устройства
3.2.1. Калибровка гидрофона методом взаимности
3.2.2. Методы проведения измерений в точке
3.4. Измерения радиационного давления
3.4.1. Измерения с большой мишенью
3.4.2. Измерения с малой мишенью
3.6. Методы оптической дифракции
3.7. Другие методы приема и измерения звука
3.8. Измерение биологически эффективных экспозиций и доз
Глава 4. Затухание и поглощение ультразвука (Дж. Бэмбер)
4.2. Сечения взаимодействия ультразвуковой волны с биологической тканью
4.3. Анализ механизмов поглощения продольных ультразвуковых волн
4.3.1. Однородные водоподобные среды
4.3.2. Вязкоупругие свойства квазитвердых сред
4.3.5. Зависимость затухания от температуры
4.3.6. Влияние внешнего давления
4.3.7. Взаимосвязь явлений поглощения, дисперсии, затухания и рассеяния звука
4.4. Измерение коэффициентов затухания и поглощения в биологических тканях
4.4.2. Проблемы, связанные с артефактами и погрешностями измерений
4.5. Обзор литературных данных о коэффициентах затухания и поглощения
4.5.1. Биологически «простые» среды
Глава 5. Скорость звука (Дж. Бэмбер)
5.2. Измерение скорости ультразвуковых волн в биологических тканях
5.2.2. Проблемы, артефакты и погрешности
5.3. Анализ опубликованных данных о скорости звука
5.3.2. Зависимость скорости звука от температуры и давления
5.3.3. Влияние структурных компонентов ткани
Глава 6. Отражение и рассеяние ультразвука (Р. Дик и неон)
6.1.2. Современное состояние теории рассеяния
6.1.3. Рассеяние волн произвольной природы
6.2.3. Решение для одиночного препятствия
6.2.4. Дифракционная теория для совокупности рассеивателей
6.3. Рассеяние в случайно-неоднородных средах
6.3.1. Модели биологических тканей
6.3.2. Модель дискретных рассеивателей
6.3.3. Модель неоднородного континуума
6.4. Экспериментальное исследование рассеяния
6.4.2. Взаимосвязь между полным сечением рассеяния и затуханием
6.4.3. Зависимость сечения рассеяния от частоты
6.4.4. Угловая зависимость коэффициентов рассеяния
6.4.5. Влияние различных компонентов тканей
6.5. Рассеяние импульсных сигналов
6.5.1. Основы теории: импульсная характеристика ткани
6.5.2. Свойства изображений, получаемых при В-сканировании
6.5.3. Пространственно-временная корреляция эхо-сигналов
6.6.1. Профили коэффициента отражения и акустического импеданса
6.6.2. Взаимосвязь с рассеянием
ЧАСТЬ II. МЕТОДЫ ВИЗУАЛИЗАЦИИ И ИССЛЕДОВАНИЯ
Глава 7. Визуализация в медицине (К. Хилл)
7.2. Количественные описания при получении и восприятии изображения
7.2.1. Измерение амплитуды отображаемого сигнала
7.2.2. Меры пространственных характеристик систем визуализации
7.3. Характеристики зрительного восприятия человека
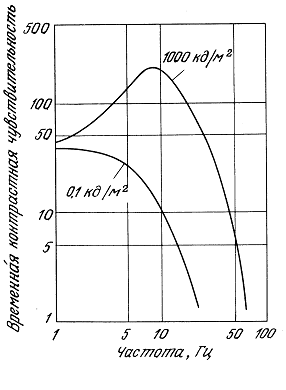
7.3.1. Острота зрения и восприятие яркостного контраста
7.3.2. Фактор времени в зрительном восприятии
7.4. Место ультразвука в медицинской визуализации
7.5. Систематика интерпретации изображений
Глава 8. Эхо-импульсные методы визуализации и измерений (К. Хилл)
8.2. Режимы представления эхо-импульсной информации
8.4. Сложное сканирование и некогерентность изображения
8.5. Влияние среды распространения
8.6.3. Обработка информации для отображения
8.7. Ограничение скорости сканирования и частоты кадров
8.8. Испытания и оценка характеристик систем
8.9. Области применения эхо-импульсных
8.9.3. Исследование внутренних органов
8.9.4. Приповерхностные и наружные органы
Глава 9. Прочие методы визуализации (К. Хилл)
9.2. Двумерная регистрация акустического изображения
9.3. Трансмиссионная визуализация
9.4. Трансмиссионная реконструктивная визуализация полей затухания и скорости звука
9.5. Визуализация в режиме обратного рассеяния с реконструкцией по двум параметрам
Глава 10. Телегистология (К. Хилл)
10.2. Использование объемных характеристик исследуемой ткани
10.3. Использование признаков эхограммы
10.4. Использование характеристик рассеяния на тканях
10.5. Использование параметров движения тканей
Глава 11. Доплеровские методы (П. Фиш)
11.3. Доплеровский прибор непрерывного излучения
11.4. Импульсно-доплеровский измеритель скорости кровотока
11.5. Анализ спектра доплеровского сигнала
11.5.2. Спектр импульсно-доплеровского сигнала
11.5.3. Форма спектра доплеровского сигнала
ЧАСТЬ III. БИОФИЗИКА УЛЬТРАЗВУКОВЫХ ЭФФЕКТОВ И ИХ ПРИМЕНЕНИЕ
Глава 12. Биофизика ультразвуковых эффектов (Г. тер Хаар)
12.1.2. Экспериментальные наблюдения температурных распределений
12.2.5. Экспериментально измеренные пороги кавитации
12.3. Радиационное давление, акустические течения и другие нетепловые механизмы
12.3.4. Акустические микропотоки вокруг пузырька
12.3.5. Другие нетепловые эффекты
12.3.6. Силы взаимодействия частиц
12.4. Некавитационные источники сдвиговых напряжений
12.5. Наблюдения эффектов нетепловой природы в структурированных тканях
Глава 13. Применение ультразвука в терапии и хирургии (Г. тер Хаар)
13.2. Физиологические основы ультразвуковой терапии
13.3.1. Оборудование и методики
13.3.2. Использование ультразвука в физиотерапии
13.4.1. Хирургия с помощью фокусированного ультразвука
13.4.3. Инструментальная ультразвуковая хирургия
13.5. Ультразвук при лечении рака
Глава 14. Оценка безопасности применения ультразвука в медицине (Г. тер Хаар)
14.2. Практика и уровни облучения
14.3. Исследования на изолированных клетках
14.3.3. Изменения ультраструктуры клеток
14.3.4. ДНК и генетические эффекты
14.3.5. Функциональные изменения
14.4. Исследования на многоклеточных организмах
14.4.1. Эффекты в костях и мягких тканях
14.4.2. Воздействие на кровь и кровеносные сосуды
14.4.3. Последствия ультразвукового облучения эмбрионов
14.4.4. Ультразвук в онкологии
14.5. Исследования эмбрионов человека
14.6. Краткие рекомендации и указания по режимам облучения
Давно известно, что ультразвуковое излучение можно сделать узконаправленным. Еще в период первой мировой войны в военно-морском флоте предпринимались попытки использовать направленный ультразвук для целей подводной локации. Во время этих экспериментов французский физик Поль Ланжевен впервые заметил повреждающее действие ультразвукового излучения на живые организмы. Результаты его наблюдений, а также сведения о том, что ультразвуковые волны могут проникать сквозь мягкие ткани человеческого организма, привели к тому, что с начала 1930-х гг. возник большой интерес к проблеме применения ультразвука для терапии различных заболеваний. Этот интерес не ослабевал и в дальнейшем, причем развитие медицинских приложений шло по самым разным направлениям; особенно широко ультразвук стал применяться в физиотерапии. Тем не менее лишь сравнительно недавно стал намечаться истинно научный подход к анализу явлений, возникающих при взаимодействии ультразвукового излучения с биологической средой.
Толчком к существенному развитию ультразвуковых диагностических методов явилось создание быстродействующих электронных импульсных систем обработки радиолокационных сигналов. Такие системы стали широко внедряться в радиолокации в период второй мировой войны 1939—1945 гг. Однако большинство первоначальных попыток применения ультразвуковых методов в диагностике носило в основном эмпирический характер. Лишь сравнительно недавно эта область приложений ультразвука получила признание как самостоятельная (и весьма увлекательная) область прикладной физики. Однако как практическое средство медицинского обследования ультразвук завоевал к настоящему времени весьма прочное положение. Оценки показывают, что сейчас ежегодное ультразвуковое обследование во всем мире проходят примерно 30—50 млн. пациентов и их число увеличивается каждый год приблизительно на 20%. Эти цифры свидетельствуют о том, что по широте своего использования в качестве физического диагностического средства ультразвук приблизился к рентгеновским методам.
Предисловие
Следует отметить, что ультразвуковые методы начинают становиться на прочную научную основу.
Ранее уже был издан ряд прекрасных книг и пособий, посвященных вопросам применения ультразвука в медицине. Следует, однако, отметить, что в большинстве из них основное место занимает описание накопленных экспериментальных данных. В предлагаемой читателю книге предпринята попытка исследовать возможности медицинского применения ультразвука, исходя из физических принципов. С этих позиций мы не ставили себе целью создать справочное руководство, которое позволило бы быстро, но недостаточно критично воспользоваться достижениями современной ультразвуковой техники и технологии. Мы стремились (по-видимому, впервые) осветить данную тему по возможности логически последовательно, чтобы помочь тем читателям, которые еще только входят в эту тематику, достичь в ней успехов.
По своей сути распространение ультразвука представляет собой типичный волновой процесс, поэтому в гл. 1 детально излагаются основные понятия и методы волновой акустики. Для людей, склонных к аналитическим исследованиям, представленный основополагающий материал может послужить неким отправным моментом для более глубокого изучения интересующих их частных вопросов. Для специалистов, занимающихся прикладными задачами, он раскрывает общие принципы, применение которых рассматривается в последующих главах. Гл. 2 посвящена теоретическому анализу акустических полей. Здесь рассматривается пространственная структура некоторых конкретных полей и дается описание методов генерации таких полей. Вообще говоря, интерес к использованию ультразвука в медицине и биологии обусловлен, во-первых, возможностью проведения с помощью ультразвуковых волн активного воздействия на живые ткани и, во-вторых, возможностью получения определенной информации о самих тканях. Эта информация может быть закодирована в самом ультразвуковом поле в результате различных взаимодействий этого поля с исследуемой средой. В обоих случаях необходимо уметь измерять характеристики ультразвукового поля. Описанию различных способов измерения полей посвящена гл. 3. В первых трех главах обсуждение полученных результатов проводится в основном при упрощающем допущении о том, что рассматриваемая среда является однородной и в ней отсутствуют потери акустической энергии. Как правило, в реальных средах, и особенно в тканях человеческого организма, это предположение далеко не соответствует истинной картине, поэтому в следующих трех главах проводится анализ физических параметров реальных тканей. Здесь представлены результаты теоретических и экспериментальных исследований механизмов затухания ультразвука, факторов, влияющих на скорость звука и ее изменение, а также процессов отражения и рассеяния ультразвуковых волн.
Вторая часть книги посвящена тем приложениям ультразвука, которые обычно принято называть «диагностическими». Здесь значительное место уделено практическим методам акустической «визуализации», суть которой заключается в представлении полученной информации об исследуемом объекте (например, о каких-либо участках в теле пациента) в виде изображений, позволяющих определить пространственное местоположение этого объекта и обеспечивающих возможность их визуального восприятия и анализа непосредственно человеком. Поскольку процесс визуального восприятия играет ключевую роль при анализе как обычных, так и акустических изображений, он рассматривается отдельно в короткой вступительной главе второй части книги. В большинстве практических приложений ультразвука в диагностике используется эхо-импульсный метод. Вопросы, связанные с его применением, широко освещены в целом ряде книг и обзоров, поэтому в гл. 8 настоящей книги мы ограничились обсуждением основных принципов этого метода и его возможностей в наиболее важных медицинских приложениях. В гл. 9 рассматриваются различные способы получения изображений, где наряду со ставшим уже «классическим» эхо-импульсным методом визуализации обсуждаются и некоторые новые подходы к получению акустических изображений анатомических структур. В этой главе рассматриваются также вопросы, связанные с акустической микроскопией. Традиционно разработчики медицинских систем акустической визуализации стремились к тому, чтобы представить информацию, полученную об исследуемых анатомических структурах, в виде изображения, которое опытный оператор мог бы рассмотреть и сделать определенные качественные заключения. В последнее время широко стали исследоваться возможности получения на основе акустической визуализации количественных (объективных) данных, которые дополняли бы информацию, воспринимаемую непосредственно человеческим глазом и мозгом при анализе изображений. Исследование таких возможностей является предметом телегистологии, или «характеризации тканей», которая рассматривается в гл. 10. Следует подчеркнуть, что для целей телегистологии применение ультразвука представляется особенно многообещающим. Заключительная глава этой части книги посвящена методам измерения и анализа кровотока, в основе которых лежит применение специализированной обработки сигналов с использованием эффекта Доплера.
Как уже отмечалось, при определенных условиях ультразвуковое воздействие может привести к видоизменению тех клеток и тканей, через которые распространяются ультразвуковые волны. Три заключительные главы книги посвящены обзору тех явлений, которые происходят при активном ультразвуковом воздействии на биологическую среду. Здесь рассматриваются также практические последствия такого воздействия. Гл. 12 описывает биофизические аспекты действия ультразвука, а именно те механизмы, посредством которых акустическое воздействие приводит к заметному биологическому эффекту. В гл. 13 мы попытались дать научную оценку различным признанным и разрабатываемым приложениям ультразвука в терапии и хирургии. Другими словами, речь здесь идет о тех областях применения, где биологические изменения создают преднамеренно. В последней главе рассмотрен ряд вопросов, связанных с безопасностью активного ультразвукового воздействия для пациентов и обслуживающего персонала при проведении различных медицинских процедур.
Благодарности. Выход в свет данной книги был бы невозможен без совместных усилий со стороны многих людей, принимавших непосредственное участие в ее написании и в подготовке рукописи к печати. Я очень признателен моим соавторам за творческое сотрудничество и проявленное упорство, без которых поставленная цель вряд ли была бы достигнута. В значительной степени в книге отражены научные интересы нашей собственной исследовательской группы, а также некоторые результаты ее работы за последние двадцать лет. Высоко ценю тот вклад в развитие медицинской акустики, который внесли за этот период мои коллеги, студенты и приглашенные сотрудники других групп, но, к сожалению, не всегда на страницах книги удалось в должной мере отразить их участие. Работы в данной области стали возможны благодаря поддержке со стороны Института онкологических исследований и Королевского госпиталя Марсдена, а также их финансирующих организаций, в частности Совета по медицинским исследованиям и Секции исследования рака. Мне хотелось бы выразить им большую благодарность. Неоценимую помощь при подготовке текста и иллюстративного материала оказали Луиза Паркес, Аннабел Томас и Джек Карент.
ФИЗИЧЕСКИЕ ОСНОВЫ
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АКУСТИКИ
Распространение волн —это физическое явление, на котором основаны все методы и применения ультразвука в медицине. В настоящей книге сделана попытка, исходя из физических основ, выделить принципы и практические результаты, достигнутые в этой большой области, лежащей на стыке разных наук.
Основы волновой физики знакомы большинству читателей книги, и с учетом этого первая глава преследует несколько целей. Во-первых, она призвана напомнить читателям принятые обозначения и методологию. Во-вторых, в ней мы рассмотрим ограничения и приближения, необходимые для решения некоторых задач биомедицинской акустики. Втретьих, попытаемся представить краткий обзор математического аппарата, необходимого для решения ключевых задач в ряде тесно связанных разделов акустики — от создания решеток излучателей до физических основ эффекта радиационного давления, которые затем будут использованы при анализе проблемы измерений полной средней по времени мощности (см. гл. 3).
В одной главе бессмысленно даже пытаться дать сколь-нибудь полное и строгое исследование акустической теории, поэтому отсылаем читателя к работам Тёрстона [29], Морса и Ингарда [21], Кинслера и Фрея [15], Найборга [22]. Более упрощенное, но полезное исследование дано в работе Губермана [9].
Мы попытались сделать каждый раздел этой главы самостоятельным. Тема логически развивается от основных физических уравнений до получения полезных для практики результатов. Выбор темы до некоторой степени должен отражать привычки, интересы и опыт автора. Однако здесь сделана попытка выделить полезные и интересные темы, а также обеспечить понимание математического аппарата, существа допущений и проблем.
С применениями ультразвука в медицине связано множество разных аспектов. Однако, при этом физика явления должна включать следующие процессы: распространение ультразвука в «биологической среде», такой как тело человека, взаимодействие ультразвука с компонентами этой среды и (по крайней мере в диагностических приложениях) измерение и регистрация акустического излучения, как падающего на объект, так и возникающего в результате взаимодействия с ним.
Проблема интерпретации взаимодействия акустического излучения с биологической средой существенно упрощается, если последнюю рассматривать не как твердое тело, а как жидкость. В такой среде нет сдвиговых волн, поэтому теория распространения волн проще, чем для твердого тела. В диапазоне ультразвуковых частот, применяемых в медицинской акустике, это предположение справедливо почти для всех тканей тела, хотя имеются и исключения, например кость. Следствия такого подхода рассмотрены в последующих главах. То, что взаимодействие ультразвука с тканью можно смоделировать его взаимодействием с жидкостями, — важный фактор, повышающий практическую ценность медицинской ультразвуковой диагностики.
С учетом реального отношения сигнал/шум эффективная глубина проникновения ультразвука в мягкие ткани (определенная как величина, обратная коэффициенту затухания по амплитуде) составляет около 100 длин волн. Этот факт влияет на конструкцию аппаратуры и обязательно учитывается при моделировании. С одной стороны, это означает, что можно применять устройства аподизации, фокусировки и сканирования пучка для направленной передачи акустической энергии, ограничения объема цели и уменьшения ее неоднозначности. Эти методы хорошо известны в различных областях оптики, радиолокации и акустической локации. С другой стороны, высокое отношение глубины проникновения к длине волны означает, что в первом приближении уравнения распространения можно решать без учета рассеяния и затухания.
Чтобы избежать сложностей теории распространения акустических импульсов, описание работы акустических излучателей обычно ограничивают непрерывным режимом. Между тем в большинстве медицинских диагностических приборов используются именно импульсные излучатели, генерирующие несколько периодов колебаний. Уметь моделировать и описывать такой сигнал очень важно. Например,известно, что продольное разрешение излучателя (в отличие от азимутального или поперечного) зависит от длительности импульса. Известно также, что при излучении коротких импульсов уменьшаются боковые лепестки и изрезанность структуры поля по сравнению с непрерывной волной. Боковые лепестки и изрезанность ухудшают качество изображения, так как приводят к неоднозначности цели или к снижению поперечного разрешения.
В этой главе рассматривается теоретическое описание распространения импульса, что отражается на выборе математического аппарата (в частности, используется преобразование Лапласа, а не Фурье). Ясно, что из-за большого числа независимых переменных, включаемых в описание нестационарного звукового поля при использовании более строгих теоретических методов, теряется их гибкость и наглядность. Более приближенный модельный подход может оказаться достаточным для решения сложных инженерных задач, таких как описание работы решеток преобразователей в импульсном режиме.
Общее предположение в излагаемой теории — линейность, т. е. прямая пропорциональность между приложенным к среде напряжением в акустической волне и соответствующим смещением ее частиц. Однако, уравнения механики жидкости по нескольким причинам изначально нелинейны. Например, нелинейность может проявиться в уравнениях без потерь или с потерями, вызванными поглощением. Таким образом, говоря о нелинейности, необходимо определить задачу и конкретный механизм. Хотя многие явления, встречающиеся в медицинской эхо-импульсной диагностике, могут быть описаны в линейном режиме, мы увидим, что появляется ряд существенных отклонений от линейности. В частности, учет нелинейности требуется для описания радиационного давления — основы одного из простейших и удобных методов измерения полной усредненной по времени мощности направленного акустического излучения (описание метода см. в гл. 3).
Почти во всей главе рассматривается теория в простейшем приближении однородной среды без дисперсии и потерь. Однако практический интерес представляет «реальная» среда, для которой эти условия не выполняются. Акустические свойства сред, встречающихся в медико-биологической практике, описываются в гл. 4—6.
1.2. ОСНОВНЫЕ СООТНОШЕНИЯ И ОПРЕДЕЛЕНИЯ ЛИНЕЙНОЙ АКУСТИКИ
Приведенные ниже уравнения могут служить отправной точкой при решении тех задач линейной акустики, в которых пренебрегают потерями энергии. Предполагается, что в жидкости малы отклонения от состояния равновесия. Стационарные потоки из рассмотрения исключаются. Запишем уравнение неразрывности
![]()
и уравнение движения
![]()
В этих уравнениях р — линейное возмущение давления, связанное с возмущением скорости частицы v; с—скорость звука; ![]() — плотность невозмущенной жидкости; t — независимая временная координата. Символ
— плотность невозмущенной жидкости; t — независимая временная координата. Символ ![]() — обыкновенный векторный дифференциальный оператор в обозначениях Гиббса. Например, в декартовых координатах
— обыкновенный векторный дифференциальный оператор в обозначениях Гиббса. Например, в декартовых координатах
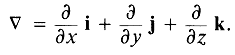
Однако обозначения Гиббса универсальны, и аналогичные выражения существуют также в криволинейной системе координат.
Уравнение неразрывности — выражение закона сохранения массы для сплошных сред, а уравнения движения — выражение второго закона Ньютона для этих сред.
Не меняя физического смысла уравнений (1.1) и (1.2), число переменных можно уменьшить, введя обозначения

Символ ![]() используется для обозначения того, что правая часть выражения есть определение левой. Уравнения (1.5) и (1.6) —это уравнения (1.1) и (1.2) в координатах
используется для обозначения того, что правая часть выражения есть определение левой. Уравнения (1.5) и (1.6) —это уравнения (1.1) и (1.2) в координатах ![]() и
и ![]() :
:

Кажущаяся симметрия р и ![]() в уравнениях (1.5) и (1.6) может затенить то, что в действительности (1.6) содержит три уравнения. Итак, выражения (1.5) и (1.6) составляют систему четырех уравнений с четырьмя неизвестными.
в уравнениях (1.5) и (1.6) может затенить то, что в действительности (1.6) содержит три уравнения. Итак, выражения (1.5) и (1.6) составляют систему четырех уравнений с четырьмя неизвестными.
Здесь удобно ввести скалярный потенциал скорости ![]() , определяемый равенствами
, определяемый равенствами

причем уравнение (1.6) сводится к тождеству сменой порядка дифференцирования по времени и пространству. Уравнение (1.5) становится волновым уравнением для ![]() :
:
![]()
где лапласиан ![]() ив декартовых координатах определяется выражением
ив декартовых координатах определяется выражением
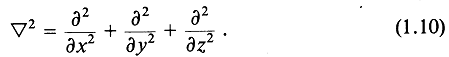
Зная решение (1.9) для ![]() , из уравнений (1.7) и (1.8) можно определить р и
, из уравнений (1.7) и (1.8) можно определить р и ![]() . Решения для
. Решения для ![]() зависят от граничных и начальных условий.
зависят от граничных и начальных условий.
Задачи линейной акустики можно также представить в виде волнового уравнения для давления, не рассматривая потенциал скорости. Это волновое уравнение получается при дифференцировании по ![]() уравнения (1.5) и умножении обеих частей (1.6) на дифференциальный оператор
уравнения (1.5) и умножении обеих частей (1.6) на дифференциальный оператор ![]() .
.
Изменяя порядок дифференцирования по времени и пространству и подставляя в (1.6) выражение для ![]() , получим волновое уравнение для давления:
, получим волновое уравнение для давления:
![]()
Уравнения (1.11) и (1.6) образуют систему, эквивалентную уравнениям (1.7) —(1.9).
Так как большая часть аппаратуры, используемой в медицинской диагностике, основана на принципах импульсной эхолокации, представляет интерес математическое описание нестационарных звуковых полей. Непосредственно из уравнения (1.7) следует важный вывод о поведении коротких импульсов типа ударной волны в линейных однородных средах без потерь. Для этого запишем уравнение (1.7) в интегральной форме:
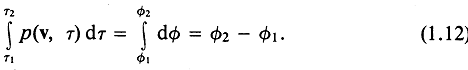
Для случая короткого импульса величина ![]() в любой точке
в любой точке ![]() покоящейся жидкости до прихода импульса
покоящейся жидкости до прихода импульса ![]() равна величине
равна величине ![]() в покоящейся жидкости после прохождения импульса
в покоящейся жидкости после прохождения импульса ![]() . Тогда
. Тогда

Из уравнения (1.13) видно, что среднее по времени давление для всего импульса должно равняться нулю. Это согласуется с наблюдением, что волн только сжатия или только разрежения не существует.
Предыдущие уравнения и условия указывают метод определения давления и скорости частиц в акустическом поле как функций пространства и времени. Связь между этими двумя переменными акустического поля и акустической мощностью (интенсивностью) мы объясним чуть позже. Само объяснение этих соотношений следует из уравнений (1.5) и (1.6) после некоторых алгебраических преобразований и применения теоремы Гаусса (теоремы о дивергенции).
Заметим, что уравнения (1.5) и (1.6) умножением на соответствующие переменные можно привести к виду
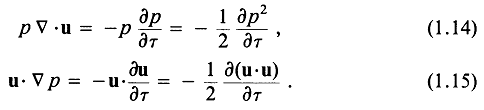
Отметим также следующее тождество:
![]()
Объединяя уравнения (1.14), (1.15) и (1.16), получаем
![]()
Используем теперь теорему Гаусса, чтобы получить интегральную форму уравнения (1.17) для объема V без источников и стоков, ограниченного поверхностью S:
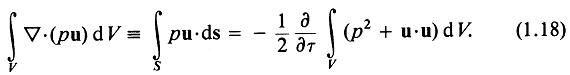
В обозначениях (1.1) и (1.2) получаем
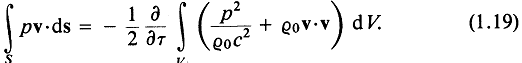
Из соображений размерности видно, что
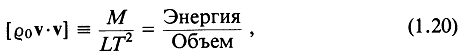
где М, L и Т— размерности массы, длины и времени, а квадратные скобки обозначают размерность заключенного в них выражения.
Таким образом, уравнение (1.19) означает, что скорость потери энергии в объеме равна интегралу проекции рv на внешнюю нормаль по всей поверхности, ограничивающей этот объем. Так как мощность — это энергия в единицу времени, рv имеет размерность мощности на единицу площади (или интенсивности).
Действительно, акустическая интенсивность ![]() определяется как
определяется как
![]()
а плотность акустической энергии Е> связанная с уравнениями (1.1)
и (1.2), как
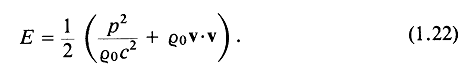
Можно глубже исследовать выражения для ![]() и Е, включая члены высших порядков в разложении существенно нелинейных уравнений гидродинамики (см. разд. 1.8).
и Е, включая члены высших порядков в разложении существенно нелинейных уравнений гидродинамики (см. разд. 1.8).
Основы изложенного здесь материала можно найти в работах [1, 8, 16, 21, 25].
1.3. ПРОСТЕЙШИЕ ВИДЫ БЕГУЩИХ ВОЛН
В этом разделе мы рассмотрим три простых типа бегущих волн. Будут выведены уравнения, описывающие волны, у которых поверхности равной фазы и равной амплитуды являются плоскими, сферическими или цилиндрическими.
Термин «простой источник» часто означает идеальный генератор одного из этих видов бегущих волн. Например, можно представить, что плоские волны порождаются бесконечной плоскостью, движущейся по перпендикуляру к своей поверхности.
Аналогично, сферические волны порождаются поверхностью сферы при радиально симметричном движении, а цилиндрические — поверхностью бесконечно длинного кругового цилиндра, движущегося радиально симметрично (т. е. независимо от координаты, направленной вдоль оси симметрии цилиндра).
Будем рассматривать бегущие волны в линейной жидкости без потерь, описываемой уравнениями (1.7), (1.8) и (1.9). Уравнение (1.9) (волновое уравнение для ![]() ) решается преобразованием Лапласа по независимой переменной
) решается преобразованием Лапласа по независимой переменной ![]() при соответствующих начальных и граничных условиях.
при соответствующих начальных и граничных условиях.
Преобразование Лапласа от функции ![]() имеет вид
имеет вид
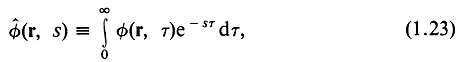
где s — комплексная переменная в пространстве образа Лапласа. Символами ![]() и
и ![]() будем обозначать первую и вторую производные
будем обозначать первую и вторую производные ![]() по
по ![]() .
.
Образы производных ![]() по
по ![]() связаны с образом
связаны с образом ![]() (
(![]() ) -следующими выражениями, содержащими в явном виде начальные условия:
) -следующими выражениями, содержащими в явном виде начальные условия:
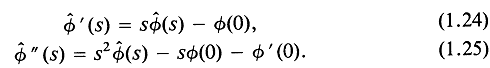
Выражения (1.24) и (1.25) справедливы при условиях непрерывности ![]() и
и ![]() при
при ![]() и существования
и существования ![]() и
и ![]() при
при ![]() — некоторое значение).
— некоторое значение).
Применяя (1.23) — (1.25) для преобразования Лапласа от выражений (1.7) — (1.9), получаем при условиях: ![]()
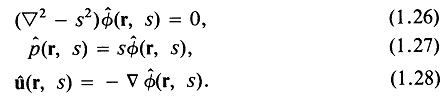
Выражение для ![]() , получаемое при решении (1.26) с соответствующими граничными условиями, позволяет с помощью (1.27) и (1.28) найти
, получаемое при решении (1.26) с соответствующими граничными условиями, позволяет с помощью (1.27) и (1.28) найти ![]() и
и ![]() , которые затем подвергаются обратному преобразованию для получения
, которые затем подвергаются обратному преобразованию для получения ![]() и
и ![]() .
.
Упрощенное уравнение вида (1.26) для случая бегущих плоских волн, фазовый фронт которых ориентирован по нормали к оси z, имеет вид

Решение (1.29) записывается в виде
![]()
Если наложить условие конечности ![]() при больших z, уравнение (1.30) приводится к виду
при больших z, уравнение (1.30) приводится к виду
![]()
Тогда из (1.27) и (1.28) получаем
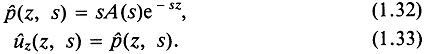
Отметим, что
![]()
Если определить ![]() :
:
![]()
то обратное преобразование уравнений (1.34) и (1.35) (например, с использованием таблицы пар образов) дает
![]()
Здесь ![]() — обобщенная функция, называемая иногда функцией единичного скачка. По определению,
— обобщенная функция, называемая иногда функцией единичного скачка. По определению,
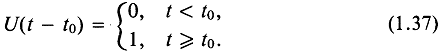
Аргумент функции F в уравнении (1.36) пропорционален так называемому запаздывающему времени (т. е. t - z/c).
Из определения акустической интенсивности ![]() (уравнения (1.21) и (1.36)) видно, что z-компонента интенсивности для плоской волны, распространяющейся вдоль z, есть
(уравнения (1.21) и (1.36)) видно, что z-компонента интенсивности для плоской волны, распространяющейся вдоль z, есть
![]()
Итак, получены выражения, связывающие акустические параметры с независимыми переменными (координатами и временем) для линейного распространения плоских волн без потерь. Распространение таких волн полностью описывается параметром, который пропорционален нормальной к волновому фронту составляющей скорости частиц vz и акустическому давлению р. Характер плоского акустического импульса полностью определяется зависящей от ![]() формой волны в начале координат (при z = 0). Жидкость в произвольной точке z1 (при z
формой волны в начале координат (при z = 0). Жидкость в произвольной точке z1 (при z ![]() 0) покоится до момента времени z1/c, после чего может наблюдаться импульс. Кроме того, из уравнения (1.36) очевидно, что в линейной однородной среде без потерь бесконечная плоская волна не ослабляется с увеличением z.
0) покоится до момента времени z1/c, после чего может наблюдаться импульс. Кроме того, из уравнения (1.36) очевидно, что в линейной однородной среде без потерь бесконечная плоская волна не ослабляется с увеличением z.
1.3.2. СФЕРИЧЕСКИЕ БЕГУЩИЕ ВОЛНЫ
Для сферически симметричных акустических волн можно получить аналогичные результаты после упрощения уравнений (1.26) и (1.28). В этом случае лапласиан представляется в виде
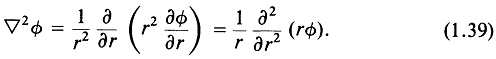
Тогда уравнение (1.26) принимает вид
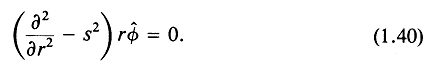
Решение для возникающей волны полностью аналогично случаю плоских волн (см. п. 1.3.1):
![]()
Из этого выражения и уравнений (1.27) и (1.28) получаем

Очевидно, значение ![]() при r = 0 физически бессмысленно, так как обращается в бесконечность. Ситуация проясняется, если ввести радиус конечного сферического источника: кстати, такой источник и должен реально существовать.
при r = 0 физически бессмысленно, так как обращается в бесконечность. Ситуация проясняется, если ввести радиус конечного сферического источника: кстати, такой источник и должен реально существовать.
Обозначая ![]() через
через ![]() , из (1.41) и (1.42) получаем
, из (1.41) и (1.42) получаем
![]()
Тогда
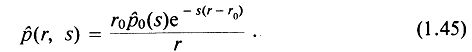
Более простой вид это выражение приобретает, если ввести в явном виде расстояние от поверхности источника
![]()
Тогда (1.45) можно переписать так:
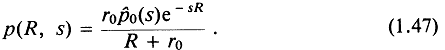
Обратное преобразование (1.47) с использованием таблицы пар образов дает
![]()
Если известно ![]() , то можно просто решить уравнение для скорости частицы. Ее радиальная составляющая равна
, то можно просто решить уравнение для скорости частицы. Ее радиальная составляющая равна ![]() , где
, где
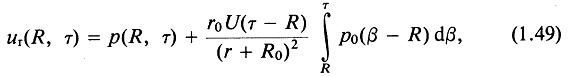
а ![]() — переменная интегрирования.
— переменная интегрирования.
Акустическое поле сферически симметричного возмущения полностью описывается давлением и радиальной составляющей скорости частиц. Выражение для акустической интенсивности более сложно, чем ![]() или
или ![]() (см. (1.38)) для бесконечной плоской волны. Это результат того, что в сферическом случае нормали к волновому фронту расходятся.
(см. (1.38)) для бесконечной плоской волны. Это результат того, что в сферическом случае нормали к волновому фронту расходятся.
В случае сферической симметрии радиальная компонента интенсивности определяется выражением
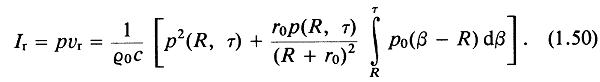
Итак, выражения для сферически-симметричных волн очень похожи на случай плоских волн. Основное различие состоит в геометрическом ослаблении волны давления, которое приводит к появлению дополнительного члена в выражении для скорости частиц. Ослабление возмущения давления на расстоянии r0 от сферического источника прямо пропорционально ![]() , где R — расстояние между источником и точкой измерения. Выражение для величины интенсивности звука сложнее, чем в случае плоской волны. Оно включает дополнительный член, вносимый скоростью частиц и связанный с тем, что с течением времени пространство объема, занимаемое волной, увеличивается или, другими словами, с расходимостью нормалей к поверхности фазового фронта.
, где R — расстояние между источником и точкой измерения. Выражение для величины интенсивности звука сложнее, чем в случае плоской волны. Оно включает дополнительный член, вносимый скоростью частиц и связанный с тем, что с течением времени пространство объема, занимаемое волной, увеличивается или, другими словами, с расходимостью нормалей к поверхности фазового фронта.
1.3.3. ЦИЛИНДРИЧЕСКАЯ СИММЕТРИЯ
Упрощение уравнения (1.26) для случая цилиндрических волн с круговой симметрией дает

Уравнение (1.51) можно переписать в виде, проясняющем математическую связь между цилиндрическими волнами, имеющими круговую симметрию, и уже рассмотренными видами волн. Это преобразование основано на следующем тождестве:
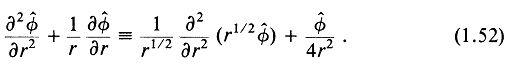
Поставляя (1.52) в (1.51), получаем
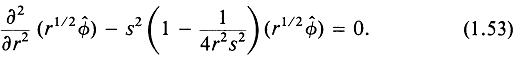
Для больших г уравнение (1.53) приводится к виду
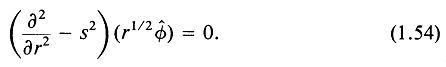
Как видно, уравнение (1.54) аналогично уравнению, полученному для волн со сферической симметрией, для которых оператор ![]() действовал на
действовал на ![]() . Таким образом, на больших расстояниях от начала координат основное различие между сферическими и цилиндрическими возмущениями состоит в скорости затухания бегущей волны.
. Таким образом, на больших расстояниях от начала координат основное различие между сферическими и цилиндрическими возмущениями состоит в скорости затухания бегущей волны.
Общее решение уравнения (1.51) выражается через функции Бесселя нулевого порядка:
![]()
функция ![]() при
при ![]() , а
, а ![]() при
при ![]() . Из требования ограниченности решения при
. Из требования ограниченности решения при ![]() получаем
получаем
![]()
При достаточно больших значениях х справедливо приближенное выражение для К0(х):
![]()
Если х = sr, то при больших r уравнение (1.56) становится аналогичным уравнению для сферической волны, что подтверждается переходом от (1.53) к (1.54).
Из уравнений (1.42) и (1.56) получаем выражение для волны
давления
![]()
Если теперь учесть (1.57), получим
![]()
Для удобства обозначим ![]() через
через ![]() и запишем
и запишем
![]()
Объединяя (1.59) и (1.60), получаем
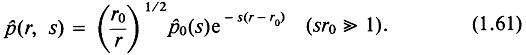
Как и в случае сферической волны, определим ![]() как расстояние от поверхности кругового цилиндрического источника с радиусом г0; тогда, используя обратное преобразование Лапласа,
как расстояние от поверхности кругового цилиндрического источника с радиусом г0; тогда, используя обратное преобразование Лапласа,
получаем
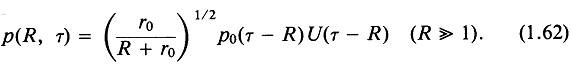
Отметим близкое сходство этого решения с выражением (1.48) для сферической симметрии, что и следовало ожидать вследствие сходства уравнений (1.54) и (1.40).
Общее решение уравнения (1.58) имеет вид
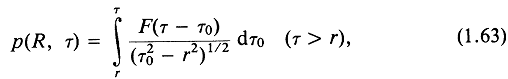
где F(![]() ) — обратное преобразование Лапласа от sA(s).
) — обратное преобразование Лапласа от sA(s).
В понимании смысла уравнения (1.63) может помочь замена переменных. Пусть ![]() , тогда
, тогда
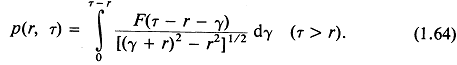
Вблизи фронта сформировавшегося бегущего цилиндрического возмущения при ![]() из уравнения (1.64) получаем
из уравнения (1.64) получаем
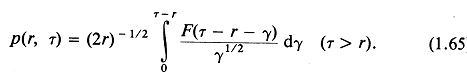
Обратим внимание на появление ожидаемой зависимости вида r-1/2 в выражении для давления и на вид интеграла с запаздыванием. Как и в случае сферической симметрии,
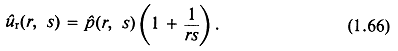
При больших значениях г0
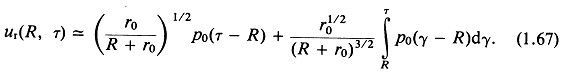
Из (1.62) и (1.67) получаем выражение для радиальной составляющей интенсивности
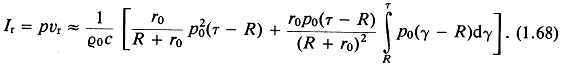
Итак, возмущения давления, порождаемые поверхностью бесконечного кругового цилиндра, движущегося радиально симметрично, не сохраняют свою первоначальную форму, как в случае плоских или сферических волн, а эволюционируют в соответствии с (1.63).
Однако для очень больших значений радиальной координаты возмущения давления ведут себя так же, как плоские и сферические волны (см. уравнения (1.54) и (1.55)). С физической точки зрения это объясняется тем, что рассматривается бесконечный круговой цилиндр. Любое нестационарное возмущение в точке r0 будет восприниматься в точке поля в течение времени, превышающего длительность возбуждающего возмущения, из-за протяженности
источника и конечной скорости распространения волны в среде. Возмущение давления существенно уменьшается из-за множителя ![]() , так что состояние жидкости в точке R не отличается от покоя, т. е. от ее состояния до прихода фронта нестационарной волны.
, так что состояние жидкости в точке R не отличается от покоя, т. е. от ее состояния до прихода фронта нестационарной волны.
Импульсы давления от длинного цилиндра обычно имеют длинные «хвосты». Хотя эти импульсы действуют с задержкой, они не воспроизводят первоначальный импульс источника, как это имеет место для бесконечного плоского излучателя или сферически-симметричного источника.
Уравнения (1.38), (1.50) и (1.68) выражают величину интенсивности как функцию пространства и времени для волн с особо простой геометрией (кроме того, в (1.68) величина R предполагается большой). Интересно также знать среднее по времени значение интенсивности. Действительно, при некоторых измерениях на ультразвуковых частотах, характерных для медицинских приложений, практически можно определить лишь средние по времени величины из-за инерционности аппаратуры и ограничений, налагаемых конструкцией датчика.
Для случая плоской волны усредненная по времени z-составляющая интенсивности (см. (1.38)):
где
![]()
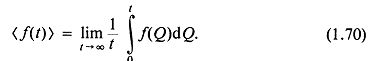
Здесь ![]() — произвольная функция времени, Q — переменная интегрирования.
— произвольная функция времени, Q — переменная интегрирования.
В случаях сферической и аксиальной симметрии выражения для интенсивности содержат члены вида
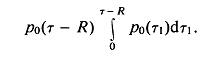
Если функция ![]() определяется как
определяется как
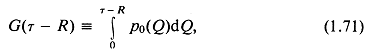
то по формуле Лейбница
![]()
Тогда
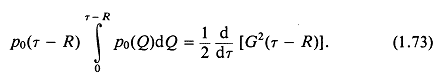
Среднее по г значение (тождественное среднему по t, что проверяется подстановкой в (1.70))
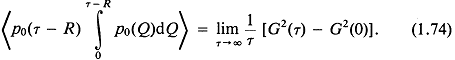
Так как, по определению, G(0) = 0 и интеграл по всей длительности волны ![]() также должен быть равен нулю, мы получаем, что среднее по
также должен быть равен нулю, мы получаем, что среднее по ![]() значение равно 0, даже без учета действия
значение равно 0, даже без учета действия ![]() при больших
при больших ![]() в уравнении (1.74).
в уравнении (1.74).
Таким образом, справедливы следующие выражения для средней по времени интенсивности импульса:
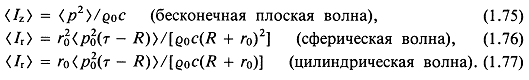
Результаты, полученные в разд. 1.3, широко применяются на практике при создании специальных конфигураций акустического поля, как будет качественно показано в гл. 2. Особенно важным оказывается применение этих результатов при разработке многоэлементных решеток [19, 27]. Поэтому в данном разделе мы проиллюстрируем приложение вышеприведенной теории к этой задаче. При таком конструировании возникает ряд вопросов —об относительном расположении элементов в пространстве [5.12], их относительных весах [6, 18, 24] и последовательности их подключения [5]. Решения этих конструкторских задач можно получить в рамках математической модели, позволяющей определять местоположение одиночных источников, задавать распределение амплитуды и фазы сигналов источников, а также последовательность подключения элементов.
Успешное применение такого модельного подхода требует ясного понимания всех приближений. В этом может помочь знание теории дискретизации информации [10, 23], но выбор приближений в уравнениях для полей отдельных источников будет также влиять на справедливость математической модели.
Уравнение (1.43) для сферических бегущих волн и уравнение (1.66) для цилиндрических волн имеют один и тот же вид
![]()
Уравнение (1.53) для цилиндрической волны имеет вид
![]()
Упрощения в этих уравнениях основаны на том, что расстояние от начала координат велико, так что ![]() . Для целых значений
. Для целых значений ![]() — оператор, связанный с дифференцированием по т того выражения, на которое он умножается, а
— оператор, связанный с дифференцированием по т того выражения, на которое он умножается, а ![]() — оператор, связанный с интегрированием сомножителя по т. Для рассмотренных выше, уравнений таким сомножителем является
— оператор, связанный с интегрированием сомножителя по т. Для рассмотренных выше, уравнений таким сомножителем является ![]() или
или ![]() .
.
Область допустимости приближения лучше всего оценивать по величине отношения отбрасываемого члена к остающемуся. Таким образом, отношение максимумов модулей этих членов — удобный показатель существенности отбрасываемого члена. Если рассмотреть уравнения (1.48) и особенно (1.49), которые получаются при обратном преобразовании Лапласа из уравнения (1.43), то при ![]()
![]()
где характерная длина / определяется как
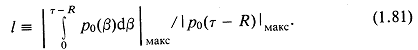
Оценки сходных приближений при ![]() (как в уравнении (1.53)) выполняются тем же способом и могут быть облегчены применением таблиц преобразования Лапласа.
(как в уравнении (1.53)) выполняются тем же способом и могут быть облегчены применением таблиц преобразования Лапласа.
1.4.1. МОДЕЛЬ ФАЗИРОВАННОЙ РЕШЕТКИ
Попытаемся теперь показать применимость вышеописанных положений к конкретной задаче: созданию математической модели решетки, состоящей из соосных сферических акустических источников.
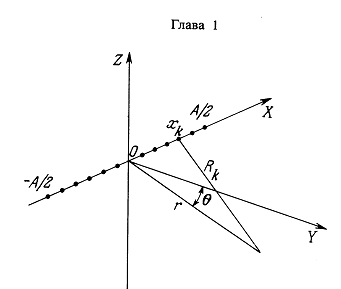
Рис. 1.1. Линейная решетка сферических источников: обозначения системы координат.
Практическая важность таких решеток источников будет показана в гл. 2 и 8. На рис. 1.1 представлены обозначения системы координат для этой модели. Предполагается, что источники излучают одинаковые импульсы давления и располагаются симметрично по обе стороны от центра решетки (x = 0) в положительном и отрицательном направлениях х. Предположим, что поле давления k-го источника задается следующим выражением:
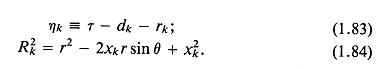
На рис. 1.2 показана осциллограмма такого импульса при М = 3 (М — длина импульса в единицах длины волны). Радиус источника, который обозначался в предыдущих разделах как r0, считается пренебрежимо малым. Задержки возбуждения сферических источников представлены в уравнении (1.83) как dk. Параметр ![]() — расстояние от центра решетки до произвольной точки поля; Rk — расстояние от k-го источника до этой же точки; Rk — координата k-го источника;
— расстояние от центра решетки до произвольной точки поля; Rk — расстояние от k-го источника до этой же точки; Rk — координата k-го источника; ![]() — длина волны в импульсе.
— длина волны в импульсе.
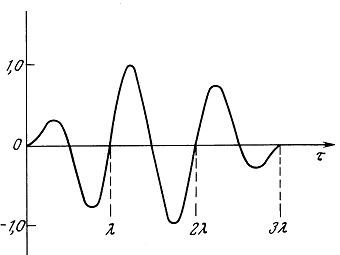
Рис. 1.2. Форма импульса при М = 3. Ордината описывается выражением
![]()
Предоставим читателю самостоятельно найти условия, при которых уравнение (1.49) упрощается до
![]()
Эти условия обсуждались в разд. 1.4. Из уравнения (1.49) видно, что выражение (1.85) с ростом расстояния становится все более точным.
Использование уравнений (1.82) — (1.85) зависит от понимания пространственных и временных соотношений между импульсами, излученными различными сферическими источниками. При акустических мощностях, применяемых в медицинском диагностическом оборудовании, можно считать, что принцип суперпозиции полей давления источников выполняется.
Можно представить две концентрические сферические поверхности с постоянным радиальным зазором ![]() , распространяющиеся от одиночного сферического источника со скоростью звука. Через время t от начала возбуждения первого источника акустический импульс от k-го элемента удалится на
, распространяющиеся от одиночного сферического источника со скоростью звука. Через время t от начала возбуждения первого источника акустический импульс от k-го элемента удалится на ![]() . В своей ближайшей к к-ыу источнику точке акустическое возмущение удалено от него на
. В своей ближайшей к к-ыу источнику точке акустическое возмущение удалено от него на ![]() . Обозначим эти расстояния
. Обозначим эти расстояния ![]() и
и ![]() и назовем их расстояниями от k-го источника соответственно до переднего и заднего фронтов k-го импульса. Если нарисовать двумерную диаграмму для этих фронтов в полярных координатах с началом в центре решетки (как в уравнении (1.84)), то можно вывести уравнения для
и назовем их расстояниями от k-го источника соответственно до переднего и заднего фронтов k-го импульса. Если нарисовать двумерную диаграмму для этих фронтов в полярных координатах с началом в центре решетки (как в уравнении (1.84)), то можно вывести уравнения для ![]() и
и ![]() в такой системе координат. При этом можно связать импульсы от отдельных сферических источников в решетке. Затем различные определения расстояний приравниваются и решаются квадратные уравнения относительно
в такой системе координат. При этом можно связать импульсы от отдельных сферических источников в решетке. Затем различные определения расстояний приравниваются и решаются квадратные уравнения относительно ![]() и
и ![]() . Эти рассуждения поясняются рис. 1.3.
. Эти рассуждения поясняются рис. 1.3.
Например, оказывается, что
![]()
Если считать все другие величины под корнем малыми по сравнению с ![]() , то множитель
, то множитель ![]() выносится из-под корня и для упрощения (1.86) и (1.87) используется разложение в ряд Тейлора.
выносится из-под корня и для упрощения (1.86) и (1.87) используется разложение в ряд Тейлора.
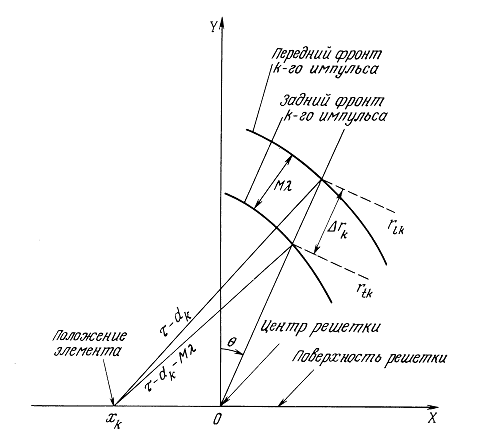
Рис. 1.3. Геометрия импульса, излученного отдельным элементом, в системе координат, связанной с центром решетки (x = 0, y = 0).
Границы k-го импульса в направлении ![]() приблизительно равны
приблизительно равны
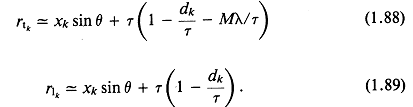
Проверяя расстояние между фронтами к-го импульса, получаем
![]()
Как видно, с точностью до разумных приближений можно считать, что импульсы от отдельных элементов имеют толщину MX в направлении 0, что очень упрощает сложение возмущений давления от разных источников.
Рассмотрим теперь расстояние между передним и задним фронтами импульсов от разных источников. Вычитание (1.88) из (1.89) дает
![]()
Разность (1.89) для двух различных источников дает другое полезное выражение:
![]()
Прежде чем рассмотреть общую модель решетки, необходимо выяснить лишь задержки возбуждения различных источников dk. Однако, если задержки и расположение элементов определены, этой информации достаточно, чтобы на ЭВМ построить диаграмму направленности. В конце вычислений суммируются вклады отдельных источников в произвольной точке поля в соответствии с принципом суперпозиции.
Для создания линейных решеток с электронным сканированием апертуры вдоль оси преобразователя важна фокусировка. Для создания фазированных решеток важны как фокусировка, так и управление пучком акустического излучения. Оба этих процесса можно ввести в уравнения с помощью задержек возбуждения источников dk. Далее мы определим выражения для этих задержек.
Произвольная нормаль, пересекающая линейную решетку источников в ее центре, и ось решетки определяют плоскость, в которой рассматриваются фокусировка и управление. Двумерные графики, поясняющие предыдущие уравнения, справедливы только вблизи этой плоскости. На практике это достаточно реальная модель, так как можно использовать статическую фокусировку, чтобы с точностью до дифракционных поправок ограничить акустическое излучение этой областью. В указанной плоскости излучение решетки будет сфокусировано на расстоянии R0 от ее центра. Угловое отклонение фокуса от нормали к решетке в ее центре обозначим через ![]() . С помощью геометрических построений можно показать, что для точечной фокусировки на расстоянии R0 с углом
. С помощью геометрических построений можно показать, что для точечной фокусировки на расстоянии R0 с углом ![]() .
.
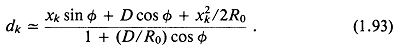
Рис. 1.4 может помочь в объяснении связи между параметрами в уравнении (1.93). Постоянную D можно определить, налагая условие, что внешний элемент (с координатой -А/1) обладает нулевой задержкой dk для максимального угла сканирования фт:
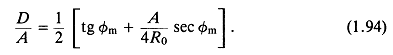
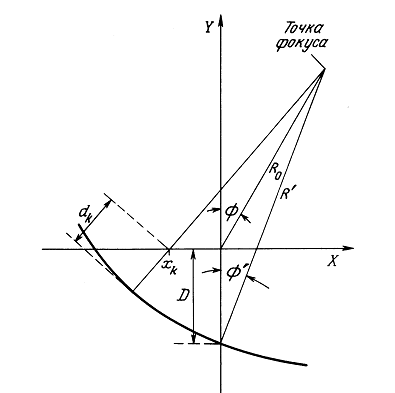
Рис. 1.4. Обозначения координат для сканирования луча с точечным фокусом.
Уравнение (1.93) можно привести к виду, удобному для оценки
уравнений (1.91) и (1.92):
![]()
где членом ![]() в знаменателе пренебрегают как малым.
в знаменателе пренебрегают как малым.
Тогда для сканируемой фокальной точки хорошим приближением (1.91) и (1.92) служат (1.96) и (1.97):
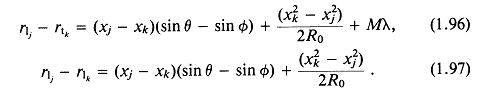
Из уравнения (1.96) видно, что толщина L огибающей результирующего возмущения давления в направлении ![]() зависит от угла сканирования
зависит от угла сканирования ![]() :
:
![]()
Теперь можно получить выражения для диаграммы направленности линейной решетки. Во-первых, необходимо определить систему координат, связанную с возмущениями давления. Для этого определим параметры, сведенные в рис. 1.5. Для заданного угла сканирования ![]() расстояние в направлении
расстояние в направлении ![]() между передним фронтом результирующего импульса и вкладом j-го сферического источника есть
между передним фронтом результирующего импульса и вкладом j-го сферического источника есть
![]()
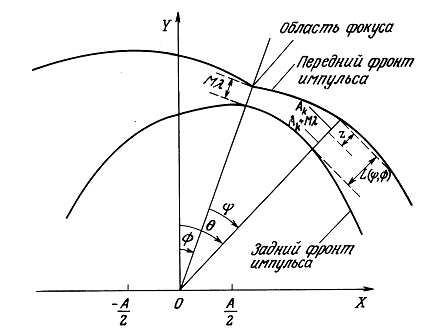
Рис. 1.5. Геометрия огибающей результирующего импульса. Показаны координаты, применяемые при описании внутренней структуры импульса.
с
Если z = 0 на переднем фронте результирующего импульса и нарастает к центру решетки, то
Тогда выражения давления и радиальной компоненты скорости частиц для сферических источников имеют вид
![]()
Здесь, как обычно, ![]()
Вклад j-го сферического источника можно представить в виде гармонического ряда Фурье на интервале (![]() , L):
, L):
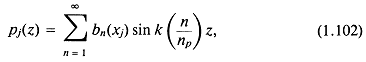
где ![]() — ширина импульса в направлении n в единицах полуволн
— ширина импульса в направлении n в единицах полуволн ![]()
Коэффициенты ![]() , входящие в уравнение (1.102), согласно теории преобразования Фурье, имеют вид
, входящие в уравнение (1.102), согласно теории преобразования Фурье, имеют вид
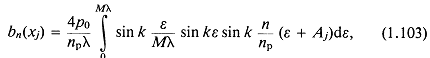
а интегрирование дает
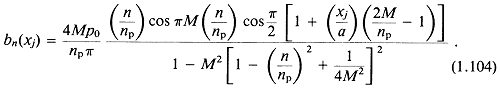
Все зависимости ![]() от апертуры, длины волны и угла заключены в параметре
от апертуры, длины волны и угла заключены в параметре ![]() — длине импульса в полуволнах.
— длине импульса в полуволнах.
Суммирование по всем элементам и изменение порядка суммирования дают
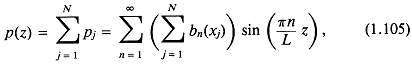
где
![]()
Азимутальная зависимость радиальной компоненты интенсивности ![]() (z) определяется выражением
(z) определяется выражением
![]()
Уравнение (1.107) в виде ряда Фурье имеет вид
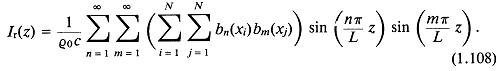
Радиальное сжатие информации в импульсе в направлении ![]() можно получить, усредняя радиальную компоненту интенсивности по всему импульсу:
можно получить, усредняя радиальную компоненту интенсивности по всему импульсу:
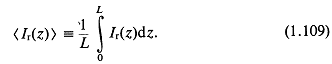
Для упрощения можно использовать свойство ортогональности 6-функции Кронекера (здесь это ![]() ):
):
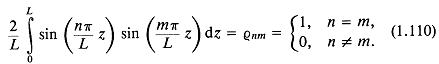
Параметр
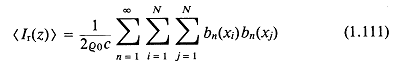
представляет собой удобную характеристику азимутальной структуры импульса.
Уравнения (1.104) и (1.111) — основной результат этого раздела. Их можно эффективно применять на малых компьютерах для расчета диаграммы направленности линейных решеток. Этот подход служит для иллюстрации аналитических методов, которые можно использовать совместно с решениями для простых источников, чтобы определить диаграммы направленности более сложных излучателей. Уравнения (1.104) и (1.111) являются исходными для оптимизации решетки, если требуется сканируемый точечный фокус.
1.5. РАСПРЕДЕЛЕННЫЕ ГАРМОНИЧЕСКИЕ ИСТОЧНИКИ И УГЛОВОЙ СПЕКТР ПЛОСКИХ ВОЛН
Для описания поля излучения (акустического или электромагнитного) широко применяется понятие диаграммы направленности, описываемой как функция какой-либо количественной характеристики поля в полярных координатах относительно некоторой фиксированной точки источника излучения. Однако, при более глубоком рассмотрении оказывается, что эта характеристика полностью описывает поле лишь на расстояниях от источника, много больших его размеров и длины волны в среде. В медицинских ультразвуковых приборах зачастую важно не накладывать таких ограничений, и необходим более универсальный подход. Это возможно, если принять [4], что любое произвольное акустическое (или электромагнитное) возмущение на плоской апертуре порождает в полупространстве излучения бесконечное множество плоских волн, направления распространения которых заполняют телесный угол 27г, а амплитуды и фазы этих волн, зависящие от направления их распространения, образуют так называемый «угловой спектр плоских волн». В выборе плоских волн нет ничего особенного с физической точки зрения —это результат выбора декартовой системы координат для написания основных уравнений. Другие (криволинейные) системы координат привели бы к другим формам элементарных волн.
Для наших целей важны два свойства такого формализма. Во-первых, преодолевается ограничение, налагаемое при использовании диаграммы направленности в полярной системе координат, а именно определение одной из точек как центра источника излучения. Во-вторых, угловой спектр представляется как преобразование Фурье начального распределения возмущения по апертуре. Последнее свойство, имеющее очевидную практическую ценность для вычислений, применимо к диаграмме в полярных координатах лишь в приближенном и ограниченном смысле.
В этом разделе, следуя в основном работам [14, 32], будут выведены уравнения, описывающие непрерывное излучение распределенного источника в безграничное полупространство. Будут рассмотрены круглый и прямоугольный поршневые излучатели, расположенные в плоскости экрана. Для определения углового спектра плоской волны будет использовано преобразование Фурье. В процессе вывода станет очевидна роль этих спектров в получении пространственных распределений давления и скорости частиц.
Амплитуда и угловая плотность плоских волн в спектре зависят от геометрии источника и амплитуды его возбуждения. Характеристика направленности в дальнем поле источника связана с амплитудным распределением по его апертуре таким же образом, как непрерывный спектр связан с конечным временным рядом.
1.5.1. ОПРЕДЕЛЕНИЕ УГЛОВОГО СПЕКТРА ПЛОСКИХ ВОЛН
Начнем с повторения определений: ![]() . Относительно потенциала скорости
. Относительно потенциала скорости ![]() записывается система уравнений, которая может быть разрешена относительно давления р и скорости частиц v:
записывается система уравнений, которая может быть разрешена относительно давления р и скорости частиц v:
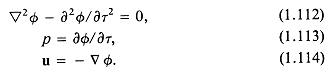
Если ![]() — акустически активная часть плоской границы R полупространства, a z — направление, нормальное к этой границе, то физическая интуиция подсказывает следующие граничные условия для акустически пассивной части R (т. е. R -
— акустически активная часть плоской границы R полупространства, a z — направление, нормальное к этой границе, то физическая интуиция подсказывает следующие граничные условия для акустически пассивной части R (т. е. R - ![]() ):
):
![]() (для абсолютно жесткой поверхности), (1.115)
(для абсолютно жесткой поверхности), (1.115)
![]() (для абсолютно мягкой поверхности). (1.116)
(для абсолютно мягкой поверхности). (1.116)
Эти условия можно записать для потенциала скорости в виде
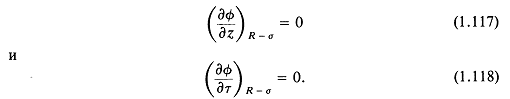
Кроме того, необходимо, чтобы потенциал ![]() был всюду конечным. Можно разделить переменные, полагая
был всюду конечным. Можно разделить переменные, полагая
![]()
Подстановка (1.119) в (1.112) после некоторых алгебраических преобразований дает
![]()
Каждый член в (1.120) зависит лишь от одной из независимых переменных х, у, z и ![]() ; следовательно, каждый член в отдельности есть постоянная.
; следовательно, каждый член в отдельности есть постоянная.
Например, рассмотрим член, зависящий от х. Если ![]() , то получаем периодическое решение для
, то получаем периодическое решение для
![]()
где А и В — постоянные интегрирования. Обобщение дает
![]()
Отсюда видно, что зависимость от одной из величин к можно исключить, используя (1.122):
![]()
В случае гармонических источников зависимость от времени выбирается в виде ![]() . Отметим, что при таком выборе
. Отметим, что при таком выборе ![]() . При этом путем подстановки убеждаемся, что
. При этом путем подстановки убеждаемся, что
![]()
Решение (1.124) имеет вид
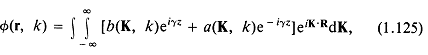
где ![]()
Из (1.125) можно получить выражения для компонент скорости частиц, например
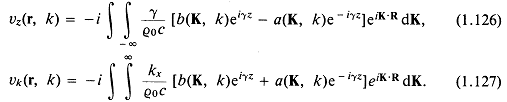
Чтобы продвинуться дальше, введем ![]() -функцию Дирака. Это облегчит работу с уравнениями (1.126) и (1.127). 5-функция Дирака является обобщенной и может быть представлена в одной из следующих форм:
-функцию Дирака. Это облегчит работу с уравнениями (1.126) и (1.127). 5-функция Дирака является обобщенной и может быть представлена в одной из следующих форм:
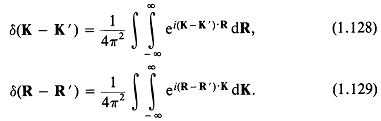
Следующее соотношение показывает свойство ![]() -функции, пригодное для обращения двумерных фурье-образов:
-функции, пригодное для обращения двумерных фурье-образов:
![]()
Здесь ![]() -функция используется для получения явных выражений для a(K, k) и b(K, k) из выражений для составляющих v(r, k).
-функция используется для получения явных выражений для a(K, k) и b(K, k) из выражений для составляющих v(r, k).
Обращение (1.126) и (1.127) с помощью (1.128) и (1.129) дает
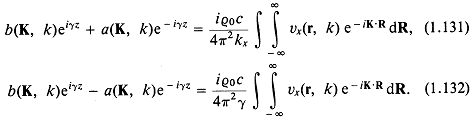
Складывая и вычитая эти уравнения, получаем
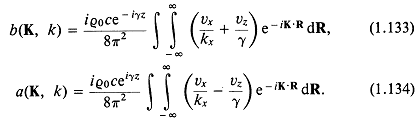
В отсутствие падающей волны ![]() . Это подтверждается отождествлением a(K, k) с плосковолновым спектром излучаемых волн. При этом
. Это подтверждается отождествлением a(K, k) с плосковолновым спектром излучаемых волн. При этом
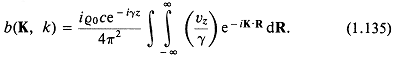
Если ![]() — акустически активная поверхность, a R —
— акустически активная поверхность, a R — ![]() есть ее дополнение до бесконечной плоской границы полупространства, то для абсолютно жесткой поверхности R -
есть ее дополнение до бесконечной плоской границы полупространства, то для абсолютно жесткой поверхности R - ![]()
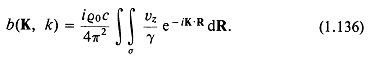
Для движения поршня на плоской поверхности с активной областью ![]() и жесткой областью R-
и жесткой областью R-![]() уравнение (1.136) преобразуется к виду
уравнение (1.136) преобразуется к виду
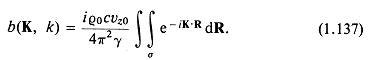
Очевидно, решение b(K, k) сводится к оценке интеграла в (1.137). Рассмотрим, например, акустически активную область с площадью 4ab:
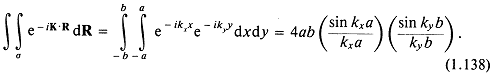
Этот результат для прямоугольного поршня можно преобразовать в выражение для круглого поршня следующей подстановкой:
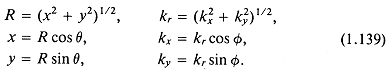
Следовательно, ![]() представляется в виде
представляется в виде
![]()
Прежде чем интегрировать по R и ![]() , необходимо определить множитель интегрирования, задаваемый якобианом
, необходимо определить множитель интегрирования, задаваемый якобианом
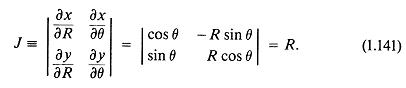
Для дифференциала площади теперь возможна следующая подстановка:
![]()
Следовательно, для круглого поршня
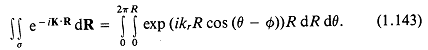
Так как
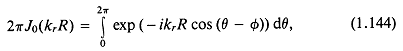
уравнение (1.143) сводится к
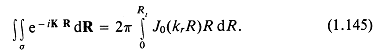
Существует и другое тождество:
![]()
Тогда из (1.145) и (1.146)
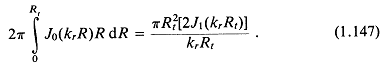
Таким образом, для плоских прямоугольного и круглого поршней в жестком плоском экране будет соответственно
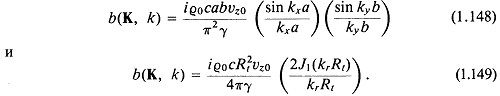
Итак, определены явные выражения для b(K, k), которые можно использовать для получения ![]() (
(![]() ), подстановкой в (1.125) с условием а(K, k) = 0.
), подстановкой в (1.125) с условием а(K, k) = 0.
Например, для прямоугольного поршня в бесконечном экране
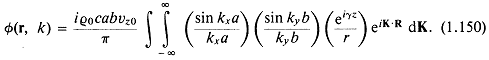
Для круглого поршня
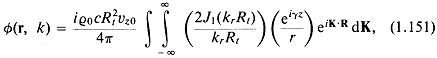
где ![]() .
.
Выражения для компонент скорости частиц естественно следуют из (1.126) и (1.127) при тех же условиях, при которых были получены (1.150) и (1.151). И наоборот, можно работать с уравнениями (1.150) и (1.151), используя (1.114) для получения ![]() , а также остальных составляющих скорости частиц.
, а также остальных составляющих скорости частиц.
1.5.2. СРЕДНЯЯ ПО ВРЕМЕНИ МОЩНОСТЬ ИЗЛУЧЕНИЯ РАСПРЕДЕЛЕННОГО ГАРМОНИЧЕСКОГО ИСТОЧНИКА
Полную мощность, проходящую через плоскую поверхность перпендикулярно ей, можно вычислить, интегрируя нормальную составляющую интенсивности по всей плоскости. В разд. 1.5.1 предполагалась зависимость от времени вида ![]() . При этом
. При этом
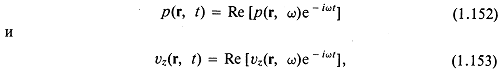
где ![]() — реальная часть произвольной комплексной функции. Полная мощность, излучаемая в полупространство, есть
— реальная часть произвольной комплексной функции. Полная мощность, излучаемая в полупространство, есть
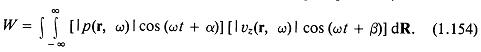
Если, как и раньше, для обозначения усреднения по времени использовать угловые скобки < >, то
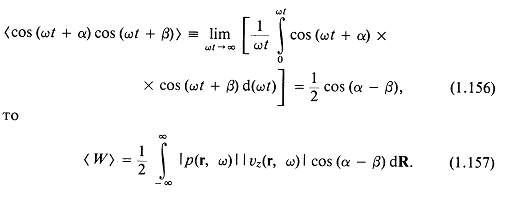
С другой стороны, можно ввести комплексное сопряжение, обозначив его звездочкой:
![]()
Тогда
![]()
Средняя по времени излученная мощность на частоте ![]()
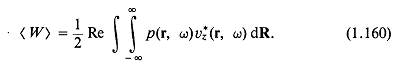
Если задать ![]() , то видно, что
, то видно, что
![]()
Из уравнения (1.125), где в отсутствие падающей волны а(К, /:) = 0, видно, что
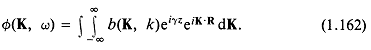
Следовательно,
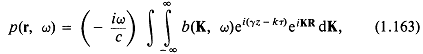
и из уравнения (1.126) при ![]() следует
следует
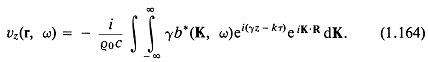
Затем, очевидно, надо подставить эти выражения в (1.160). При этом важно различать переменные интегрирования в выражениях для vz и р. Следовательно, необходимо в уравнении (1.164) заменить ![]() и K на
и K на ![]() ' и K'. Использование
' и K'. Использование ![]() -функции после подстановки в (1.160) показывает, что, согласно (1.158),
-функции после подстановки в (1.160) показывает, что, согласно (1.158),
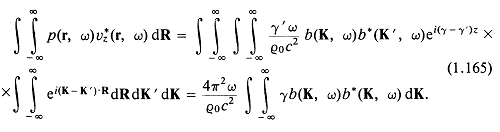
Итак, определены два различных выражения для средней по времени мощности излучения распределенного источника: одно — через скорость частиц и давление, другое — через угловой спектр плоских волн. Последнее имеет вид
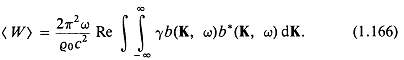
Здесь нас интересуют лишь волны, распространяющиеся в положительном z-направлении, следовательно, надо интегрировать лишь по той части плоскости, где ![]() — реальная величина. Тем самым мы избегаем появления нераспространяющихся или «пропадающих» волн и бесконечных пределов интегрирования.
— реальная величина. Тем самым мы избегаем появления нераспространяющихся или «пропадающих» волн и бесконечных пределов интегрирования.
В качестве упражнения читатель может самостоятельно подставить выражения (1.148) и (1.149) в (1.166).
1.5.3. СВЯЗЬ С ДИАГРАММОЙ НАПРАВЛЕННОСТИ В ДАЛЬНЕЙ ЗОНЕ
Между диаграммой направленности и угловым спектром плоских волн существует интересная связь [26]. Можно показать, что величина ![]() прямо пропорциональна нормированному давлению в дальней зоне в направлении z. Это будет выполнимо при
прямо пропорциональна нормированному давлению в дальней зоне в направлении z. Это будет выполнимо при ![]() , где А — характерный размер апертуры, например диаметр кругового поршня.
, где А — характерный размер апертуры, например диаметр кругового поршня.
Запишем эти соотношения
![]()
Здесь зависимость от z амплитуды и фазы комплексной функции давления устраняется множителем ![]() .
.
Давление в дальней зоне в определенном направлении можно связать с ![]() через углы, измеряемые от некоторого фиксированного отсчетного направления, так что вращением преобразователя вокруг оси, проходящей через его апертуру, относительно неподвижного измерительного датчика в дальнем поле можно измерить угловой спектр. Очевидно, что направление z, так же как и направление измерительного датчика, ничем не выделено.
через углы, измеряемые от некоторого фиксированного отсчетного направления, так что вращением преобразователя вокруг оси, проходящей через его апертуру, относительно неподвижного измерительного датчика в дальнем поле можно измерить угловой спектр. Очевидно, что направление z, так же как и направление измерительного датчика, ничем не выделено.
В работе [20] выполнена экспериментальная проверка уравнения (1.167) в ограниченном диапазоне углов. В этой работе не встретилось каких-либо серьезных проблем.
1.6. НЕСТАЦИОНАРНЫЕ ПОЛЯ ИЗЛУЧЕНИЯ РАСПРЕДЕЛЕННЫХ ИСТОЧНИКОВ
В разд. 1.3 и 1.4 рассматривались методы и примеры моделирования нестационарного излучения распределенных источников в том приближении, что излучатель состоит из простых источников, излучающих волны простой геометрии. В разд. 1.5 рассмотрены более строгие методы предсказания полей идеальных распределенных излучателей гармонических волн с временной зависимостью вида ![]() . При этом было введено понятие углового спектра плоской волны.
. При этом было введено понятие углового спектра плоской волны.
Теперь рассмотрим вкратце излучение импульса распределенным источником. Обсуждение конкретных задач потребовало бы нежелательно большой детализации с учетом множества форм импульсов и геометрических характеристик излучателей. Большая часть методов уже изложена в разд. 1.5.
Исследование импульсных полей распределенных источников требует лишь изменения зависимости от времени:
![]()
следовательно, импульс от распределенного источника можно описать выражением
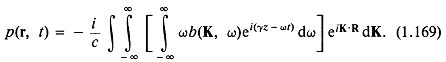
Отметим, что ![]() не зависит от выбора системы координат (r, t).
не зависит от выбора системы координат (r, t).
Понятие ![]() -функции Дирака можно обобщить на трехмерный случай, если рассматривать переменные (R, t) с одной стороны, и переменные
-функции Дирака можно обобщить на трехмерный случай, если рассматривать переменные (R, t) с одной стороны, и переменные ![]() — с другой. Эти системы представлены соответственно координатами
— с другой. Эти системы представлены соответственно координатами ![]() и k:
и k:
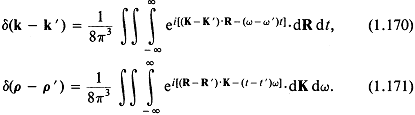
Умножим уравнение (1.169) на ![]() и проинтегрируем по Rиt:
и проинтегрируем по Rиt:
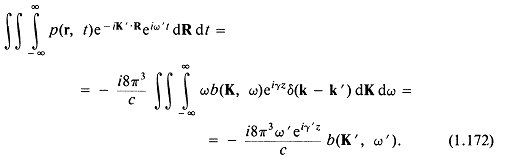
Уравнения (1.169) и (1.173) образуют искомую пару преобразований Фурье. Зная распределение давления во времени на заданной плоскости, можно с их помощью предсказать дальнейшее поведение импульса в пространстве.
Дополнительный материал по этой тематике можно найти, например, в работах [7, 11, 28]. Описание некоторых особенностей нестационарных полей приведено в разд. 2.3.
1.7. ОДНОМЕРНОЕ ВОЛНОВОЕ ДВИЖЕНИЕ
Во многих обзорах и учебниках как по общей, так и по медицинской акустике обсуждается распространение волн лишь в виде простого гармонического движения в плоской бегущей волне. Это, конечно, частный случай более общего трехмерного решения уже обсуждавшегося волнового уравнения, который имеет слабое отношение к медицинской акустике. Дело в том, что взаимодействие одномерных фронтов плоских волн с бесконечными плоскими границами раздела, конечно же, является плохой моделью распространения ультразвуковых импульсов в теле человека. Однако простота такой модели делает ее удобной для описания связи между акустической волной и средой, в которой она распространяется. Будет показано, что на практике одномерная модель также иногда допустима — при конструировании акустических систем.
1.7.1. СВЯЗЬ ПАРАМЕТРОВ АКУСТИЧЕСКОЙ ВОЛНЫ СО СВОЙСТВАМИ МАТЕРИАЛА
Из уравнения (1.38) мы знаем, что в случае плоской бегущей волны z-компонента мгновенного значения интенсивности связана с мгновенными возмущениями давления и скорости частиц:.
![]()
Можно показать, что соответствующие смещение и ускорение частиц среды представляются в виде
![]()
где ![]() ,
, ![]() — угловая частота акустического поля.
— угловая частота акустического поля.
Усредненная по одному или нескольким полным периодам гармонического колебания интенсивность
![]()
где V и Р — амплитуды скорости частиц и флуктуаций давления.
Этот сильно упрощенный анализ может пригодиться для получения соотношений между звуковым полем и некоторыми параметрами, с которыми оно связано. Эти параметры играют роль количественных характеристик взаимодействия поля и среды и могут быть измерены. Реальные значения некоторых параметров при обычных условиях приведены в табл. 1.1.

Интересной особенностью уравнений акустического поля в одномерной записи является их очевидное формальное тождество с телеграфными уравнениями для электрических линий передачи (см., например, [9]). Практическая важность этого формального сходства состоит в том, что оно позволяет применять хорошо развитую теорию линий передачи для решения ряда задач акустики бегущих плоских волн. Соответствующие аналогии между электрическими и акустическими величинами сведены в табл. 1.2.
Таблица 1.2. Электрические и акустические аналоги
Эта аналогия показывает, что акустическая величина go с играет роль аналогичную характеристическому импедансу линии передачи. Поэтому будем называть эту величину характеристическим акустическим импедансом среды и обозначать ее символом Z. Однако при этих рассуждениях мы стараемся не замечать, что за исключением частного случая распространения плоских волн скорость частиц состоит из трех векторных компонент и что применение импеданса в форме ![]() неприемлемо. Полезна обратная величина, вектор v/p, обычно называемая акустической проводимостью.
неприемлемо. Полезна обратная величина, вектор v/p, обычно называемая акустической проводимостью.
Типичные значения ![]() , с и Z для некоторых веществ перечислены в табл. 1.3, но необходимо помнить, что биологические ткани— это «композитные» материалы, состоящие из различных компонент, в которых значения этих параметров могут существенно отличаться от значений для всей ткани.
, с и Z для некоторых веществ перечислены в табл. 1.3, но необходимо помнить, что биологические ткани— это «композитные» материалы, состоящие из различных компонент, в которых значения этих параметров могут существенно отличаться от значений для всей ткани.
Имеется настоятельная необходимость создания надежных и исчерпывающих таблиц основных акустических свойств неорганических и биологических материалов, представляющих интерес для медицинской акустики. В настоящее время большая часть имеющих данных рассеяна по литературе; некоторые полезные таблицы приведены в работах [2, 13].
В разд. 1.7.2—1.7.4 перечислены некоторые простые, но практически важные результаты для одномерного волнового движения, определяемого одномерными уравнениями неразрывности и движения, эквивалентными уравнениям линии передачи (см., например, [9, 15]).
Таблица 1.3. Приближенные значения плотности, скорости звука и характеристического импеданса для некоторых веществ, существенных для медицинской акустики (при 37 °С)
|
Вещество |
Плотность |
Скорость звука с (м/с) |
Характеристический импеданс Z (Рл = кг-м-2 с-1) |
|
|
|
|
Х10-6 |
|
Вода |
993 |
1527 |
1,516 |
|
Четыреххлористый углерод |
1595 |
887 |
1,415 |
|
Этиловый спирт |
789 |
1119 |
0,883 |
|
Тетрабромэтан |
2693 |
1041 |
3,08 |
|
Печень |
1060 |
1560 |
1,65 |
|
Кровь |
1060 |
1530 |
1,62 |
|
Жир |
950 |
1450 |
1,38 |
|
Кость |
1200—1800 |
2700—4100 |
3,2—7,4 |
|
Полиэтилен |
920 |
2000 |
1,8 |
|
Полистирол |
1056 |
2350 |
2,48 |
|
Полиметилметакрилат |
1190 |
2680 |
3,2 |
|
Алюминий |
2700 |
6420 |
17,3 |
|
Сталь |
7900 |
5800 |
45,8 |
|
Воздух при нормальных условиях |
1,2 |
330 |
0,0004 |
1.7.2. ОТРАЖЕНИЕ И ПРОХОЖДЕНИЕ ПРИ НОРМАЛЬНОМ ПАДЕНИИ
Коэффициенты отражения R и прохождения Т по давлению для случая нормального падения плоской бегущей волны на плоскую границу раздела двух сред с импедансами Z1 и Z2 —
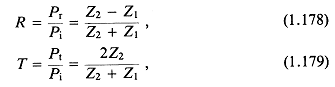
где P1, Pr и Pt —амплитуды давления падающей, отраженной и прошедшей волн.
Из (1.178) видно, что величина Pr/Pi может быть как положительной, так и отрицательной в зависимости от соотношения Z1 и Z2. Другими словами, отражение от границы, на которой характеристический импеданс уменьшается, приведет к изменению фазы отраженного сигнала: сжатие среды выразится в виде положительного избыточного давления и наоборот. Акустическое давление в прошедшей волне, напротив, всегда будет в фазе с падающей на границу волной (см. (1.179)).
Соответствующие выражения для коэффициентов отражения и прохождения по интенсивности имеют вид
где ![]() и
и ![]() — средние по времени интенсивности падающей, отраженной и прошедшей волн.
— средние по времени интенсивности падающей, отраженной и прошедшей волн.
Для фронта плоской волны, падающей под углом к плоскости раздела двух жидких сред (так что нормали к фронту и поверхности раздела образуют угол ![]() , а нормаль к поверхности раздела образует угол
, а нормаль к поверхности раздела образует угол ![]() с нормалью к фронту прошедшей волны), справедливы следующие выражения для коэффициентов отражения и прохождения по интенсивности:
с нормалью к фронту прошедшей волны), справедливы следующие выражения для коэффициентов отражения и прохождения по интенсивности:
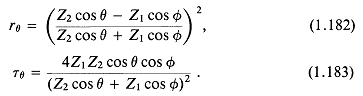
Кроме того, известен закон Снелля
![]()
где с1 с2 — значения скорости звука в первой и второй средах.
В частности, когда с2>с1, при условии ![]() существует критический угол «полного внутреннего отражения»:
существует критический угол «полного внутреннего отражения»:
![]()
Если один или оба материала твердые, а не жидкие, то при наклонном падении возникает возможность преобразования энергии продольных колебаний в поперечные (сдвиговые), и приведенные выражения не будут правильно описывать явление.
1.7.4. ПРОХОЖДЕНИЕ ЧЕРЕЗ ПЛАСТИНКУ (НОРМАЛЬНОЕ ПАДЕНИЕ)
В случае когда фронт плоской волны нормально падает на плоскопараллельный слой среды «2», разделяющий среды «1» и «3», коэффициент прохождения энергии в среду «3»:
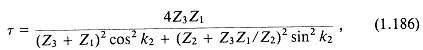
где ![]() —толщина слоя,
—толщина слоя, ![]() — длина звуковой волны в среде «2».
— длина звуковой волны в среде «2».
Можно рассмотреть это выражение в нескольких случаях, имеющих практическое значение.
В частном случае ![]() (тонкий слой газа на границе раздела) в знаменателе будет преобладать второй член, и коэффициент пропускания оказывается очень малым. Примером может служить плохо смоченный гидрофон (см. гл. 3), чувствительность которого может быть значительно сниженной.
(тонкий слой газа на границе раздела) в знаменателе будет преобладать второй член, и коэффициент пропускания оказывается очень малым. Примером может служить плохо смоченный гидрофон (см. гл. 3), чувствительность которого может быть значительно сниженной.
Выражение также упрощается при cosk2 = 1 или sink2 = 1. В первом случае ![]() , где n — целое число (или нуль), при этом
, где n — целое число (или нуль), при этом
![]()
и прохождение через такой «полуволновой» слой не зависит от его материала.
В другом случае, когда ![]()
![]()
Отсюда, выбирая ![]() , можно получить
, можно получить ![]() =1, т. е. полное прохождение через «четвертьволновую пластинку», которая служит трансформатором импеданса. Это важно при оптимизации акустического контакта между твердым материалом преобразователя и жидкой средой (см., например, гл. 2), хотя, как будет отмечено, такое устройство очень избирательно по частоте.
=1, т. е. полное прохождение через «четвертьволновую пластинку», которая служит трансформатором импеданса. Это важно при оптимизации акустического контакта между твердым материалом преобразователя и жидкой средой (см., например, гл. 2), хотя, как будет отмечено, такое устройство очень избирательно по частоте.
Выражения для коэффициента прохождения через слой при наклонном падении крайне сложны, поскольку в общем случае по крайней мере одна из сред является твердой, что влечет за собой преобразование продольной моды в поперечную.
1.8. НЕЛИНЕЙНЫЕ ЭФФЕКТЫ В ЖИДКИХ СРЕДАХ БЕЗ ПОТЕРЬ
В этом разделе приводится краткий вывод соотношений, необходимых для описания эффектов нелинейной акустики в жидкостях без потерь. Более полное исследование выполнено в работе Блекс-тока [3]. В разд. 1.2 этой главы были выведены основанные на линейной акустической теории соотношения между такими величинами, как интенсивность и плотность энергии, которые мы будем называть квадратичными величинами. В этом разделе этим величинам будет дано более серьезное обоснование и будут представлены новые соотношения, не следующие непосредственно из линейной теории.
Хороший пример одного из таких соотношений — выражение для силы, действующей на объект, помещенный в акустическое поле. Применение этого выражения для «радиационного давления» будет обсуждаться в гл. 3.
Приведенные ниже уравнения — это второй закон Ньютона и закон сохранения энергии для механики сплошной среды без потерь:
![]() (сохранение импульса); (1.189)
(сохранение импульса); (1.189)
![]()
![]() (сохранение энергии); (1.191)
(сохранение энергии); (1.191)
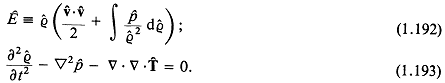
«Крышка» над зависимыми переменными введена, чтобы избежать сложных обозначений при разделении величин на постоянные и зависящие от пространства и времени. Такими зависимыми переменными являются давление р, плотность ![]() и скорость частиц v.
и скорость частиц v. ![]() — тензор 2-го ранга, например
— тензор 2-го ранга, например ![]() —полная энергия в единице объема (плотность энергии). Независимой переменной является t.
—полная энергия в единице объема (плотность энергии). Независимой переменной является t.
Уравнение (1.193) представляет собой обобщенное «волновое уравнение», которое может быть получено из выражений (1.189) и (1.191).
Уравнения (1.189) и (1.191) образуют нелинейную систему, которая следовательно, не может быть легко решена без учета взаимодействий При работе с этими уравнениями можно начать с линеаризованных уравнений и определить внешние параметры р0 и ![]() - давление и плотность в отсутствие акустических или неакустических движений жидкости. Тогда
- давление и плотность в отсутствие акустических или неакустических движений жидкости. Тогда ![]() и
и ![]() можно записать в виде
можно записать в виде

где p, ![]() и v — акустические величины.
и v — акустические величины.
Уравнения (1.189) и (1.191) не образуют полную систему уравнений гидродинамики. Необходима дополнительная связь между флуктуациями давления и плотности:
![]()
Параметр В/А обычно называют параметром нелинейности. Он расширяет общее линейное выражение, полученное при В/А=0, до следующего порядка малости. При атмосферном давлении В/А зависит от типа жидкости, а для данной жидкости от температуры.
Если выразить уравнения (1.189) и (1.193) через v и р/p0 (путем применения (1.194) и (1.195)), то достаточно просто можно записать выражения 1-го и 2-го порядков. Например, уравнения 1-го порядка имеют вид
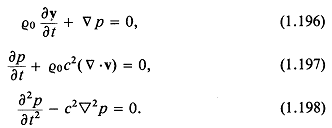
Здесь представлены члены, содержащие лишь одиночную независимую переменную, а не произведения двух и более
Обозначая усреднение по времени скобками < > и действуя на (1.189), получаем
![]()
где с точностью до 2-го порядка
![]()
Отметим, что производная по времени в уравнении (1.189) при усреднении дает нуль.
Уравнение (1.199) можно модифицировать с помощью соотношений 1-го порядка (1.196) и (1.197) и тождества
![]()
откуда следует
![]()
Из (1.202) непосредственно следует, что
![]()
где
![]()
Второе соотношение, содержащее средние по времени величины 2-го порядка, можно вывести из (1.196) и (1.197) или из (1.199) и (1.203):
![]()
По теореме Гаусса и связанному с ней интегральному тождеству
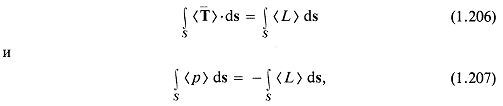
где S — поверхность объема жидкости, не содержащего источников, ds — дифференциальный элемент площади, направленный по единичному вектору нормали. Дополнительное соотношение 2-го порядка следует из (1.191):
![]()
или, по теореме Гаусса,
![]()
Значение уравнения (1.209) становится ясно, если рассмотреть «пучок» направленного преобразователя. Из этого выражения следует, что средняя по времени мощность, входящая в область без источников и стоков, равна по модулю излучаемой, если среднюю по времени интенсивность проинтегрировать по всему падающему и переизлученному пучку. Иными словами, мощность не увеличивается и не теряется внутри объема, а переизлучается.
Рассматривая радиационную силу, действующую на тело, необходимо иметь в виду, что величины в лагранжевых (движущихся) координатах связаны с величинами в эйлеровых (неподвижных) координатах соотношениями
![]()
где индекс «В» обозначает величину на движущейся границе объекта в системе координат, движущейся вместе с границей и смещенной на расстояние d.
Радиационная сила имеет вид
![]()
где ds — направление внешней нормали к поверхности тела. Из уравнения (1.196) видно, что
![]()
С точностью до второго порядка малости ![]() , поэтому
, поэтому
![]()
и, следовательно, из (1.204), (1.210), (1.211) и (1.212) можно получить следующее тождество:
![]()
или в упрощенном виде
![]()
Таким образом, интегрирование средней по времени плотности энергии по поверхности в направлении внутренней нормали к поверхности дает результирующую радиационную силу, действующую на объект. Использование уравнения (1.216) для получения более частного и полезного выражения для радиационной силы будет рассмотрено в гл. 3. Теоретические основы явления радиационного давления были предметом дискуссии: имеются две основополагающие статьи Вестервельта [30, 31] и полезный обзор Ливетта с соавт. [17].
21. Morse, P. M. & Ingard, К. Н. (1968) Theoretical acoustics, McGraw-Hill, New York
ГЕНЕРАЦИЯ АКУСТИЧЕСКИХ ПОЛЕЙ И ИХ СТРУКТУРА
К. Хилл
Широкое практическое использование ультразвука в медицине в значительной степени обусловлено возможностью создавать направленные ультразвуковые поля или пучки — другими словами, специфическими свойствами ультразвука как вида излучения. В данной главе рассматриваются практические методы генерации направленных акустических полей. Кроме того, проводится анализ характеристик реальных полей, которые можно создать с помощью этих методов и которые вместе с тем могут быть рассчитаны или смоделированы на основе аналитических результатов, представленных в гл. 1.
На данном этапе целесообразно провести некоторое уточнение самого понятия акустического поля. В медицинской акустике, как и в других областях акустики, практический интерес к направленным полям вызван, с одной стороны, возможностью избирательного воздействия на заданный участок биологической ткани или другой среды, а с другой стороны, возможностью селективного приема сигналов от ограниченной области пространства. На рис. 2.1 схематически изображена наиболее общая ситуация, анализ которой показывает, что целесообразно провести различие между тремя понятиями акустического поля:
1) поле излучения — пространственно-временное распределение акустического поля, создаваемого за счет излучения энергии некоторым конкретным устройством, называемым излучателем;
2) поле приема — пространственно-временное распределение фазовой и амплитудной чувствительности некоторого другого устройства, называемого приемником;
3) поле излучения-приема — пространственно-временное распределение фазовой и амплитудной чувствительности при наличии в среде точечной мишени, локализованной в области пересечения заданных полей излучения и приема.
Далее будет показано, что рассмотренная общая ситуация упрощается в весьма важном случае эхо-импульсных диагностических систем, когда характеристики излучателя и приемника в первом приближении можно считать одинаковыми.
Рис. 2.1. Три различных понятия акустического поля: ПИ — поле излучения, ПП — поле приема и ПИП — поле излучения-приема (И — излучатель, П — приемник, ЛРИ-6 — линия равной интенсивности излучения по уровню 6 дБ, ЛРЧ-6 — линия равной чувствительности приемника по уровню 6 дБ, ЛРИ-12 — линия равной интенсивности эхо-сигналов по уровню 12 дБ).
Однако из дальнейшего изложения станет также понятным, что учет более общего случая позволяет вскрыть некоторые интересные с практической точки зрения возможности и поэтому проведенная выше классификация представляется целесообразной.
Принятые выше определения подразумевают, что понятие об акустических полях значительно шире, чем представление о поле, созданном только при генерации акустических волн. В связи с этим четкое разграничение между данной главой и следующей, в которой будут рассмотрены конкретные вопросы регистрации акустических полей, становится достаточно условным.
При анализе физических методов, обеспечивающих генерацию акустических полей, мы рассмотрим в практическом плане только явление пьезоэлектричества. Однако для полноты представления необходимо отметить, что существуют и другие способы возбуждения акустических волн в ультразвуковом диапазоне частот. В частности, для генерации мощного ультразвука в частотном диапазоне 20—100 кГц обычно используются магнитострикционные преобразователи. Отметим, что в этом частотном диапазоне работают устройства ультразвуковой очистки, дезинтеграторы биологических клеток и целый ряд ультразвуковых хирургических инструментов.
В работе [4] проведен подробный теоретический анализ явления магнитострикции, а некоторые применения магнитострикционного эффекта рассмотрены в работе [27].
2.2. Пьезоэлектрические преобразователи
Пьезоэлектрический эффект представляет собой явление, которое наблюдается в образцах некоторых анизотропных материалов и заключается в нарушении равновесного распределения электрических зарядов под действием механической деформации образца. Возможен и обратный пьезоэлектрический эффект, состоящий в механической деформации среды под действием внешнего электрического поля. Явление пьезоэлектричества подробно рассмотрено в ряде специальных публикаций [3, 4, 6, 13].
Пьезоэлектрическим эффектом обладают материалы различного типа. К одному из классов таких материалов относятся естественные кристаллы и кристаллические материалы (к ним относятся также кости человека), причем наиболее важными с точки зрения практического применения являются кварц и ниобат лития. Другой важный класс объединяет сегнетоэлектрики — аморфные материалы типа некоторых керамик и пластмасс, имеющих микрокристаллическую структуру. В этих материалах устойчивый пьезоэлектрический эффект может быть создан под действием сильного электрического поля (такой процесс называется поляризацией).
Достаточно сложно дать исчерпывающую характеристику электромеханических свойств таких материалов. По своей природе они являются анизотропными, т. е. их свойства зависят от выбранного направления относительно кристаллографических осей или осей поляризации. При этом для описания взаимосвязи между различными электрическими и механическими характеристиками пьезоэлектриков необходимо использовать тензорно-матричные уравнения. К основным параметрам, характеризующим свойства различных материалов, следует отнести: коэффициент электромеханической связи, определяющий ту часть электрической энергии, которая может быть преобразована в упругую энергию и наоборот; пьезоэлектрический модуль, представляющий собой отношение наведенного электрического поля к единичной деформации и наоборот; диэлектрическую проницаемость; тангенс утла диэлектрических потерь — частотно-зависимую величину, определяющую ту часть энергии, которая теряется за период колебаний; плотность, упругую податливость и удельный акустический импеданс. В практическом плане важную роль играют также напряженность электрического поля пробоя, временная и температурная стабильность параметров, а также устойчивость к воздействию воды и химических веществ.
Значения перечисленных параметров для некоторых практически важных материалов представлены в табл. 2.1. С учетом того что в подавляющем большинстве медицинских и биологических приложений пьезоэлектрические преобразователи работают в режиме возбуждения только продольной моды колебаний (по толщине), в таблице приведены значения соответствующих параметров, относящиеся лишь к этой моде. Однако нельзя пренебрегать возможностью возбуждения и других мод колебаний, а также взаимодействием между различными модами. В дальнейшем мы еще вернемся к этому вопросу.
Как видно из табл. 2.1, между указанными материалами существуют некоторые важные с точки зрения практики различия. Так, например, кварц, относящийся к естественным кристаллическим материалам, характеризуется очень низкими потерями и, следователь но, обладает резко выраженными резонансными свойствами.
Таблица 2.1. Основные характеристики некоторых пьезоэлектрических материалов
|
|
Кварц |
Цирконаттитанат свинца |
Метаниобат свинца |
Поливинилиден- фторид | |
|
|
Х-среза |
PZT-4 |
PZT-5A |
|
(ПВДФ) |
|
Диэлектрическая проницаемость |
5,0 |
1300 |
1700 |
22,5 |
|
|
Коэффициент электромеханической связи при продольном пьезоэффекте |
0,1 |
0,7 |
0,7 |
0,38 |
0,19 |
|
Пьезоэлектрический модуль |
2 |
290 |
370 |
85 |
|
|
Тангенс угла диэлектрических потерь |
~10-4 |
0,004 |
0,02 |
0,01 |
|
|
Удельный акустический импеданс (относительно воды) |
7,6 |
14,7 |
13,6 |
10,3 |
1,5 |
Пластинки кварца помимо своей основной частоты могут с достаточно высокой эффективностью работать на целом ряде своих высших гармоник как в качестве излучателей, так и приемников ультразвука. С другой стороны, из-за низкого значения коэффициента электромеханической связи для кварцевых пластинок характерна сравнительно слабая чувствительность вне резонанса. Поэтому они непригодны для работы в широкой полосе частот или для использования в качестве приемников сигналов в тех случаях, когда отсутствует строгий контроль за частотой. В силу указанных причин кварц с его чрезвычайно высокой стабильностью параметров используется для измерения акустических характеристик материалов на различных фиксированных частотах. Он применяется, например, для точных измерений коэффициента поглощения и скорости звука в растворах биомолекул, для оценки соотношений между дозой ультразвука и биологическим эффектом. Однако кварц, вообще говоря, непригоден для использования в диагностике или дозиметрии.
Сегнетокерамические материалы типа цирконаттитаната свинца имеют сравнительно высокий коэффициент электромеханической связи и обладают заметной чувствительностью вне резонанса, что позволяет их использовать для работы в широкополосном режиме. С учетом высокой диэлектрической проницаемости из этих материалов могут быть изготовлены преобразователи достаточно малых размеров, электрический импеданс которых не будет чрезмерно большим. Значения коэффициента электромеханической связи сегнетоэлектриков обычно почти на порядок превосходят соответствующие значения для кварца. Поэтому сегнетокерамические материалы стали широко применяться для генерации и приема акустических волн в медицинских приложениях.
Устойчивый пьезоэлектрический эффект может быть также получен в некоторых синтетических полимерах посредством их поляризации в сильных постоянных электрических полях при повышенных температурах. Среди этих материалов наиболее перспективным представляется поливинилиденфторид (ПВДФ) [21, 30]. Хотя он обладает несколько более низким коэффициентом электромеханической связи и значительно меньшей по сравнению с цирконат-титанатом свинца диэлектрической проницаемостью, его удельный акустический импеданс близок к импедансу воды и мягких тканей, а его очень низкая механическая добротность Q обеспечивает возможность работы в широкой полосе частот. Кроме того, технологически его можно изготовить в виде тонкой гибкой пленки, что имеет большое практическое значение в ряде приложений.
Рис. 2.2. Основные элементы плоского круглого преобразователя
Сегнетоэлектрические материалы можно резать, придавать им необходимую форму и компоновать самым различным образом. Это позволяет создавать весьма универсальные и эффективные устройства генерации акустических полей. Некоторые из этих устройств будут рассмотрены в дальнейшем, а на первом этапе мы исследуем характеристики одной из простейших, но в то же время основных конструкций. Речь идет о преобразователе, рабочий элемент которого выполнен в форме плоского диска радиуса а с параллельными поверхностями. Типичная конструкция такого преобразователя показана на рис. 2.2.
В данном случае диск расположен на плоской границе раздела между двумя полубесконечными средами, одной из которых может быть вода или биологическая ткань, а другая представляет собой изолирующую среду, которой обычно является воздух. Математический анализ такого круглого поршневого излучателя уже был выполнен в гл. 1 (разд. 1.5.1).
При сборке преобразователя необходимо обеспечить механическое крепление диска, причем способ этого крепления в существенной степени определяется конкретным назначением устройства. При излучении и приеме непрерывных волн или «тональных» импульсов большой длительности на заданной частоте преобразова тель должен обладать высокой добротностью. Для ее обеспечения диск закрепляется только в периферийной области и с тыльной стороны «нагружается на воздух». При излучении и приеме коротких (широкополосных) импульсов желательно, чтобы преобразователь имел приблизительно равномерную частотную характеристику. С этой целью можно задемпфировать колебания диска при резонансе посредством его соединения с тыльной нагрузкой, которая в идеальном случае должна быть согласована с преобразователем по акустическому импедансу. Осуществить такое соединение можно, например, с помощью заливки из эпоксидной смолы. Обычно в качестве демпфера используется эпоксидная смола с наполнителем из вольфрамового порошка, а в случае пьезокерамических дисков им может служить элемент из той же самой, но неполяризованной керамики.
В дальнейшем будет показано, что материал тыльной нагрузки должен обладать заметным поглощением акустической энергии, с тем, чтобы предотвратить рассеяние или отражение (особенно когерентное) возбуждаемых в тыльной нагрузке волн в обратном направлении к диску. По этой причине форма и композиционный состав тыльной нагрузки должны быть тщательно подобраны.
Одна из трудностей, возникающих при использовании пьезоэлектрических керамических материалов, связана с высокими значениями их удельного акустического импеданса по отношению к воде (табл. 2.1). Различие импедансов приводит к плохому акустическому согласованию между преобразователем и рабочей средой. Так, например, в гл. 1 было показано, что при отношении импедансов, равном 14, потери энергии при двустороннем излучении определяются коэффициентом 0,062, т. е. составляют 12 дБ. Обычно для преодоления этих трудностей на поверхность преобразователя наносят один или два четвертьволновых согласующих слоя (см. разд. 1.7.4). Такой согласующий слой обеспечивает также механическую защиту электродов преобразователя и изготавливается из материала, обладающего хорошей смачиваемостью для предотвращения возможности образования воздушной прослойки на поверхности (разд. 1.7.4).
Помимо указанных выше требований к акустическому демпферу при разработке конструкции корпуса преобразователя необходимо учитывать и целый ряд других специфических моментов. Необходимо, чтобы подводящие электрические провода и электроды могли пропускать большие мгновенные токи. При этом важно обеспечить надежность контактов, что достигается обычно с помощью низкотемпературной пайки. Изоляция должна выдерживать высокие электрические напряжения и должна быть непроницаемой для воды. Преобразователи, предназначенные для работы в эхо-импульсном режиме или режиме приема, должны быть надежно экранированы, поскольку довольно часто возникает задача приема и выделения на фоне шумов акустических сигналов с мощностью порядка 10"12 Вт. Если для электрической экранировки используются металлические корпуса, то они должны быть очень хорошо акустически развязаны с рабочим элементом преобразователя. В противном случае эти корпуса будут работать как достаточно эффективные акустические линии задержки. Подробное рассмотрение метода оптимизации конструкций эхо-импульсных преобразователей выполнено в работе [32].
Обычно при теоретическом рассмотрении предполагается, что преобразователи, сконструированные в соответствии с указанными выше требованиями, будут совершать колебания подобно простому поршню, т. е. с одинаковой колебательной скоростью по всей площади поверхности рабочего элемента преобразователя. Однако такая модель является слишком упрощенной по крайней мере по двум причинам. Во-первых, некоторая часть акустической энергии будет расходоваться на возбуждение радиальных и изгибных мод колебаний, а во-вторых, при том или ином способе механического крепления рабочего элемента он может оказаться зажатым в периферийной области. Последний эффект, представляющий собой некоторую разновидность аподизации или маскирования, может играть и положительную роль, поскольку, как будет показано в дальнейшем, он приводит к уменьшению доли энергии, приходящейся в пространственной структуре пучка на боковые лепестки. Нередко также наблюдается, что дефекты, возникающие в процессе изготовления (например, при нарушении адгезии излучателя с тыльной нагрузкой или согласующим слоем), могут быть причиной явно выраженного аномального поведения преобразователя. Тем не менее теорию «простого поршневого преобразователя» можно рассматривать как неплохое первое приближение к поведению реальных устройств.
Второе основное упрощение большинства простых теоретических моделей сводится к предположению о непрерывном режиме возбуждения волн. Несмотря на такую идеализацию (см. далее разд. 2.3), соответствующие теоретические расчеты дают весьма наглядные результаты, которые непосредственно применимы на практике для описания ультразвуковых полей терапевтических или доплеровских диагностических аппаратов. Некоторые примеры расчета поля, создаваемого круглым поршневым излучателем в режиме непрерывного возбуждения, представлены на рис.
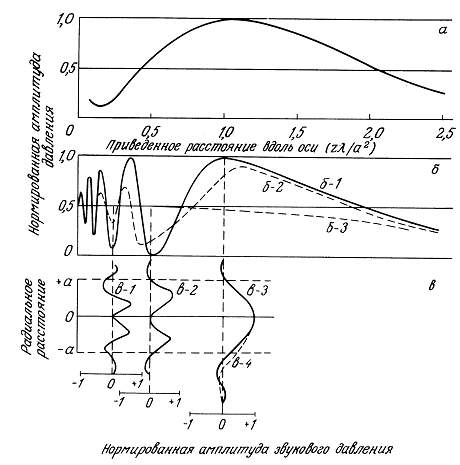
Рис. 2.3. Расчетные структуры полей плоских поршневых излучателей: а —нормированное распределение амплитуды звукового давления вдоль оси круглого излучателя радиуса а в случае равномерного возбуждения ![]() — то же для круглого излучателя с
— то же для круглого излучателя с ![]() — то же для излучателя квадратной формы со стороной
— то же для излучателя квадратной формы со стороной ![]() в случае
в случае ![]() — то же для круглого излучателя с
— то же для круглого излучателя с ![]() при использовании аподизирующей функции Гаусса; в — распределения амплитуды давления в радиальном направлении при фиксированных расстояниях по оси (кривые в-1, в-2 и в-3 соответствуют кривой б-1, кривая в-4 демонстрирует влияния аподизации).
при использовании аподизирующей функции Гаусса; в — распределения амплитуды давления в радиальном направлении при фиксированных расстояниях по оси (кривые в-1, в-2 и в-3 соответствуют кривой б-1, кривая в-4 демонстрирует влияния аподизации).
Как видно, по мере роста апертуры излучателя, выраженной в длинах волн ![]() , наблюдается тенденция к увеличению направленности (но также и к возрастанию сложности структуры поля). Кроме того, на представленных графиках можно видеть границу (определяемую достаточно условно «френелевским расстоянием»
, наблюдается тенденция к увеличению направленности (но также и к возрастанию сложности структуры поля). Кроме того, на представленных графиках можно видеть границу (определяемую достаточно условно «френелевским расстоянием» ![]() между ближним полем или зоной дифракции Френеля со сложной структурой и дальним полем или зоной дифракции Фраунгофера, где структура пучка упрощается, а интенсивность начинает спадать обратно пропорционально квадрату расстояния по оси излучателя.
между ближним полем или зоной дифракции Френеля со сложной структурой и дальним полем или зоной дифракции Фраунгофера, где структура пучка упрощается, а интенсивность начинает спадать обратно пропорционально квадрату расстояния по оси излучателя.
Равномерное возбуждение плоского круглого излучателя по всей поверхности представляет собой частный, но достаточно важный случай. Вопрос о «фокусирующих» излучателях, т. е. об излучателях с определенным законом изменения фазы и амплитуды в пределах их апертуры, рассматривается в разд. 2.4. Для сравнения на рис. 2.3 показана также структура поля плоского излучателя квадратной формы.
2.3. Импульсные акустические поля
В тех приложениях, где используются короткие импульсы ультразвука (например, в эхо-импульсной диагностической аппаратуре), теория непрерывного возбуждения волн уже не в состоянии дать правильное описание истинной картины поля. Поэтому необходимо воспользоваться более общим рассмотрением.
При анализе импульсного режима можно использовать два различных теоретических подхода. Первый состоит в том, чтобы предварительно для конкретного излучателя получить математическое решение в приближении монохроматической непрерывной волны и затем применить это решение к заданному частотному спектру. Вторая возможность заключается в использовании импульсной характеристики (т. е. решения для импульса во временной, а не в частотной области), на основе которой импульсное поле, а также и поле непрерывной волны могут быть рассчитаны точно. Этот метод, предложенный в работах [28, 29] и кратко рассмотренный в разд. 1.6, оказался особенно полезным. Дальнейшее его изложение базируется на представлении, развитом в работе [8].
В рамках этого метода основная задача состоит в расчете акустического возмущения в произвольной точке поля х (рис. 2.4) при заданной временной зависимости нормальной компоненты колебательной скорости ![]() на поршневом излучателе с плоской поверхностью S. Следует отметить, что важным моментом в развитии теории явилось доказательство того, что мгновенное акустическое давление р(х, t) в точке х может быть представлено в виде комбинации двух независимых функций,
на поршневом излучателе с плоской поверхностью S. Следует отметить, что важным моментом в развитии теории явилось доказательство того, что мгновенное акустическое давление р(х, t) в точке х может быть представлено в виде комбинации двух независимых функций,
описывающих колебания излучателя и геометрические условия задачи, причем обе эти функции поддаются практической оценке. В явном виде этот результат можно представить в форме временной свертки
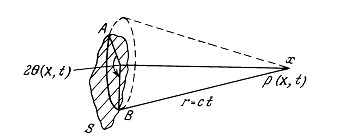
Рис. 2.4. Геометрические характеристики, используемые при анализе импульсного акустического поля [8].
![]()
где ![]() — плотность среды, а
— плотность среды, а ![]() — импульсная характеристика давления [35], представляющая собой функцию, которая связывает импульсное изменение скорости или смещения на поверхности излучателя с давлением поля в заданной локальной области.
— импульсная характеристика давления [35], представляющая собой функцию, которая связывает импульсное изменение скорости или смещения на поверхности излучателя с давлением поля в заданной локальной области.
Другой подход, который, по-видимому, является более точным, но менее пригодным с практической точки зрения, позволяет получить выражение для потенциала скорости в заданной точке поля х
![]()
где величина ![]() называется импульсной характеристикой потенциала скорости, причем упомянутая выше импульсная характеристика давления является первой производной по времени от этой величины.
называется импульсной характеристикой потенциала скорости, причем упомянутая выше импульсная характеристика давления является первой производной по времени от этой величины.
Практическая полезность представленных уравнений зависит от возможности оценки импульсной характеристики при конкретных конфигурациях излучателя. Методики такой оценки были рассмотрены для плоских круглых излучателей [28], для излучателей прямоугольной формы [17], а также для фокусирующих излучателей с вогнутой поверхностью [26]. Как видно из рис. 2.4, математически задача сводится к интегрированию по поверхности эквифазных элементов излучателя, задаваемых дугой AВ.
Следует отметить, что при определенных условиях метод импульсной характеристики может быть обобщен на случай, когда импульсный сигнал вновь попадает на источник в результате отражения от какой-либо точки среды или совокупности таких точек, представляющих собой протяженный рассеиватель или отражатель [35]. Такое обобщение достигается путем введения второго интеграла свертки.
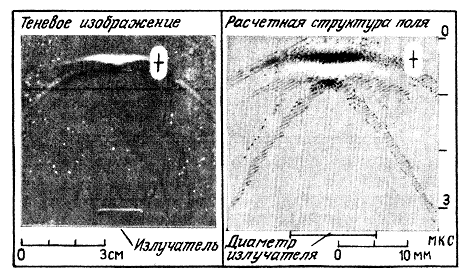
Рис. 2.5. Пространственная структура поля, создаваемого плоским круглым излучателем с ![]() на расстоянии 75
на расстоянии 75![]() от его поверхности в режиме возбуждения коротким импульсом. Слева показано изображение, полученное теневым методом, справа —расчетная структура. Теневое изображение представляет собой наблюдаемую глазом двумерную проекцию трехмерного поля, тогда как расчетная структура соответствует истинному сечению. Знаком + отмечена точка наблюдения, форма сигналов в которой показана на рис. 2.6, б [8].
от его поверхности в режиме возбуждения коротким импульсом. Слева показано изображение, полученное теневым методом, справа —расчетная структура. Теневое изображение представляет собой наблюдаемую глазом двумерную проекцию трехмерного поля, тогда как расчетная структура соответствует истинному сечению. Знаком + отмечена точка наблюдения, форма сигналов в которой показана на рис. 2.6, б [8].
Это дает возможность рассчитать форму сигналов, соответствующих полю излучения-приема в эхо-импульсном режиме. Подобная задача рассматривается в разд. 6.5.
Данный теоретический подход к расчету структуры импульсных акустических полей является весьма общим. В зависимости от конкретных условий теория будет приводить к самым разнообразным пространственным структурам акустического поля. Тем не менее один из важных общих выводов, хорошо согласующийся с экспериментом, заключается в том, что структура ближнего поля упрощается по сравнению с соответствующей картиной поля в случае непрерывного излучения (ср. рис. 2.3).
Рис. 2.5 иллюстрирует еще одну отличительную особенность импульсного поля. Здесь представлено сравнение расчетного поля круглого излучателя в фиксированный момент времени при импульсном возбуждении с соответствующей экспериментальной картиной поля, полученной теневым методом (см. гл. 3).
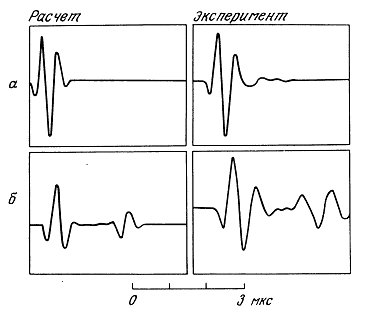
Рис. 2.6. Сравнение расчетной (слева) и измеренной (справа) формы сигналов в двух точках импульсного акустического поля плоского круглого излучателя с ![]() — координаты точки наблюдения на оси и в радиальном направлении) [8].
— координаты точки наблюдения на оси и в радиальном направлении) [8].
На рис. 2.6 представлено сравнение расчетной и измеренной временной формы импульса того же излучателя в заданной точке пространства, отмеченной крестиком на теневой картине рис. 2.5. Эти иллюстрации показывают, что по мере удаления от оси исходный импульс может трансформироваться в два (а иногда и более) раздельных импульса. Можно показать как на качественном уровне, так и аналитически, что эти импульсы соответствуют: а) плоской волне, которая распространяется в перпендикулярном к поверхности излучателя направлении и имеет неизменную амплитуду вплоть до бесконечности, и б) волне, излучаемой краем или периферией источника в противофазе с плоской волной. На рис. 2.7 (ср. рис. 2.5) отмечена траектория, вдоль которой волновой импульс распространяется от круглого излучателя. Показана плоская волна кругового сечения, за которой следует краевая или периферическая волна тороидальной формы. В общем случае во внутренних точках поля, т. е. в тех точках, которые лежат внутри объема, ограниченного апертурой излучателя, имеются три, а во внешних точках две составляющие, которые могут интерферировать друг с другом.
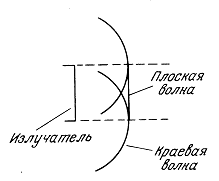
Рис. 2.7. Схематическое представление в осевом сечении импульсной плоской и краевой волн, создаваемых круглым поршневым излучателем [8].
Результат такой интерференции будет зависеть от их относительной пространственной локализации и длительности. Вторая и третья составляющие иногда называются «импульсными репликами» [10]. При использовании импульсного режима возбуждения в некоторых практических приложениях возникает необходимость в подавлении какой-либо из этих компонент поля. Для подавления краевой волны применяется аподизация (маскирование в радиальном направлении), а в качестве излучателей только краевой волны используются кольцевые преобразователи. Поле излучения-приема в случае дискового преобразователя состоит из трех, пяти или шести компонент.
До сих пор рассматривались акустические поля излучателей «плоских волн», т. е. таких излучателей, у которых фаза возбуждающего сигнала постоянна в пределах апертурной плоскости. Такие излучатели образуют особую группу и интерес к ним вызван достаточно тривиальными причинами. Во-первых, плоские преобразователи легко изготовить (отметим, что при изготовлении пьезоэлектрических преобразователей из кварца предварительно необходимо выделить заданную кристаллографическую плоскость). Во-вторых, теоретические результаты, полученные для плоских преобразователей, легче трактовать по сравнению со случаем искривленных поверхностей. Однако в общем случае поля оптимальной для практических приложений конфигурации отличаются от полей, создаваемых плоскими излучателями с равномерным возбуждением.
Целенаправленное отклонение от пространственной однородности либо функции возбуждения, либо функции отклика (либо их обеих вместе) в пределах апертуры преобразователя — аподизация — уже упоминалась как метод подавления краевых волн. В непрерывном режиме возбуждение краевых волн приводит к появлению паразитных боковых лепестков в структуре волнового пучка. Аподизация позволяет видоизменять структуру поля и в этом смысле может рассматриваться как метод обеспечения некоторой фокусировки. Такая возможность часто не учитывается при анализе методов фокусирования ультразвука. Естественно, что характер влияния аподизации источника на структуру поля будет зависеть от конкретного вида аподизирующей функции. Некоторые наглядные примеры этого представлены на рис. 2.3.
Более традиционным и более эффективным методом фокусирования является метод фазирования, состоящий во введении заданного закона распределения фазы возбуждающего сигнала в пределах апертуры излучателя. На практике такой метод реализуется с помощью различных способов. Прежде всего это достигается путем придания определенной формы активному элементу излучателя, например при использовании пьезокерамики или пьезопластических материалов. Второй способ состоит во введении соответствующих фазовых сдвигов между электрическими сигналами, подаваемыми на отдельные элементы многоэлементного преобразователя. Используются также акустические зеркала и линзы, которые, вообще говоря, дополнительно обеспечивают определенную степень аподизации за счет затухания в материале линзы. В дальнейшем будет показано, что между этими четырьмя способами существуют важные различия.
По аналогии с оптикой обычно принято считать, что сферическая поверхность является наиболее «естественной» формой фокусирующей поверхности. Однако не следует забывать, что широкое использование сферических преобразователей часто обусловлено простотой их изготовления, а вовсе не тем, что они во всех случаях имеют преимущества по сравнению с поверхностями другого профиля. Следует также отметить, что на практике многие фокусирующие системы характеризуются сравнительно небольшими значениями отношения диаметра излучателя к длине волны, при этом различие между «идеальной» и сферической поверхностями становится несущественным. Исключение составляют широкоугольные линзовые фокусирующие системы (типа тех, которые используются в акустических микроскопах, см. гл. 9), зеркальные системы, в которых применяются комбинации эллипсоидальных и гиперболоидных зеркал [22], а также аксиконовые системы, которые будут рассмотрены в разд. 2.4.2.
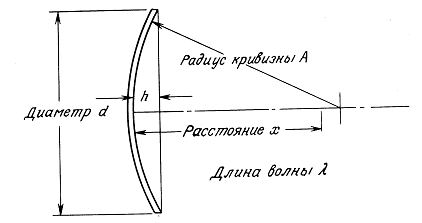
Рис. 2.8. Геометрические параметры, используемые при анализе фокусировки [15].
Следует отметить, что существуют разные (и неэквивалентные) определения фокуса акустического пучка. Так, например, согласно одному из них фокусом называется точка на оси, соответствующая минимальной ширине пучка. По другому определению фокус связывают с положением на оси максимума интенсивности акустического поля. Коссофф использовал последнее определение. На рис. 2.9 показаны полученные им результаты расчетов зависимости интенсивности от расстояния до излучателя вдоль оси для ряда преобразователей с различными степенями фокусировки. Интенсивность нормирована на максимальное значение интенсивности, создаваемой эквивалентным плоским преобразователем.
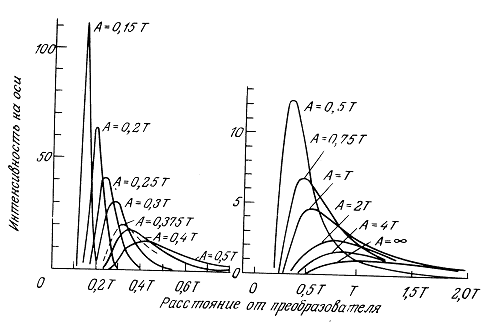
Рис. 2.9. Осевое распределение интенсивности в случае сферических фокусирующих преобразователей с различными коэффициентами эффективности ![]() . Здесь А — радиус кривизны преобразователя, а
. Здесь А — радиус кривизны преобразователя, а ![]() .
.
Из представленных данных непосредственно следует, что а) невозможно получить фокусировку в дальнем поле эквивалентного плоского преобразователя и б) акустический фокус всегда локализован в точке, сдвинутой относительно центра кривизны в сторону преобразователя, причем фокус будет приближаться к центру кривизны по мере возрастания степени фокусировки.
На фокусном расстоянии ширина ультразвукового пучка, определяемая интервалом между первыми минимумами распределения интенсивности в поперечном направлении, дается выражением (см. гл. 8)
![]()
Выигрыш в поперечной разрешающей способности при возрастании степени фокусировки или соответственно величины относи тельного отверстия 2а/r0 [1] неизбежно сопровождается потерей эффективной глубины фокусировки.
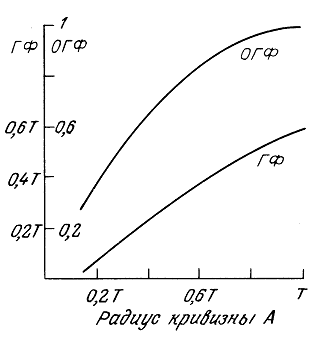
Рис. 2.10. Зависимость относительной глубины фокусировки (ОГФ) и глубины фокусировки (ГФ) от радиуса кривизны преобразователя круглого сечения [15].
Рис. 2.10 иллюстрирует как это происходит. Представленная здесь зависимость (необходимо отметить, что в данном случае результаты расчетов относятся к полю излучения, а не к полю излучения-приема) играет важную роль при разработке эхо-импульсных диагностических систем, когда в процессе конструирования необходимо принять компромиссное решение при выборе соотношения между поперечным разрешением и эффективной глубиной фокусировки системы. Этот вопрос обсуждается в гл. 8.
Следует отметить, что уравнение (2.5) дает точную оценку ширины пучка в фокальной плоскости только в случае некогерентного излучения. При наличии высокой пространственно-временной когерентности, которая имеет место почти во всех ультразвуковых полях, ширина пучка в фокусе будет, вообще говоря, возрастать. В работе [37] показано, что в предельном случае когерентных волновых цугов, протяженность которых превышает 103 длин волн, увеличение ширины пучка и соответствующее уменьшение разрешающей способности может достигать 2,5 раза.
Преобразование плоского волнового фронта в сходящийся можно осуществить с помощью акустической линзы. Обычно такая линза изготавливается из твердого материала, скорость распространения ультразвука в котором, как правило, превышает ее значения в водоподобных средах (иногда также используются жидкостные линзы, в которых жидкая среда заключена между двумя тонкими искривленными мембранами).
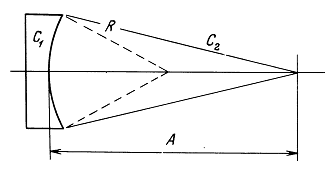
Рис. 2.11. Чертеж, поясняющий действие акустической линзы.
Поэтому твердотельные линзы имеют плосковогнутую форму (рис. 2.11). Если вогнутая поверхность линзы является сферической, то при малых относительных отверстиях преобразованный линзой волновой фронт также можно считать сферическим. В известной мере данный случай эквивалентен рассмотренному ранее случаю преобразователей со сферически-искривленными поверхностями, если эквивалентный радиус кривизны определяется в приближении геометрической акустики на основе закона Снелля по формуле
![]()
где ![]() — отношение скоростей звука в рабочей среде и материале линзы.
— отношение скоростей звука в рабочей среде и материале линзы.
В гл. 9 на примере сканирующих акустических микроскопов будет показано, что при заданном относительном отверстии линзы величина сферической аберрации будет снижаться при уменьшении ![]() . Этот вывод нетрудно понять из физических соображений, если учесть, что при все более высоких значениях Ci кривизна преобразованного линзой волнового фронта стремится к кривизне вогнутой сферической поверхности линзы (в работе [11] проведен более строгий анализ этого вопроса). К сожалению, требование малых значений
. Этот вывод нетрудно понять из физических соображений, если учесть, что при все более высоких значениях Ci кривизна преобразованного линзой волнового фронта стремится к кривизне вогнутой сферической поверхности линзы (в работе [11] проведен более строгий анализ этого вопроса). К сожалению, требование малых значений ![]() противоречит требованию отсутствия внутренних переотражений, т. е. критерию хорошего акустического согласования с рабочей средой. При высоких значениях Ci такое согласование могло бы быть обеспечено за счет соответственно малой плотности материала линзы, однако реальных материалов с требуемой комбинацией указанных параметров просто не существует. Отчасти эта проблема решается, если материал линзы обладает заметным затуханием звука. Однако высокое затухание приводит к возникновению новых проблем, связанных либо с потерей чувствительности в диагностических системах, либо с нагреванием и возможностью расплавления самой линзы при использовании мощного ультразвука. Как компромиссное решение, во многих практических приложениях для изготовления контактирующих с водой линз используется полистирол, обладающий поперечными связями между полимерными цепями. Иногда также применяется полиметилметакрилат, характеризующийся несколько более высоким значением скорости звука и значительно большим коэффициентом поглощения по сравнению с полистиролом. Подробный анализ возможностей фокусировки с помощью линз проведен в работах [2, 11, 14]. В работах [36] представлено сравнение полей импульсных акустических излучателей, имеющих различную форму и параметры фокусировки.
противоречит требованию отсутствия внутренних переотражений, т. е. критерию хорошего акустического согласования с рабочей средой. При высоких значениях Ci такое согласование могло бы быть обеспечено за счет соответственно малой плотности материала линзы, однако реальных материалов с требуемой комбинацией указанных параметров просто не существует. Отчасти эта проблема решается, если материал линзы обладает заметным затуханием звука. Однако высокое затухание приводит к возникновению новых проблем, связанных либо с потерей чувствительности в диагностических системах, либо с нагреванием и возможностью расплавления самой линзы при использовании мощного ультразвука. Как компромиссное решение, во многих практических приложениях для изготовления контактирующих с водой линз используется полистирол, обладающий поперечными связями между полимерными цепями. Иногда также применяется полиметилметакрилат, характеризующийся несколько более высоким значением скорости звука и значительно большим коэффициентом поглощения по сравнению с полистиролом. Подробный анализ возможностей фокусировки с помощью линз проведен в работах [2, 11, 14]. В работах [36] представлено сравнение полей импульсных акустических излучателей, имеющих различную форму и параметры фокусировки.
2.4.2. ПОЛЯ ПРЕОБРАЗОВАТЕЛЕЙ КРАЕВЫХ ВОЛН И АКСИКОНОВ
Формирование сферически сходящихся волновых фронтов не является единственным методом, обеспечивающим возможность получения остронаправленных акустических пучков с заданными параметрами. Как уже отмечалось, в одном из основных применений ультразвука, а именно в эхо-импульсной диагностике, в общем случае требуется, чтобы пучки имели достаточно равномерный узкий профиль на протяжении большой глубины фокусировки. На рис. 2.12 показан один из способов, позволяющих сформировать такие узконаправленные пучки.
Выделим тонкую полоску ВВ' на поверхности усеченного конуса АС. Если эта полоска действует как излучатель коротких импульсов, то она будет возбуждать волну тороидальной формы, краевые составляющие которой совпадают по фазе только в направлении вдоль оси конуса. Эхо-сигналы от оси можно зарегистрировать путем переключения данной полоски в режим приема. Поскольку подобное устройство имеет большое относительное отверстие в пределах определенного участка вдоль оси, сравнимого по своей протяженности с диаметром круговой полоски, то создаваемое им поле будет иметь центральный максимум, ширина которого в пределах этого участка сравнима с длиной волны. Свойства таких преобразователей «краевой волны» (см. разд. 2.3, посвященный импульсным полям) исследованы в работе [34]. К их недостаткам относится, по всей видимости, слабая чувствительность.
Рис. 2.12. Чертеж, поясняющий работу преобразователей краевых волн и аксиконов.
Рассмотрим теперь устройство, являющееся в некотором смысле обобщением предыдущей модели. Речь идет о преобразователе, рабочая поверхность которого охватывает всю поверхность АС усеченного конуса. Если такой преобразователь работает в режиме излучения (или приема или же приема-передачи), то его поле будет создаваться волновым фронтом, сходящимся от конуса АС (или расходящимся к нему). И вновь пространственная синфазность волн будет наблюдаться на оси, а временная синфазность — в той точке на оси конуса, для которой расстояние до оси вдоль нормали к конической поверхности (например, DO) соответствует времени распространения. Основательный анализ полей преобразователей такого типа проведен в работе [25]. По аналогии с оптикой данные устройства называются аксиконами. Разработаны также зеркальные аксиконы, в которых одно или несколько зеркал заданной формы используются в комбинации с плоским или искривленным преобразователем для генерации конического волнового фронта [5]. В разд. 2.6 рассматриваются характеристики одной из конкретных конструкций аксиконов. Показано, что с помощью аксиконов можно получить узкий центральный максимум в распределении поля (шириной порядка одной длины волны при больших значениях относительного отверстия) при сохранении значительной глубины фокусировки. Показано также, что по сравнению со сферическими фокусирующими системами аксиконные преобразователи (по крайней мере их простейшие конструкции) характеризуются более выраженными боковыми лепестками.
2.5. ФОРМИРОВАНИЕ ПУЧКОВ С ПОМОЩЬЮ РЕШЕТОК ПРЕОБРАЗОВАТЕЛЕЙ
До сих пор в данной главе обсуждались вопросы формирования ультразвуковых пучков при условии, что фаза возбуждающего сигнала (или чувствительность) одинакова по всей поверхности преобразователя. Изменение и регулировка фазовых соотношений в пределах активной поверхности преобразователя позволяют существенно расширить возможности таких устройств. Практически этого можно добиться, если разбить поверхность преобразователя на ряд отдельных элементов и ввести относительные фазовые сдвиги между электрическими сигналами, подаваемыми или снимаемыми с этих элементов. Используя соответствующий закон изменения фазы, можно в принципе сформировать волновой фронт любой требуемой формы. С помощью электронной коммутации фазовыми соотношениями можно управлять с очень высокой скоростью (характерное время переключения может составлять 10-6 с). Это позволяет с высоким быстродействием сканировать ультразвуковым пучком по пространству и получать динамическую фокусировку. Например, таким способом можно перемещать приемный фокус преобразователя вслед за волновым пакетом, излученным тем же самым преобразователем и удаляющимся от него со скоростью звука. В разд. 1.4.1 проведено предварительное ознакомление с теорией таких многоэлементных решеток.
Ранее рассматривались одноэлементные преобразователи, фокусирующие свойства которых обусловлены конфигурацией их поверхности или применением акустических линз. Фазированные решетки преобразователей являются более универсальными устройствами формирования пучков в том плане, что форма создаваемых ими волновых фронтов может отличаться от формы активных поверхностей используемых преобразователей (например, сферической или конической). Однако стоимость многоэлементных решеток достаточно высока. Кроме того, их характерной особенностью является дискретность требуемого фазового распределения в пределах волнового фронта. Такая дискретность обычно приводит к нежелательным искажениям структуры акустического поля, например к появлению «лепестков решетки». Тем не менее с учетом данной оговорки фазированные решетки преобразователей можно рассматривать как самостоятельный класс устройств для создания волновых фронтов, форма которых отличается от плоской. К таким устройствам применимы многие результаты анализа, проведенного ранее для одноэлементных фокусирующих систем.
Важное практическое значение имеют два основных типа решеток преобразователей — линейные и кольцевые решетки (рис. 2.13). Были предложены и преобразователи третьего типа, представляющие собой двумерную прямоугольную матрицу отдельных элементов. Однако такие преобразователи до сих пор не получили широкого применения, вероятно, вследствие высоких затрат на изготовление большого числа раздельных каналов излучения и приема.
Как показано на рис. 2.13, я, широко применяемые линейные решетки обычно изготавливаются в виде последовательности примыкающих друг к другу прямоугольных элементов, вырезанных, как правило, из одного и того же образца материала. В простейшем случае используется поочередное переключение элементов и никаких фазовых сдвигов между ними не вводится. Отдельные элементы просто объединяются в группы, например с 1-го по k-й, со 2-го по ![]() . При этом поперечное сканирование несфокусированным пучком, сформированным k соседними элементами, осуществляется путем последовательного переключения на одно межэлементное расстояние. В таком режиме работы межэлементное расстояние выбирается так, чтобы пространственная частота выборки сигнала в акустическом поле была достаточно высокой и в полученном изображении не возникала растровая структура (см. гл. 7).
. При этом поперечное сканирование несфокусированным пучком, сформированным k соседними элементами, осуществляется путем последовательного переключения на одно межэлементное расстояние. В таком режиме работы межэлементное расстояние выбирается так, чтобы пространственная частота выборки сигнала в акустическом поле была достаточно высокой и в полученном изображении не возникала растровая структура (см. гл. 7).
Чтобы обеспечить угловое сканирование и фокусировку ультразвукового пучка, конструкция решетки преобразователей должна удовлетворять достаточно жестким требованиям. Диаграмма направленности каждого отдельного элемента должна быть сравнительно широкой, т. е. поперечные размеры элементов должны быть достаточно малы для того, чтобы полный угол отклонения пучка (например, ±40°) мог быть реализован при приемлемом изменении коэффициента усиления, скажем, на 6 дБ. Вместе с тем диаграмма направленности должна быть достаточно узкой, чтобы обеспечить возможность выделения полезного сигнала на фоне паразитных лепестков решетки. Разработка фазированных решеток преобразователей, обеспечивающих угловое сканирование и фокусировку пучка, является весьма сложной задачей.
Рис. 2.13. Основные типы решеток преобразователей: а — линейная решетка (показана в комбинации с цилиндрической линзой, обеспечивающей фокусировку в направлении, перпендикулярном плоскости сканирования); б — кольцевая решетка.
Обстоятельное рассмотрение этого вопроса проведено в работах [20, 33].
В настоящее время начинают также широко применяться гибридные системы, сочетающие в себе элементы простых решеток с дискретным переключением и фазированных решеток, обеспечивающих угловое сканирование и динамическую фокусировку пучка. В таких системах определенная степень фокусировки достигается за счет введения заданных фазовых сдвигов между элементами отдельной группы. Кроме того, некоторые гибридные системы могут обеспечить небольшое качание пучка с целью снижения когерентности поля излучения-приема [см. гл. 8].
К существенным недостаткам линейных решеток относится то, что формирование заданного профиля пучка и сканирование возможны только в одной плоскости, а именно в плоскости, перпендикулярной продольным осям элементов. Для обеспечения фокусировки вне этой плоскости необходимо использовать акустические линзы или же применять искривленные элементы, создание которых сопряжено с определенными технологическими трудностями.
Кольцевые решетки (рис. 2.13, б) также представляют интерес, хотя они и не получили столь широкого распространения. Принципы их работы обстоятельно рассмотрены в литературе [1, 7, 18]. Преобразователь в виде кольцевой решетки состоит из ряда концентрических кольцевых элементов, образующих плоскую или искривленную поверхность. Введение соответствующих фазовых сдвигов между сигналами, излученными или принятыми каждым элементом или одновременно между сигналами обоих этих типов, позволяет в принципе сформировать волновой фронт с круговой апертурой и любой требуемой формой. На практике часто необходимо, чтобы волновые фронты были сферическими или имели близкую к сферической конфигурацию. Для этой цели используются две различные конструкции кольцевых решеток. В первом случае применяется стационарная геометрическая фокусировка без введения каких-либо фазовых сдвигов в пределах апертуры решетки. Фокусировка на оси достигается с помощью акустической линзы или путем придания определенной конфигурации самой решетке. Во втором случае между соседними кольцевыми элементами вводятся одинаковые фазовые сдвиги. В результате такая решетка превращается в обычную зонную пластинку Френеля, у которой внешние диаметры колец возрастают в последовательности ![]() и т. д., причем площади всех колец равны между собой. В работе [1] показано, что структура акустических полей, генерируемых такими решетками, хорошо согласуется с результатами теоретических расчетов, выполненных в рамках дифракционной теории (см. гл. 1).
и т. д., причем площади всех колец равны между собой. В работе [1] показано, что структура акустических полей, генерируемых такими решетками, хорошо согласуется с результатами теоретических расчетов, выполненных в рамках дифракционной теории (см. гл. 1).
2.6. Акустическое поле гибридной системы «Торонто»
Ранее мы рассмотрели вопросы, связанные с генерацией и исследованием структуры акустических полей. Были проанализированы возможности формирования заданного волнового фронта как с помощью выбора конфигурации поверхности преобразователя, так и методом электронного фазирования. В данном разделе дается краткое описание системы с оптимальными параметрами, разработанной специально для применения в диагностике. На примере этой системы иллюстрируются некоторые принципы, которые обсуждались в предыдущих разделах.
Данную гибридную систему разработали в Торонто Паттерсон и др. [23—25], а также Фостер и др. [9], для визуализации молочной железы. Как будет показано в гл. 8, в этой области возможно применение акустических систем со сравнительно большими апертурами. В этом случае сканирование выполняется через водную среду, обеспечивающую определенную задержку сигнала так, чтобы полезная глубина фокусировки составляла приблизительно 90% от минимального рабочего диапазона. Авторы разработали и сконструировали гибридную систему, схематично показанную на рис. 2.14. Излучателем в этой системе является сферически изогнутая, пятиэлементная кольцевая решетка, выполненная из пьезокерамического материала, а приемником служит восьмисегментный конус из пьезопластика. Поле излучения-приема такой системы представляет собой комбинацию полей двух различных типов. В частности, оно имеет узкий основной максимум, но в то же время и сильно выраженные боковые лепестки, что свойственно фокусированным приемникам с большой апертурой типа аксикона. Было разработано несколько методов, позволяющих снизить уровень боковых лепестков в данной системе. Первый из них относится к методам электронной аподизации волнового фронта, создаваемого кольцевой решеткой, и заключается в подаче на разные кольцевые элементы возбуждающих импульсов различной амплитуды. Установлено, что такой метод является достаточно эффективным, особенно если число кольцевых элементов сравнительно велико, а интервал между элементами мал. Второй предложенный метод подавления боковых лепестков в данной системе сводится к процедуре, названной «антифокусировкой». Согласно этой процедуре, путем сложения в противофазе сигналов от чередующихся секторов конической приемной решетки формируется сложный сигнал «рассогласования», соответствующий только внеосевым эхо-сигналам (боковым лепесткам). После регистрации этот сигнал вычитается из суммарного сигнала всех восьми элементов. В-третьих, авторы обнаружили, что индивидуальные сигналы восьми конусных сегментов были очень близки друг к другу, если мишень находилась на оси, однако различия в них по форме и времени прихода начинали быстро расти по мере удаления мишени от центра. Основываясь на этом наблюдении, авторы продемонстрировали возможность существенного снижения внеосевой чувствительности на основе операции, состоящей в перемножении сигналов от всех восьми сегментов с последующим извлечением корня восьмой степени для восстановления линейности. Здесь можно отметить, что такой подход является, по-видимому, частным примером применения более общего принципа так называемой работки сигналов с минимум энтропии для достижения фокусировки [19].
Рис. 2.14. Гибрвдная сканирующая система <<Торонто>> (вид сбоку в разрезе)
Еще одно потенциальное преимущество использования многосекционных приемных решеток связано с подавлением спекл-шума изображения при когерентном излучении и будет рассмотрено в гл. 8.
2.7. ГЕНЕРАЦИЯ АКУСТИЧЕСКИХ ПОЛЕЙ ДЛЯ ТЕРАПИИ
Терапевтические применения ультразвука подробно рассматриваются в гл. 13. Будет показано, что в силу сложности биологических и биофизических аспектов этой задачи до сих пор полностью не определены точные требования к акустическим полям, предназначенным для терапевтического воздействия на биологические ткани.
Тем не менее следует отметить два существенных момента. Во-первых, в терапевтических приложениях необходимо использовать равномерное «терапевтически эффективное воздействие» в пределах достаточно большой области среды, причем часто требуется, чтобы на границах этой области акустическое поле резко спадало. Во-вторых, само понятие «терапевтически эффективное воздействие» определено несколько произвольно. Иногда оно может соответствовать определенному акустическому параметру (например, произведению амплитуды акустического давления на время воздействия), но часто может быть также сопоставлено и с каким-либо тепловым параметром (например, с минимальным приращением температуры в объеме биологической ткани за время ультразвукового воздействия). В последнем случае реальное акустическое поле является лишь одним из целого ряда факторов, определяющих такой тепловой параметр.
Значение правильного выбора конфигурации акустического поля иллюстрируется тем, что для некоторых приложений это поле должно иметь достаточно «сглаженную» форму, возможно даже с провалом в средней части. Такое поле существенно отличается от остронаправленных полей, которые обычно используются для визуализации в диагностике. Это подтверждают данные, представленные на рис. 2.15 и полученные расчетным путем для двумерного случая. Здесь показан профиль акустического поля, создающего равномерное распределение температуры в ткани с учетом ее теплопроводности [12].
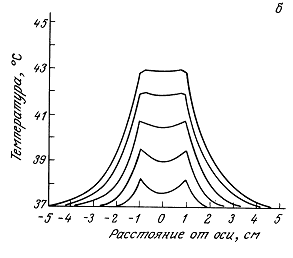
Рис. 2.15. а — Расчетное распределение интенсивности акустического поля в заданной плоскости, обеспечивающее равномерное повышение температуры в образце лишенной кровеносных сосудов мышечной ткани диаметром 2 см после 30-минутного воздействия; б — расчетные распределения приращения температуры под действием данного акустического поля с интервалами в 2 мин. Нижняя кривая — 2 мин воздействия, верхняя — 30 мин [12].
Поскольку на практике создание акустического поля такого профиля представляется малореальным, если вообще возможным, то возникает необходимость в его синтезировании за определенный период времени посредством сканирования остронаправленным пучком по круговой или же какой-либо другой траектории [16].
При использовании ультразвука одна из основных проблем связана с падением интенсивности поля при увеличении глубины проникновения и соответственно с уменьшением доли поглощенной энергии за счет затухания падающего пучка. Если размеры участка воздействия в ткани в направлении, перпендикулярном направлению распространения ультразвука, составляют несколько длин волн, то данная проблема может быть решена путем применения фокусировки.
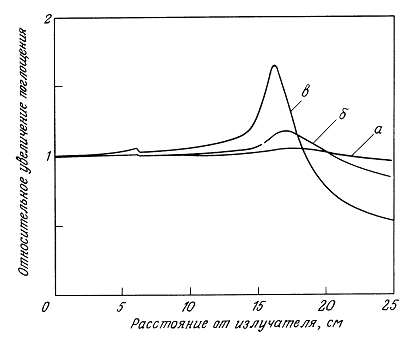
Рис. 2.16. Рост поглощения акустической энергии в биологической ткани за счет нелинейного распространения ультразвукового пучка (явление «акустического пика Брэгга»). Расчет проводится для случая сферического фокусирующего преобразователя диаметром 12 см и фокусным расстоянием 16 см на частоте 1 МГц. От излучателя ультразвуковой пучок проходит водный слой толщиной 6 см и попадает в биологическую ткань с коэффициентом затухания 0,5 дБ/см. Расчеты проводились для трех значений интенсивности на поверхности излучателя — 1 Вт/см (а), 3 Вт/см (б) и 10 Вт/см2 (б). За исключением фокусировки, данные условия воздействия аналогичны условиям, характерным для существующих применений ультразвука в терапии.
Если же требуется воздействовать на участки значительных размеров, то возникает необходимость в сканировании пучком по большой области и указанное преимущество фокусировки в значительной степени теряется. Одно из возможных решений в этом случае может заключаться в создании в фокальной области режима нелинейного распространения ультразвука высокой интенсивности (см. разд. 1.1.8 и 4.3.8). При этом в области фокусировки происходит перекачка энергии из основной частоты в гармонические составляющие высших порядков, поглощение на которых существенно возрастает. Количественный анализ нелинейных эффектов при различных интересных для практики условиях провел Свин-делл [31]. На рис. 2.16 представлены некоторые результаты его расчетов.
Проблема генерации акустических полей требуемой конфигурации представляется достаточно сложной, и для ее решения в настоящее время развивается и постоянно углубляется научная база. Хорошо известные законы волновых процессов налагают определенные принципиальные ограничения на направленность и другие характеристики реальных акустических систем. Однако в современной практике имеющиеся возможности используются далеко не полностью даже в рамках этих ограничений.
1. Arditi, M. Taylor, W. В., Foster, К S., & Hunt, J. W. (1982) An annular array system for high resolution breast echography. Ultrasonic Imaging 4, 1—31
2. Beaver, W. L., Dameron, D. H., & MaCorski, A. (1977) Ultrasonic imaging with an acoustic lens. IEEE Trans. Sonics Ultrasonics SU-24, 235—243
3. Berlincourt, D. (1971) Piezoelectric crystals and ceramics, in Ultrasonic transducer materials (ed. О. E. Mattiat), pp. 63—124. Plenum Press, New York
4. Berlincourt, D. A., Curran, D. R., & Jaffe, H. (1964) Piezoelectric and piezomagnetic
materials and their function in transducers, in Physical acoustics, Vol. 1A (ed. W. P. Mason), pp. 169—270. Academic Press, New York
5. Burckhardt, С. В., Hoffman, H., & Grandchamp, P. A. (1973) The ultrasound axicon: a device for focussing over a large depth. J. acoust Soc. Amer. 54, 1628—1630
6. Cady, W. G. (1964) Piezoelectricity. New York, Dover Publications
7. Dietz, D. R., Parks, S. I., & Linzer, M. (1979) Expanding aperture annular array. Ultrasonic Imaging 1, 56—75
8. Duck, E A. (1981) The pulsed ultrasonic field, in Physical aspects of medical imaging (ed: В. M. Moores et al.). pp. 97—108. Wiley, New York
9. Foster, F. S., Arditi, M., Patterson, M. S., Lee-Chahal, D., & Hunt, J. W. (1983) Breast imaging with a conical transducer/annular array hybrid scanner. Ultrasound in Med. and Biol. 9, 151—164
10. Freedman, A. (1970) Sound field of plane or gently curved pulsed radiators. acoust. Soc. Amer. 48, 221—227
11. Fry, W. J. & Dunn, F. (1962) Ultrasound: analysis and experimental methods in
biological research, in Physical techniques in biological research (ed. W. L. Nastuk) Chap. 6, p. 261. Academic Press, New York
12. Hynynen, K., Watmough, D. J., & Mallard, J. R. (1981) Design of ultrasonic transducers for local hyperthermia. Ultrasound in Med. and Biol. 7, 397—402
13. Jaffe, В., Cook, W. R., & Jaffe, H. (1971) Piezoelectric ceramics. Academic Press, New York
14. Jones, H. W. & Williams, C. J. (1977) Lenses and ultrasonic imaging, in Acoustical holography Vol. 7. (ed. A. F. Metherell) pp. 133—153. Plenum Press, New York
15. Kossoff, G. (1979) Analysis of focusing action of spherically curved transducers. Ultrasound in Med. and Biol. 5, 359—365
16. Lele, P. P. & Parker, K. J. (1982) Temperature distribution in tissues durung local hyperthermia by stationary or steered beams of unfocused or focused ultrasound. Brit. J. Cancer 45, Supplement 5, 108—121
17. Lockwood, J. C. & Willette, J. G. (1973) High speed method for computing the exact solution for the pressure variations in the near field of a baffled piston. /. acoust. Soc. Amer. 53, 735—741
18. Melton, H. E. & Thurstone, F. L. (1978) Annular array design and logarithmic processing for ultrasonic imaging. Ultrasound in Med. and Biol. 4, 1—12
19. Mesdag, P. R., de Vries, D., & Berkhout, A. J. (1982) An approach to tissue characterization based on wave theory using a new velocity analysis technique, in Acoustical imaging, Vol. 12 (E.A.Ash & C. R. Hill, eds) pp. 479—491, Plenum Press, New York
20. Miller, E. B. & Thurstone, F. L. (1977) Linear ultrasonic array design for echosonography. J. acoust. Soc. Amer. 61, 1481—1491
21. Ohigashi, H. (1976) Electromechanical properties of polarized polyvinylidene fluoride films as studied by the piezoelectric resonance method. J. Appl. Phys. 47, 949—955
22. Oloffson, S. (1963) An ultrasonic optical mirror system. Acustica 33, 361—367
23. Patterson, M. S. & Foster, F. S. (1982) Acoustic fields of conical radiators. Trans IEEE-SV 29, 83—92
24. Patterson, M. S., Foster, F. S., & Lee, D. (1982) Sidelobe and speckle reduction for an eight sector conical scanner. Proc. IEEE-SV 29, 169
25. Patterson, M. S. & Foster, F. S. (1983) The improvement and quantitative assessment of B-mode images produced by an annular array/cone hybrid. Ultrasonic Imaging 5, 195—213
26. Penttinen, A. & Luukkala, M. (1976) The impulse response and pressure nearfield of a curved ultrasonic radiator. J. Phys. D.: Appl. Phys. 9, 1547—1557.
27. Shoh, A. (1957) Industrial application of ultrasound — a review: I. High power ultrasound. IEEE Trans. SU-22, 60—71
28. Stepanishen, P. R. (1971) Transient radiation from pistons in an infinite planar baffle. J. acoust. Soc. Amer. 49, 1629—1638
29. Stepanishen, P. R. (1981) Pulsed transmit-receive response of ultrasonic piezoelectric tiansducers. /. acoust. Soc. Amer. 69, 1815—1827
30. Swartz, R. G. & Plummer, J. D. (1980) On the generation of high frequency acoustic energy with polyvinylidene fluoride. IEEE Trans. SU-27, 295—303
31. Swindell, W. (1985) A theoretical study of nonlinear effects with focussed ultrasound in tissues: an acoustic Bragg peak'. Ultrasound in Med. & Biol. 11, 121—130
32. van Kervel, S. J. H. & Thijssen, J. M. (1983) A calculation scheme for the optimum design of ultrasonic transducers. Ultrasonics 21, 134—140
33. Vogel, J., Bom, N.. Ridder, J., & Lancee, C. (1979) Transducer design considerations in dynamic focusing. Ultrasound in Med. & Biol. 5, 187—193.
34. Weight, J. p. (1984) New transducsers for high resolution ultrasonic testing. NDT Int. (G. B.) 17, 3—8.
35. Weight, J. Р. & Hayman, A. J. (1978) Observations of the propagation of very short ultrasonic pulses and their reflection by small targets. J. acoust. Soc. Amer 63, 396—404 (also 66, 945—951)
36. Weyns, A. (1980a,b) Radiation field calculations of pulsed transducers, (a) Part 1.— planar circular, square and annular transducers; (b) Part 2.— spherical disc-and ring-shaped transducers. Ultrasonics 18, 183—188 and 219—223
37. Zieniuk, J. K. & Litniewski, J. (1981) The influense of coherence and wavelength on ultrasonic imaging, in Proc. First Spring School on Acousto-optics — 1981 pp. 198—201, University of Gdansk.
ПРИЕМ И ИЗМЕРЕНИЕ УЛЬТРАЗВУКА
Э. Миллер, К. Хилл
В медицинских или биологических приложениях необходимость в приеме и измерении ультразвука возникает в трех обширных областях. Это получение диагностической информации от пациента, измерение акустических свойств тканей и других сред и измерение акустических полей, которыми могут облучаться живые клетки и ткани, в том числе и ткани пациентов. При этом основной интерес сосредоточен на выяснении связи возможных биологических изменений с физическими параметрами воздействия, т.е. на вопросах дозиметрии. Различные применения предъявляют и различные требования к методу измерения и его особенностям, например возможности получения информации о детальной структуре ультразвукового поля в пространстве и времени или возможности сравнения получаемых результатов с данными каких-либо стандартных методов. Кроме того, требования практического удобства будут различаться для разных применений, например в отношении портативности и механической прочности датчика (зонда) или необходимости прямого преобразования акустического сигнала в электрический. По-видимому, впервые проблемы ультразвуковой дозиметрии были исчерпывающе рассмотрены только в 1973 г. в коллективной монографии [29], а впоследствии еще более детально в 1978 г. О'Брайеном [26].
Ультразвук по определению не воспринимается непосредственно органами чувств человека, и поэтому необходимо использовать какой-то физический эффект или последовательность таких эффектов, чтобы действие ультразвука могло проявиться, причем главным образом количественно. В этой связи очевидны практические удобства тех процессов, которые непосредственно приводят к электрическому сигналу.
Существует значительное число используемых физических эффектов; главные из них перечислены в табл. 3.1. Детально они будут обсуждаться позже, но можно сразу сказать, что наиболее важен пьезоэлектрический эффект, особенно для диагностических применений, поскольку устройства на его основе непосредственно, просто и эффективно преобразуют акустический сигнал в электрический. Все эти эффекты в принципе могут быть использованы в количественных измерениях, т. е. таким путем, что измеренная величина будет однозначно связана через физические константы с интересующими параметрами акустического поля.

Таким образом, выбор метода для конкретной задачи производится с точки зрения удобства его применения, а также точности измерения интересующего параметра акустического поля.
В гл. 2 уже описано применение пьезоэлектрического эффекта в обратной задаче — генерации акустических полей. Важную роль он играет и в приеме акустических волн. Разработано множество конструкций пьезоэлектрических приемников, но большинство из них, по крайней мере применяемых в медицине, имеет форму тонкой пластины или пленки с параллельными поверхностями (либо плоской, либо сферической или другой подобной формы).
Для использования в диагностике в качестве приемников выбираются пластины, вырезанные таким образом, чтобы они могли работать на основном толщенном резонансе. Они же практически могут использоваться и в качестве излучателей или «прожекторов» в эхо-импульсных системах. Современный диагностический преобразователь часто состоит из большого числа элементов, образующих одно- или двумерную решетку. Обычно используется согласованное по фазам соединение достаточного числа элементов таким образом, чтобы сформировать эффективную апертуру, равную по крайней мере 30 длинам волн в облучаемой среде, что является минимальным требованием для достижения удовлетворительной направленности (см. гл. 1). Элементы диагностического преобразователя обычно монтируются, например, с помощью эпоксидного компаунда, на акустически согласованной поглощающей звук подложке (тыльной нагрузке), чтобы сгладить резонансы, которые в противном случае возникнут под действием принимаемого акустического сигнала и вызовут потери в разрешающей способности. На практике внешнюю поверхность преобразователя часто покрывают одним или несколькими четвертьволновыми согласующими слоями (см. разд. 1.7.4) по аналогии с «просветлением» оптических поверхностей. Однако эта процедура несколько снижает положительный эффект тыльной нагрузки, так как вызывает неоднородности в частотной характеристике и накладывает ограничения на ширину полосы пропускания.
Не стоит рассчитывать, что преобразователь, изготовленный таким способом, будет иметь однородную чувствительность по своей апертуре. Реальная чувствительность даже одноэлементных преобразователей имеет существенные неоднородности с возможными провалами на периферии и нередкими аномалиями, связанными с непредсказуемыми дефектами в сцеплении согласующих и поглощающих слоев. Такие отклонения от «идеального» поведения изменяют диаграмму направленности приемника. В гл. 8 мы вернемся к обсуждению работы пьезоэлектрических приемников в диагностической аппаратуре.
Согласованность фаз на большой апертуре, необходимая для обеспечения высокого пространственного разрешения при получении изображения, становится главным недостатком при использовании преобразователя для количественной оценки принимаемой энергии независимо от направления ее прихода (например, при измерении коэффициентов затухания).
Такая проблема возникает при использовании фазочувствительного приемника для количественных измерений параметров распространения, например коэффициентов затухания, в таких средах, как ткани человека, в которых неоднородности коэффициента преломления могут заметно искажать падающий волновой фронт. В этой ситуации компоненты волны, падающие на различные точки преобразователя, могут взаимно компенсировать электрический откликпреобразователя и тем самым недопустимым образом исказить измерение полной акустической мощности [6]. Это иллюстрация того, что к приемникам, предназначенным для получения изображений и для количественных измерений, могут предъявляться различные требования. В то же самое время это призыв к проявлению большой осторожности при количественной интерпретации акустических изображений.
Конструкторские требования к приемникам, предназначенным для использования в дозиметрии и измерениях свойств материалов, будут значительно отличаться от требований к приемникам, предназначенным для диагностического применения, особенно в отношении чрезвычайно высоких требований к чувствительности. В диагностике всегда выдвигается требование получения максимальной информации при заданной экспозиции, которой подвергается пациент. Для измерений свойств материалов или растворов в узкой полосе частот или некотором наборе частот хорошим приемником является кварц, несмотря на его относительно низкий коэффициент электромеханической связи. В то же время для таких измерений, которые требует дозиметрия (см. разд. 3.8), когда наиболее важны малые физические размеры и однородность частотной характеристики, удобно использовать пьезокерамические или пьезополимерные (из поливинилиденфторида) приемники в нерезонансных условиях.
Желаемые характеристики и методы калибровки миниатюрных пьезоэлектрических подводных приемников (гидрофонов), предназначенных для количественных измерений акустических полей в частотном диапазоне 0,5—15 МГц, были предметом официального международного обсуждения и отражены в согласованных рекомендациях [17]. Хотя измерения сильно неоднородных полей в идеале требуют приемников с линейными размерами, много меньшими длины волны в исследуемой среде (например, 0,1 мм для 15 МГц в воде), пока еще невозможно удовлетворить этому требованию без неприемлемых потерь в чувствительности. Вполне удовлетворительным компромиссом почти для любой реальной ситуации является чувствительный приемник диаметром около 0,5—1 мм. Разработано большое число таких приемников; некоторые из них выпускаются серийно: например, выполненные на основе пьезополимерных пленок [20] или пьезокерамических пластинок с толщенным резонансом около 30 МГц [21]. Они весьма полезны для изучения пространственной структуры полей, хотя последняя конструкция и имеет неоднородную частотную характеристику, частично из-за радиальной моды колебаний пьезокерамического диска диаметром 1 мм, частота которой около 2 МГц.
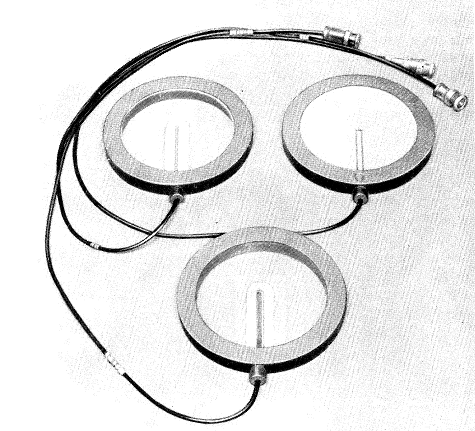
Рис. 3.1а — Образцы акустических гидрофонов из растянутых пленок поливинилиденфторида. Во всех образцах пленка растянута на жестком кольце с внутренним диаметром около 120 мм. Представлены три образца одноэлементных гидрофонов, зона чувствительности которых площадью 0,25—1,0 мм2 находится в центре мембраны и создана областью перекрытия двух золотых электродов, напиленных в вакууме на обе стороны пленки.
Поэтому более удовлетворительной кажется конструкция в виде натянутой поливинилиденфторидной пленки диаметром около 10 см, на которой чувствительная зона диаметром 1мм создана напылением в вакууме пары электродов, расположенных напротив друг друга [35]. Образцы такого типа гидрофонов показаны на рис. 3.1. Важно знать направленность таких приемников; полезное введение в данную проблему приведено в работе [33].

Рис. 3.16 - Антенная решетка из 21 элемента, изготовленная по той же технологии (С разрешения д-ра Р. С. Престона и Королевской национальной физической лаборатории.)
Изучение акустического поля можно провести, прибегнув к механическому сканированию заданной области чувствительным элементом такого приемника или изготовив его в виде многоэлементной решетки, и, таким образом, сформировать очень практичную и точную измерительную систему.
Калибровка такого гидрофона производится в известных акустических полях, выбранных так, чтобы перекрыть интересующий диапазон частот, при этом амплитуды самих калибровочных полей должны быть выражены через основные физические величины, например массу, длину и время. Как показано в последующих разделах этой главы, имеется несколько вариантов этой процедуры, но действующая рекомендация Международной электротехнической комиссии [17] основана на использовании для пьезоэлектрических преобразователей принципа взаимности. Существует также намерение Международной электротехнической комиссии в конце концов рекомендовать альтернативную процедуру, основанную на измерении радиационного давления (см. разд. 3.4), хотя пока еще нет уверенности, что подобные методы измерения в достаточной мере обоснованы и изучены, чтобы использовать их в официальных рекомендациях.
3.2.1. КАЛИБРОВКА ГИДРОФОНА МЕТОДОМ ВЗАИМНОСТИ
Теорема взаимности, введенная в акустику Рэлеем, в соответствии с целями данного раздела может быть сформулирована в следующем виде (более полное изложение есть в работах [23, 11]).
Если преобразователь, работающий как излучатель, возбуждается током у, амплитуда звукового давления в свободном поле на расстоянии d метров от акустического центра излучателя на его акустической оси в дальнем поле или в зоне сферической волны задается следующим образом:
![]()
где S — чувствительность преобразователя по току в режиме излучения.
Для конкретного преобразователя S может быть константой в определенном диапазоне величин p и j, и тогда характеристика в режиме излучения будет линейной.
Подобным образом, если преобразователь, работающий как гидрофон, размещен так, что его акустический центр находится в дальнем поле с амплитудой звукового давления Р, а его акустическая ось нормальна к волновому фронту в этой точке, то напряжение холостого хода на клеммах преобразователя будет
![]()
где М — чувствительность по напряжению в свободном поле. Все рассуждения верны при условии, что преобразователь работает в линейном режиме.
Для обратимых преобразователей
![]()
где J — константа, называемая коэффициентом (или параметром) взаимности для сферических волн, который имеет величину (в единицах СИ)
![]()
где ![]() — плотность среды, f — частота, на которой ведутся измерения. Соответствующие параметры взаимности могут быть определены для плоской и цилиндрической волн.
— плотность среды, f — частота, на которой ведутся измерения. Соответствующие параметры взаимности могут быть определены для плоской и цилиндрической волн.
Покажем, что теорема взаимности дает возможность, по крайней мере в принципе, калибровать гидрофон путем измерения основных физических величин: напряжения, тока, длины.
Предположим, что имеется три преобразователя, обозначенных номерами 1, 2, 3, один из которых, например № 3, взаимный. Они собираются в пары при соблюдении условий свободного поля, и измеряется передаточный импеданс каждой пары, как показано ниже.

Исходя из определений, измерения дают следующее:
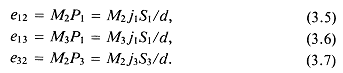
![]()
Из (3.5) и (3.6) получаем
поскольку ![]() (по определению), то
(по определению), то
и из (3.7) и (3.9) следует
![]()
т. е. та самая калибровка, которая требовалась.
Другой метод калибровки, так называемый метод самовзаимности, который предусматривает использование только одного преобразователя, описан в ранее упомянутой рекомендации МЭК [17], в которой приведено детальное описание экспериментальных процедур и необходимых корректировочных коэффициентов.
Обязательным условием применения метода, описанного выше, является необходимость поиска удобного преобразователя, являющегося действительно взаимным. Этот вопрос, особенно важный для гидроакустики, широко обсуждался, в частности, Боббером [2], который установил, что большинство линейных, пассивных и обратимых преобразователей являются взаимными, за исключением, возможно, области острого резонанса. На практике можно устранить сомнения, касающиеся невзаимности, путем повторения описанной выше процедуры калибровки с помощью трех преобразователей, используя большое число различных комбинаций преобразователей и проверяя самосогласованность результатов.
Несколько дополнительных методов калибровки гидрофонов будут описаны в последующих разделах этой главы.
3.2.2. МЕТОДЫ ПРОВЕДЕНИЯ ИЗМЕРЕНИЙ В ТОЧКЕ
Недостаток большинства имеющихся в настоящее время гидрофонов обусловлен конечностью их размеров. Фактически они не измеряют акустическое давление в точке, а интегрируют его по своей апертуре, обычно размером около 1 мм, т. е. порядка нескольких длин волн в воде в диапазоне частот 1 — 10 МГц. Эту проблему можно решить двумя способами: сконструировать гидрофон с очень маленькой приемной апертурой или математически, путем обращения свертки, отделить влияние апертурной функции на наблюдаемый отклик преобразователя с конечной апертурой.
Этот недостаток неизбежно приводит к потере чувствительности. Однако имеются сообщения об успешных применениях очень маленьких приемников, и в качестве интересного примера на рис. 3.2 показана конструкция одного из них. Его апертура определяется площадью контакта между тонкой мембраной и вершиной твердого конуса. Изолирующий объем воздуха препятствует распространению звука через мембрану куда-либо еще. В литературе нет сообщений о достоверной калибровке такого гидрофона, хотя его использование для качественных измерений акустических полей с высоким разрешением представляется полезным.
Основа для решения проблемы конечной апертуры путем обращения свертки для частного случая одной звуковой частоты дана в разд. 1.4. Если представить временную зависимость как ![]() , то решение для втекающей в преобразователь бегущей волны можно записать в следующем виде:
, то решение для втекающей в преобразователь бегущей волны можно записать в следующем виде:
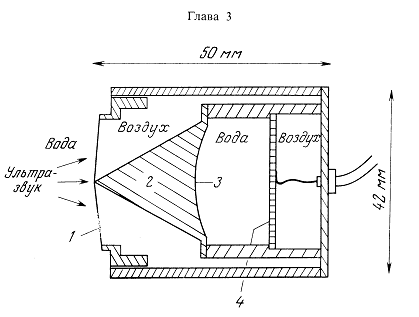
Рис. 3.2. Конструкция гидрофона с высоким пространственным разрешением. Зоной чувствительности является точка контакта между коническим алюминиевым волноводом и майларовой пленкой, нагруженной остальной площадью на воздух [7]. ![]() — Майларовая пленка; 2 — алюминиевый конус; 3 — акустическая линза; 4 — электроакустический преобразователь.
— Майларовая пленка; 2 — алюминиевый конус; 3 — акустическая линза; 4 — электроакустический преобразователь.
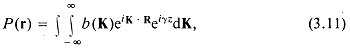
![]() Источник звука лежит в плоскости z = 0.
Источник звука лежит в плоскости z = 0.
Заметим, что угловой спектр плоской волны (см. гл. 1) в уравнении (3.11) не зависит от положения и поэтому характеризует звуковое поле в пространстве.
Давление Р(r) может рассматриваться как давление, измеряемое точечным ненаправленным приемником в точке r пространства. Если приемник имеет конечные размеры, скажем это диск радиусом rd и с центром в точке ![]() в плоскости х, у для данного z0, тогда r можно заменить на R + D. Координата D может быть использована для усреднения давления по круглому диску. Таким образом,
в плоскости х, у для данного z0, тогда r можно заменить на R + D. Координата D может быть использована для усреднения давления по круглому диску. Таким образом,
![]()
Уравнение (3.11) затем преобразуется
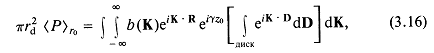
где из разд. 1.5 мы знаем, что
![]()
где ![]()
Обращение уравнения (3.16) дает
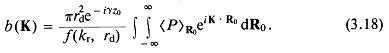
Выражение (3.18) совместно с (3.11) показывают, что данные, полученные с помощью приемника в виде поршня конечного размера в плоскости z0, могут быть откорректированы так, чтобы дать угловой спектр плоской волны b(K), соответствующий спектру, полученному идеальным ненаправленным приемником. Эта корректировка осуществляется делением обычного интеграла, включающего усредненное по пространству давление, на f(kXi rd) — единственную функцию, зависящую от радиуса поршня приемника, rd. Подставляя b(K) из (3.18) в (3.11) и проводя указанное интегрирование по кх и ку, можно получить идеальные данные для давления в любой точке пространства.
На практике часто возникает необходимость в применении этой процедуры к широкополосным устройствам, т. е. в соответствующем диапазоне частот. К сожалению, практические методы расширения описанного выше метода одночастотного обращения свертки на случай широкополосных устройств еще не разработаны.
Характеристики акустического поля могут быть определены из измерений локального смещения d, вызванного на поверхности действием компоненты волны сжатия, нормальной к этой поверхности.
Одним из первых устройств, использующих этот подход, был конденсаторный микрофон (см., например, [10]). В нем акустическая волна падала нормально на одну из плоскопараллельных обкладок конденсатора с воздушным диэлектриком, а результирующее отклонение затем определялось через известные величины, например расстояние между обкладками и заряд. Однако емкость такого микрофона становится чрезвычайно малой при попытке проведения измерений с высоким пространственным разрешением, а неопределенности соответственно возрастают.
Более приемлемый, хотя и сложный, способ измерения акустических смещений позволяет осуществить оптическая интерферометрия. Реализацию этого способа можно проводить различным образом, например [24], заставляя исследуемый акустический пучок отражаться почти нормально от прилегающей к жидкости стороны очень тонкой растянутой мембраны или поверхностной пленки, образующей границу раздела между воздухом и озвучиваемой жидкостью. Обращенная к воздуху сторона мембраны изготавливается в виде оптического отражателя и последовательно сканируется (опять-таки при почти нормальном падении) узким пучком света, например от лазера, образуя одно плечо оптического интерферометра (см. также разд. 9.2 и рис. 9.3). Если вспомнить (см. разд. 1.7.1), что при интенсивности 10 мВт/см2 на частоте 2 МГц акустическое смещение в воде порядка длины световой волны, становится понятным, что такой прибор обладает большими возможностями для быстрой регистрации наиболее сложных профилей звуковых пучков с высоким пространственным и временным разрешением. При практической реализации возникают трудности, особенно в отношении изоляции от посторонних вибраций. Так что это устройство пока еще остается специализированным лабораторным прибором, применимым для точной калибровки гидрофонов.
3.4. ИЗМЕРЕНИЯ РАДИАЦИОННОГО ДАВЛЕНИЯ
Хорошо известно физическое явление — возникновение постоянной силы, называемой радиационным давлением; его испытывает тело, которое поглощает или отклоняет пучок излучаемой энергии.
Поскольку радиационное давление может быть измерено с большой точностью и, как будет показано, однозначно связано с параметрами акустического поля, такой способ позволяет относительно просто измерять параметры акустического поля в основных физических единицах.
В недавнем прошлом теоретическое описание радиационного давления являлось предметом активной дискуссии [22, 32]. Теория явления сложна и включает в себя решение акустической задачи во втором порядке приближения с соответствующими граничными условиями и преобразование координат. Используя приближение плоской волны, можно существенно упростить задачу.
Общая постановка задачи, сохраняющая полностью векторный характер, как показано в разд. 1.8, имеет определенные достоинства. Во-первых, более общие выражения позволяют получить решения для более широкого набора геометрий мишеней. Во-вторых, граничные условия в такой постановке задачи приводят к необходимости применять условия «свободного поля» (так называются условия, при которых звук, рассеянный мишенью, не попадает ни на мишень, ни на преобразователь).
Последний результат разд. 1.8 (см. (1.216)) показывает, что
![]()
т. е. радиационная сила F, действующая на объект, равна интегралу по всей поверхности объекта от вектора, направленного по внутренней нормали и равного средней по времени плотности акустической энергии ![]() в каждой точке.
в каждой точке.
Выражения (1.207), (1.212) и (1.214) из гл. 1 позволяют получить другое соотношение для радиационной силы, связывающее ее с разностью между кинетической и потенциальной энергиями в единице объема L следующим образом:
![]()
Область интегрирования должна быть свободной от акустических источников или поглотителей. Она ограничивается поверхностью преобразователя и той частью мишени, которая рассеивает или поглощает акустическую энергию. Другие поверхности, ограничивающие R, должны быть выбраны так, чтобы все члены уравнения были равны нулю за счет большого расстояния, направления излучения или условий распространения бегущей волны (![]() и F равны нулю).
и F равны нулю).
Если мишенью является плоский идеальный поглотитель и поверхность преобразователя образует плоский поршень, параллельный мишени, то для обеих поверхностей можно написать
![]()
Уравнение (3.20), таким образом, дает
![]()
Средняя по времени общая излученная преобразователем мощность равна
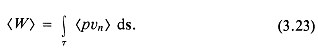
Произведение ![]() , как показано в разд. 1.2, является просто компонентой интенсивности
, как показано в разд. 1.2, является просто компонентой интенсивности ![]() , где
, где ![]() - координата, нормальная к поверхности преобразователя или поглотителя.
- координата, нормальная к поверхности преобразователя или поглотителя.
Следовательно, выражение (3.22) упрощается до вида
![]()
где Fp — сила, действующая на плоскую поверхность.
Для конической мишени с углом полураскрыва ![]() установлено [3], что радиационная сила Fc звукового пучка, параллельного оси конуса, равна
установлено [3], что радиационная сила Fc звукового пучка, параллельного оси конуса, равна
![]()
где Fa — сила, действующая на идеальный плоский поглотитель R — амплитудный коэффициент отражения. Круговой конус с углом полураскрыта ![]() = 45° был рассмотрен в работе [251 В этом случае
= 45° был рассмотрен в работе [251 В этом случае
![]()
Эти два случая представляют простейшие и наиболее часто применяемые геометрии поглощающей (Fp) и отражающей (Fc) мишеней. В более общем случае, как будет показано,
![]()
где k — константа, зависящая от геометрии взаимодействия- для полного поглощения пучка k = 1, для полного нормального отражения k = 2 и для частичного поглощения или произвольного отражения 0 < k < 2. Следует отметить, что величина ![]() является линейной плотностью энергии в падающем пучке.
является линейной плотностью энергии в падающем пучке.
Вышеприведенные зависимости позволяют измерить интенсивность акустического поля в основных физических единицах и, таким образом, послужить основой для абсолютных акустических измерений. Такие измерения распадаются на две широкие области применения: 1) измерения общей мощности пучка, при этом сечение мишени должно превышать общее эффективное сечение пучка; 2) измерения локальной интенсивности, когда мишень должна быть малой по отношению к характерным размерам неоднородностей пучка. Измерения с мишенями промежуточного размера иногда проводятся, но, как правило, приводят к большим неточностям. Измерения с использованием радиационной силы могут быть также разделены на измерения, когда производится непосредственная оценка мощности или интенсивности, и на измерения, проводимые как часть процедуры калибровки вторичных приборов, таких как гидрофоны.
3.4.1. ИЗМЕРЕНИЯ С БОЛЬШОЙ МИШЕНЬЮ
Существует множество конструкций устройств с большими мишенями, причем чаще всего отражающими, чтобы избежать температурных аномалий, связанных с нагревом поглощающих мишеней. Устройства отличаются по чувствительности и методам измерения силы. Имеются приборы, основанные на стандартных аналитических весах [15, 31] (рис. 3.3), на электромагнитных компенсационных приборах нулевого отклонения [9] и компенсационных приборах поплавкового типа [34]. Ориентируясь на их акустические свойства (т. е. исключая электрические и механические погрешности, обусловленные конструкцией), точность измерений таких приборов можно оценить примерно в 5%. Она снижается, если возможны проникновение энергии в мишень или аномальные переизлучения.
Измерения радиационной силы может использоваться для калибровки гидрофонов по следующей процедуре. Сначала определяют общую мощность, проходящую через поверхность постоянной фазы в поле гармонического акустического источника. Затем необходимо гидрофоном просканировать целиком апертуру, перекрывавшуюся ранее мишенью радиометра, и измерить напряжение холостого хода гидрофона ![]() , которое связано с чувствительностью следующим образом (см. выражение (3.2)):
, которое связано с чувствительностью следующим образом (см. выражение (3.2)):
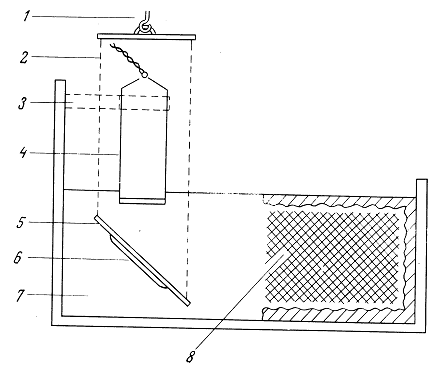
Рис. 3.3. Ультразвуковой радиометр на основе химических микровесов, обладающий точностью 0,3 мВт. Пучок целиком отражается пластинкой, наклоненной под углом 45° (выше критического угла для поверхности раздела вода — алюминий). Для уменьшения влияния поверхностного натяжения отражающая пластина подвешена на трех тонких, диаметром 45 мкм, нейлоновых нитях. Компенсация температурной зависимости кажущегося веса пластинки в воде достигается наклеиванием на ее обратную сторону соответствующей массы парафина [15]. ![]() — Точка прикрепления к весам; 2 — нейлоновая нить; 3 — крепление преобразователя; 4 — преобразователь; 5 — отражающая пластина; 6 — парафин; 7 — дегазированная вода; 8 — акустическая ловушка, состоящая из рассеивателей и поглотителей.
— Точка прикрепления к весам; 2 — нейлоновая нить; 3 — крепление преобразователя; 4 — преобразователь; 5 — отражающая пластина; 6 — парафин; 7 — дегазированная вода; 8 — акустическая ловушка, состоящая из рассеивателей и поглотителей.
где М — чувствительность гидрофона по напряжению в свободном поле, измеряемая в В/Па.
Если в окрестности апертуры радиометра геометрия поля близка к полю плоской волны, что может быть достигнуто соответствующим выбором калибровочного поля и проверено экспериментально, то
![]()
при этом связь между р и ![]() для плоской волны —
для плоской волны —
![]()
Таким образом, локальные значения для ![]() даются выражением
даются выражением ![]()
Теперь из (3.28) и (3.31) следует, что
![]()
где ![]() обозначает усреднение по времени.
обозначает усреднение по времени.
Интегрирование средней по времени интенсивности по поверхности постоянной фазы позволяет найти общую мощность, которая ранее была определена по радиационному давлению. Таким образом,
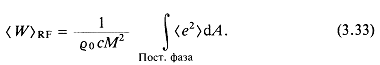
Обращая выражение, находим чувствительность гидрофона
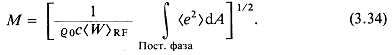
На практике точность этого способа существенно ограничивают краевые эффекты на мишени радиометра и трудность с точным определением фазы и амплитуды поля на периферии пучка. Однако трудности эти преодолимы, и есть уверенность, что способ измерения радиационного давления для калибровки гидрофонов будет принят МЭК в дополнение к методу взаимности, описанному выше.
3.4.2. ИЗМЕРЕНИЯ С МАЛОЙ МИШЕНЬЮ
Если методика измерения радиационного давления используется для определения локальных величин интенсивности, важно, во-первых, чтобы размеры мишени были значительно меньше характерных размеров пространственных неоднородностей полей интенсивности, и, во-вторых, чтобы взаимодействие волна — мишень описывалось простыми и удобными для расчетов зависимостями. Наилучший способ удовлетворить последнему условию — это применить сферическую мишень. Обычно для мишени используют стальной шарик от подшипника. Вычисления для этого случая приведены в работе [14], результаты представлены в безразмерном виде через величину ![]() — отношение силы радиационного давления Fr действующей на сферу, к площади поперечного сечения (а — радиус сферы) и средней плотности энергии
— отношение силы радиационного давления Fr действующей на сферу, к площади поперечного сечения (а — радиус сферы) и средней плотности энергии ![]() .
.
В одной из конструкций для подвески такой сферы используются две нити равной длины таким образом, чтобы образовать маятник. Если сила радиационного давления отклоняет такой маятник на расстояние d в горизонтальном направлении, то величина этой силы Fx легко находится из выражения
![]()
где L — длина перпендикуляра, опущенного от линии, соединяющей точки подвеса нитей к центру сферы (![]() ), т — масса сферы плюс масса необходимой части системы подвеса, причем обе с учетом силы выталкивания воды, g - ускорение свободного падения.
), т — масса сферы плюс масса необходимой части системы подвеса, причем обе с учетом силы выталкивания воды, g - ускорение свободного падения.
Таким образом, Fr, найденная экспериментально, позволяет определить интенсивность ультразвукового поля по следующей зависимости:
![]()
Для этой конструкции важно, чтобы нити подвеса были достаточно тонкими и не вносили существенных искажений в поле, а их прикрепление не изменяло профиль сферы или ее моды собственных колебаний.
Результаты вычисления величины Yp для некоторых типичных случаев показаны на рис. 3.4. Видно, что, во-первых, взаимодействие имеет сложную частотную зависимость и, во-вторых, для приемлемой точности требуется очень хорошее знание физических свойств материала сферы.
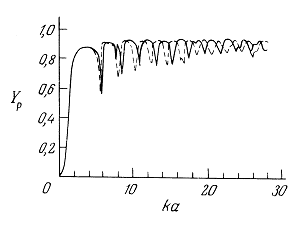
Рис. 3.4. Величины Yp (см. текст), рассчитанные для шариков, изготовленных из двух сортов стали с немного отличающимися физическими свойствами: скорость звука для поперечных волн 3252 мс-1 (сплошная линия) и 3089мс-1 пунктирная линия), скорость продольных волн равна 5949 мс-1 в обоих случаях [36].
Фактически, однако, в большинстве приведенных в литературе результатов игнорируется влияние затухания звука в материале сферы. В таком случае использование материала, обладающего высоким затуханием звука, может привести к сглаживанию частотной зависимости и более предсказуемым результатам [1], хотя в этом случае могут стать заметными последствия нагрева мишени и их придется учитывать.
Возможно, что наиболее универсальный метод определения энергии, связанной с различными физическими явлениями, - тот, который основан на полном преобразовании ее в измеримое тепло. Что же касается изучаемой здесь энергии ультразвука, то по аналогии с измерениями радиационного давления возможны два подхода: а) измерение общей мощности пучка, захватываемого полностью апертурой приемника; б) измерение локальной величины интенсивности в определенной точке профиля пучка по локальной скорости увеличения температуры в среде с известным коэффициентом поглощения.
Как и в случае измерений радиационного давления, калориметрический способ измерения общей мощности пучка очень привлекателен тем, что в принципе он осуществляется с прямым использованием основных физических величин. Если, однако, он используется для калибровки вторичных приборов, таких как гидрофоны, то снова возникают неопределенности, связанные с точным распределением энергии на краях пучка, где интенсивность мала, и с краевыми эффектами, возникающими при входе пучка в окно калориметра.
Полезным применением ультразвуковой калориметрии, где эти проблемы не возникают, является измерение общей акустической мощности преобразователя при условии, что звуковой пучок целиком направляется в калориметр. Этот способ успешно применяется, например, при калибровке мощных преобразователей, используемых при лечении болезни Меньера (см. гл. 13). Конструкция калориметра показана на рис. 3.5.
Это конкретное применение не требует очень большой чувствительности, и показанное простое устройство вполне пригодно для этой цели. Однако могут быть разработаны калориметрические методы очень высокой чувствительности; осуществимость этого подтверждает использование калориметрии в такой специфической области, как измерение энергии пучков ионизирующего излучения [19].
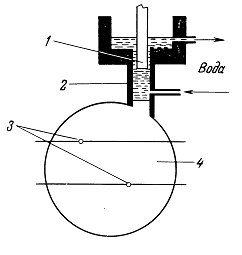
Рис. 3.5. Образец калориметра для измерения общей мощности пучка. Предназначен для калибровки ультразвуковых пучков преобразователей для лечения болезни Меньера [39]. 1 — Проверяемый преобразователь; 2 — охлаждающая водяная рубашка для предотвращения прямой передачи тепла, выделяющегося из-за внутренних потерь в преобразователе; 3 — термопары; 4 — четырех-хлористый углерод. Прибор может быть прокалиброван с помощью встроенной нагревательной обмотки (не показана).
Современный чувствительный прибор для диапазона частот ультразвука, применяемого в медицине, описан в работе [37].
Измерения локальных величин интенсивности калориметрическими методами возможны с помощью иного подхода. В этом случае основной задачей является достижение высокого пространственного разрешения и наиболее подходящий метод — использование термопар из тонких проволочек наряду с малыми термисторами, дающими более высокую чувствительность по температуре ценой уменьшения пространственного разрешения. Термопарная дозиметрия хорошо описана в работе [12], где она была использована для измерения пространственных распределений и абсолютных значений интенсивности мощных и фокусированных звуковых пучков. Применяемая методика включает в себя изготовление термопары из проволочек диаметром приблизительно 0,01 мм и помещение ее в звукопоглощающую жидкость, например касторовое масло, коэффициент поглощения которого в рабочем диапазоне температур и частот хорошо известен. При этом обеспечивается, чтобы жидкость и содержащий ее сосуд, который может иметь окна из тонкой полимерной пленки, были хорошо акустически согласованы с внешней средой. Источник звука возбуждается таким образом, чтобы излучался одиночный прямоугольный акустический импульс длительностью около одной секунды; при этом записывается зависимость термоэлектрического потенциала от времени. Эта запись имеет обычную форму, показанную на рис. 3.6, где первоначальный участок быстрого роста соответствует вязкому взаимодействию между проволочкой и средой.
Рис. 3.6. Запись термоЭДС термопары из тонких проволочек, погруженной в поглощающую среду при воздействии импульса ультразвука длительностью 1 с.
Последующая фаза температурной записи вызывается поглощением звука в объеме жидкости, и ее первоначальный, приблизительно линейный наклон является непосредственной мерой локального коэффициента поглощения. При применении в неоднородных, в частности сильно сфокусированных, полях метод несвободен от влияния рассеяния тепла, теплопроводности материала проволочек и акустической нелинейности. Следует отметить, что в случае, когда термопара или другой приемник помещается непосредственно в неизвестную среду, метод дает истинный коэффициент поглощения и, таким образом, обеспечивает информацию, дополнительную к данным по измерению коэффициента затухания (гл. 4).
3.6. МЕТОДЫ ОПТИЧЕСКОЙ ДИФРАКЦИИ
Можно ожидать, что быстрые изменения давления, связанные с распространением акустических возмущений, будут вызывать соответствующие изменения оптического коэффициента преломления вследствие эффекта Рамана — Ната. Хороший обзор теоретических исследований в этой области и описание общепринятых параметров даны в работе [18]. Такие изменения коэффициента преломления были зарегистрированы [30], и были выдвинуты предложения по их использованию в количественных измерениях параметров акустических пучков [4, 8]. Описание типичной аппаратуры для проведения таких измерений приведено в подписи к рис. 3.7.
Параллельный световой пучок проходит через озвученную среду в направлении, нормальном к оси измеряемого акустического пучка, и затем фокусируется линзами или зеркалом. В этой ситуации звуковой пучок действует подобно фазовой решетке, и часть энергии нулевого порядка, т. е. исходного пучка, дифрагирует в высшие порядки спектра. Интенсивность света в каждом дифракционном порядке является функцией амплитуды вызванного ультразвуком изменения оптического коэффициента преломления и оптической длины пути через звуковой пучок.
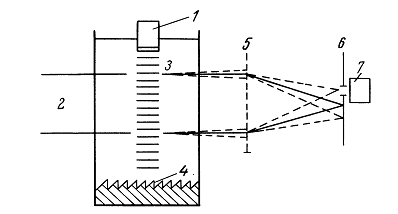
Рис. 3.7. Устройство для измерения оптической дифракции, вызванной изменениями плотности в ультразвуковом пучке: ![]() — ультразвуковой излучатель; 2 — источник света с параллельным пучком; 3 — ультразвуковой пучок в воде; 4 — акустический поглотитель; 5 — собирающая линза; 6 — щель; 7 — фотодиод. Первый порядок оптической дифракции показан штриховыми линиями.
— ультразвуковой излучатель; 2 — источник света с параллельным пучком; 3 — ультразвуковой пучок в воде; 4 — акустический поглотитель; 5 — собирающая линза; 6 — щель; 7 — фотодиод. Первый порядок оптической дифракции показан штриховыми линиями.
Эта функция может быть оценена для типичных условий большинства медицинских пучков. Более подробное описание этой возможности и библиография даны в работе [26].
Реализация этого принципа в количественных измерениях наталкивается на значительные сложности особенно из-за неоднородности распределения амплитуды давления по сечению звукового пучка. Однако в работе [28] приведены данные сравнительных измерений акустической мощности в диапазоне частот 1—8,7 МГц, проведенных оптическим методом и радиометром. Было найдено хорошее согласие между данными, полученными двумя методами, за исключением случаев, в которых различия между результатами этих методов были обусловлены априорными предположениями о форме звукового поля.
В дополнение к использованию в количественных измерениях оптическая дифракция создает основу для очень полезных качественных методов визуализации акустических полей бегущих и стоячих волн, а также формы волновых пакетов и их эволюции во времени.
Вернемся к рис. 3.7. Если оптическую щель разместить так, чтобы отделить свет, попадающий только в один дифракционный порядок, например первый, и использовать дополнительные оптические средства для формирования изображения плоскости, которую
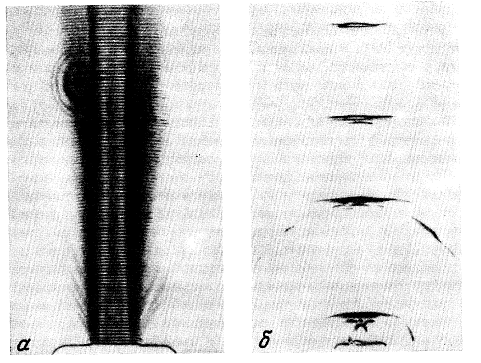
Рис. 3.8. Шлирен-изображения. а — Поле непрерывных волн от плоского преобразователя, подобного тем, которые используются в терапии; б — импульс от линейной решетки преобразователей, используемой для медицинской визуализации в реальном масштабе времени. Импульс сфотографирован в четырех точках при его распространении на разных расстояниях от преобразователя, который и на частях а и на б совмещён с нижним краем фотографии. Заметно разделение импульсного волнового пакета на плоскую и краевую компоненты, как описано в разд. 2.3. (С разрешения д-ра Р. С. Престона и Королевской национальной физической лаборатории.)
пересекает акустический пучок, то такое изображение будет выглядеть как темное поле, промодулированное в соответствии с интегралом по оптическому пути от локальных величин отклонений амплитуды давления. Пример такого, так называемого шлирен (т. е. полосатого)-изображения показан на рис. 3.8.
Добавление аппаратуры для стробоскопического наблюдения, например импульсного источника света, позволяет визуализировать волновой пакет в пучке импульсного источника и продемонстрировать детально особенности его взаимодействия с отдельными мишенями и границами раздела.
3.7. ДРУГИЕ МЕТОДЫ ПРИЕМА И ИЗМЕРЕНИЯ ЗВУКА
Имеется значительное число других физических явлений, которые могут быть использованы для регистрации и измерения параметров акустических полей и их распределений в пространстве и времени. Здесь можно дать только краткое описание некоторых из них.
Так называемый акустоэлектрический эффект обусловлен взаимодействием энергии распространяющейся акустической волны с системой фотовозбужденных носителей зарядов в фоточувствительном полупроводниковом кристалле, таком как сульфид кадмия [38]. Эффект обусловлен конечным временем отставания от волны отклика носителей зарядов, которые увлекаются волной, подобно электронам в линейном ускорителе, увеличивая при этом градиент электрического потенциала. В известном смысле это явление вызывает прямое преобразование акустической энергии в электрическую и имеет некоторую аналогию с пьезоэлектрическим эффектом, но отличается от него тем, что не обладает фазовой чувствительностью. Это свойство используется в приемниках для измерения коэффициентов затухания, где, как обсуждалось выше, ошибочные и непредсказуемые изменения фазы на поверхности фазо-чувствительного приемника могут существенно искажать результаты измерений [5].
Один из главных недостатков ультразвука по сравнению со светом или рентгеновскими лучами — отсутствие кйкого-либо ультразвукового аналога процессу фоторегистрации. Были сделаны попытки найти замены, но ни одна из них не нашла широкого применения. Было показано, например, что процесс химического проявления равномерно экспонированной фотопленки ускоряется под действием ультразвука вследствие возникновения микропотоков и, таким образом, дает возможность, хотя и достаточно грубо, непосредственно зарегистрировать изменения интенсивности в звуковом пучке. В работе [40] был описан аналогичный метод визуализации поля, основанный на явлении фонофореза — увеличения проникновения и поглощения молекул краски в бумаге или подобном материале в зоне высоких акустических смещений; при этом утверждалось, что метод позволяет проводить количественные измерения параметров поля. Еще одно устройство, так называемая ячейка Польмана, использует стремление маленьких удлиненных частиц, например микроскопических металлических опилок, в жидкой суспензии определенным образом выстраиваться в поле стоячей волны, приводя, таким образом, к локальным изменениям оптического коэффициента отражения суспензии, которые зависят от локальных значений амплитуды звука [27].
3.8. ИЗМЕРЕНИЕ БИОЛОГИЧЕСКИ ЭФФЕКТИВНЫХ ЭКСПОЗИЦИЙ И ДОЗ
Другая важная область, в которой возникает необходимость измерения параметров акустических полей, связана с исследованием изменений, вызываемых ультразвуком в живых клетках и тканях, с практическими вопросами безопасности диагностического применения ультразвука и эффективности его терапевтического использования. Биологические и прикладные аспекты этой проблемы детально обсуждаются в гл. 12—14, но было бы полезным рассмотреть здесь ситуацию в отношении физических измерений.
По прочтении этих глав станет ясным, что ультразвук, производя какие-либо наблюдаемые эффекты, может вызывать изменения в живых клетках и тканях посредством большого числа различных механизмов, причем каждый из них по-своему зависит от условий облучения. Будет также показано, что некоторые механизмы изучены еще недостаточно и что взаимосвязь условий облучения с наблюдаемыми эффектами если и известна, то очень приблизительно. Следовательно, в настоящее время еще нет возможности разработать обоснованную и универсальную систему «ультразвуковой дозиметрии».
Существует важное, но не всегда должным образом оцениваемое отличие ультразвуковой дозиметрии от дозиметрии ионизирующего излучения, где установлено, что величина поглощенной энергии на единицу массы позволяет количественно предсказать как терапевтическую эффективность, так и ожидаемые повреждения. За исключением некоторых очень специфических ситуаций, не существует эквивалентного параметра для предсказания ультразвуковых эффектов.
Ввиду отсутствия для ультразвука единой удовлетворительной дозиметрической величины единственным разумным способом количественного описания условий экспериментального воздействия, позволяющим проводить сравнение результатов и предсказывать наиболее важные последствия, является приведение полных пространственных и временных характеристик используемого акустического поля. В большинстве случаев наиболее удовлетворительно такие измерения осуществляются с помощью пьезоэлектрических гидрофонов, описанных выше в разд. 3.2.
Современная практика, которая исходит из традиционного представления о том, что простые радиометрические весы — наиболее удобный измерительный прибор, базируется на понятиях «интенсивность», или, что, возможно, более точно, «экспозиционная интенсивность» (мощность, проходящая через единицу площади используемой апертуры, обычно измеряемая в Вт/см2). Интенсивность обычно подразделяется в зависимости от того, используется ли она для выражения пиковой величины или средней, которая в свою очередь подразделяется на среднюю по пространству, т. е. по используемой апертуре, и среднюю по времени, т. е. по определенному времени экспозиции.
Таким образом, на практике используются
интенсивность SATA — средняя по пространству, средняя по времени,
интенсивность SATP — средняя по пространству, пиковая по времени,
интенсивность SPTP — пиковая по пространству, пиковая по времени,
интенсивность SPTA — пиковая по пространству, средняя по времени1).
Очевидно, что длительность импульсов и частота их повторения достаточно важны при изучении биологических эффектов, и поэтому они должны документироваться так же, как и частота ультразвука или спектральный состав в случае облучения широкополосным сигналом или короткими импульсами.
И все же в некоторых практических ситуациях возникает необходимость охарактеризовать излучение ультразвука аппаратурой или экспозицию живой ткани каким-либо одним числом. В публикации Всемирной организации здравоохранения [13] в этих случаях рекомендуется использовать следующие параметры:
1) для излучений и экспозиций в эхо-импульсных диагностических приборах — пиковую по пространству амплитуду давления (в паскалях);
1) В сокращенных обозначениях используются первые буквы следующих английских слов: S — spatial (пространственный), Т — temporal (временной), А — average (средний), Р — peak (пиковый). — Прим. перев.
2) для терапевтических, хирургических и доплеровских диагностических приборов (импульсных и на непрерывных волнах) — основную мощность пучка (в ваттах), которая определяется как 0,541 от произведения пиковой по пространству средней по времени интенсивности (Вт/см2) на площадь сечения пучка по уровню 6 дБ (см2). Множитель 0,541 выводится математически из предположений об аксиальной симметрии пучка с гауссовским профилем и о линейном распространении гармонической волны.
Логика такого подхода основывается на рассмотрении биофизических механизмов воздействия, наиболее вероятных в данной ситуации, и будет обоснована в гл. 12—14. То, что эхо-импульсные экспозиции приведут к заметным нагревам, кажется маловероятным; если они и вызовут какой-либо эффект, то скорее всего он будет связан с механическим воздействием, пригодной мерой для которого является амплитуда давления. В противоположность этому источники ультразвука, указанные выше во втором пункте, как известно, способны оказывать скорее термическое, чем механическое воздействие, и поэтому величина мощности, особенно той ее части, что сконцентрирована в центре пучка, вероятно, наиболее полно характеризует воздействие.
В вышеприведенном обсуждении использовались два термина: «доза» и «экспозиция». Хотя, по-видимому, не существует универсального подхода, но по аналогии с ионизирующим излучением предполагается, что экспозиция характеризует энергию или интенсивность пучка, падающего на мишень. В то же время доза указывает на энергию, преобразованную внутри мишени в биологически эффективную форму (важным, но не единственным примером которой может служить тепло). В большинстве акустических измерений регистрируется экспозиция, а не доза, и, несмотря на некоторую нескладность, предпочтительней было бы пользоваться термином «экспозиметрия», а не «дозиметрия» [16].
1. Anson, L. W. & Chivers, R. С. (1980) The use of absorbing polymeric materials for suspended sphere ultrasonic radiometers. Acoustics Letters 4, 74—80.
2. Bobber, R. J. (1978) Underwater acoustic measurements. Washington D. C, Naval Research Lab.
3. Borgnis, E (1953) Acoustic radiation pressure of plane compressional waves. Rev. Mod. Phys. 25, 653—664.
4. Breazeale, M. A. & Heldermann, E. A. (1959) Optical methods for the measurement of the sound pressure in liquids. J. acoust. Soc. Amer. 31, 24—28.
5. Busse, L. J. & Miller, J. G. (1981a) Response characteristics of a finite aperture phase insensitive ultrasonic receiver based on the acoustoelectric effect. J. acoust. Soc. Amer. 70, 1370—76.
6. Busse, L. J. & Miller, J. G. (1981b) Detection of spatially non-uniform ultrasonic radiation with phase sensitive (piezoelectric) and phase insensitive (acoustoelectric) receivers. /. acoust. Soc. Amer. 70, 1377—1386.
7. Durr, W., Sinclair, D. A. & Ach, E. A. (1980) High resolution acoustic probe. Electronics Letters 16, 805—806.
8. Erikson, K. R. (1972) Calibration of standard ultrasonic probe transducers using light diffraction, in Interaction of ultrasound and biological tissues: workshop proceedings (eds. J. M. Reid & M. Sikov) pp. 193—197. DHEW Publication (FDA) 73—8003, BRH/DBE 73—1, U.S. Govt. Printing Office, Washington D. C.
9. Farmery, M. J. & Whittingham, T. A. (1978) A portable radiation-force balance for use with diagnostic ultrasonic equipment. Ultrasound in Med. and Biol. 4, 273—279.
10. Filipczynski, L. S. (1969) Absolute measurement of particle velocity, displacement, or intensity of ultrasonic pulses in liquids and solids. Acustica, 3, 137.
11. Foldy, L. L. & Primakoff (1945; 1947) A general theory of passive linear electroacoustic transducers, and electrocoustic reciprocity theorem. J. acoust. Soc. Amer. 17, 109 and 19, 50.
12. Fry, W. J. & Fry, R. B. (1954) Determination of absolute sound levels and acoustic absorption coefficients by thermocouple probes — theory and experiment. J. acoust. Soc. Amer. 26, 294—310 and 311—317.
13. ter Haar, G. R. & Hill C. R. (в печати).
14. Hasegawa, Т. & Yosioka, К. (1969) Acoustic radiation force on a solid elastic sphere. J. acoust. Soc. Amer. 46, 1139—1143.
15. Hill, C. R. (1970) Calibration of ultrasonic beams for biomedical applications. Phys. Med. Biol. 15, 241—248.
16. Hill, C. R. (1975) A proposed facility for ultrasound exposimetry and calibration. Ultrasound in Med. and Biol. 1, 476.
17. IEC (198—) The characteristics and calibration of hydrophones for operation in the frequency range 0.5 MHz to 15 MHz, IEC Report No. —, International Electrotechnical Commission Geneva (в печати).
18. Klein, W. R. & Cook, B. D. (1967) Unified approach to ultrasonic light diffraction. IEEE Trans. SU 14, 123—134.
19. Laughlin, J. S. & Genna, S. (1966) Calorimetry, Radiation dosimetry Vol. 2. (ed. F. H. Attix & W. C. Roesch). pp. 389—441. Academic Press, New York.
20. Lewin, P. A. (1981) Miniature piezoelectric polymer ultrasonic hydrophones probes. Ultrasonics 19, 213—216.
21. Lewin. P. A. & Chivers, R. C. (1981) Two miniature ceramic ultrasonic probes. J. Phys. E. Sci. Instrum. 14, 1420—1424.
22. Livett, A. J., Emery, E. W. & Leeman, S. (1981) Acoustic radiation pressure. J. Sound and Vibration 76, 1—11.
23. McLean, W. R. (1940) Absolute measurement of sound without a primary standard. J. acoust. Soc. Amer. 12, 140.
24. Mezrich, R. S., Etzoid, K. F. & Vilkomerson, D. H. R. (1975) System for visualizing and measuring ultrasonic wavefronts, in Acoustical Holography Vol. 6 (ed. N. Booth) pp. 165—191. Plenum Press, New York.
25. Miller, E. B. & Eitzen, D. G. (1979) Ultrasonic transducer characterization at the NBC. IEEE Trans. SU 26, 28—37.
26. O'Brien, W. D. (1978) Ultrasonic dosimetry, Ultrasound: its application in medicine and biology Part I, (ed, F. J. Fry) pp. 343—391. Elsevier, Amsterdam. 4
27. Pohlmann, R. (1948) Materialdurchleuchtung mittels Schalloptischen Abbildungen, i Zeits fur Angewandte Physik 1, 181—187.
28. Reibold, R. (1977) Application of holographic interferometry for the investigation & of ultrasonic fields. Acustica 38, 253—257.
29. Reid, S. M. & Sikov, M. R. (1973) Interaction of ultrasound and biological tissues — Section 4: Ultrasound dosimetry, pp. 153—201 (various authors), DHEW Publication (FDA) 73—8008, U. S. Govt. Printing Office, Washington D. C.
30. Riley, W. A. & Klein. W. R. (1967) Piezo-optic coefficients of liquids. J. acoust. Soc. Amer. 42, 1258—1261.
31. Rooney, J. A. (1973) Determination of acoustic power outputs in the microwatt-milliwatt range. Ultrasound in Med. and Biol. 1, 13—16.
32. Rooney, J. A. & Nyborg, W. L. (1972) Acoustic radiation pressure in a travelling plane wave. Amer. J. Phys. 40, 1825—1830.
33. Schombert, D. G., Smith, S. W. & Harris, G. R. (1982) Angular response of minature ultrasonic hydrophones. Med. Phys. 9, 484—492.
34. Shotton, К. C. (1980) A tethered float radiometer for measuring the output power from ultrasonic therapy equipment. Ultrasound in Med. and Biol. 6, 131—133.
35. Shotton, К. C, Bacon, D. R. & Quilliam, R. M. (1980) A PVDF membrane hydrophone for operation in the range 0.5 MHz to 15 MHz. Ultrasonics 18, 123—126.
36. Stockdale, H. R. & Hill, C. R. (1976) Use of sphere radiometer to measure ultrasonic beam power. Ultrasound in Med. and Biol. 2, 219—220.
37. Torr, G. R. & Watmough, D. J. (1977) A constant-flow calorimeter for the measurement of acoustic power at megahertz frequencies. Phys. Med. Biol. 22, 444—450.
38. Weinreich, G., Sanders, Т. M. & White, H. G. (1959) Acoustoelectric effect in n-type germanium. Phys. Rev. 114, 33—44.
39. Wells, P. N. Т., Bullen, M. A., Follett, D. H., Freundlich, H. F. & Angell-James, J. (1978) The dosimetry of small ultrasonic beams. Ultrasonics 1, 106—110.
40. Sarvazyan, A. P., Pashovkin, T. N. & Shilnikov, G. V. (1985) An extremely simple and rapid method for registration of ultrasonic field patterns. Proc. of Ultrasonics Int. 1985 (London), 324—328.
ЗАТУХАНИЕ И ПОГЛОЩЕНИЕ УЛЬТРАЗВУКА
Дж. Бэмбер
Как уже отмечалось в гл. 1, характер распространения ультразвуковой волны определяется инерционными и упругими свойствами среды, а также действующими в ней механизмами потерь. Плотность и сжимаемость среды определяют скорость звука, пространственные изменения которой приводят к рефракции акустических волн. Пространственные флуктуации либо плотности, либо сжимаемости (совместно эти величины определяют удельный акустический импеданс), либо поглощения звука вызывают рассеяние или отражение волн. Затухание, т. е. полные потери акустической энергии в биологической ткани, определяется суммарным действием рефракции, отражения, рассеяния и поглощения ультразвука.
В практических приложениях данные об изменении скорости, акустического импеданса, поглощения, рассеяния и затухания в объеме ткани используются для получения информации о ее структуре. В частности, все эти параметры вносят вклад в сложный процесс формирования эхо-импульсных изображений и влияют на внешний вид этих изображений. Отсюда следует, что знание этих параметров, а также их зависимости от частоты, амплитуды, температуры, возраста пациента, той или иной патологии необходимо для анализа возможностей и наиболее эффективного использования существующей и разрабатываемой ультразвуковой диагностической аппаратуры. Коэффициенты затухания и поглощения определяют также величину акустической мощности, достигшей заданного участка ткани и выделившейся в виде тепла. Другими словами, эти параметры играют важную роль при анализе характера и эффективности биологического действия ультразвука, о чем пойдет речь в гл. 12—14.
Затухание звуковой волны за счет действия любого из указанных выше механизмов потерь приводит к появлению в уравнении (1.33) из гл. 1 дополнительного постоянного множителя а, приведенного к единичной длине пути. В результате для плоской волны, распространяющейся в положительном направлении оси х, можно записать
![]()
В реальных ситуациях редко приходится иметь дело с идеальными плоскими волнами, поэтому помимо указанных механизмов потерь почти всегда имеют место дополнительные потери (или приращения) интенсивности звука, связанные с перераспределением энергии в дифракционном поле источника (см. гл. 1 и 2). Потери акустической энергии, обусловленные дифракцией и называемые дифракционными потерями, могут приводить к погрешности результатов измерения затухания или рассеяния в биологической ткани. Кроме того, связанные с дифракцией изменения фазовых соотношений также приводят к погрешности при измерениях скорости звука. При обработке экспериментальных данных можно учесть влияние этих погрешностей на результаты измерений, вводя так называемые дифракционные поправки.
Если отражение и рефракцию в объеме среды рассматривать как частные случаи более общего явления рассеяния, то можно отметить, что теория распространения акустических волн в биологических средах развивалась по двум достаточно самостоятельным направлениям. С одной стороны, исследовались поглощение и дисперсия акустических волн, с другой — их рассеяние. Специфические особенности теории рассеяния будут рассмотрены в гл. 6, хотя, как будет показано в дальнейшем (см. разд. 4.3.7), не всегда достаточно просто провести различие между явлениями рассеяния и поглощения. В данной главе представлен подробный анализ явлений затухания, поглощения и дисперсии звука, а также рассмотрены методы измерения затухания. Гл. 5 посвящена методам измерения скорости звука.
4.2. СЕЧЕНИЯ ВЗАИМОДЕЙСТВИЯ УЛЬТРАЗВУКОВОЙ ВОЛНЫ С БИОЛОГИЧЕСКОЙ ТКАНЬЮ
В различных областях физики, имеющих дело с взаимодействием волнового излучения с веществом, для количественной оценки поглощения и рассеяния обычно используются соответствующие сечения взаимодействия для отдельных частиц среды, на которые падает волна. Применительно к биологическим тканям провести численный расчет единичных сечений взаимодействия, вообще говоря, невозможно, и возникает необходимость в использовании параметров, характеризующих объемные рассеивающие и поглощающие свойства таких тканей. Этими параметрами являются макроскопические сечения или сечения взаимодействия, относящиеся к единице объема рассматриваемой ткани. В частности, используются три такие величины, отнесенные к единичному объему среды — сечения затухания, поглощения и рассеяния. Чтобы выявить физический смысл этих параметров и показать, каким образом они могут быть связаны с единичными сечениями взаимодействия, мы рассмотрим среду, состоящую из локальных неоднородностей двух типов, одни из которых поглощают, а другие рассеивают акустическую энергию. Пусть в единичном объеме среды имеется щ рассеивающих неоднородностей, каждая из которых характеризуется элементарным сечением рассеяния ![]() , и
, и ![]() поглощающих неоднородностей с элементарным сечением поглощения
поглощающих неоднородностей с элементарным сечением поглощения ![]() . Эти элементарные сечения определяются как отношение полной мощности, поглощенной или рассеянной данной неоднородностью, к интенсивности падающей волны. Они имеют размерность площади и численно равны площади поперечного сечения падающей плоской волны, мощность которой равна либо рассеянной, либо поглощенной мощности. Если падающий пучок имеет приблизительно постоянную площадь поперечного сечения S, полную мощность W и равномерное распределение интенсивности по сечению, то мощность, рассеянная одной локальной неоднородностью, будет равна
. Эти элементарные сечения определяются как отношение полной мощности, поглощенной или рассеянной данной неоднородностью, к интенсивности падающей волны. Они имеют размерность площади и численно равны площади поперечного сечения падающей плоской волны, мощность которой равна либо рассеянной, либо поглощенной мощности. Если падающий пучок имеет приблизительно постоянную площадь поперечного сечения S, полную мощность W и равномерное распределение интенсивности по сечению, то мощность, рассеянная одной локальной неоднородностью, будет равна ![]() , а мощность, поглощенная одной неоднородностью, —
, а мощность, поглощенная одной неоднородностью, — ![]() . Отсюда мощности, рассеянные и поглощенные в единичном объеме, будут соответственно определяться как.
. Отсюда мощности, рассеянные и поглощенные в единичном объеме, будут соответственно определяться как.
![]()
Величины ![]() можно рассматривать (при отсутствии многократного рассеяния) как сечение рассеяния (
можно рассматривать (при отсутствии многократного рассеяния) как сечение рассеяния (![]() и сечение поглощения № единичного объема среды.
и сечение поглощения № единичного объема среды.
Величины рассеянной и поглощенной мощности на единичной длине пути будут равны соответственно ![]() и
и ![]() Следовательно, в случае тонкой мишени толщиной
Следовательно, в случае тонкой мишени толщиной ![]() полная рассеянная мощность будет определяться как
полная рассеянная мощность будет определяться как
![]()
тогда как полная поглощенная мощность будет равна
![]()
В сумме величины ![]() и
и ![]() дают полную мощность, характеризующую взаимодействие волны со средой
дают полную мощность, характеризующую взаимодействие волны со средой
![]()
Величина ![]() представляет собой полное сечение взаимодействия (или затухания), отнесенное к единичному объему среды. В дальнейшем она будет обозначаться символом д.
представляет собой полное сечение взаимодействия (или затухания), отнесенное к единичному объему среды. В дальнейшем она будет обозначаться символом д.
В случае мишени конечной толщины уравнение (4.2в) интегрируется. Полагая, что при х = 0 W = W0 (W0 — мощность падающей волны), мы получаем
![]()
Таким образом, мощность является экспоненциально спадающей функцией пройденного пути, причем коэффициент затухания равен полному сечению затухания единичного объема ![]() . Для описания объемных свойств среды справедливы следующие соотношения:
. Для описания объемных свойств среды справедливы следующие соотношения:
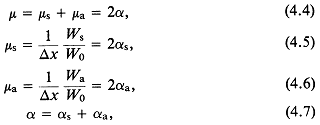
где ![]() — коэффициент затухания по амплитуде,
— коэффициент затухания по амплитуде, ![]() рассеяния по амплитуде (равный коэффициенту затухания при отсутствии поглощения),
рассеяния по амплитуде (равный коэффициенту затухания при отсутствии поглощения), ![]() — коэффициент поглощения по амплитуде (равный коэффициенту затухания при отсутствии рассеяния). К величинам
— коэффициент поглощения по амплитуде (равный коэффициенту затухания при отсутствии рассеяния). К величинам ![]() и
и ![]() одинаково обоснованно применимы термины «макроскопическое сечение», «сечение на единицу объема» и «коэффициент по интенсивности». Единицы, в которых выражаются параметры
одинаково обоснованно применимы термины «макроскопическое сечение», «сечение на единицу объема» и «коэффициент по интенсивности». Единицы, в которых выражаются параметры ![]() и
и ![]() , могут быть различными в зависимости от конкретного применения и цели измерений. При исследовании фундаментальных механизмов взаимодействия акустических волн со средой обычно используются единицы см-1. Эти единицы также называются «непер на сантиметр», поскольку, взяв натуральный логарифм, например, от выражения (4.3), мы можем получить уравнение вида
, могут быть различными в зависимости от конкретного применения и цели измерений. При исследовании фундаментальных механизмов взаимодействия акустических волн со средой обычно используются единицы см-1. Эти единицы также называются «непер на сантиметр», поскольку, взяв натуральный логарифм, например, от выражения (4.3), мы можем получить уравнение вида
![]()
Во многих практических случаях, например при использовании аппаратуры для ультразвуковой визуализации, более удобно выражать отношение W/W0 или соответствующее отношение амплитуд сигналов Р/Ро в дБ. При этом
![]()
и
![]()
причем ![]() и
и ![]() численно равны друг другу и выражаются в единицах дБ/см. Какой-либо коэффициент, выраженный в дБ/см, будет поэтому определяться как произведение множителя l0 lge (= 4,343) на соответствующий коэффициент по интенсивности (в непер/см), или произведение множителя 20 lge (= 8,686) на соответствующий коэффициент по амплитуде.
численно равны друг другу и выражаются в единицах дБ/см. Какой-либо коэффициент, выраженный в дБ/см, будет поэтому определяться как произведение множителя l0 lge (= 4,343) на соответствующий коэффициент по интенсивности (в непер/см), или произведение множителя 20 lge (= 8,686) на соответствующий коэффициент по амплитуде.
При анализе механизмов поглощения часто используется величина, называемая удельным поглощением. Она равна коэффициенту поглощения, деленному на плотность среды, или в случае вещества в растворе так называемому коэффициенту «избыточного» поглощения (араствор — арастворитель), деленному на весовую концентрацию растворенного вещества. Аналогичным образом, биологические ткани можно характеризовать удельным коэффициентом затухания. При вычислении избыточного затухания обычно предполагается, что биологические ткани представляют собой суспензию, в которой «растворителем» является вода. Коэффициенты удельного поглощения и затухания имеют размерность непер (или децибел) на см2 на грамм и используются для облегчения сравнения свойств различных материалов по затуханию и поглощению независимо от плотности или концентрации. Относительной величиной, которая часто используется при анализе поглощения ультразвука в растворах, является сечение молекулярного поглощения. Известная также под названием «избыточное поглощение на молекулу», эта величина определяется как коэффициент избыточного поглощения, деленный на число молекул растворенного вещества в единичном объеме растворителя (это число равно произведению молярной концентрации на число Авогадро). Отметим, что в дальнейшем при анализе механизмов поглощения звука (разд. 4.3.1) мы будем использовать термин «избыточное поглощение», определение которого отличается от представленного здесь понятия. В литературе этот термин не имеет однозначного значения — существует два совершенно различных его определения, которые не следует путать.
И наконец, остается отметить последний, но весьма важный момент. В строгом смысле коэффициент затухания, определяемый формулами (4.3) и (4.4), является теоретически идеализированным параметром, который на практике не может быть измерен прямым путем. В соответствии с этим величина ![]() фактически никогда не будет давать истинного представления о наблюдаемом пропорциональном уменьшении мощности в реальных экспериментах. Дело в том, что всегда будет существовать некоторая часть
фактически никогда не будет давать истинного представления о наблюдаемом пропорциональном уменьшении мощности в реальных экспериментах. Дело в том, что всегда будет существовать некоторая часть ![]() s (соответствующая рассеянию в прямом направлении), дающая определенный вклад в мощность принимаемого сигнала на расстоянии x. Фактически можно рассмотреть две совершенно разные схемы измерения коэффициента затухания. В одной из них используется «идеальная» конфигурация, при которой приемная апертура либо имеет бесконечно малые размеры, либо находится на бесконечно большом расстоянии от исследуемой точки. При этом рассеянные сигналы не регистрируются, и измеренной величиной действительно является параметр
s (соответствующая рассеянию в прямом направлении), дающая определенный вклад в мощность принимаемого сигнала на расстоянии x. Фактически можно рассмотреть две совершенно разные схемы измерения коэффициента затухания. В одной из них используется «идеальная» конфигурация, при которой приемная апертура либо имеет бесконечно малые размеры, либо находится на бесконечно большом расстоянии от исследуемой точки. При этом рассеянные сигналы не регистрируются, и измеренной величиной действительно является параметр ![]() . Согласно другой, полностью «неидеальной» схеме, приемник должен иметь настолько большие размеры, чтобы целиком охватить исследуемый образец и зарегистрировать все рассеянные волны. При этом измеряемой величиной становится коэффициент поглощения
. Согласно другой, полностью «неидеальной» схеме, приемник должен иметь настолько большие размеры, чтобы целиком охватить исследуемый образец и зарегистрировать все рассеянные волны. При этом измеряемой величиной становится коэффициент поглощения ![]() a В реальных ситуациях любые схемы измерения не являются идеальными и в зависимости от конкретной конфигурации должны давать заниженные значения коэффициента затухания. Однако, как будет показано в разд. 4.4, существует множество других причин, приводящих к тому, что значительно чаще измеренные значения коэффициентов затухания оказываются завышенными. В задачах дозиметрии и ультразвуковой визуализации такие понятия, как «точное» измерение, а также измеренное значение коэффициента затухания, приобретают смысл только при детальном описании конкретной схемы измерения.
a В реальных ситуациях любые схемы измерения не являются идеальными и в зависимости от конкретной конфигурации должны давать заниженные значения коэффициента затухания. Однако, как будет показано в разд. 4.4, существует множество других причин, приводящих к тому, что значительно чаще измеренные значения коэффициентов затухания оказываются завышенными. В задачах дозиметрии и ультразвуковой визуализации такие понятия, как «точное» измерение, а также измеренное значение коэффициента затухания, приобретают смысл только при детальном описании конкретной схемы измерения.
4.3. АНАЛИЗ МЕХАНИЗМОВ ПОГЛОЩЕНИЯ ПРОДОЛЬНЫХ УЛЬТРАЗВУКОВЫХ ВОЛН
Вопросам поглощения и дисперсии ультразвука в биологических средах посвящен целый ряд обстоятельных обзорных работ. Среди них следует выделить работы Карстенсена [30], Данна и др. [53], Данна и О'Брайена [56], Фрая и Данна [75], Джонстона и др. [107], Уэллса [203] и Вудкока [207]. Однако основные теоретические положения, хотя они и не касались непосредственно биологических сред, были разработаны еще до появления этих обзоров (см., например, работы Маркхема и др. [143], Герцфельда и Литовица [97]). Заслу живает также упоминания монография Матесона [145] 1). Приведенный в данной главе анализ во многом базируется на указанной литературе и содержит лишь важнейшие положения теории. В попытке достичь возможно более современного представления в анализ также включено несколько работ последних лет.
4.3.1. ОДНОРОДНЫЕ ВОДОПОДОБНЫЕ СРЕДЫ
Поглощение энергии акустической волны приводит к ее необратимому преобразованию в тепло. Это происходит, если периодические изменения плотности среды не совпадают по фазе с колебаниями звукового давления. Применительно к «однородным» средам (например, в растворах макромолекул) известно, что механизмы, ответственные за подобное преобразование энергии, являются релаксационными. Следует отметить, что даже в случае самых простых сред нет полного понимания действия этих механизмов, хотя установлено, что они возникают в результате временного запаздывания в нарушении физического или химического равновесия под действием периодических изменений параметров волны. Можно считать, что в произвольный момент времени полная энергия волны распределена по различным формам энергии, к которым относятся энергия поступательного движения, колебательная энергия и энергия структурной перестройки молекул, колебательные и структурные состояния кристаллической решетки. С течением времени происходит перераспределение энергии, причем оно происходит с конечной скоростью, определяемой процессами обмена, присущими данной среде. Процессы обмена энергией сами по себе представляют определенные механизмы поглощения, тип и число которых могут существенно меняться при переходе от одной жидкости к другой.
Общее выражение, характеризующее поглощение звука на частоте f (длина волны ![]() ) при одиночном процессе релаксации, имеет вид
) при одиночном процессе релаксации, имеет вид
![]()
где ![]() — константа (иногда называемая амплитудой релаксации), определяемая максимальным значением произведения длины волны на коэффициент поглощения или поглощения за период
— константа (иногда называемая амплитудой релаксации), определяемая максимальным значением произведения длины волны на коэффициент поглощения или поглощения за период ![]() , скоростью звука с и частотой релаксации fR.
, скоростью звука с и частотой релаксации fR.
1)Основные теоретические вопросы, касающиеся механизмов поглощения ультразвука в жидких средах, наиболее полно рассмотрены в монографии: Михайлов И.Г., Соловьев В.А., Сырников Ю.П. Основы молекулярной акустики. — М.: Наука, 1964. — Прим. ред.
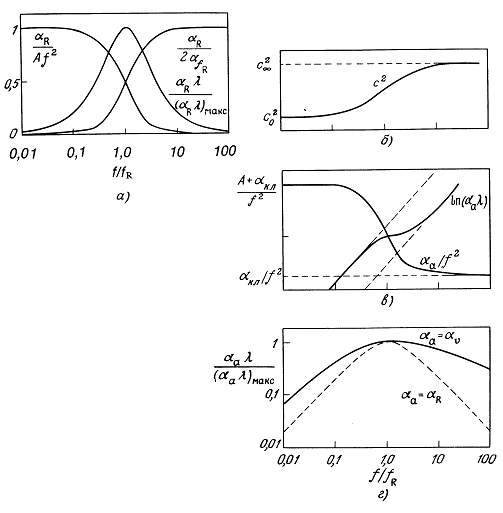
Рис. 4.1. Поглощение (а) и дисперсия скорости звука (б) в случае одиночного релаксационного процесса с постоянной времени ![]() ; в — поглощение звука в случае комбинированного действия одиночного релаксационного процесса и процессов классического поглощения; r — сравнительное действие процесса вязкого относительного движения и релаксационного процесса.
; в — поглощение звука в случае комбинированного действия одиночного релаксационного процесса и процессов классического поглощения; r — сравнительное действие процесса вязкого относительного движения и релаксационного процесса.
Рис. 4.1, а помогает понять смысл этого уравнения. На низких частотах параметры волны изменяются достаточно медленно, так что процесс перераспределения энергии почти не нарушается, и энергия других видов передается обратно в волну лишь с незначительным отклонением по фазе, при этом поглощение мало. По мере повышения частоты обратная передача энергии сопровождается все возрастающим отклонением по фазе от фазы волны.
1) Эту величину часто неправильно называют поглощением на длину волны.
Поглощение растет до тех пор, пока на частотах, намного превышающих частоту релаксации, акустическая волна в силу малости временных интервалов уже перестает полностью нарушать термодинамическое равновесие среды, и наблюдается лишь незначительная передача энергии поступательного движения волны во внутренние степени свободы. Произведение длины волны на коэффициент поглощения достигает максимума при f = fR.
При анализе экспериментально полученных зависимостей поглощения от частоты необходимо учитывать целый ряд релаксационных процессов, вклад которых суммируется и добавляется к так называемому коэффициенту классического поглощения, вычисленному Стоксом и Кирхгофом более ста лет назад. Этот результат записывается в виде выражения
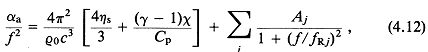
где ![]() — коэффициент сдвиговой вязкости, у — отношение удельных теплоемкостей, Ср — теплоемкость при постоянном давлении и
— коэффициент сдвиговой вязкости, у — отношение удельных теплоемкостей, Ср — теплоемкость при постоянном давлении и ![]() — коэффициент теплопроводности. Величину
— коэффициент теплопроводности. Величину ![]() иногда называют независимым от частоты коэффициентом поглощения.
иногда называют независимым от частоты коэффициентом поглощения.
Первый член в квадратных скобках характеризует вклады в поглощение, обусловленные тем, что молекулы среды перестраиваются в различные локальные структуры за конечное время, определяемое сдвиговой вязкостью. Член с теплопроводностью, который обычно пренебрежимо мал (за исключением расплавленных металлов), описывает потери энергии за счет возникновения теплового потока от областей с высоким звуковым давлением к областям с низким давлением. В случае многокомпонентных жидких смесей возникает, вообще говоря, еще один механизм поглощения, заключающийся в диффузии молекул различного типа вдоль градиентов концентрации, образующихся под влиянием звуковой волны. Однако в реальных случаях вклад этого механизма совершенно ничтожен и в уравнении (4.12) он не учитывается. Вообще все эти вклады описываются более точными релаксационными уравнениями, которые для частот, лежащих ниже соответствующих частот релаксации, сводятся к простым квадратичным зависимостям от частоты, характерным для классических механизмов. Поэтому механизмы поглощения часто, хотя и не совсем корректно, разделяются на «классические» и «релаксационные». Недавно на необоснованность такого разделения указывали Сегал и Гринлиф [190], исследовавшие частотные зависимости поглощения ультразвука в жидкостях и биологических тканях (см. разд. 4.5) в рамках модели, целиком базирующейся на анализе фазовых соотношений между акустическим давлением и колебаниями температуры при наличии релаксационного процесса того или иного типа.
В уравнении (4.12) величины ![]() и
и ![]() являются константами для каждого рассматриваемого процесса и одновременно представляют собой функции распределения по частоте и температуре. Вид этих функций при заданной температуре выбирается таким образом, чтобы результирующая зависимость
являются константами для каждого рассматриваемого процесса и одновременно представляют собой функции распределения по частоте и температуре. Вид этих функций при заданной температуре выбирается таким образом, чтобы результирующая зависимость ![]()
![]() была наилучшей аппроксимацией экспериментальных данных. На рис. 4,1, в схематически показана зависимость, определяемая уравнением (4.12), для одного значения у. Отклонение от линейности графика зависимости
была наилучшей аппроксимацией экспериментальных данных. На рис. 4,1, в схематически показана зависимость, определяемая уравнением (4.12), для одного значения у. Отклонение от линейности графика зависимости ![]() от
от ![]() явно свидетельствует о наличии дополнительных механизмов релаксации.
явно свидетельствует о наличии дополнительных механизмов релаксации.
В случае достаточно сложных биологических сред и мягких тканей угловой коэффициент зависимости log ![]() от
от ![]() изменяется в пределах от 1 до 1.4 в частотном диапазоне 1—10 МГц. Для согласования выражения (4.12) с экспериментальными данными необходимо выбрать конкретный вид соответствующей функции распределения. Часто в качестве функции распределения используется так называемое логарифмическое квадратичное «окно», обеспечивающее информацию об интервале энергий активации при действии данных процессов релаксации. Следует отметить, что в случае биологических сред заранее неизвестно, будет ли дискретное число процессов релаксации вносить вклад в суммарное поглощение или же распределение релаксационных частот является непрерывной функцией частоты. В последнем случае необходимо перейти в уравнении (4.12) от суммирования к интегрированию.
изменяется в пределах от 1 до 1.4 в частотном диапазоне 1—10 МГц. Для согласования выражения (4.12) с экспериментальными данными необходимо выбрать конкретный вид соответствующей функции распределения. Часто в качестве функции распределения используется так называемое логарифмическое квадратичное «окно», обеспечивающее информацию об интервале энергий активации при действии данных процессов релаксации. Следует отметить, что в случае биологических сред заранее неизвестно, будет ли дискретное число процессов релаксации вносить вклад в суммарное поглощение или же распределение релаксационных частот является непрерывной функцией частоты. В последнем случае необходимо перейти в уравнении (4.12) от суммирования к интегрированию.
Разность между измеренным коэффициентом поглощения ![]() и классическим коэффициентом поглощения принято называть «избыточным» поглощением (его не следует путать с «избыточным» коэффициентом поглощения, рассмотренным в разд. 4.2). Это избыточное поглощение обусловлено дополнительными релаксационными процессами, связанными с действием объемной или второй вязкости среды
и классическим коэффициентом поглощения принято называть «избыточным» поглощением (его не следует путать с «избыточным» коэффициентом поглощения, рассмотренным в разд. 4.2). Это избыточное поглощение обусловлено дополнительными релаксационными процессами, связанными с действием объемной или второй вязкости среды ![]() . В своих первоначальных работах Стоке полагал, что величина
. В своих первоначальных работах Стоке полагал, что величина ![]() равна нулю (просто в силу того, что не видел способов ее измерения).
равна нулю (просто в силу того, что не видел способов ее измерения).
1) В данном контексте английские термины bulk viscosity и volume viscosity являются синонимами. Однако в разных публикациях можно встретить различное определение этих терминов. Так, например, в работе Матесона [145] термин volume viscosity используется для описания той части bulk viscosity, которая обусловлена структурной релаксацией. Другие авторы называют эту часть структурной вязкостью.
Эта величина входит в классическое выражение (4.12) как добавка к сдвиговой вязкости. Другими словами, в квадратных скобках вместо члена ![]() должна стоять сумма
должна стоять сумма ![]() .
.
Обычно процессы молекулярной релаксации разделяются на два типа — процессы термической и структурной релаксации. Подробное обсуждение причин такого разделения выходит за рамки нашего краткого рассмотрения. Следует отметить, что эти релаксационные механизмы характеризуются важными различиями, например, в отношении зависимости от температуры. Этот вопрос будет рассмотрен в дальнейшем. Структурные механизмы, рассмотренные Литовицем и Девисом [134], включают в себя внутримолекулярные перегруппировки и переходы между различными равновесными состояниями. Эти механизмы преобладают в ассоциированных жидкостях, таких как вода и спирты. Подобные жидкости состоят из полярных молекул и характеризуются кристаллической структурой ближнего порядка. Структурная релаксация возникает в ответ на изменения напряжения (или давления) в акустической волне. Процессы, обусловленные действием сдвиговой вязкости, являются характерными примерами структурной релаксации. Процессы термической релаксации, обсуждавшиеся Лэмбом [125], наблюдаются в слабо ассоциированных либо неассоциированных жидкостях типа бензола или дисульфида углерода, в которых тепловые флуктуации в волне нарушают внутримолекулярное (т. е. химическое) равновесие. Термическими процессами являются внутримолекулярные движения, связанные с поворотной изомерией, а также взаимодействия между поступательными и внутренними колебательными степенями свободы.
В пределах релаксационной области акустического частотного спектра наблюдается также зависимость скорости звука от частоты. Как и в случае одиночного релаксационного процесса, дисперсия скорости характеризуется зависимостью, показанной на рис. 4.1,6. В однородных средах такая дисперсия скорости явно указывает на влияние дополнительной релаксации. В частотной области дисперсии относительное приращение скорости звука и максимум поглощения, обусловленный релаксационным механизмом, приближенно связаны соотношением

На практике максимальное относительное изменение скорости звука составляет менее 1%, поэтому для получения количественных данных требуется проводить очень точные измерения. Следует также отметить, что в области релаксационных частот зависимость с от ![]() является приблизительно линейной.
является приблизительно линейной.
4.3.2. ВЯЗКОУПРУГИЕ СВОЙСТВА КВАЗИТВЕРДЫХ СРЕД
До сих пор в данной главе, как и в гл. 1, подчеркивалась вязкая природа жидкостей. В классическом случае идеально вязкой (ньютоновской) жидкости приложенное напряжение всегда пропорционально скорости изменения результирующей деформации, но не зависит от величины этой деформации, которая может меняться. В противоположность этому идеально упругое твердое тело подчиняется закону Гука, согласно которому напряжение всегда пропорционально деформации и не зависит от первой производной деформации. Все реальные среды характеризуются комбинацией указанных свойств, т. е. напряжение в них зависит как от самой деформации, так и от ее производной по времени (а также от производных деформации более высоких порядков). Поэтому реальные материалы являются по своей природе вязкоупругими. Следует отметить также, что на практике реакция среды на приложенное напряжение является нелинейной. Этот вопрос подробнее рассматривается далее в разд. 4.3, а пока мы по-прежнему будем предполагать наличие линейности.
Наглядно молекулярную картину вязкоупругости можно представить, рассматривая объем жидкости между двумя пластинами, одна из которых фиксирована, а другая колеблется, создавая в среде синусоидальное сдвиговое напряжение. На низких частотах колебаний вся первичная энергия диссипирует в вязком течении различных слоев жидкости относительно друг друга. Такое течение представляет собой направленный дрейф на фоне хаотического теплового движения молекул жидкости. Если частота колебаний напряжения возрастает до высоких значений, при которых диффузия молекул уже не успевает происходить в течение одного периода сдвйговой деформации, то жидкость приобретает сдвиговую жесткость. При этом вместо диссипации энергии в вязком течении наблюдается сохранение энергии в упругой форме. Промежуточная область перехода от вязкого характера поведения среды на низких частотах к упругому характеру на высоких частотах называется областью вязкоупругой релаксации. При этом время вязкоупругой релаксации представляет собой время диффузионного перехода молекул жидкости.
На низких частотах изменения объема среды происходят синфазно с изменением приложенного давления за счет перемещения молекул между областями с высокой и низкой плотностью. На высоких частотах структура жидкости уже не в состоянии достаточно быстро реагировать на изменения давления, при этом с ростом частоты возникает объемная или структурная релаксация. В этом случае время релаксации определяется временем, необходимым для перехода жидкости к новому равновесному объему вслед за быстрым изменением приложенного давления.
Продольная ультразвуковая волна характеризуется как сдвиговой компонентой, так и компонентой сжатия, поэтому в общем случае ее распространение можно описать с помощью модуля сдвига, объемного модуля упругости и времен релаксации.
По существу теория вязкоупругости является феноменологической и ее можно использовать для описания механических свойств любых макроскопически однородных твердых и жидких сред. Эта теория не рассматривает в явном виде процессы, происходящие на молекулярном уровне, но может включать в себя анализ механизмов сдвиговой и объемной релаксации, о которых шла речь в разд. 3.1. Теория вязкоупругости [36] нашла наибольшее применение при анализе механических свойств различных полимеров [62, 145], находящихся как в твердой фазе, так и в растворе. Полимеры являются характерными представителями вязкоупругих материалов, занимающих по своим свойствам промежуточное положение между жидкостями и твердыми средами. В большинстве работ по применению ультразвука в медицине и биологии анализу вязкоупругих свойств уделялось мало внимания. Однако буквально с самых первых экспериментов по измерению поглощения в биологических тканях исследователи предполагали, что теория вязкоупругости к этим средам может быть также применена [104]. Ниже приводится краткое изложение некоторых аспектов теории вязкоупругости, цель которого — дать представление о сути работ, опубликованных по данной тематике. Выводы теории даются без строгого математического доказательства и служат только для иллюстрации результатов, опубликованных в литературе.
Отметим прежде всего, что уравнение (4.1) можно представить в виде

Это уравнение вновь можно привести к виду ![]() введя комплексную величину скорости звука с, определяемую как
введя комплексную величину скорости звука с, определяемую как
![]()
В этом выражении величина ![]() представляет собой фазовую скорость при отсутствии в среде затухания. При наличии затухания фазовая скорость становится комплексной и зависит от частоты, т. е. существует дисперсия скорости.
представляет собой фазовую скорость при отсутствии в среде затухания. При наличии затухания фазовая скорость становится комплексной и зависит от частоты, т. е. существует дисперсия скорости.
Одномерное волновое уравнение, описывающее распространение звуковых волн в твердых телах, имеет вид
![]()
где ![]() — модуль упругости для одноосной деформации, К— модуль всестороннего сжатия и G — модуль сдвига. Аналогичные уравнения можно написать для чисто продольных или сдвиговых волн, если модуль упругости М заменить соответственно модулем К или G. Из волнового уравнения скорость распространения звуковых волн в твердых телах определяется следующим образом:
— модуль упругости для одноосной деформации, К— модуль всестороннего сжатия и G — модуль сдвига. Аналогичные уравнения можно написать для чисто продольных или сдвиговых волн, если модуль упругости М заменить соответственно модулем К или G. Из волнового уравнения скорость распространения звуковых волн в твердых телах определяется следующим образом:
![]()
Отсюда следует, что модуль М также должен быть комплексным и должен зависеть от частоты. Это справедливо и для модулей К и G. Поэтому в общем случае мы можем написать
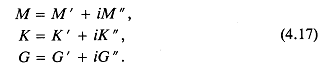
Действительные части этих комплексных выражений представляют собой модули упругости, каждый из которых находится в фазе с гармонически изменяющейся деформацией, тогда как мнимые части — это модули потерь, сдвинутые по фазе на 90° относительно деформации.
Подстановка (4.14) в (4.16) позволяет выразить действительную и мнимую части величины М через параметры ![]() и
и ![]() . Если потери достаточно малы и выполняется условие
. Если потери достаточно малы и выполняется условие ![]() , то в результате такой подстановки можно получить
, то в результате такой подстановки можно получить
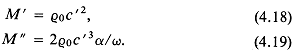
В большинстве работ, посвященных анализу вязкоупругих свойств материалов, экспериментальные данные выражаются через модули М' и М", либо через модули, соответствующие неодноосным деформациям. Выражения (4.18) и (4.19) позволяют достаточно быстро проанализировать результаты измерений и связать их с часто используемыми в медицинской акустике параметрами — скоростью звука и коэффициентом затухания, поскольку ![]() и
и ![]() (тангенс угла потерь).
(тангенс угла потерь).
Если через ![]() и
и ![]() обозначить соответственно обобщенные напряжение и деформацию, то модули упругости в случае идеально упругого твердого тела будут определяться выражениями
обозначить соответственно обобщенные напряжение и деформацию, то модули упругости в случае идеально упругого твердого тела будут определяться выражениями ![]() и
и ![]() . Коэффициенты вязкости для ньютоновской жидкости также можно выразить через напряжение и деформацию с помощью соотношений
. Коэффициенты вязкости для ньютоновской жидкости также можно выразить через напряжение и деформацию с помощью соотношений ![]() . Индексы v и s относятся соответственно к объемной и сдвиговой деформации.
. Индексы v и s относятся соответственно к объемной и сдвиговой деформации.
Моделирование вязкоупругих свойств среды на макроскопическом уровне можно осуществить многими способами, используя различные комбинации упругих и вязких элементов. Обычно эти элементы условно называют соответственно пружинами и демпферами. Часто применяются два подобных способа, известные под названиями модели Максвелла и модели Фойгта1). На рис. 4.2, а и б показаны соединения пружин и демпферов, образующие элемент Максвелла и элемент Фойгта. Анализ этих моделей или их эквивалентных электрических цепей2) показывает, что в модели Максвелла приложенное к среде напряжение (электрическое напряжение) действует одинаково на упругий (емкостной) и вязкий (резистивный) элементы, а их деформации или скорости изменения деформации (ток) просто складываются. В модели Фойгта каждый элемент испытывает одинаковую деформацию, а приложенное напряжение есть сумма упругой и вязкой компонент (деление напряжения). Из рис. 4.2 следует, что для модели Максвелла
1) Подробное описание физической сущности этих подходов содержится в монографии И.Г. Михайлова и др. «Основы молекулярной акустики». — Прим. ред.
2) Описание эквивалентных электрических и механических величин можно найти, например, в работе Брэддика [24] на с. 42.
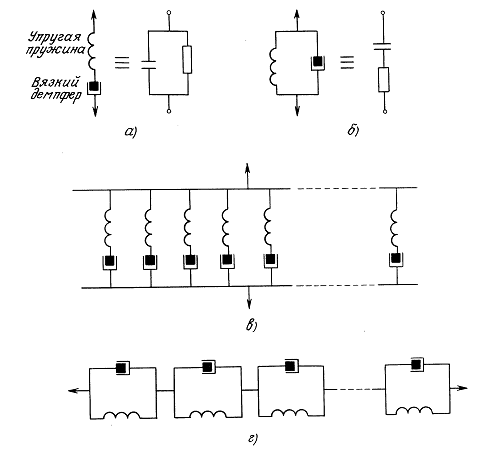
Рис. 4.2. а — Элемент Максвелла и его эквивалентная электрическая схема; б — элемент Фойгта и его эквивалентная электрическая схема; в и г — обобщенные механические модели, построенные соответственно из элементов Максвелла и элементов Фойгта и применяемые для описания макроскопических свойств вязкоупругих материалов [62].
![]()
тогда как для модели Фойгта
![]()
При выводе этих уравнений учитывались только сдвиговые деформации. Величина ![]() соответствует значению модуля упругости в случае, когда среда ведет себя подобно идеальному твердому телу, т. е. при бесконечно больших частотах. Решения уравнений (4.20) и (4.21) можно найти в книгах, посвященных анализу электрических цепей. В частности, переходная характеристика системы, описываемой уравнением (4.21), при мгновенном снятии приложенного напряжения определяется выражением
соответствует значению модуля упругости в случае, когда среда ведет себя подобно идеальному твердому телу, т. е. при бесконечно больших частотах. Решения уравнений (4.20) и (4.21) можно найти в книгах, посвященных анализу электрических цепей. В частности, переходная характеристика системы, описываемой уравнением (4.21), при мгновенном снятии приложенного напряжения определяется выражением
![]()
где ![]() — величина сдвиговой деформации в тот момент времени, когда
— величина сдвиговой деформации в тот момент времени, когда ![]() — постоянная времени или время релаксации для элемента Фойгта. Данная переходная характеристика описывает явление ползучести.
— постоянная времени или время релаксации для элемента Фойгта. Данная переходная характеристика описывает явление ползучести.
Если напряжение изменяется по гармоническому закону, то деформация среды также будет гармонической. При этом зависящие от частоты комплексные модули упругости можно найти, если в уравнениях (4.20) и (4.21) вместо ![]() подставить значение
подставить значение ![]() и производные по времени заменить множителем
и производные по времени заменить множителем ![]() . В результате для элемента Максвелла получаем
. В результате для элемента Максвелла получаем
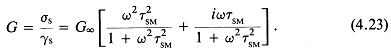
Аналогичным образом для элемента Фогта можно найти, что
![]()
Деформации сжатия можно рассмотреть на основе модели, аналогичной той, которая показана на рис. 4.2, б. В этой модели упругий элемент (пружина) соответствует упругости на нулевой частоте (модулю К0), а вязкий элемент (демпфер) заменяется максвелловским элементом, для которого справедливо модифицированное уравнение (4.20), записанное с учетом деформации сжатия. Другими словами, соотношение между напряжением и деформацией принимает вид
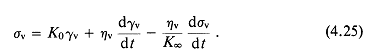
Вводя время объемной релаксации ![]() и предполагая, что изменения объема происходят по гармоническому закону, из выражения (4.25) можно выразить модуль всестороннего сжатия
и предполагая, что изменения объема происходят по гармоническому закону, из выражения (4.25) можно выразить модуль всестороннего сжатия
![]()
В этой формуле величина ![]() представляет собой релаксационную часть модуля всестороннего сжатия.
представляет собой релаксационную часть модуля всестороннего сжатия.
Объединяя уравнение (4.26) либо с уравнением (4.23), либо с уравнением (4.24) и используя (4.16), можно получить выражение для модуля упругости при одноосной деформации М в рамках модели Максвелла или Фойгта. Затем можно использовать уравнения (4.18) и (4.19) для нахождения скорости распространения звука и коэффициента затухания. Подобный вывод приведен в прекрасной работе Рэйчела [185], посвященной сравнительному анализу двух данных моделей. Следует отметить, что времена релаксации ![]() и тв обычно считаются равными друг другу.
и тв обычно считаются равными друг другу.
Как модель Максвелла, так и модель Фойгта позволяют получить дисперсионные соотношения и релаксационные уравнения, аналогичные выражению (4.11). Различие между ними заключается в том, что модель Максвелла предсказывает более сильную дисперсию скорости звука. Кроме того, в рамках модели Максвелла коэффициент затухания с ростом частоты сначала возрастает, а затем выходит на плато (аналогично зависимости, показанной на рис. 4.1, а). Согласно модели Фойгта, затухание неизменно растет при повышении частоты. Другими словами, в случае модели Максвелла величина ![]() спадает до нуля при стремлении частоты к бесконечности, тогда как для модели Фойгта она уменьшается с ростом частоты, достигая некоторого приблизительно постоянного значения на высоких частотах. В последнем случае зависимость поглощения от частоты аналогична кривой, показанной на рис. 4.1, в и характеризующей влияние одиночного равновесного процесса с двумя устойчивыми состояниями, действующего в сочетании с классическими процессами. Различие в оценке дисперсии скорости звука между двумя рассмотренными моделями можно установить, если исследовать уравнения (4.23), (4.24) и (4.26). Можно показать, что в рамках обеих моделей при стремлении частоты со к бесконечности эффективный модуль упругости
спадает до нуля при стремлении частоты к бесконечности, тогда как для модели Фойгта она уменьшается с ростом частоты, достигая некоторого приблизительно постоянного значения на высоких частотах. В последнем случае зависимость поглощения от частоты аналогична кривой, показанной на рис. 4.1, в и характеризующей влияние одиночного равновесного процесса с двумя устойчивыми состояниями, действующего в сочетании с классическими процессами. Различие в оценке дисперсии скорости звука между двумя рассмотренными моделями можно установить, если исследовать уравнения (4.23), (4.24) и (4.26). Можно показать, что в рамках обеих моделей при стремлении частоты со к бесконечности эффективный модуль упругости ![]() стремится к значению
стремится к значению ![]()
![]() . С другой стороны, при
. С другой стороны, при ![]() = 0 в модели Максвелла M0 = К0, а в модели Фойгта
= 0 в модели Максвелла M0 = К0, а в модели Фойгта ![]() .
.
Следует отметить, что для правильного описания экспериментальных данных уравнения (4.24) — (4.26) часто приходится обобщать с учетом конкретных распределений времен релаксации (рйс. 4.2, виг). Было установлено, что теория Максвелла наиболее пригодна для описания распространения звука в жидкостях, тогда как дополнительный учет статического модуля сдвига в модели Фойгта делает эту модель, по-видимому, более подходящей для описания биологических тканей. Последний вывод подтверждается работой [1], автор которой успешно смоделировал биологическую ткань с помощью элемента Фойгта, использовав опубликованные данные по затуханию ультразвука в тканях. При этом он учитывал только одно время релаксации для описания этих данных в диапазоне частот, характерном для медицинских приложений.
При анализе теории вязкоупругости необходимо остановиться еще на одном моменте. Из уравнения (4.19) следует, что

Выражения для модуля М", полученные из уравнений (4.23), (4.24) и (4.26), на низких частотах для обеих моделей приводятся к виду
![]()
где ![]() представляет собой либо
представляет собой либо ![]() , либо
, либо ![]() . Подставляя это выражение в формулу (4.27), получаем следующее выражение, справедливое на низких частотах:
. Подставляя это выражение в формулу (4.27), получаем следующее выражение, справедливое на низких частотах:
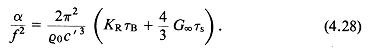
Его можно также представить в виде _ = _2-2
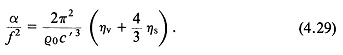
Таким образом, мы снова вернулись к классическому выражению для поглощения в тканях (см. формулу (4.12)).
4.3.3. НЕОДНОРОДНЫЕ СРЕДЫ
Если среда, в которой распространяется звуковая волна, не является однородной жидкостью, то в избыточное поглощение звука могут вносить вклад механизмы, отличные от структурной или тепловой релаксации молекулярных компонент среды. Помимо рассеяния звуковых волн (гл. 6), неоднородности в инерционных или упругих свойствах среды могут быть причиной дополнительных потерь энергии акустических волн за счет вязких или тепловых процессов 1). Если плотность неоднородностей отлична от плотности среды, то в результате относительного движения между частицами взвешенной структуры и средой возникает вязкостное затухание.
1) Другая интерпретация подобных явлений будет рассмотрена в разд. 4.3.7.
Если плотность неоднородностей постоянна, то такие неоднородности будут просто перемещаться взад и вперед вдоль направления распространения акустической волны. Если же плотность неоднородностей различна в разных областях, то существует также тенденция к относительному вращательному движению. В любом случае при уменьшении амплитуды скорости относительного движения в результате действия вязкости среды происходит поглощение энергии акустической волны. Процесс теплового затухания возникает, когда из-за периодических изменений давления в звуковом поле имеет место чередование сжатий и растяжений среды и соответственно идет теплообмен с конечной скоростью между суспендирующей средой и неоднородностью. О'Доннелл и Миллер [166] на основе анализа основных неоднородностей некоторых биологических тканей расчетным путем показали, что в частотном диапазоне 1—10 МГц потери, обусловленные вязким относительным движением, по всей видимости, преобладают над тепловыми потерями в широком интервале размеров неоднородностей. По расчетам этих авторов отношение тепловых потерь к вязким составляет приблизительно 2% для сердечной мышцы и значительно меньшую величину для кожи и крови. Мак-Куин [138] с позиций теории вязкого относительного движения попытался объяснить различные явления взаимодействия ультразвука с мягкими тканями, наблюдаемые в эксперименте. В частности, он рассмотрел эффект разрыва мелких кровеносных сосудов спинного мозга крысы при воздействии на мозг импульсным ультразвуком. В отличие от О'Доннелла и Миллера [166], которые использовали представление о суспензии «частиц», форма которых близка к сферической, Мак-Куин рассмотрел модель в виде системы волокон, пронизывающих вязкую среду. Возможно, что его представление является более реалистичным подходом при моделировании некоторых биологических тканей.
Другой механизм затухания ультразвука в суспензиях частиц рассмотрен в работе Кольцовой с соавт. [116]. Если частицы характеризуются высокой поверхностной активностью, то возможно образование ансамблей частиц с подвижной структурой, реакция которой на флуктуации звукового давления приводит к поглощению ультразвука по типу структурной релаксации. В случае суспензии частиц кварца в воде (диаметр частиц порядка 16 нм) этот вклад в поглощение приблизительно в 50 раз превышает суммарный вклад вязких, тепловых потерь и потерь на рассеяние в частотном диапазоне от 1 до 10 МГц. Неизвестно, однако, имеют ли место подобные процессы в биологических средах.
Поскольку процессы вязкого и теплового затухания включают в себя периодический обмен количеством движения и теплом между взвешенными частицами и средой и этот обмен происходит с конечной скоростью, то естественно, что такие процессы будут описываться уравнениями релаксационного типа. Так, Хьютер [104] учитывал эти механизмы при рассмотрении вязкоупругой модели биологической ткани. Вклад ![]() в коэффициент поглощения, обусловленный одиночным процессом вязкого относительного движения, определяется выражением [53]
в коэффициент поглощения, обусловленный одиночным процессом вязкого относительного движения, определяется выражением [53]
![]()
где ![]() ,
,
причем для сферических частиц
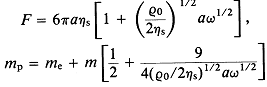
Здесь Vp — объемная концентрация взвешенных частиц, с — фазовая скорость звука на частоте ![]() и
и ![]() — плотности структурных элементов (частиц) и среды, mc — масса элемента. Уравнение (4.30) применимо в общем случае для структурных элементов произвольной формы. Сила трения F и эффективная масса элемента mр приведены для частного случая, когда отдельные элементы можно приблизительно рассматривать как частицы сферической формы. В этом случае
— плотности структурных элементов (частиц) и среды, mc — масса элемента. Уравнение (4.30) применимо в общем случае для структурных элементов произвольной формы. Сила трения F и эффективная масса элемента mр приведены для частного случая, когда отдельные элементы можно приблизительно рассматривать как частицы сферической формы. В этом случае ![]() , где
, где ![]() — радиус частицы, n — концентрация частиц и m — масса жидкости, вытесненной частицей. Между уравнением (4.30) и уравнением, описывающим частотную зависимость поглощения при обычном процессе релаксации, существует заметное различие. Оно заключается в том, что в случае вязкого относительного движения частота «релаксации» (
— радиус частицы, n — концентрация частиц и m — масса жидкости, вытесненной частицей. Между уравнением (4.30) и уравнением, описывающим частотную зависимость поглощения при обычном процессе релаксации, существует заметное различие. Оно заключается в том, что в случае вязкого относительного движения частота «релаксации» (![]() ) сама зависит от частоты. Как показано на рис. 4.1, г, это приводит к появлению пика поглощения, ширина которого значительно превосходит ширину пика, обусловленного одиночным процессом молекулярной релаксации.
) сама зависит от частоты. Как показано на рис. 4.1, г, это приводит к появлению пика поглощения, ширина которого значительно превосходит ширину пика, обусловленного одиночным процессом молекулярной релаксации.
Очевидно, что структура мягких биологических тканей весьма неоднородна. В них могут существовать локальные неоднородности самых различных размеров, форм и плотностей. Поэтому при анализе процессов молекулярной релаксации суммарный вклад в поглощение потерь, вызванных вязким относительным движением, можно было бы оценить на основе суммирования или интегрирования по некоторому интервалу размеров структурных частиц с учетом их формы и плотности. Для случая суспензии частиц, имеющих одинаковую плотность и ограниченный, узкий диапазон размеров, можно предсказать, что частотная зависимость аУ в области 1—10 МГц будет близка к линейной. Это, в частности, было показано в работе О'Доннелла и Миллера [166], в которой миофибрил-лы сердечной мышцы аппроксимировались частицами радиусом 1—2 мкм.
Если структурными неоднородностями являются газовые пузырьки, то относительный вклад теплового затухания может стать более существенным. Более заметным становится и рассеяние продольных волн (будем называть его в данном контексте «затуханием за счет излучения»). Это рассеяние вызвано большим различием акустических импедансов газа и жидкости, а также тем, что пузырьки могут иметь резонансные размеры. Хотя общему рассмотрению процессов рассеяния посвящена гл. 6, мы кратко рассмотрим их и здесь для полноты картины. При любом механизме затухания потеря акустической мощности на пузырьке газа будет максимальной, если частота ультразвуковой волны равна резонансной частоте пузырька. Эта резонансная частота определяется выражением [53]
![]()
![]() -отношение удельных теплоемкостеи газа в пузырьке,
-отношение удельных теплоемкостеи газа в пузырьке,
P -статическое давление,
Ts - поверхностное натяжение,
![]() -удельная теплоемкость газа при постоянном давлении,
-удельная теплоемкость газа при постоянном давлении,
![]() -удельная теплопроводность газа.
-удельная теплопроводность газа.
Если все газовые пузырьки в среде имеют одинаковые размеры, то их вклад (ag) в затухание определяется следующим образом:
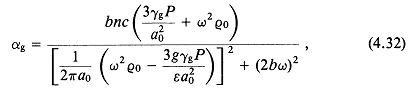
где b — так называемый параметр полных диссипативных потерь, представляющий собой сумму параметров тепловых потерь (bt), потерь на излучение (br) и вязких потерь (bv); n — концентрация пузырьков. Когда пузырьки имеют различные размеры, необходимо проводить суммирование или интегрирование по всем радиусам пузырьков. Параметры потерь на излучение и вязких потерь определяются соответственно выражениями
Приближенные выражения для параметра bt имеют вид
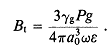
Обычно затухание ультразвука в твердых телах меньше, чем в жидкостях, причем механизмов такого затухания может быть очень много [144].
Так, некоторый вклад в затухание дает теплопроводность среды (см. выражение (4.12)), однако обычно такое затухание в твердых телах, за исключением металлов, мало. В твердых телах в килогерцевом диапазоне частот часто наблюдается явление, известное под названием термоупругой релаксации. Оно заключается в появлении тепловых потоков между локальными участками со случайными флуктуациями температуры. Различия в температуре возникают в соседних произвольно ориентированных кристаллических зернах в силу того, что соотношение между напряжением и деформацией в кристаллическом зерне зависит от его ориентации. Тепловое затухание может возникать также на дислокациях кристаллической решетки. Вклад этих эффектов в полное затухание звука также мал.
Затухание звука в твердых телах может быть обусловлено разнообразными резонансными потерями, которые зависят от частоты и могут иметь самую различную природу. Конкретный механизм таких потерь зависит от свойств рассматриваемого материала, его формы, а также его окружения. Примерами могут служить петли дислокаций в кристаллических решетках, магнитострикционный и пьезоэлектрический эффекты, взаимодействия с ядерными и электронными спиновыми системами при наличии внешнего магнитного поля.
Дислокации решетки могут быть также причиной нерезонансного поглощения звука релаксационного типа. Кроме того, они приводят к потерям на гистерезис, которые не зависят от частоты, но являются функцией амплитуды деформации.
Структурная релаксация в твердых телах проявляется в передаче энергии волны распределению квантованных колебательных состояний решетки (тепловых фононов). Она заметна в гигагерцевом диапазоне частот и велика в твердых телах при температурах, близких к точке плавления. Механизм затухания, обусловленный непосредственной передачей энергии волны заряженным носителям, играет важную роль в металлах в температурной области ниже 20 К. В полупроводниках величина такого затухания зависит от степени их легирования, а также от интенсивности внешнего светового потока. В последнем случае передача количеств движения от звуковой волны электронам проводимости приводит к возникновению дрейфового тока, который можно зарегистрировать по появлению постоянного электрического поля в образце. Этот эффект наряду с эффектом пьезоэлектричества используется при создании приемников ультразвука (гл. 3).
В поликристаллических твердых телах рассеяние волны на границах отдельных зерен приводит к недиссипативным потерям, которые могут быть основной причиной затухания ультразвука. На низких частотах, когда ![]() (d—средний диаметр зерен), затухание звука подчиняется закону Рэлея и пропорционально f4 и d3. По мере роста частоты в интервале
(d—средний диаметр зерен), затухание звука подчиняется закону Рэлея и пропорционально f4 и d3. По мере роста частоты в интервале ![]() коэффициент as становится пропорциональным f2 и d2. При дальнейшем повышении частоты
коэффициент as становится пропорциональным f2 и d2. При дальнейшем повышении частоты ![]() растет еще медленнее и стремится к некоторому не зависящему от f значению в области
растет еще медленнее и стремится к некоторому не зависящему от f значению в области ![]() , причем в этой области
, причем в этой области ![]() обратно пропорционален d.
обратно пропорционален d.
В случае металлов зависимость коэффициента поглощения от частоты в диапазоне порядка нескольких мегагерц подчиняется следующему закону:
![]()
Первый член в этом выражении характеризует потери, обусловленные пластическим гистерезисом, причем коэффициент А не зависит от размера зерен. Во втором члене, описывающем рассеяние, множитель В равен Rsd3/c3, где с — скорость звука и Rs — коэффициент упругой анизотропии (величина постоянная для данного материала и данного типа волны). Значения В, найденные в соответствии с выражением (4.37) путем интерполирования экспериментальных зависимостей ![]() от f, могут быть использованы для оценки размера зерен образцов различных металлов [147].
от f, могут быть использованы для оценки размера зерен образцов различных металлов [147].
Следует отметить, что некоторые биологические ткани можно рассматривать как твердый тела, к которым применимы полученные выше результаты. Известна по крайней мере одна работа [16], в которой исследуются свойства губчатой кости черепа человека и показано, что рассмотренная теория рассеяния обеспечивает приемлемое количественное описание этих свойств. В частности, проведенные измерения показали, что в частотном диапазоне от 0,3 до 1,3 МГц затухание ультразвука в таких костях пропорционально f4. При дальнейшем повышении частоты наблюдается постепенное насыщение затухания, причем в диапазоне от 1,3 до 1,8 МГц оно пропорционально f2.
4.3.5. ЗАВИСИМОСТЬ ЗАТУХАНИЯ ОТ ТЕМПЕРАТУРЫ
В средах небиологического происхождения характер зависимости затухания ультразвука от температуры может изменяться в очень широких пределах. Конкретный вид такой зависимости определяется частотой ультразвука, а также теми механизмами, которые ответственны за затухание. Можно предположить, что в случае биологических тканей картина еще более усложнится. Этого следует ожидать на том основании, что при анализе затухания необходимо учитывать множество различных механизмов, относительные вклады которых также могут зависеть от температуры и частоты.
Повышение температуры приводит к уменьшению времени релаксации ![]() согласно выражению
согласно выражению
![]()
где T—абсолютная температура среды, ![]() W—энергия активации данного процесса, R — универсальная газовая постоянная и то — некая константа. Уравнение (4.38) представляет собой модификацию хорошо известного уравнения Аррениуса для константы скорости в химической реакции первого порядка [152]. Следует отметить, что тепловым процессам свойственно только одно значение
W—энергия активации данного процесса, R — универсальная газовая постоянная и то — некая константа. Уравнение (4.38) представляет собой модификацию хорошо известного уравнения Аррениуса для константы скорости в химической реакции первого порядка [152]. Следует отметить, что тепловым процессам свойственно только одно значение ![]() W, однако величина энергии, необходимой для активации структурных превращений, зависит от локальных конфигураций молекул и поэтому постоянной величиной не является.
W, однако величина энергии, необходимой для активации структурных превращений, зависит от локальных конфигураций молекул и поэтому постоянной величиной не является.
Вводя величины ![]() , уравнение (4.38) можно преобразовать к виду
, уравнение (4.38) можно преобразовать к виду
![]()
Строя график зависимости ![]() от обратной величины абсолютной температуры (так называемый график Аррениуса), можно по полученным экспериментальным данным определить энергию активации в случае одиночного процесса релаксации. Для этого достаточно измерить угловой коэффициент наклона
от обратной величины абсолютной температуры (так называемый график Аррениуса), можно по полученным экспериментальным данным определить энергию активации в случае одиночного процесса релаксации. Для этого достаточно измерить угловой коэффициент наклона ![]() построенной прямой линии.
построенной прямой линии.
Анализ частотного смещения кривой ![]() , представленной на рис. 4.1, а, показывает, что температурный коэффициент поглощения должен быть отрицательным на частотах ниже значения fr и положительным на частотах, превышающих /R. .Кроме того, наблюдается изменение
, представленной на рис. 4.1, а, показывает, что температурный коэффициент поглощения должен быть отрицательным на частотах ниже значения fr и положительным на частотах, превышающих /R. .Кроме того, наблюдается изменение ![]() в зависимости от этого смещения. В характере температурной зависимости поглощения наблюдаются некоторые из наиболее интересных различий между тепловой и структурной релаксациями. В случае неассоциированных жидкостей, для которых свойственны процессы сравнительно низкочастотной химической релаксации наблюдаются следующие тенденции: величина
в зависимости от этого смещения. В характере температурной зависимости поглощения наблюдаются некоторые из наиболее интересных различий между тепловой и структурной релаксациями. В случае неассоциированных жидкостей, для которых свойственны процессы сравнительно низкочастотной химической релаксации наблюдаются следующие тенденции: величина ![]() положительна, отношение
положительна, отношение ![]() велико (от 101 до 103) и отсутствует какая-либо корреляция между температурными зависимостями величин
велико (от 101 до 103) и отсутствует какая-либо корреляция между температурными зависимостями величин ![]() и
и ![]() . В противоположность этому в ассоциированных жидкостях, для которых характерными являются процессы сравнительно высокочастотной структурной и сдвиговой релаксации, коэффициент
. В противоположность этому в ассоциированных жидкостях, для которых характерными являются процессы сравнительно высокочастотной структурной и сдвиговой релаксации, коэффициент ![]() отрицателен, а отношение
отрицателен, а отношение ![]() мало (от 1 до 3) и не зависит от температуры (обе величины
мало (от 1 до 3) и не зависит от температуры (обе величины ![]() и
и ![]() в этом случае отрицательны). В случае ассоциированных жидкостей между параметрами
в этом случае отрицательны). В случае ассоциированных жидкостей между параметрами ![]() и
и ![]() имеется корреляция. Она обусловлена тем, что воздействие как сдвиговых напряжений, так и напряжений сжатия приводит к изменению положения молекул жидкости в решетке. В обоих случаях нарушаются одни и те же связи, поэтому соответствующие значения энергии активации тесно взаимосвязаны. В некоторых жидкостях релаксационные процессы обоих рассмотренных типов действуют совместно, причем их относительный вклад зависит от температуры в пределах заданного частотного диапазона и интервала температур. В тех жидкостях, где сдвиговая вязкость играет основную роль (т. е. применима формула Стокса) или преобладает какой-либо процесс высокочастотной структурной релаксации (т. е. а пропорционален f2, как и в воде), зависимость коэффициента поглощения а от температуры представляет собой спадающую функцию, вид которой аналогичен температурной зависимости коэффициента сдвиговой вязкости, а именно
имеется корреляция. Она обусловлена тем, что воздействие как сдвиговых напряжений, так и напряжений сжатия приводит к изменению положения молекул жидкости в решетке. В обоих случаях нарушаются одни и те же связи, поэтому соответствующие значения энергии активации тесно взаимосвязаны. В некоторых жидкостях релаксационные процессы обоих рассмотренных типов действуют совместно, причем их относительный вклад зависит от температуры в пределах заданного частотного диапазона и интервала температур. В тех жидкостях, где сдвиговая вязкость играет основную роль (т. е. применима формула Стокса) или преобладает какой-либо процесс высокочастотной структурной релаксации (т. е. а пропорционален f2, как и в воде), зависимость коэффициента поглощения а от температуры представляет собой спадающую функцию, вид которой аналогичен температурной зависимости коэффициента сдвиговой вязкости, а именно ![]() , где В — константа и Е — энергия активации в случае стационарного потока.
, где В — константа и Е — энергия активации в случае стационарного потока.
Дисперсионная кривая скорости звука (рис. 4.1,6) также смещается по шкале частот при изменении температуры. В сочетании с уменьшением значений ![]() и
и ![]() такое смещение приводит к тому, что температурный коэффициент скорости
такое смещение приводит к тому, что температурный коэффициент скорости ![]() имеет отрицательные значения почти для всех жидкостей. Величина производной
имеет отрицательные значения почти для всех жидкостей. Величина производной ![]() по температуре в 2—4 раза превышает значения этой производной для плотности, тогда как соответствующий множитель для величины
по температуре в 2—4 раза превышает значения этой производной для плотности, тогда как соответствующий множитель для величины ![]() изменяется в интервале от 2 до 8. Своеобразное исключение представляют чистая вода, тяжелая вода и водные растворы. В этих средах скорость звука вначале возрастает до максимального значения при повышении температуры (в чистой воде максимум скорости достигается при 74 °С) и затем уменьшается (см. рис. 5.2). Растворение в воде каких-либо веществ приводит к изменению максимального значения скорости звука и к его смещению в сторону меньших температур. При малых концентрациях растворенных веществ температурная кривая скорости звука представляет собой параболу. Поэтому величина
изменяется в интервале от 2 до 8. Своеобразное исключение представляют чистая вода, тяжелая вода и водные растворы. В этих средах скорость звука вначале возрастает до максимального значения при повышении температуры (в чистой воде максимум скорости достигается при 74 °С) и затем уменьшается (см. рис. 5.2). Растворение в воде каких-либо веществ приводит к изменению максимального значения скорости звука и к его смещению в сторону меньших температур. При малых концентрациях растворенных веществ температурная кривая скорости звука представляет собой параболу. Поэтому величина ![]() характеризуется постоянной скоростью изменения и может быть экстраполирована к нулевому значению с целью нахождения температуры, при которой скорость звука максимальна. Такой экстраполяцией можно пользоваться в тех случаях, когда точка максимума лежит вне диапазона измерений. Наличие максимума скорости звука можно объяснить, если воспользоваться моделью двух состояний молекул в водных средах. В рамках этой модели предполагается, что среда состоит из структуры с рыхлой упаковкой (типа льда), находящейся в равновесии с другой структурой, имеющей более плотную упаковку. С ростом температуры результирующая сжимаемость такой среды (величина, обратная модулю всестороннего сжатия) возрастала бы как и в других жидкостях, если бы не тот факт, что с самого начала происходит смещение равновесия в сторону структуры с плотной упаковкой, сжимаемость которой меньше сжимаемости структуры типа льда. Действие двух этих конкурирующих процессов приводит к появлению минимума сжимаемости среды при определенной температуре, т. е. к образованию максимума скорости звука.
характеризуется постоянной скоростью изменения и может быть экстраполирована к нулевому значению с целью нахождения температуры, при которой скорость звука максимальна. Такой экстраполяцией можно пользоваться в тех случаях, когда точка максимума лежит вне диапазона измерений. Наличие максимума скорости звука можно объяснить, если воспользоваться моделью двух состояний молекул в водных средах. В рамках этой модели предполагается, что среда состоит из структуры с рыхлой упаковкой (типа льда), находящейся в равновесии с другой структурой, имеющей более плотную упаковку. С ростом температуры результирующая сжимаемость такой среды (величина, обратная модулю всестороннего сжатия) возрастала бы как и в других жидкостях, если бы не тот факт, что с самого начала происходит смещение равновесия в сторону структуры с плотной упаковкой, сжимаемость которой меньше сжимаемости структуры типа льда. Действие двух этих конкурирующих процессов приводит к появлению минимума сжимаемости среды при определенной температуре, т. е. к образованию максимума скорости звука.
Если имеет место некоторое распределение времен релаксации, то в рамках рассмотренной выше модели повышение температуры будет вызывать смещение всей кривой ![]() в сторону более высоких частот. В тех областях, где наклон этой кривой становится положительным, температурный коэффициент поглощения должен иметь небольшие отрицательные значения. С другой стороны, уменьшение
в сторону более высоких частот. В тех областях, где наклон этой кривой становится положительным, температурный коэффициент поглощения должен иметь небольшие отрицательные значения. С другой стороны, уменьшение ![]() с ростом частоты приводит к положительному температурному коэффициенту. Подобное рассмотрение является, конечно, предельно упрощенным, однако в дальнейшем будет показано, что оно обеспечивает по крайней мере качественную интерпретацию некоторых экспериментальных данных.
с ростом частоты приводит к положительному температурному коэффициенту. Подобное рассмотрение является, конечно, предельно упрощенным, однако в дальнейшем будет показано, что оно обеспечивает по крайней мере качественную интерпретацию некоторых экспериментальных данных.
Смещение частоты релаксации fR при изменении температуры часто с успехом используется в исследованиях вязкоупругих свойств материалов для получения данных в очень широком диапазоне частот, значительно превышающем диапазон реальных измерений. Для этой цели применяется метод приведенных переменных [62], основанный на возможности наложения ряда изотермических кривых, полученных для действительной и мнимой части комплексного модуля упругости, путем их смещения вдоль логарифмической оси частот. Было установлено, что такой метод наложения кривых применим даже в том случае, когда существует некоторое распределение времен релаксации, хотя при этом требуется, чтобы все времена релаксации имели приблизительно одинаковую температурную зависимость. Если бы последнее условие выполнялось в случае биологических тканей и если бы можно было пренебречь модулем сдвига (или считать, что времена сдвиговой и объемной релаксации характеризуются одинаковой температурной зависимостью), то рассмотренный метод в принципе можно было бы применить для получения данных о скорости и затухании звука в биологических тканях в широком диапазоне частот, превышающем диапазон измерений. Во всяком случае, попытки использования метода наложений позволяют оценить справедливость таких условий (см. разд. 4.5.2.5). Следует также отметить, что существенным препятствием на пути практической реализации метода приведенных переменных является ограниченность диапазона температур, в пределах которого биологические ткани можно подвергать ультразвуковому воздействию без риска их необратимых изменений.
Упомянутые выше температурные зависимости будут, еще более сложными, если неоднородности биологических тканей дают заметный вклад в затухание звука. Мы уже отмечали, что если преобладающим механизмом потерь является относительное движение взвешенных структурных частиц, то коэффициент затухания будет сильно зависеть от вязкости самой жидкости. О'Доннелл и др. [169], основываясь на разложении в ряд выражения типа (4.30), предположили, что коэффициент ![]() должен изменяться пропорционально изменению температуры, которое в свою очередь выражается как корень квадратный из изменения вязкости.
должен изменяться пропорционально изменению температуры, которое в свою очередь выражается как корень квадратный из изменения вязкости.
Нам не известны какие-либо работы, специально посвященные исследованию температурной зависимости компоненты затухания ![]() , обусловленной рассеянием продольной волны. Обычно предполагается, что в большинстве тканей
, обусловленной рассеянием продольной волны. Обычно предполагается, что в большинстве тканей ![]() представляет лишь малую часть
представляет лишь малую часть ![]() а (см. разд. 4.5.2.2). Исключением могут быть такие биологические ткани, в которых преобладающую роль играют неоднородности типа границ между участками жировой и нежировой ткани. По-видимому, к таким неоднородным тканям можно отнести молочную железу и костные структуры. Если пренебречь вариациями плотности, то
а (см. разд. 4.5.2.2). Исключением могут быть такие биологические ткани, в которых преобладающую роль играют неоднородности типа границ между участками жировой и нежировой ткани. По-видимому, к таким неоднородным тканям можно отнести молочную железу и костные структуры. Если пренебречь вариациями плотности, то ![]() становится пропорциональным квадрату флуктуаций сжимаемости (см. гл. 6), причем сжимаемость будет обратно пропорциональна квадрату скорости звука. Результаты измерений зависимости скорости звука от температуры в различных тканях (см. гл. 5) показывают, что температурный коэффициент
становится пропорциональным квадрату флуктуаций сжимаемости (см. гл. 6), причем сжимаемость будет обратно пропорциональна квадрату скорости звука. Результаты измерений зависимости скорости звука от температуры в различных тканях (см. гл. 5) показывают, что температурный коэффициент ![]() не должен иметь отрицательных значений в пределах температурного интервала, представляющего интерес для практики. Более того, для ряда тканей этот коэффициент должен принимать большие положительные значения.
не должен иметь отрицательных значений в пределах температурного интервала, представляющего интерес для практики. Более того, для ряда тканей этот коэффициент должен принимать большие положительные значения.
4.3.6. ВЛИЯНИЕ ВНЕШНЕГО ДАВЛЕНИЯ
Коэффициент поглощения и скорость звука зависят не только от температуры, но также и от давления окружающей среды. Хотя внешние давления, отличные от атмосферного, не принято использовать для исследования акустических свойств биологических тканей [53], такой подход применялся в случае жидкостей с целью выявления различий между возможными процессами релаксации. С учетом того, что температуру биологических тканей можно менять лишь в сравнительно малом интервале, представляется вполне целесообразным попытаться использовать различные внешние давления для получения подобных данных о тканях. Однако мы не располагаем сведениями, что кто-либо предпринимал подобные попытки.
Результаты экспериментов на жидкостях показали, что при повышении внешнего давления частота релаксации /r возрастает в случае колебательной релаксации, уменьшается в случае структурной релаксации и остается неизменной, если действующим механизмом является поворотная изомерия. В тех случаях, когда частота релаксации /r зависит от давления, ее относительное изменение составляет обычно от 20 до 50% от значения при нормальном атмосферном давлении при изменении давления на одну атмосферу. Следует отметить, что коэффициент поглощения обычно уменьшается, а скорость звука растет при повышении давления. Это затрудняет выявление различий между действующими релаксационными моделями, если только не наблюдается смещение области релаксации по частоте. За исключением воды, вязкость жидкостей обычно возрастает при повышении внешнего давления.
Отметим, что метод приведенных переменных, рассмотренный ранее применительно к вариациям температуры, может быть также использован и в случае изменения давления [180].
4.3.7. ВЗАИМОСВЯЗЬ ЯВЛЕНИЙ ПОГЛОЩЕНИЯ, ДИСПЕРСИИ, ЗАТУХАНИЯ И РАССЕЯНИЯ ЗВУКА
Исторически исследования механизмов распространения акустических волн развивались таким образом, что вопросы поглощения и рассеяния волн рассматривались, как правило, раздельно. Такое разграничение между физическими явлениями, возникающими в среде при прохождении волны, представляется в определенной степени искусственным и требует пересмотра. Как отмечали О'Доннелл и др. [167, 168], в теории, рассматривающей механизмы акустических потерь, существует еще много неясных моментов. Особенно это касается дисперсии скорости звука. Отсутствует четкое разграничение между различными механизмами потерь. В частности, локальное поглощение акустической энергии можно трактовать как некий предельный случай явления рассеяния. Более того, существует феноменологическая теория, в рамках которой дисперсия скорости звука возникает в среде только при наличии частотно-зависимого затухания, которое может быть обусловлено действием любого из ранее рассмотренных механизмов потерь. При этом волновое число определяется комплексной скоростью, т. е. ![]()
![]() , где
, где ![]() — фазовая скорость. При отсутствии поглощения рассеяние может приводить к дисперсии скорости звука. Так, например, Бергман [17] определял дисперсию скорости распространяющейся волны, задавая лишь переменный показатель преломления среды
— фазовая скорость. При отсутствии поглощения рассеяние может приводить к дисперсии скорости звука. Так, например, Бергман [17] определял дисперсию скорости распространяющейся волны, задавая лишь переменный показатель преломления среды
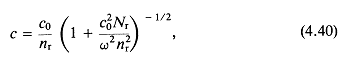
где с— фазовая скорость, nr — показатель преломления и Nr — параметр, определяющий элементарные источники рассеянных волн (см. правую часть уравнения (6.5)). Если в среде отсутствуют градиенты показателя преломления, то параметр Nr стремится к нулю и скорость распространения волны становится равной c0/nr. Однако в общем случае чем ниже частота, тем значительнее уменьшение скорости распространения из-за рассеяния. Используя феноменологические соотношения
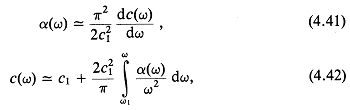
где ![]() представляет собой некоторую выбранную опорную частоту, a
представляет собой некоторую выбранную опорную частоту, a ![]() — фазовая скорость на этой частоте, О'Доннелл и др. [167, 168] показали, что в целом ряде сред зависимость скорости звука от частоты может быть однозначно выражена через измеренную частотную зависимость коэффициента затухания. Эти авторы пришли к выводу, что неправомерно использовать сопоставление затухания и дисперсии скорости как единственное доказательство того, что затухание обусловлено каким-либо определенным механизмом потерь. Уравнения (4.41) и (4.42) представляют собой приближенные соотношения, полученные из точных формул в предположении, что затухание и дисперсия достаточно малы и изменяются незначительно в пределах рассматриваемого частотного диапазона. Такое допущение, по-видимому, справедливо для многих биологических сред в диапазоне частот, характерном для медицинских приложений. В точном виде указанные уравнения по своей форме аналогичны дисперсионным соотношениям, выведенным в теории электромагнитных волн. Эти соотношения показывают, что действительная часть относительной диэлектрической проницаемости зависит от вариации ее мнимой части во всем диапазоне частот и наоборот [42]. Из уравнения (4.42) следует, что если затухание пропорционально квадрату частоты, то приращение скорости звука
— фазовая скорость на этой частоте, О'Доннелл и др. [167, 168] показали, что в целом ряде сред зависимость скорости звука от частоты может быть однозначно выражена через измеренную частотную зависимость коэффициента затухания. Эти авторы пришли к выводу, что неправомерно использовать сопоставление затухания и дисперсии скорости как единственное доказательство того, что затухание обусловлено каким-либо определенным механизмом потерь. Уравнения (4.41) и (4.42) представляют собой приближенные соотношения, полученные из точных формул в предположении, что затухание и дисперсия достаточно малы и изменяются незначительно в пределах рассматриваемого частотного диапазона. Такое допущение, по-видимому, справедливо для многих биологических сред в диапазоне частот, характерном для медицинских приложений. В точном виде указанные уравнения по своей форме аналогичны дисперсионным соотношениям, выведенным в теории электромагнитных волн. Эти соотношения показывают, что действительная часть относительной диэлектрической проницаемости зависит от вариации ее мнимой части во всем диапазоне частот и наоборот [42]. Из уравнения (4.42) следует, что если затухание пропорционально квадрату частоты, то приращение скорости звука ![]() будет линейно зависеть от частоты, как и в средах, характеризующихся только классическими вязкими потерями. Если же зависимость затухания от частоты линейна, то приращение
будет линейно зависеть от частоты, как и в средах, характеризующихся только классическими вязкими потерями. Если же зависимость затухания от частоты линейна, то приращение ![]() должно изменяться в зависимости от частоты по логарифмическому закону. Как показывают экспериментальные исследования, приблизительно логарифмическая зависимость наблюдается в биологических средах и мягких тканях.
должно изменяться в зависимости от частоты по логарифмическому закону. Как показывают экспериментальные исследования, приблизительно логарифмическая зависимость наблюдается в биологических средах и мягких тканях.
Еще один аспект нечеткого разграничения между явлениями рассеяния и поглощения касается механизмов потерь, рассмотренных ранее в разделе о поглощении в неоднородных средах. Потери, вызванные как вязким относительным движением, так и тепловым затуханием, можно рассматривать на основе явлений рассеяния. Морз и Ингард [154] при оценке сечений поглощения и рассеяния в случае нежесткой сферы рассмотрели эти эффекты, исходя из анализа распространения рассеянных тепловой и сдвиговой волн, которые быстро затухают в пограничном слое, непосредственно примыкающем к поверхности сферы. Предполагалось, что амплитуды этих волн сравнительно велики и что на поверхности рассеивающей сферы выполняются граничные условия для температуры и тангенциальной компоненты скорости. При этом форма продольной рассеянной волны мало отличается от формы, рассчитанной в пренебрежении вязкими и тепловыми потерями, однако сечение поглощения такой волны существенно зависит от этих потерь. Было показано, что вязкие потери в случае сдвиговой волны происходят на неоднородностях плотности среды, тогда как тепловое затухание обусловлено флуктуациями сжимаемости. Максимумы на кривых поглощения ![]() соответствовали частотам, при которых длины сдвиговых и тепловых волн приблизительно равнялись радиусу сферического рассеивателя.
соответствовали частотам, при которых длины сдвиговых и тепловых волн приблизительно равнялись радиусу сферического рассеивателя.
До сих пор анализ механизмов потерь проводился в предположении, что реакция исследуемой среды на механические напряжения, вызванные акустической волной, линейна. В действительности такое предположение справедливо только в тех случаях, когда амплитуда волны очень мала. В данном разделе мы рассмотрим условия, при которых распространение акустических волн в жидкостях и мягких биологических тканях должно быть заметно нелинейным. Будет рассмотрено также влияние нелинейного распространения волн на реальные значения затухания в среде.
Некоторые аспекты нелинейного распространения акустических волн рассмотрены в упоминавшихся ранее работах Фрая и Данна [75], а также Данна и др. [53]. Теоретические основы были кратко изложены в гл. 1 данной книги применительно к средам без затухания. К сожалению, одна из наиболее исчерпывающих работ по данной тематике, а именно работа Бейера [18], практически недоступна. Однако и более ранние работы [19, 20] не утратили своей ценности и до сих пор представляют большой интерес. Совсем недавно были опубликованы статьи целого ряда авторов, исследовавших нелинейные эффекты при условиях, характерных для медицинских применений ультразвука [33, 85, 127, 128, 158] (см. также разд. 2.7 настоящей книги).
В разд. 1.8 было показано, что в общем случае нелинейного распространения решение волнового уравнения можно получить на основе его разложения в ряд по малым параметрам, характеризующим свойства среды. Учет только двух первых членов разложения в ряд Тейлора приводит к линейной теории или теории первого порядка. Нелинейная теория или теория второго порядка базируется на учете квадратичного члена разложения. При этом без учета потерь взаимосвязь между акустическим давлением и флуктуациями плотности среды описывается уравнением (1.195)
где обозначения те же, что и в гл. 1.
Из квадратичной зависимости акустического давления от плотности среды непосредственно следует, что волна будет распространяться с фазовой скоростью, зависящей от локальных значений колебательной скорости или давления
![]()
где ![]() _ колебательная скорость частиц, с0 — скорость звука в линейном приближении,
_ колебательная скорость частиц, с0 — скорость звука в линейном приближении, ![]() и отношение В/А называется нелинейным параметром среды. Это означает, что области сжатия, или гребни, волны распространяются с несколько большей, а области разряжения, или впадины, — с несколько меньшей скоростью по сравнению со скоростью с0, предсказываемой линейной теорией. В результате по мере распространения накапливается искажение профиля волны, который становится постепенно все круче, и волна первоначально синусоидальной формы преобразуется в пилообразную волну, если только затухание не нарушает этой картины (рис. 4.3, а—в). Соответствующее изменение формы волны, которая первоначально имела вид
и отношение В/А называется нелинейным параметром среды. Это означает, что области сжатия, или гребни, волны распространяются с несколько большей, а области разряжения, или впадины, — с несколько меньшей скоростью по сравнению со скоростью с0, предсказываемой линейной теорией. В результате по мере распространения накапливается искажение профиля волны, который становится постепенно все круче, и волна первоначально синусоидальной формы преобразуется в пилообразную волну, если только затухание не нарушает этой картины (рис. 4.3, а—в). Соответствующее изменение формы волны, которая первоначально имела вид ![]() , описывается следующим решением волнового уравнения второго порядка, полученным Фубини (см. [20]):
, описывается следующим решением волнового уравнения второго порядка, полученным Фубини (см. [20]):
![]()
Это выражение можно разложить в ряд Фурье
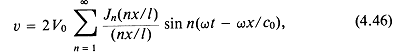
где ![]() —константа, зависящая от нелинейных свойств среды. Хотя данное решение справедливо только для значений х <
—константа, зависящая от нелинейных свойств среды. Хотя данное решение справедливо только для значений х < ![]() , из уравнения (4.46) непосредственно следует, что по мере распространения волны происходит уменьшение амплитуды основной гармоники, энергия которой передается в высшие гармоники.
, из уравнения (4.46) непосредственно следует, что по мере распространения волны происходит уменьшение амплитуды основной гармоники, энергия которой передается в высшие гармоники.
Расстояние от излучателя до точки х = I называется расстоянием до разрыва и определяется как
![]()
Это расстояние, на котором в отсутствие затухания производная ![]() становится отрицательно бесконечной, т. е. в волне появляется разрыв, представляющий собой ударный фронт. При х =
становится отрицательно бесконечной, т. е. в волне появляется разрыв, представляющий собой ударный фронт. При х = ![]() волна приобретает все более пилообразную форму и ударный фронт нарастает. Хотя представленный анализ справедлив при отсутствии в среде диссипативных потерь, он позволяет получить ряд основных закономерностей нелинейного распространения.
волна приобретает все более пилообразную форму и ударный фронт нарастает. Хотя представленный анализ справедлив при отсутствии в среде диссипативных потерь, он позволяет получить ряд основных закономерностей нелинейного распространения.
Во-первых, чем больше нелинейный параметр В/А, тем раньше происходит формирование ударного фронта и тем больше искажается профиль волны на заданном расстоянии от излучателя. Отметим, что в линейном приближении параметр В/А обращается в нуль. Экспериментальные методы определения нелинейного параметра В/А основаны либо на измерении зависимости скорости звука от температуры и давления [128, 140], либо на регистрации спектрального состава волны [128]. Значения В/А для газов лежат в интервале от 0 до 1, для жидкостей и твердых тел этот параметр может изменяться от 2 до 13. Нелинейный параметр слабо растет при повышении температуры или давления. В табл. 4.1 представлены значения В/А для ряда веществ, в том числе и для некоторых биологических тканей.
Таблица 4.1 Значение нелинейного параметра В/Л ряда жидкостей и биологических тканей при атмосферном давлении и температуре 20 ° С
Рис. 4.3. Эволюция синусоидальной волны по мере распространения в нелинейной среде с малым затуханием и дисперсией. Волна возбуждается в точке х = 0 в момент времени t = 0. а — Генерация исходной синусоидальной волны на излучателе; б — образование ударного фронта в результате накопления нелинейных искажений; в — нарастание ударного фронта (образование пилообразной волны); r — обеднение спектра волны высокочастотными гармониками (область стабилизации); д — затухание и возврат к синусоидальной форме волны на больших расстояниях от излучателя
|
Среда |
В/А |
Ссылка |
|
Дистиллированная вода |
5,0 |
Бейер [18] |
|
Морская вода (3,5%) |
5,25 |
То же |
|
Метиловый спирт |
9,6 |
‘’ |
|
Этиловый спирт |
10,5 |
‘’ |
|
Ацетон |
9,2 |
‘’ |
|
Этиленгликоль (30 °С) |
9,7 |
‘’ |
|
Четыреххлористый углерод (30 °С) |
11,54 |
Бьёрно [23] |
|
Глицерин |
8,8 |
То же |
|
Фреон |
12,41 |
Мадгоски и др. [140] |
|
Силиконовый каучук марки RTV 602 (0 °С) |
13,4 |
То же |
|
Макромолекулы в растворе (30 °С) |
0,053—0,0761} |
Лоу и др. [127] |
|
Цельная кровь |
6,3 |
То же |
|
Гомогенизированная печень |
|
Данн и др. [54] |
|
(23 и 30 °С) |
6,8 |
Лоу и др. [128] |
|
Цельная печень (23 и 30 ° С) |
7,8 |
Данн и др. [54] |
|
|
|
Лоу и др. [128] |
|
Свиной жир (30 °С) |
11,1 |
То же |
1) В качестве растворенных веществ использовались декстроза, сахароза, декстран, бычий сывороточный альбумин и гемоглобин. Указанные значения относятся к величине (B/Apacтвор — B/Aвода) деленной на концентрацию раствора в г/100 см3. Наблюдалась приблизительно линейная зависимость от концентрации.
Предварительные исследования, выполненные Лоу и др. [127, 128], показывают, что нелинейный параметр линейно зависит от концентрации макромолекул и не зависит от молекулярного веса. Эти результаты позволяют предположить, что межмолекулярные и внутримолекулярные взаимодействия в растворенных веществах практически не влияют на величину В/А. Наиболее вероятным источником нелинейности следует считать взаимодействия между молекулами растворенного вещества и растворителя. Из данных, приведенных для цельной и гомогенизированной печени, видно также, что на значение В/А оказывает влияние макроструктура ткани.
Во-вторых, нелинейные эффекты развиваются скорее на высоких частотах по сравнению с низкими. Это обусловлено накапливающимся характером этих эффектов по мере распространения волны, и при фиксированном расстоянии нелинейные эффекты будут проявляться тем сильнее, чем большее число длин волн укладывается в пределах данного расстояния.
В-третьих, чем больше начальная амплитуда волны, тем короче расстояние до разрыва. И наоборот, если V0 стремится к нулю, то ![]() стремится к бесконечности, что соответствует переходу к линейной теории.
стремится к бесконечности, что соответствует переходу к линейной теории.
И наконец, чем меньше скорость звука в среде, тем короче становится расстояние до разрыва ![]() и тем большее искажение профиля волны наблюдается на фиксированном расстоянии от излучателя. Бейер [18], а также Мадгоски и др. [140] показали, что в однородных средах небиологического происхождения параметр В/А в первом приближении линейно зависит от обратной величины скорости звука. В общем случае наблюдаемое нелинейное искажение может изменяться в различных средах в более широких пределах, чем это следовало бы исключительно из различий в значении нелинейного параметра В/А. Следует отметить, что, по данным Лоу и др. [127] величина В/А растет с ростом скорости звука в воде (в интервале температур 0—60 °С) и в водных растворах биологических макромолекул. В тех биологических средах, которые были исследованы до настоящего времени, скорость звука не слишком заметно влияла на наблюдаемые нелинейные искажения акустических волн.
и тем большее искажение профиля волны наблюдается на фиксированном расстоянии от излучателя. Бейер [18], а также Мадгоски и др. [140] показали, что в однородных средах небиологического происхождения параметр В/А в первом приближении линейно зависит от обратной величины скорости звука. В общем случае наблюдаемое нелинейное искажение может изменяться в различных средах в более широких пределах, чем это следовало бы исключительно из различий в значении нелинейного параметра В/А. Следует отметить, что, по данным Лоу и др. [127] величина В/А растет с ростом скорости звука в воде (в интервале температур 0—60 °С) и в водных растворах биологических макромолекул. В тех биологических средах, которые были исследованы до настоящего времени, скорость звука не слишком заметно влияла на наблюдаемые нелинейные искажения акустических волн.
Разумная оценка наиболее вероятной пиковой интенсивности акустических импульсов на выходе диагностической эхо-импульсной аппаратуры медицинского назначеия составляет примерно 20 Вт/см2. В водоподобных средах это соответствует начальной амплитуде колебательной скорости Ко, приблизительно равной 0,5 м/с, или амплитуде звукового давления около 8 атм. В табл. 4.2 для ряда сред приведены расчетные значения расстояния до разрыва ![]() , соответствующие указанной величине амплитуды колебательной скорости. По этим значениям можно судить, насколько быстро могут накапливаться нелинейные искажения при отсутствии затухания звука.
, соответствующие указанной величине амплитуды колебательной скорости. По этим значениям можно судить, насколько быстро могут накапливаться нелинейные искажения при отсутствии затухания звука.
Таблица 4.2 Значения параметров, связанных с нелинейным распространением ультразвука в ряде сред, при интенсивности на излучателе, соответствующей пиковой интенсивности стандартной диагностической аппаратуры
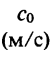
| 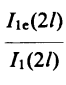
| ||||||||||
Как видно из рис. 4.3, г и д, наличие в среде зависящего от частоты затухания приводит к постепенному уменьшению амплитуды волны и обеднению ее гармониками, причем гармоники высших порядков исчезают первыми. В результате на некотором расстоянии от излучателя в волне останется лишь составляющая основной частоты и дальнейшее распространение волны подчиняется линейной теории. Для каждой гармонической составляющей существует определенный интервал расстояний (называемый областью стабилизации), в пределах которого скорость передачи энергии в данную гармонику приблизительно равна скорости уменьшения ее энергии за счет затухания. Именно в этой области каждая гармоника достигает максимума и затем начинает спадать по амплитуде. Некоторые авторы пытались применить различные приближенные методы с целью введения затухания в выражения, описывающие зависимость амплитуд основной гармоники и гармонических составляющих высших порядков от расстояния [18, 20]. Анализ проводился только для непрерывных волн. В этом плане следует отметить работу Фрая и Данна [75], которые учитывали только передачу энергии из основной частоты во вторую гармонику и пренебрегали всеми остальными процессами обмена энергией между различными гармониками. Строго говоря, их анализ применим только для области ![]() , однако полученное ими выражение для интенсивности основной гармоники действительно дает интенсивность
, однако полученное ими выражение для интенсивности основной гармоники действительно дает интенсивность ![]() 0 при х = 0, а при
0 при х = 0, а при ![]() стремится к величине
стремится к величине ![]() .
.
Из этого выражения можно оценить отношение ![]() (интенсивности основной гармоники в приближении линейной теории) к
(интенсивности основной гармоники в приближении линейной теории) к ![]() , а именно
, а именно
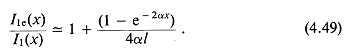
В табл. 4.2 приведены некоторые расчетные величины, полученные в соответствии с выражениями (4.48) и (4.49). Последний столбец таблицы характеризует относительное увеличение (в процентах) среднего значения коэффициента затухания звука за счет нелинейных эффектов при прохождении волны от излучателя до точки 21 в предположении, что наблюдается только основная частота. Эти значения рассчитаны по формуле
где ![]() — коэффициент затухания при нелинейном распространении. Представленные данные показывают, что при определенных условиях наличие нелинейных эффектов может привести к существенным погрешностям при измерениях затухания и поглощения [21, 85].
— коэффициент затухания при нелинейном распространении. Представленные данные показывают, что при определенных условиях наличие нелинейных эффектов может привести к существенным погрешностям при измерениях затухания и поглощения [21, 85].
Очевидно, что погрешности измерения затухания звука, связанные с нелинейным характером распространения волны, зависят от множества параметров, включая не только уже рассмотренные ранее величины ![]() , но также и расстояние от излучателя до той области, где проводятся измерения. В общем случае можно утверждать, что неэкспоненциальный характер затухания волн конечной амплитуды приводит к пространственному изменению коэффициента затухания. В частности, на расстояниях, очень близких и очень далеких от излучателя, он приблизительно равен коэффициенту затухания для волн бесконечно малой амплитуды, а в области стабилизации волны его значение достигает максимума. Ситуация осложняется еще тем, что на практике для подобных измерений применяются самые разнообразные методы (см. разд. 4.4). Используются как непрерывный, так и импульсный режимы излучения, при этом регистрируется либо пиковая амплитуда сигнала, либо спектральное распределение энергии. Одни приемники акустических волн могут регистрировать энергию сигнала и поэтому воспринимать все гармонические составляющие спектра непрерывного излучения источника. Другие могут обладать резонансными свойствами и быть чувствительными только к гармоникам нечетных порядков. Кроме того, одни приемники могут регистрировать сигналы в широкой, хотя и ограниченной, полосе частот, другие же являются узкополосными и воспринимают только сигнал основной частоты. В каждом конкретном случае методы теоретического анализа будут различными. Некоторые из них уже рассматривались [20], однако следует подчеркнуть, что наиболее общими и перспективными представляются компьютерные методы численного анализа [95]. Напомним, что пример нелинейного распространения акустических волн уже был рассмотрен в разд. 2.7.
, но также и расстояние от излучателя до той области, где проводятся измерения. В общем случае можно утверждать, что неэкспоненциальный характер затухания волн конечной амплитуды приводит к пространственному изменению коэффициента затухания. В частности, на расстояниях, очень близких и очень далеких от излучателя, он приблизительно равен коэффициенту затухания для волн бесконечно малой амплитуды, а в области стабилизации волны его значение достигает максимума. Ситуация осложняется еще тем, что на практике для подобных измерений применяются самые разнообразные методы (см. разд. 4.4). Используются как непрерывный, так и импульсный режимы излучения, при этом регистрируется либо пиковая амплитуда сигнала, либо спектральное распределение энергии. Одни приемники акустических волн могут регистрировать энергию сигнала и поэтому воспринимать все гармонические составляющие спектра непрерывного излучения источника. Другие могут обладать резонансными свойствами и быть чувствительными только к гармоникам нечетных порядков. Кроме того, одни приемники могут регистрировать сигналы в широкой, хотя и ограниченной, полосе частот, другие же являются узкополосными и воспринимают только сигнал основной частоты. В каждом конкретном случае методы теоретического анализа будут различными. Некоторые из них уже рассматривались [20], однако следует подчеркнуть, что наиболее общими и перспективными представляются компьютерные методы численного анализа [95]. Напомним, что пример нелинейного распространения акустических волн уже был рассмотрен в разд. 2.7.
Под действием звуковой волны находящиеся в среде газовые пузырьки субмикроскопических размеров начинают расти. Механизм их роста связан с процессом, известным под названием выпрямленной диффузии. Суть его состоит в следующем. В фазе разрежения при пониженном давлении газ диффундирует из раствора внутрь пузырька. В фазе повышенного давления диффузия газа происходит из пузырька в раствор. Однако в фазе разрежения площадь поверхности пузырька больше, поэтому в этой фазе внутрь пузырька поступает большее количество газа, чем выходит из него в течение полупериода сжатия. Поэтому на протяжении некоторого числа периодов колебаний размеры пузырьков будут возрастать. В конечном счете пузырьки достигнут резонансных размеров, соответствующих данной частоте ультразвука. Эти размеры определяются формулой (4.31) из разд. 4.3.3; например, резонансный диаметр пузырьков составляет примерно 6 мкм на частоте 1 МГц. При резонансе амплитуда колебаний пузырьков может на несколько порядков превысить амплитуду смещения в падающей волне. Рассмотренный процесс называется «стабильной» кавитацией и приводит к дегазации жидкости, содержащей растворенный газ. Стабильная кавитация существенно отличается от кавитации другого типа, известной как нестационарная или коллапсирующая кавитация. Такой процесс возникает в среде только при очень высоких интенсивностях ультразвука (пороговое значение интенсивности на частоте 1 МГц составляет примерно 300 Вт/см2). Возникновение кавитации приводит к изменению физических свойств среды и она может быть причиной неправильного измерения затухания и скорости звука. Поэтому при проведении подобных измерений необходимо выбрать такую методику и такой режим ультразвукового воздействия, которые гарантировали бы отсутствие кавитации. Следует отметить, что пороги возникновения кавитации зависят от амплитуды колебательного давления в звуковой волне, частоты, температуры, внешнего давления, длительности ультразвукового импульса, вязкости среды, а также от концентрации растворенного газа. Более полное и детальное рассмотрение кавитационных явлений проводится в гл. 12.
4.4. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТОВ ЗАТУХАНИЯ И ПОГЛОЩЕНИЯ В БИОЛОГИЧЕСКИХ ТКАНЯХ
В рамках данной книги не представляется возможным провести всесторонний анализ огромного числа существующих методов измерения затухания ультразвука в различных средах. Однако следует отметить, что из всего этого разнообразия лишь сравнительно небольшое число методов пригодно для измерения затухания в биологических тканях на частотах, характерных для медицинских приложений. Методам измерений в твердых телах, жидкостях и газах посвящены обзорные работы ряда авторов, в том числе Бейера и Летчера [20], Губермана [82], Матесона [145], а также Мак-Скимина [139]. Данн и др. [53] приводят в своей работе обширную библиографию статей, знакомящих читателя с классификацией и описанием методов измерения затухания продольных и сдвиговых акустических волн, а также скорости звука на различных частотах. Весьма полезной представляется статья Госса и др. [89], авторы которой на основе собственных экспериментов проводят сравнительный анализ различных методов измерений.
Приблизительно с 1973 г. наметился ряд новых подходов к измерению затухания. В первую очередь среди них следует отметить методы, обеспечивающие возможность измерений затухания как непрерывной функции частоты, методы регистрации пространственных изменений коэффициента затухания, а также методы, предназначенные для измерений in vivo. Указанные возможности представляют большой интерес для медицинских приложений ультразвука, поэтому в дальнейшем мы еще остановимся на этих нетрадиционных методах.
Проведение тщательного анализа погрешностей каждого из существующих методов измерений не представляется возможным. Связано это прежде всего с тем, что, к сожалению, авторы многих публикаций, видимо, не проводили необходимой работы по определению и анализу ошибок измерения. Некоторые характерные причины возникновения погрешностей при измерениях затухания ультразвука рассматриваются в разд. 4.4.2. Их необходимо учитывать при обсуждении сравнительных достоинств различных методов измерений. Следует также отметить, что многие из устройств, предназначенных для измерения затухания звука, можно использовать и для измерений скорости звука. Поэтому мы вновь вернемся к подобным устройствам в гл. 5.
4.4.1.1. Поглощение звука в биологических тканях
На рис. 4.4 представлена схематическая классификация различных методов измерения ультразвуковых потерь. В рамках данной классификации прежде всего следует провести различие между методами, обеспечивающими измерение коэффициента затухания, и методами, позволяющими непосредственно измерить коэффициент поглощения.
Рис. 4.4. Классификация способов измерения акустических потерь (пояснения в тексте). Данная классификация носит отчасти искусственный характер, поскольку многие методы взаимосвязаны друг с другом.
Естественно, что такое разделение имеет смысл в случае неоднородных сред, поскольку для однородных материалов результаты точного измерения затухания дают, по сути дела, численные значения коэффициента поглощения. Очень мало работ посвящено непосредственным измерениям коэффициента поглощения аа в биологических тканях (в противоположность косвенным оценкам поглощения по результатам измерений затухания и рассеяния звука). Следует также отметить, что во многих ранних работах не проводится четкое различие между понятиями поглощения и затухания. К счастью, в настоящее время это положение меняется, однако иногда еще требуется осторожно подходить к опубликованным данным во избежание недоразумений.
Метод нестационарного нагрева, разработанный Фраем и Фраем [76, 77], Фраем и Данном [75], Данном и др. [53], а также Госсом и др. [89] и основанный на регистрации скорости повышения температуры в локальной области (с помощью термопарного датчика), является примером тех методов, в которых измеряется именно та часть ультразвуковой энергии, которая поглощается средой и необратимо переходит в тепло. Суть его состоит в следующем. Датчик в виде термопарного спая, размеры которого малы по сравнению с длиной волны, вводят в исследуемый образец, после чего образец подвергают воздействию коротких импульсов плоских ультразвуковых волн заданной частоты. На протяжении нескольких десятых долей секунды от начала воздействия наблюдается быстрое повышение температуры датчика, обусловленное поглощением энергии за счет вязкого относительного движения среды и проволочек, образующих термопару. Этот участок температурной кривой становится более выраженным на низких частотах или при малом поглощении в среде, что ограничивает применимость данного метода в низкочастотной области (наименьшая частота составляет примерно 300 кГц). Дальнейшее повышение температуры в течение примерно одной секунды носит сравнительно линейный характер и обусловлено локальным поглощением звука в образце. Коэффициент поглощения образца определяется по начальному наклону этого линейного участка температурной кривой, если известны такие параметры, как плотность среды, ее удельная теплоемкость при постоянном давлении, а также интенсивность акустического поля. Для оценки реального ![]() применяется итерационный метод, согласно которому первая расчетная оценка этого коэффициента, полученная на основе измерения интенсивности падающего поля, используется в качестве коэффициента затухания для определения реального значения интенсивности
применяется итерационный метод, согласно которому первая расчетная оценка этого коэффициента, полученная на основе измерения интенсивности падающего поля, используется в качестве коэффициента затухания для определения реального значения интенсивности ![]() в точке измерения при известном расстоянии от излучателя до термопарного датчика. Аналогичным образом проводятся последующие более точные оценки
в точке измерения при известном расстоянии от излучателя до термопарного датчика. Аналогичным образом проводятся последующие более точные оценки ![]() и
и ![]() . При этом сходимость полученного ряда значений аа нарушается, если полное затухание в среде слишком велико. В результате возможности данного метода становятся ограниченными и на высоких частотах. Этому способствуют также трудности создания широких плоских звуковых пучков и изготовления миниатюрных термопар. В частности, в биологических тканях с помощью термопарного метода можно проводить измерения на частотах, не превышающих 7 МГц. Результирующая погрешность измерения величины
. При этом сходимость полученного ряда значений аа нарушается, если полное затухание в среде слишком велико. В результате возможности данного метода становятся ограниченными и на высоких частотах. Этому способствуют также трудности создания широких плоских звуковых пучков и изготовления миниатюрных термопар. В частности, в биологических тканях с помощью термопарного метода можно проводить измерения на частотах, не превышающих 7 МГц. Результирующая погрешность измерения величины ![]() составляет по оценкам примерно 10—15%.
составляет по оценкам примерно 10—15%.
Помимо возможности прямого измерения коэффициента поглощения данный метод обладает еще теми достоинствами, что измерения могут проводиться по месту (in situ), в тканях живого организма (in vivo), а также в структурах малого размера (так, например, Данн [44] с помощью термопарного метода измерил коэффициент поглощения в спинном мозге мыши). Присутствие газовых пузырьков в образцах биологических тканей является серьезной проблемой при измерении затухания звука, однако такие пузырьки почти не влияют на результаты термоэлектрических измерений коэффициента поглощения [72].
Если величина ![]() очень мала, то для получения заметного приращения температуры приходится использовать ультразвук высокой интенсивности. При этом необходимо позаботиться о том, чтобы исключить возможность возникновения нелинейных эффектов, искажающих результаты измерений (см. разд. 4.3.8). Следует отметить, что термопарные датчики обладают большой инерционностью, поэтому с их помощью невозможно одновременно измерить скорость звука.
очень мала, то для получения заметного приращения температуры приходится использовать ультразвук высокой интенсивности. При этом необходимо позаботиться о том, чтобы исключить возможность возникновения нелинейных эффектов, искажающих результаты измерений (см. разд. 4.3.8). Следует отметить, что термопарные датчики обладают большой инерционностью, поэтому с их помощью невозможно одновременно измерить скорость звука.
Дальнейшее развитие этого метода привело к созданию автоматизированной системы измерений [40] и позволило провести более полный анализ возникающих погрешностей [86].
Недавно Паркер [175], основываясь на применении термопар, предложил новый метод, являющийся альтернативой методу нестационарного нагрева. Он назвал его методом затухания теплового импульса. Вместо ультразвукового импульса большой длительности, Паркер использовал короткий импульс ультразвука длительностью менее 0,1 с. Как и в предыдущем случае, вязкий нагрев в окрестности термопарного спая и нагревание за счет истинного поглощения в ткани происходят одновременно. После прекращения действия ультразвукового импульса тепло будет отводиться из области нагрева за счет теплопроводности среды. При этом на начальном участке температурной кривой, построенной по показаниям термопарного датчика, наблюдается быстрый спад температуры. Он связан с тем, что вязкий нагрев происходит только в малом объеме, непосредственно окружающем термопару. Затем в течение приблизительно 2 с кривая остывания начинает соответствовать реальному уменьшению температуры в окружающей ткани. Аппроксимируя этот участок кривой остывания на начальные моменты времени, Паркер определял полную поглощенную энергию и соответственно коэффициент поглощения. Было показано, что полученные таким способом результаты очень хорошо согласуются с данными измерений, выполненных с помощью метода нестационарного нагрева.
4.4.1.2. Затухание в биологических тканях
Анализ методов и реализующих их устройств для измерения затухания звука целесообразно проводить, разделяя их на узкополосные и широкополосные.
А. Узкополосные системы. Во многих случаях измерения затухания звука проводились с помощью устройств, которые можно классифицировать как узкополосные системы в том смысле, что излучаемый акустический сигнал содержит достаточно большое число периодов высокочастотных колебаний. При этом можно считать, что измерения выполняются практически на одной частоте. К этому классу относятся самые различные устройства, принципы работы которых рассмотрены в уже упоминавшейся в начале данного раздела литературе. Вообще говоря, такие устройства не обеспечивают возможности измерений затухания как непрерывной функции частоты. Однако ниже будет показано, что в некоторых приложениях импульсных методов [22, 187] излучаемые акустические сигналы фактически обладали достаточно широким частотным спектром. Это приводило к тому, что частоты, на которых проводились измерения, не были точно заданными. Кроме того, не учитывались изменения формы импульса вследствие дисперсии затухания [186] или эффекта компенсации фазы (см. разд. 4.4.2.3), что могло приводить к существенным погрешностям измерений.
Основной класс измерительных систем подобного типа образуют импульсные устройства, которые делятся на устройства с «фиксированным расстоянием» и устройства с «переменным расстоянием» [53, 139]. Под «расстоянием» здесь понимается расстояние между излучателем и приемником, которое может совпадать, а может и отличаться от пути прохождения звуковой волны через исследуемый образец. После излучения короткие импульсы ультразвука проходят через образец и регистрируются либо приемным преобразователем, ориентированным соосно с излучателем, либо самим излучающим преобразователем после отражения импульса от плоской границы раздела и его повторного прохождения через образец. Иногда последний метод называют эхо-импульсным, однако его не следует путать с эхо-импульсными методами измерения затухания in vivo, о которых пойдет речь в дальнейшем. К преимуществам импульсных методов следует отнести исключение возможности образования стоячих волн и нагрева образца за счет поглощения ультразвука.
В устройствах с переменным расстоянием [5, 73, 111, 178, 181] коэффициент а определяется по скорости изменения логарифма амплитуды принятого сигнала в зависимости от местоположения приемника или отражателя. При этом полученные результаты не зависят от значений коэффициентов отражения или эффективности электромеханического преобразования. Такие устройства позволяют определять абсолютные значения а, но при их использовании требуется учитывать дифракционные потери. Эти потери приводят к погрешностям измерения, которые пропорционально растут при снижении частоты. Кроме того, требуется, чтобы образец имел сравнительно большой объем (![]() 0,5 л). Устройства с переменным расстоянием обычно используются для измерений затухания на частотах выше 3 МГц, что позволяет проводить измерения с погрешностью не хуже ±5%. Если рабочий диапазон частот составляет 12—15 МГц, то измерения могут быть выполнены в образцах объемом всего в несколько миллилитров, при этом погрешности за счет дифракционных потерь незначительны [59]. В этом случае основные источники погрешностей связаны с калибровкой электронного блока обработки сигналов, с измерением расстояний, а также с взаимной юстировкой излучателя и приемника. При надлежащем контроле за температурой точность измерений в сравнительно однородных образцах может быть доведена до значений приблизительно ±0,5%. Устройства с переменным расстоянием обычно не используют для измерений в биологических тканях из-за трудностей изменения расстояния между излучателем и приемником в нежидких средах. Как правило, эти устройства применяются для исследования биологических растворов и жидкостей на частотах вплоть до 200 МГц [83, 96, 126, 188].
0,5 л). Устройства с переменным расстоянием обычно используются для измерений затухания на частотах выше 3 МГц, что позволяет проводить измерения с погрешностью не хуже ±5%. Если рабочий диапазон частот составляет 12—15 МГц, то измерения могут быть выполнены в образцах объемом всего в несколько миллилитров, при этом погрешности за счет дифракционных потерь незначительны [59]. В этом случае основные источники погрешностей связаны с калибровкой электронного блока обработки сигналов, с измерением расстояний, а также с взаимной юстировкой излучателя и приемника. При надлежащем контроле за температурой точность измерений в сравнительно однородных образцах может быть доведена до значений приблизительно ±0,5%. Устройства с переменным расстоянием обычно не используют для измерений в биологических тканях из-за трудностей изменения расстояния между излучателем и приемником в нежидких средах. Как правило, эти устройства применяются для исследования биологических растворов и жидкостей на частотах вплоть до 200 МГц [83, 96, 126, 188].
В импульсных устройствах с фиксированным расстоянием принцип измерений основан на использовании либо метода замещения, предложенного Шваном и Карстенсеном [189], либо метода введения образца, разработанного Эше [57] (см. также работу Кремкау и др. [118]). Эти устройства характеризуются малыми величинами дифракционных поправок и менее жесткими требованиями к юстировке преобразователей. Однако они позволяют определять лишь относительные значения коэффициента затухания на основе сравнения с измерениями в эталонной жидкости, которой обычно является вода. В методе Швана и Карстенсена, с помощью которого они исследовали свойства крови в частотном диапазоне 0,3—20 МГц [31], излучающий и приемный преобразователи жестко связаны между собой и перемещаются в пространстве синхронно. При этом излучатель движется в эталонной жидкости, а приемник — в исследуемой, обе жидкости разделяет акустически прозрачное окно. При такой схеме изменяются лишь расстояния, проходимые акустическими импульсами в обеих средах. Это исключает влияние отражений волны и других нежелательных эффектов на результаты измерений коэффициента затухания. Относительная погрешность измерений при использовании таких устройств не превышает ±2%. Определенные трудности возникают в тех случаях, когда исследуются не жидкости, а биологические ткани. Однако эти трудности можно преодолеть [177], если изготовить из биологической ткани «фарш», коэффициент затухания в котором, по-видимому, не слишком отличается от коэффициента затухания исходной ткани. Дополнительные трудности связаны с необходимостью использования образцов очень большого объема (1—4 л).
Более широкое распространение получил метод введения образца, который оказался более пригодным для измерений затухания в биологических тканях. Он основан на вычислении логарифма отношения амплитуд двух принятых сигналов, один из которых регистрируется при введении образца ткани между излучателем и приемником, а второй — при наличии только эталонной среды. Использование дополнительной эталонной среды в качестве буфера между преобразователями и образцом исследуемой ткани (рис. 4.5) приводит к снижению погрешностей измерения, обусловленных дифракционными потерями. Это достигается за счет уменьшения относительного изменения полной длины акустического пути сигнала при введении образца ткани. Такой принцип применим также к измерительным системам других типов (обсуждаемым ниже), и мы будем основываться на этом принципе при общем анализе погрешностей измерений затухания звука. К недостаткам метода введения образца следует отнести влияние отражений от поверхностей образца, которые вносят определенный вклад в величину измеренных потерь. Большие трудности возникают также при изготовлении образцов биологических тканей со строго параллельными поверхностями. Погрешность измерений с помощью данного метода составляет обычно ± 10% или даже большую величину. Отчасти ситуация может быть улучшена, и влияние потерь на отражение можно автоматически исключить, если провести серию измерений на образцах одного и того же материала различной толщины. В этом случае коэффициент определяется по наклону кривой, характеризующей зависимость затухания от толщины образца.
К классу узкополосных систем относятся также различные измерительные устройства, в которых используются непрерывные волны и резонансные явления. Сюда входят интерферометрические и реверберационные устройства.
Ультразвуковые интерферометры делятся на интерферометры с переменной базой ([43, 126], см. также ссылки, указанные в начале разд. 4.4.1) и интерферометры с перестраиваемой частотой [58, 89].
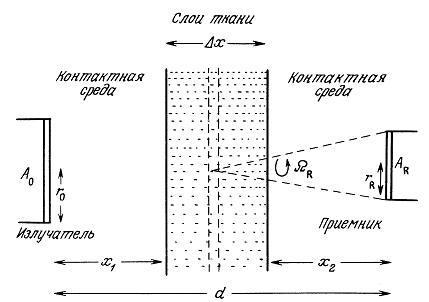
Рис. 4.5. Типичная схема экспериментальной установки для измерений затухания звука по методу введения образца, который широко используется для исследования «твердых» биологических тканей. Подобные системы могут быть широкополосными или узкополосными. Приемный элемент либо может быть фазочувствительным, либо может реагировать на мощность излучения. Иногда вместо приемника используется широкоапертурный плоский рефлектор, отражающий падающую звуковую волну в обратном направлении к излучателю.
В обоих случаях обеспечивается резонансное расстояние между излучающим и приемным преобразователями или между излучающим преобразователем и плоским отражателем. Искомая длина волны и соответственно фазовая скорость звука определяются по расстоянию или по разности частот между отдельными резонансными пиками. Коэффициент затухания можно найти, измеряя зависимость амплитуды резонансных пиков от расстояния или ширину этих пиков. В общем случае на результаты измерений существенно влияют дифракционные эффекты и переотражения на боковых стенках камеры интерферометра. Поэтому интерферометрические методы не являются абсолютными и требуют калибровки по жидкости с известными акустическими свойствами. Тем не менее они обеспечивают возможность измерений в широкой полосе частот при малых объемах исследуемой среды. Так, в интерферометре Эггерса требуемый для измерений объем исследуемой жидкости составлял всего 10 мл 1), а диапазон рабочих частот варьировался в пределах от 0,2 до 10 МГц.
1) Рабочий объем интерферометров Эггерса в ряде вариантов не превышал 1 мл. — Прим. ред.
Такой интерферометр использовался Госсом и Данном [83] для измерений затухания звука в суспензиях коллагена в диапазоне частот 0,5—3 МГц. Расчетная погрешность измерений составляла при этом ±10%.
Принцип действия реверберационных систем (см. ссылки, цитируемые в начале разд. 4.4.1) основан на измерении скорости затухания ультразвуковых колебаний в сравнительно большой и почти не имеющей потерь резонансной камере, содержащей исследуемую жидкость. В качестве такой камеры используется, например, пятилитровая тонкостенная сфера из стекла, находящаяся в вакууме. Измерения проводятся после выключения источника звука, причем скорость затухания колебаний определяется главным образом коэффициентом затухания исследуемой жидкости. Хотя в этом случае дифракционные потери отсутствуют, необходимо вводить поправки на потери в стенках камеры. Эти поправки определяются по результатам измерений затухания в какой-либо эталонной жидкости, акустический импеданс которой равен импедансу исследуемой жидкости. Таким образом, реверберационные методы также не дают абсолютных значений![]() . Рабочие частоты лежат в области ниже 1 МГц.
. Рабочие частоты лежат в области ниже 1 МГц.
При использовании пьезоэлектрических преобразователей в качестве приемников для измерений затухания звука в неоднородных средах возникают артефакты, известные под названием погрешностей «фазовой компенсации» (см. разд. 4.4.2.3). В тех узкополосных системах, где применяются не чувствительные к фазе приемники, реагирующие на мощность излучения, этот источник погрешностей отсутствует. Обычно используется метод введения образца и роль эталонной жидкости играет вода. В качестве устройств, реагирующих на мощность излучения, широко применяются радиометры, измеряющие радиационное давление [38, 118, 142, 175, 183, 184]. При работе с такими приборами необходимо исключить погрешности, связанные с ультразвуковой дегазацией образца и контактной жидкости, с акустическими течениями в контактной жидкости, а также с изменением плавучести мишени радиометра под действием ультразвукового нагрева. Тем не менее было показано, что метод радиационного давления дает наиболее согласующиеся и точные данные о затухании звука в тканях млекопитающих. Сами по себе акустические течения можно было бы использовать для измерений а в широкой полосе частот, но этому препятствует необходимость работать с очень большими объемами жидкости с известной вязкостью [21, 93]. В качестве приемников, чувствительных к мощности излучения, применяются также и термоэлектрические датчики [76, 77]. Так, например, Данн и Фрай [52] использовали такие датчики для измерения затухания звука в легких. Маркус и Карстенсен [142] указывали на перспективность акустоэлектрических приемников из сульфида кадмия, которые могут быть использованы для измерения полной мощности ультразвукового излучения в импульсном режиме. Миллер и др. [150], а также Бюссе и Миллер [26] воспользовались этой идеей и разработали подобные акустоэлектриче-ские приемники (не чувствительные к фазе) специально для измерений затухания звука в мышечной ткани.
Б. Широкополосные системы. В последние годы вслед за применением методов спектрального анализа в задачах неразрушающего контроля был разработан ряд устройств, в которых широкополосные зондирующие акустические сигналы использовались в сочетании с соответствующей обработкой сигналов приемника. Эти устройства позволяют получить непрерывную зависимость а от частоты без замены преобразователей [6, 16, 34, 67, 99, 102, 109, 130, 150, 174]. Такие возможности представляются весьма интересными, тем более, что в настоящее время при доступности компьютеров и устройств обработки высокочастотных сигналов разработка автоматизированной системы подобного типа не представляет особого труда. Действительно, широкополосные (спектральные) системы стали сейчас наиболее популярными для исследования акустических характеристик биологических тканей (во всех, кроме одной, из указанных выше речь идет именно о биологических тканях). Не следует, однако, недооценивать экспериментальные трудности, возникающие при реализации подобных систем. Кроме того, далек еще от завершения теоретический анализ погрешностей измерений, присущих устройствам для спектрального анализа. Весьма сложной является, например, задача создания действительно широкополосных систем. Наилучших результатов в этом плане добились, по-видимому, Бабу и др. [6]. С помощью одной пары преобразователей им удалось получить полосу частот от 1,5 до 11 МГц, но этому предшествовали длительные изыскания и проработки [124]. Чиверс и Хилл [34] показали, что при использовании современных диагностических преобразователей для перекрытия диапазона частот от 1 до 7 МГц потребуется пять таких преобразователей. В течение долгого времени работа Пападакиса и др. [174] оставалась единственной работой, посвященной строгому анализу погрешностей широкополосных методов, связанных с дифракционными потерями. В последнее время этим вопросам вновь стало уделяться большое внимание в связи с измерениями затухания звука в биологических тканях in vivo (см. разд. 4.4.2.2). При использовании спектральных методов обработки принятых сигналов для сохранения полной информации, заложенной в высокочастотном сигнале, требуется, чтобы приемники звука были чувствительны не только к амплитуде, но и к фазе сигнала. В случае применения фазочувствительных приемников неизбежно возникают уже упомянутые ранее артефакты, связанные с эффектами компенсации фазы. Однако в дальнейшем будет показано, что спектральный анализ позволяет легко распознать наличие этих эффектов. Решение такой проблемы облегчается, в частности, при использовании методов спектрального усреднения и интерполирования. Подобные возможности отсутствуют в рассмотренных ранее импульсных методах.
Во всех упомянутых широкополосных системах исследование образцов биологических тканей проводится на основе метода введения образца. Для обеспечения хорошего акустического контакта в качестве контактной среды используется вода или физиологический раствор. Обычно применяется либо схема с двумя преобразователями, либо схема с одним приемоизлучающим преобразователем и плоским отражателем. Принятые ультразвуковые импульсы преобразуются в спектр акустических частот и зависимость а от частоты определяется на основе измерения логарифмов отношения амплитуд соответствующих спектральных компонент, полученных при введении исследуемого образца ткани и при его отсутствии. За единственным исключением, во всех системах предусмотрена возможность того, чтобы излучаемые акустические импульсы содержали по возможности наименьшее число периодов высокочастотных колебаний. Спектральный анализ принятых сигналов выполняется либо с помощью аналогового высокочастотного спектроанализатора, либо на основе предварительного цифрового преобразования импульса с последующим машинным расчетом его спектра, который осуществляется с помощью алгоритма дискретного фурье-преобразования. Второй способ позволяет сохранить фазовую информацию с целью определения дисперсии скорости звука, однако в зависимости от типа применяемого компьютера его возможности могут быть ограничены по быстродействию, динамическому диапазону и интервалу рабочих частот. Исключение в этом плане представляет спектрометрическая система с временной задержкой, которую Хейсер и Круазетт [99] первоначально разработали для получения изображений в трансмиссионном режиме. В этой системе, реализующей метод введения образца, через среду пропускается сигнал качающейся частоты (частотно-модулированный сигнал), который затухает и задерживается по времени при прохождении через исследуемый образец. Путем гетеродинирования принятого и излученного сигналов формируется сигнал звуковой частоты, амплитуда которого связана с затуханием в образце, а частота зависит от временной задержки, иными словами, от скорости звука в образце.
В. Получение пространственных распределений затухания. До сих пор в данном разделе мы рассматривали методы измерений, на основе которых можно определить акустические параметры ткани, усредненные по пути прохождения ультразвуковой волны. Однако часто требуется измерить пространственное распределение этих параметров по всему объему исследуемого образца. Такая задача возникает, например, когда необходимо провести сравнение участков нормальной ткани с теми областями, где замечены какие-либо патологические изменения. Одно из возможных решений поставленной задачи заключается в использовании систем, в которых предусмотрена возможность сканирования по пространству. Существуют, однако, системы совершенно другого типа, в которых результаты измерений воспроизводятся в виде изображений. Так, например, в системе Кальдерона и др. [27] пространственная картина затухания звука в исследуемом образце визуализируется по результатам измерения амплитуды смещения тонкой мембраны, приводимой в колебание коротким (с шириной полосы 1,5—3 МГц) акустическим импульсом, прошедшим через образец. Амплитуда смещения мембраны измеряется с помощью сканирующего лазерного интерферометра. Следует отметить, что погрешности измерений затухания с помощью такой системы могут быть весьма значительными, однако их строгий анализ не проводился.
Изображения распределений коэффициента затухания звука в плоскости зондирующего ультразвукового пучка в принципе можно получить на основе компьютерной реконструкции по одномерным акустическим проекциям. Однако в настоящее время погрешности такого метода, обусловленные рефракцией звука и эффектом компенсации фаз, настолько велики, что скорость звука является, по-видимому, единственным параметром, изменения которого могут быть визуализированы таким способом с приемлемой точностью [29, 91, 114].
Недавно Фостер и др. [68] разработали устройство, которое они назвали ультразвуковым макроскопом. Составными элементами этого устройства являются одиночный сильно фокусирующий преобразователь, работающий в режимах излучения и приема, и плоский отражатель, установленный в фокальной плоскости преобразователя. Используя метод введения образца, авторы применили подобное устройство для визуализации и количественной оценки распределения затухания и скорости звука в образцах удаленной молочной железы на частоте 13 МГц. Для получения пространственных распределений коэффициента затухания с успехом могут быть использованы акустические микроскопы, работающие на высоких частотах и обладающие высокой разрешающей способностью. О них речь пойдет ниже.
Г. Акустическая микроскопия. Измерения коэффициента затухания в тонких образцах биологических тканей (толщиной 0,3—2,5 мм) проводились с помощью растрового лазерного акустического микроскопа [ПО], работающего на частоте 100 МГц. При этом использование набора образцов различной толщины позволило снизить погрешность определения усредненной величины затухания до уровня ±5°7о [196, 197]. Более подробно проблемы акустической микроскопии рассматриваются в гл. 9.
4.4.1.3. Измерения in vivo
Мы уже отмечали, что метод нестационарного нагрева, основанный на использовании термоэлектрических датчиков, позволяет провести точные измерения поглощения звука в биологических тканях in vivo. Измерения коэффициента затухания в живых тканях также возможны, однако приемлемая точность таких измерений может быть достигнута только при определенных условиях. Так, например, в случае молочной железы in vivo [67] эти условия сводятся к возможности реализации трансмиссионного режима, т. е. к установке излучающего и приемного преобразователей на противоположных поверхностях данного органа с целью измерения коэффициента затухания а, усредненного по пути прохождения ультразвука. Вообще говоря, для тех анатомических структур, которые допускают возможность подобных измерений в трансмиссионном режиме in vivo, с помощью методов реконструктивной томографии [91] можно получить количественные оценки локальных значений ![]() .
.
Все другие методы измерений in vivo, разработанные к настоящему времени, дают по существу статистические оценки а. В основе этих методов лежит одно или несколько допущений относительно характера распространения и рассеяния акустических волн в исследуемой ткани.
Если эти характеристики приблизительно постоянны и одинаковы в пределах исследуемой области ткани и если эта область сравнительно велика (как, например, в случае цирроза печени), то достаточно хорошие оценки среднего коэффициента затухания акустического импульса можно получить на основе обработки результатов измерения амплитуд эхо-сигналов по методу экспоненциальной регрессии [156, 157].
В работе [176] проведен дальнейший обстоятельный анализ этого метода. Он был применен для обработки первичных данных измерений, полученных с помощью системы ультразвукового Всканирования. Эти данные корректировались с учетом нелинейной характеристики устройства обработки сигналов. В результате была получена частотная зависимость коэффициента затухания звука.
Для оценки углового наклона кривой зависимости а. от частоты можно применить метод спектрального анализа последовательности эхо-импульсов. Такой подход становится возможным в тех случаях, когда частотная зависимость затухания звука постоянна в исследуемом диапазоне частот, излучаемый акустический импульс имеет гауссову форму и рассеивающие свойства биологической ткани на макроскопическом уровне одинаковы по всему исследуемому объему ткани [123]. Зависимость коэффициента затухания от частоты приводит к понижению центральной частоты в спектре акустического импульса по мере его распространения в среде. При этом, если указанные выше допущения справедливы, такое смещение зависит линейно от пройденного пути. За последние годы эта идея получила дальнейшее развитие, что привело к обобщению теории на те случаи, когда форма зондирующих импульсов отличается от гауссовой, а зависимость а от частоты нелинейна [159, 170, 192]. Достигнутые успехи позволили упростить метод определения частотного смещения в спектре импульса [66], скомпенсировать влияние ^дифракционного поля преобразователя (см. разд. 4.4.2.2) и провести клиническую апробацию спектрального метода на серийной аппаратуре. В работе [141] приводятся предварительные результаты клинических испытаний in vivo. Лиман и. др. [129] провели сравнительный анализ большинства предложенных методов измерения затухания звука in vivo.
Лицци и др. [135] применили пространственное усреднение спектров эхо-сигналов по направлению распространения ультразвукового пучка и перпендикулярно к нему для расчета зависимости а от частоты (см. гл. 10). Отметим, что выдвигались также идеи о возможности раздельного измерения in vivo пространственных распределений коэффициента затухания и сечения обратного рассеяния единичного объема ткани. Такая возможность открывается на основе применения цифровой реконструкции обратного рассеяния [41] (см. также гл. 9) без учета дифракционных явлений и в предположении об изотропности обратного рассеяния и других характеристик распространения ультразвука. Этот метод подразумевает также использование набора частиц [100, 132]. Он представляет собой по существу метод реконструкции, в рамках которого для описания частотных зависимостей затухания и рассеяния используются достаточно простые функции.
4.4.2. ПРОБЛЕМЫ, СВЯЗАННЫЕ С АРТЕФАКТАМИ И ПОГРЕШНОСТЯМИ ИЗМЕРЕНИЙ
Погрешности измерений затухания звука могут быть вызваны самыми различными причинами, многие из которых трудно установить с достаточной надежностью. Если, кроме того, учесть большое разнообразие применяемых методов измерений, то станет понятно, что невозможно проанализировать все возможные источники ошибок измерения. Поэтому в дальнейшем мы ограничимся рассмотрением только широко применяемого метода введения образца (см. рис. 4.5) и некоторое внимание уделим методу спектрального анализа, поскольку для него анализ погрешностей проводился в гораздо меньшей степени, чем для других методов.
Прежде всего мы получим расчетные формулы, которыми обычно пользуются для определения затухания. Затем будут рассмотрены источники погрешностей измерений и их относительный вклад. При этом основное внимание мы уделим тем первичным источникам погрешностей, которые существуют даже в случае однородных сред. Далее мы перейдем к более сложному случаю реальных, т. е. неоднородных биологических тканей и исследуем влияние способов подготовки образца и условий измерения.
4.4.2.1. Расчетные формулы
При использовании схемы измерения, показанной на рис. 4.5, акустическая мощность регистрируемого приемником сигнала при отсутствии образца исследуемой ткани на пути волны определяется выражением

где ![]() — акустическая мощность сигнала на излучателе, ST — площадь приемника,
— акустическая мощность сигнала на излучателе, ST — площадь приемника, ![]() — коэффициент затухания по интенсивности в контактной среде, d — расстояние между излучателем и приемником, G — коэффициент усиления. В том случае, когда приемник малых размеров находится в дальней зоне излучателя, G представляет собой величину, на которую следует умножить значение интенсивности изотропного излучения, чтобы получить реальную интенсивность с учетом направленности излучателя (для излучателя с большой площадью активной поверхности S0
— коэффициент затухания по интенсивности в контактной среде, d — расстояние между излучателем и приемником, G — коэффициент усиления. В том случае, когда приемник малых размеров находится в дальней зоне излучателя, G представляет собой величину, на которую следует умножить значение интенсивности изотропного излучения, чтобы получить реальную интенсивность с учетом направленности излучателя (для излучателя с большой площадью активной поверхности S0 ![]() . Если же приемник не отодвинут глубоко в дальнюю зону излучателя, то в коэффициент G включаются также дифракционные поправки.
. Если же приемник не отодвинут глубоко в дальнюю зону излучателя, то в коэффициент G включаются также дифракционные поправки.
При введении в ультразвуковой пучок образца биологической ткани акустическая мощность регистрируемого приемником сигнала будет равна
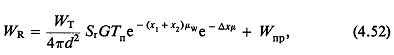
где Тп — коэффициент прохождения (по энергии) через границу между контактной средой и биологической тканью, ![]() — искомый коэффициент затухания звука,
— искомый коэффициент затухания звука, ![]() : — толщина исследуемого образца ткани, х1 и Х2 — расстояния до образца соответственно от излучателя и приемника (рис. 4.5), Wnp— мощность рассеянного тканью излучения на приемнике, т. е. мощность рассеянного излучения в направлении распространения акустической волны. Выражение (4.52) получено без учета многократного рассеяния в предположении, что скорость звука в контактной среде и образце ткани одинакова. На основе интегрирования рассеяния в прямом направлении по пути прохождения волны в образце Бэмбер [7] получил следующее выражение для мощности на приемнике:
: — толщина исследуемого образца ткани, х1 и Х2 — расстояния до образца соответственно от излучателя и приемника (рис. 4.5), Wnp— мощность рассеянного тканью излучения на приемнике, т. е. мощность рассеянного излучения в направлении распространения акустической волны. Выражение (4.52) получено без учета многократного рассеяния в предположении, что скорость звука в контактной среде и образце ткани одинакова. На основе интегрирования рассеяния в прямом направлении по пути прохождения волны в образце Бэмбер [7] получил следующее выражение для мощности на приемнике:
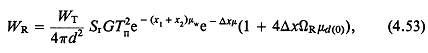
где ![]() — телесный угол, образованный лучами, проведенными из центра образца к граничной окружности приемника,
— телесный угол, образованный лучами, проведенными из центра образца к граничной окружности приемника, ![]() — дифференциальное сечение рассеяния единичного объема образца в направлении распространения падающей волны. Это выражение получено в приближении однократного рассеяния при условии, что толщина образцов мала и образцы находятся в однородном поле вдали от приемника.
— дифференциальное сечение рассеяния единичного объема образца в направлении распространения падающей волны. Это выражение получено в приближении однократного рассеяния при условии, что толщина образцов мала и образцы находятся в однородном поле вдали от приемника.
Измерения величины ![]() в биологических тканях не проводились. Расчетные значения этой величины для различных тканей и частот ультразвука, полученные путем экстраполяции результатов измерений дифференциального сечения рассеяния под другими углами [28], различаются на несколько порядков. В сочетании с огромным числом возможных модификаций измерительных схем это означает, что в настоящее время невозможно рассчитать вероятный вклад рассеяния в прямом направлении в величину измеряемого затухания звука. Можно лишь показать, что при определенных условиях вклад прямого рассеяния в мощность регистрируемого приемником акустического сигнала будет весьма существенным. Так, например, по данным Нассири и Хилла [161], значение
в биологических тканях не проводились. Расчетные значения этой величины для различных тканей и частот ультразвука, полученные путем экстраполяции результатов измерений дифференциального сечения рассеяния под другими углами [28], различаются на несколько порядков. В сочетании с огромным числом возможных модификаций измерительных схем это означает, что в настоящее время невозможно рассчитать вероятный вклад рассеяния в прямом направлении в величину измеряемого затухания звука. Можно лишь показать, что при определенных условиях вклад прямого рассеяния в мощность регистрируемого приемником акустического сигнала будет весьма существенным. Так, например, по данным Нассири и Хилла [161], значение ![]() для печени на частоте 6 Мгц может достигать
для печени на частоте 6 Мгц может достигать ![]() . При этом, если в качестве геометрического множителя
. При этом, если в качестве геометрического множителя ![]() взять достаточно большое, но реальное значение
взять достаточно большое, но реальное значение ![]() /8, то член, стоящий в скобках в формуле (4.53), будет приблизительно равен
/8, то член, стоящий в скобках в формуле (4.53), будет приблизительно равен ![]() . Другими словами, в данном гипотетическом случае относительная погрешность, возникающая из-за пренебрежения вкладом прямого рассеяния в мощность регистрируемого сигнала, составляет примерно 20%.
. Другими словами, в данном гипотетическом случае относительная погрешность, возникающая из-за пренебрежения вкладом прямого рассеяния в мощность регистрируемого сигнала, составляет примерно 20%.
Если все же пренебречь прямым рассеянием, то, деля выражение (4.51) на (4.52) и проводя логарифмирование, можно получить
![]()
Для случая, когда вместо приемника используется плоский отражатель, аналогичным образом получаем
![]()
Обычно величинами Тп и ![]() пренебрегают и считают, что отношение
пренебрегают и считают, что отношение ![]() в зависимости от частоты определяется квадратом отношения амплитуд соответствующих электрических сигналов
в зависимости от частоты определяется квадратом отношения амплитуд соответствующих электрических сигналов ![]() и
и ![]() . Это дает
. Это дает
![]()
В случае применения аналоговых спектральных методов величины ![]() и
и ![]() определяются по спектрам, представленным в логарифмическом масштабе соответственно при наличии исследуемого образца и при его отсутствии.
определяются по спектрам, представленным в логарифмическом масштабе соответственно при наличии исследуемого образца и при его отсутствии.
4.4.2.2. Погрешности измерений в однородных средах
Если на время пренебречь неоднородностями акустических свойств биологических тканей, то можно оценить основные источники погрешностей, связанные с измерением величин, стоящих в правой части выражения (4.56). Прежде всего отметим, что изготовление исследуемого образца в виде плоского слоя постоянной толщины не вызывает затруднений в случае твердых тел или жидкостей, однако в случае мягких биологических тканей очень не просто получить слой постоянной толщины, отклонения от которой составляли бы менее ±10%. В противоположность этому при принятии надлежащих мер несложно обеспечить высокую точность измерения амплитуд сигналов ![]() и V. Для этой цели необходимо использовать широкополосные калиброванные аттенюаторы, обеспечивающие возможность работы на линейном участке характеристики усилителя принимаемых сигналов при измерениях как в эталонной среде, так и в исследуемой ткани. При этом точность измерения величин
и V. Для этой цели необходимо использовать широкополосные калиброванные аттенюаторы, обеспечивающие возможность работы на линейном участке характеристики усилителя принимаемых сигналов при измерениях как в эталонной среде, так и в исследуемой ткани. При этом точность измерения величин ![]() и V ограничивается точностью калибровки аттенюатора и усилителей (в зависимости от частоты), а также погрешностью цифрового преобразования (числом бит) в случае машинной обработки. При использовании измерительных систем с отражателями могут потребоваться высокочастотные стробирующие усилители, которые также должны быть откалиброваны. Все это приводит к ограничению возможностей подавления паразитных сигналов, связанных, например, с мощным сигналом возбуждения излучателя, т. е. к ограничению динамического диапазона измерительной системы. Следует также учитывать, что точность воспроизведения спектров исследуемых сигналов в логарифмическом масштабе в случае аналоговых спектроанализаторов обычно не превосходит ±(0,2 — 0,3) дБ. Анализ выражения (4.56) показывает, что определенные требования должны предъявляться к частоте, на которой проводятся измерения. В частности, если исследуется непрерывная зависимость затухания от частоты, то погрешность измерения частоты будет приводить к определенной погрешности измерения величин
и V ограничивается точностью калибровки аттенюатора и усилителей (в зависимости от частоты), а также погрешностью цифрового преобразования (числом бит) в случае машинной обработки. При использовании измерительных систем с отражателями могут потребоваться высокочастотные стробирующие усилители, которые также должны быть откалиброваны. Все это приводит к ограничению возможностей подавления паразитных сигналов, связанных, например, с мощным сигналом возбуждения излучателя, т. е. к ограничению динамического диапазона измерительной системы. Следует также учитывать, что точность воспроизведения спектров исследуемых сигналов в логарифмическом масштабе в случае аналоговых спектроанализаторов обычно не превосходит ±(0,2 — 0,3) дБ. Анализ выражения (4.56) показывает, что определенные требования должны предъявляться к частоте, на которой проводятся измерения. В частности, если исследуется непрерывная зависимость затухания от частоты, то погрешность измерения частоты будет приводить к определенной погрешности измерения величин ![]() или V, причем величина этой погрешности зависит от углового наклона кривой, характеризующей частотную зависимость амплитуды принятого сигнала. Поэтому желательно, чтобы измерительная система имела по возможности равномерную амплитудно-частотную характеристику во всем диапазоне исследуемых частот. Длина кодовой последовательности в случае цифровых устройств, длительность сигнала или стробирующего импульса, а также характеристики фильтра в случае аналоговых устройств — все эти параметры помимо выбранного масштаба частот или скорости цифрового преобразования оказывают влияние на разрешающую способность по частоте всей системы. Паразитные скачки напряжения, возникающие при включении или выключении аналоговых схем стробирования, будут интерферировать с принятым импульсным сигналом. Это приводит к модуляции частотного спектра сигнала, причем такая модуляция зависит от временных соотношений между регистрируемым сигналом и стробирующим импульсом.
или V, причем величина этой погрешности зависит от углового наклона кривой, характеризующей частотную зависимость амплитуды принятого сигнала. Поэтому желательно, чтобы измерительная система имела по возможности равномерную амплитудно-частотную характеристику во всем диапазоне исследуемых частот. Длина кодовой последовательности в случае цифровых устройств, длительность сигнала или стробирующего импульса, а также характеристики фильтра в случае аналоговых устройств — все эти параметры помимо выбранного масштаба частот или скорости цифрового преобразования оказывают влияние на разрешающую способность по частоте всей системы. Паразитные скачки напряжения, возникающие при включении или выключении аналоговых схем стробирования, будут интерферировать с принятым импульсным сигналом. Это приводит к модуляции частотного спектра сигнала, причем такая модуляция зависит от временных соотношений между регистрируемым сигналом и стробирующим импульсом.
Ко второй группе погрешностей следует отнести погрешности, возникающие в тех случаях, когда нарушаются допущения, сделанные при выводе выражения (4.56). В этом плане мы рассмотрим, во-первых, справедливость предположения о линейности распространения ультразвуковых волн и линейности электроакустического преобразования. Во-вторых, мы проанализируем, к чему приводит пренебрежение эффектами прямого рассеяния и отражения на граничных поверхностях биологической ткани, а также пренебрежение затуханием в объеме контактной жидкости, вытесненной образцом ткани. В-третьих, будут рассмотрены проблемы, связанные с предположением о равенстве скорости звука в контактной среде и исследуемом образце ткани.
Влияние нелинейного характера распространения ультразвука на результаты измерений затухания подробно рассматривалось в разд. 4.3.8. Хотя влияние нелинейных эффектов может быть уменьшено посредством правильного размещения образца (вне области стабилизации), все же следует стремиться к тому, чтобы нелинейные эффекты вообще не возникали и можно было пользоваться линейным приближением. Линейность распространения волн и линейность электроакустического преобразования проверяются достаточно просто. Для этого снимается зависимость результатов измерений от амплитуды входного напряжения, подаваемого на излучатель. Следует отметить, что артефакты, связанные с нелинейностью распространения волн, будут проявляться, по всей видимости, наиболее заметно в широкополосных спектральных системах измерений при использовании коротких импульсов с высокими пиковыми значениями амплитуды давления. Акияма и др. [3] специально исследовали эту проблему на основе компьютерного моделирования с применением низкочастотной фильтрации. На основе выражения, аналогичного формуле (4.44), они рассчитали изменение формы короткого импульса по мере его распространения в измерительной системе типа той, которая показана на рис. 4.5. Оказалось, что по мере возрастания пиковой амплитуды давления погрешности измерения возникают прежде всего на самых верхних и самых нижних частотах спектра излучаемого преобразователем сигнала. На этих частотах получались заниженные значения коэффициента затухания. Какого-либо объяснения подобного эффекта не было дано.
Исходя из значений удельных акустических импедансов воды и мягких тканей (см. гл. 1), можно рассчитать соответствующий коэффициент прохождения Гп, который в данном случае равен приблизительно 0,997. Пренебрежение этой величиной приводит к несколько завышенным значениям затухания звука, однако подобная погрешность не превышает 0,05 дБ даже в случае систем с отражателями (см. (4.55)). Как правило, акустические окна, разделяющие исследуемый образец и контактную среду, изготавливаются из полиэтилена, майлара, сарана и подобных им полимерных материалов. Бэмбер [7] исследовал затухание звука в монослое полиэтилена толщиной 25 мкм в частотном диапазоне 2—10 Мгц и получил, что эта величина составляет приблизительно 0,005 дБ-МГц-1,2. В системах с отражателями подобные потери не превышают 1—2% от величины измеряемого затухания. Поэтому при исследовании мягких биологических тканей потери, вызванные отражениями волн на границах раздела, часто не учитываются. Для тех сред, где измеряемый коэффициент затухания мал (например, в семенниках или в биологических жидкостях типа крови) или велики потери на отражение (как, например, в костях или некоторых фантомах, моделирующих биологическую ткань), можно использовать линейную аппроксимацию зависимости затухания от толщины образца при измерениях на различных образцах одного и того же материала, что позволяет учесть потери на отражение в виде некоторой постоянной поправки.
Если в качестве контактной среды используется вода, то на частоте 1 МГц значение ![]() составляет примерно 0,002 дБ/см. Эта величина растет пропорционально квадрату частоты f2, однако даже на частоте 8 МГц ее значение не превышает 0,14 дБ/см. Для повышения точности измерений на высоких частотах в средах с малым затуханием можно воспользоваться значениями
составляет примерно 0,002 дБ/см. Эта величина растет пропорционально квадрату частоты f2, однако даже на частоте 8 МГц ее значение не превышает 0,14 дБ/см. Для повышения точности измерений на высоких частотах в средах с малым затуханием можно воспользоваться значениями ![]() полученными Пинкертоном [181] для дегазированной дистиллированной воды при различных температурах и частотах.
полученными Пинкертоном [181] для дегазированной дистиллированной воды при различных температурах и частотах.
При измерениях на печени пренебрежение вкладом прямого рассеяния в энергию регистрируемого приемником сигнала приводило к заниженным оценкам коэффициента затухания а, которые отличались от реальных значений на некоторую неизвестную величину. Очевидно, что такая погрешность наиболее существенна при исследовании сред с сильным рассеянием (таких, как легкие, кости и, возможно, молочная железа). Другими словами, для тех сред, где ![]() дает заметный вклад в
дает заметный вклад в ![]() , применение различных измерительных систем может привести к получению разных значений а в зависимости от таких факторов, как толщина образца, расстояние от образца до приемника и площадь поверхности приемника. Возможно, что особое внимание в этом плане следует уделять материалам для фантомов, моделирующих биологические ткани по затуханию и скорости звука. Обычно фантомы состоят из основы с очень низким значением
, применение различных измерительных систем может привести к получению разных значений а в зависимости от таких факторов, как толщина образца, расстояние от образца до приемника и площадь поверхности приемника. Возможно, что особое внимание в этом плане следует уделять материалам для фантомов, моделирующих биологические ткани по затуханию и скорости звука. Обычно фантомы состоят из основы с очень низким значением ![]() , к которой добавляется то или иное количество порошкообразного графита, обеспечивающее требуемое значение
, к которой добавляется то или иное количество порошкообразного графита, обеспечивающее требуемое значение ![]() .
.
Различие в скорости звука между исследуемой тканью и контактной средой приводит по крайней мере к трем возможным источникам погрешности измерений. К ним относятся объемная рефракция ультразвукового пучка, обусловленная угловым смещением образца или непараллельностью его поверхностей, дифракционные потери, а также эффект компенсации фазы, возникающий в результате вариаций пути прохождения в пределах ширины пучка. Вообще говоря, погрешности, связанные с рефракцией, снижаются при использовании фокусирующих преобразователей, тонких образцов, приемников с большой апертурой, а также при уменьшении расстояния между образцом ткани и приемником. Кроме того, эти погрешности менее существенны при использовании отражателей по сравнению со случаем, когда применяются два преобразователя. По оценкам Бэмбера [7], погрешность измерения затухания, обусловленная объемной рефракцией, не превышает 1% при использовании схемы с отражателем и при условии, что непараллельность поверхностей образца и его отклонение от оси зондирующего пучка лежат в пределах ±3°.
В некоторых измерительных системах с переменным расстоянием пренебрежение потерями, связанными с дифракционными эффектами в поле излучателя, может привести к погрешности, достигающей 30%. На рис. 4.6, а представлены расчетные величины полных дифракционных потерь при различных расстояниях от поверхности излучателя [191]. В расчетах предполагалось, что интенсивность пропорциональна квадрату звукового давления, усредненного по поверхности приемника. Интенсивность принятого сигнала вычислялась для различных расстояний Z, выраженных в единицах ![]() (г— радиус преобразователя), при условии, что форма и площадь поверхности приемника и излучателя одинаковы и что оба преобразователя расположены соосно.
(г— радиус преобразователя), при условии, что форма и площадь поверхности приемника и излучателя одинаковы и что оба преобразователя расположены соосно.
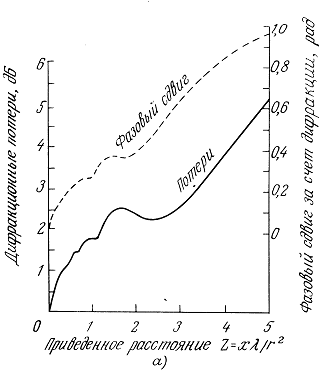
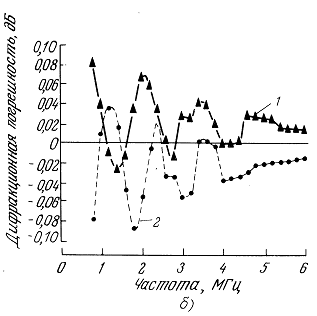
Рис. 4.6. а — Дифракционные потери и фазовый сдвиг при использовании круглого поршневого излучателя радиусом r [191, 171]; б — дифракционная погрешность (т. е. дополнительное затухание), найденная по данным а в случае применения измерительной схемы введения образца с фиксированным расстоянием и перестраиваемой частотой (рис. 4.5); 1 — образец со скоростью звука 1600 м/с, 2 — образец со скоростью звука 1350 м/с. Скорость звука в контактной жидкости 1485 м/с, толщина образца 3 см, радиусы излучателя и приемника 7,5 мм. Приемник удален от излучателя на расстояние d, соответствующее последнему осевому максимуму поля излучателя.
Следует отметить, что использование метода введения образца позволяет свести к минимуму различия в длинах акустического пути, возникающие при измерениях сначала на эталонном, а затем на исследуемом образцах. Кроме того, если применяются системы с фиксированной частотой, то погрешность, обусловленную этими различиями в длине пути акустической волны, можно снизить еще больше, размещая приемник в областях локализации одного из дифракционных максимумов или минимумов. Это гарантирует, что небольшое смещение по координате Z вызовет лишь очень незначительное изменение дифракционных потерь. В случае применения двух коаксиальных фокусирующих преобразователей эта операция сводится к такому размещению приемного преобразователя, когда его фокальная область совмещается с фокальной областью излучателя [179]. Системы с перестраиваемой частотой, в которых отсутствует выраженная фокусировка акустического пучка, не обладают подобными возможностями и, хотя соответствующие погрешности достаточно малы, интересно проследить их зависимость от частоты. На рис. 4.6, б представлены примеры частотной зависимости дополнительных потерь (или приращений) амплитуды регистрируемого сигнала, обусловленных различием в дифракционных потерях при наличии и отсутствии исследуемого образца в звуковом пучке (рис. 4.5). Графики получены для двух образцов с различной скоростью звука. В первом случае скорость звука составляла 1600 м/с, что соответствовало верхней границе значений скорости для биологических тканей типа печени. Во втором она равнялась 1350 м/с (очень низкое значение, характерное для жировой ткани). В обоих случаях скорость звука в контактной среде равнялась 1485 м/с, толщина образцов составляла 3 см, радиусы преобразователей — 7,5 мм, приемник устанавливался в области локализации последнего осевого максимума (Z = 1) в поле излучателя. На основе анализа представленных графиков можно выделить несколько характерных особенностей. Во-первых, дифракционные погрешности растут с понижением частоты. Во-вторых, периодический характер изменения этой систематической погрешности позволяет ее уменьшить путем аппроксимации экспериментальной кривой затухания некоторой сглаженной функцией частоты. В рассматриваемом случае в результате такой процедуры погрешность сводилась к постоянному значению, составляющему всего 0,03 дБ. В этом состоит преимущество использования систем с непрерывно перестраиваемой частотой над узкополосными системами, реализующими метод введения образца. В-третьих, если скорость звука в образцах превышает скорость звука в контактной среде, то дифракционные потери при усреднении приводят к отрицательным поправкам (т. е. действительно к потерям сигнала), тогда как при обратной ситуации получаются положительные поправки, т. е. усиление сигнала. В случае фокусированных преобразователей, установленных конфокально, независимо от соотношения скоростей звука в образце и контактной среде всегда имеют место дифракционные потери. И наконец, Пападакис [173], а также Брендел и Людвиг [25] показали, что минимумы и максимумы на кривой дифракционных потерь начинают сглаживаться по мере увеличения ширины полосы частот. Дифракционные потери также уменьшаются и сглаживаются при использовании аподизации излучающего преобразователя, когда амплитуда возбуждающих колебаний монотонно спадает вдоль радиуса излучателя от его центра к периферии [172] (см. также гл. 2).
Методам измерения коэффициента затухания in vivo, рассмотренным в разд. 4.4.1.3, также свойственны погрешности, связанные с дифракционными потерями или дифракционным усилением сигнала. Однако в данном случае ситуация чрезвычайно сложна и спектральные методы не позволяют провести точные оценки дифракционных поправок. Сложность заключается в необходимости рассмотрения «четырехмерного» (т. е. частотно-зависимого) дифракционного поля. Кроме того, не вполне определены свойства отражателей, по площади которых должно быть проинтегрировано данное дифракционное поле, а на величину дифракционных поправок для заданной точки поля оказывает влияние частотно-зависимое затухание в исследуемом образце. Различные подходы к решению этих проблем рассмотрены в работах [37, 64, 65, 105, 122, 165].
Ниже будет рассмотрен эффект компенсации фаз, который может возникнуть в однородных образцах в тех случаях, когда длина пути акустического пучка варьируется по его сечению.
Еще одним потенциальным источником погрешностей измерения является зависимость параметров среды от температуры и статического давления. Этот источник погрешностей детально исследован в физической акустике, однако он редко учитывался при измерениях в биологических средах. В частности, автору не известны какие-либо работы, посвященные исследованию зависимости коэффициента затухания от давления в биологических тканях. В случае жидкостей увеличение давления обычно приводит к уменьшению а. Так, например, для воды при изменении давления на одну атмосферу вариации а составляют примерно 25% при температуре 30 °С и достигают 64% при 0 °С [145]. Если предположить, что подобные количественные зависимости характерны и для биологических тканей, то изменения давления за счет погружения образцов ткани в воду или физиологический раствор на глубину порядка нескольких сантиметров (например, при изменении высоты раствора на ±8 см при 0°С) приводят к вариациям ![]() , не превышающим ±0,5%. Эти оценки вряд ли применимы к образцам, содержащим газ, поэтому подобные среды (в особенности ткани легкого) требуют специального исследования [52]. Бэмбер и Хилл [10] исследовали влияние зависимости
, не превышающим ±0,5%. Эти оценки вряд ли применимы к образцам, содержащим газ, поэтому подобные среды (в особенности ткани легкого) требуют специального исследования [52]. Бэмбер и Хилл [10] исследовали влияние зависимости ![]() от температуры на точность измерений затухания звука в мягких тканях. Наибольшие вариации наблюдались в случае жировой ткани при комнатной температуре, при этом величина
от температуры на точность измерений затухания звука в мягких тканях. Наибольшие вариации наблюдались в случае жировой ткани при комнатной температуре, при этом величина ![]() составляла около -5% при изменении температуры на один градус. Для обеспечения возможности сравнения различных данных необходимо, конечно, указывать точную температуру, при которой проводятся измерения, однако погрешности, вызванные небольшими колебаниями температуры, малы при 20 °С (например, их величина менее ±1% при изменениях температуры на ±0,2 °С) и близки к нулю при 37 °С.
составляла около -5% при изменении температуры на один градус. Для обеспечения возможности сравнения различных данных необходимо, конечно, указывать точную температуру, при которой проводятся измерения, однако погрешности, вызванные небольшими колебаниями температуры, малы при 20 °С (например, их величина менее ±1% при изменениях температуры на ±0,2 °С) и близки к нулю при 37 °С.
4.4.2.3. Влияние неоднородностей
В большинстве случаев акустические неоднородности биологических тканей являются причиной возникновения дополнительных погрешностей, связанных с рефракцией и дифракцией акустического поля в образце, а также с эффектом компенсации фаз при использовании фазочувствительных приемников. Наличие рефракции и дифракции в неоднородной среде может приводить к локальным возмущениям параметров ультразвукового пучка относительно тех их значений, которые наблюдались бы в данной точке приема, если бы единственным фактором, влияющим на ультразвуковой пучок, было затухание [67, 155]. По-видимому, никто пока еще не оценивал возможные величины этих погрешностей, хотя следует заметить, что они скорее всего будут существенными лишь при использовании приемников с очень малыми размерами.
Эффект компенсации фаз на приемнике может быть следствием различий либо в длине пути, либо в скорости звука на различных участках прохождения волны в среде с неоднородностями (рис. 4.7). При фиксированной частоте коэффициент затухания ![]() , связанный только с эффектом компенсации фаз, может быть рассчитан в явном виде. Для двух различных ситуаций, показанных на рис. 4.7, вклад этой величины в полное затухание а можно вычислить по формуле [7]
, связанный только с эффектом компенсации фаз, может быть рассчитан в явном виде. Для двух различных ситуаций, показанных на рис. 4.7, вклад этой величины в полное затухание а можно вычислить по формуле [7]
Рис. 4.7. Схематичное представление искажения фронта плоской волны после прохождения через образец из акустически неоднородного материала. Показаны два простейших примера влияния неоднородностей среды: а — скачок в толщине образца ![]() x(z) (толщина вдоль оси у неизменна); б — скачок скорости звука c1(z) (скорость вдоль оси у не меняется).
x(z) (толщина вдоль оси у неизменна); б — скачок скорости звука c1(z) (скорость вдоль оси у не меняется).
![]()
где g — относительная доля площади приемника, на которую падает часть волны с постоянной фазой (так, например, g = 0,5, если скачок фазы в волне делит площадь приемника точно пополам). Величина ![]() при наличии вариаций в длине пути определяется выражением
при наличии вариаций в длине пути определяется выражением
тогда как в случае вариаций скорости звука она равна
![]()
![]() — скорость звука в контактной среде. Расчетные значения
— скорость звука в контактной среде. Расчетные значения ![]() при различных значениях g и различных вариациях скорости звука и длины пути представлены на рис. 4.8. Видно, что даже сравнительно4 малые изменения в длине пути или скорости звука могут приводить к заметным погрешностям измерений, особенно на высоких частотах.
при различных значениях g и различных вариациях скорости звука и длины пути представлены на рис. 4.8. Видно, что даже сравнительно4 малые изменения в длине пути или скорости звука могут приводить к заметным погрешностям измерений, особенно на высоких частотах.
Рис. 4.8. Частотные зависимости дополнительного затухания принятого сигнала. Это затухание обусловлено эффектом компенсации фаз на поверхности круглого фазочувст-вительного приемника. Результаты расчетов при вариациях соответственно длины пути и скорости звука в случаях, показанных на рис. 4.7: а — номинальная толщина образца 4 см, на каждой кривой указано процентное отношение изменения толщины к полной толщине образца, значение g определяет ту часть площади приемника (относительно всей его площади), в пределах которой фазовый фронт падающей волны однороден; б — толщина образца 2,8 см и g = 0,1; на каждой кривой указана относительная разность (в процентах) скоростей звука в двух участках образца.
Миллер и др. [150] подробно исследовали влияние эффекта компенсации фаз на результаты измерения затухания в сердечной мышце собаки. В ряде случаев они получили завышенные оценки а, превосходящие реальные значения более чем на 100%. Маркус и Карстенсен [142] также отмечают, что при прохождении через мышечную ткань волна испытывает сильные фазовые вариации, тогда как в случае печени, заметных изменений фазы по сечению пучка не наблюдается. Результаты измерений коэффициента затухания а, выполненных в указанных двух работах с применением как пьезоэлектрических приемников, так и радиометров, хорошо согласовались в случае печени, однако в случае мышечной ткани их различие достигало 380%. Очевидно, что вклад эффекта компенсации фаз будет существенно изменяться при переходе от тканей одного типа к тканям другого и, возможно, при переходе от образца к образцу. О вариациях скорости звука в различных тканях и органах пока имеется очень немного данных. Необходимо отметить, однако, что с помощью широкополосных измерительных систем нетрудно распознать те неоднородные участки образца, в которых заметно проявляется эффект компенсации фаз и, следовательно, избежать их.
Рис. 4.9. Пример, характеризующий влияние эффекта компенсации фаз при измерениях затухания звука в свежеудаленной печени человека (длина пути 4,8 см). Импульсы а ид были зарегистрированы непосредственно перед исследуемой областью и за ней; импульс в наблюдался в пределах исследуемой области. Различие во временах прихода импульсов а и д вызывает интерференцию и компенсацию фаз на частоте около 3,5 МГц в спектре импульса г.
Такую возможность наглядно иллюстрирует рис. 4.9. Решению этой проблемы в определенной степени способствует также апостериорная обработка экспериментальных данных о затухании звука для фиксированных частот. Эта обработка заключается в усреднении и аппроксимации экспериментальных зависимостей сглаженными кривыми. Следует учитывать, что такая процедура неизбежно приводит к некоторому завышению коэффициента затухания и угла наклона частотной зависимости. Аналогичные проблемы, возникающие при измерениях рассеяния звука, будут рассмотрены в гл. 6.
Эффекты компенсации фаз можно свести к минимуму, если использовать не только не чувствительные к фазе приемники и широкополосные системы, но и тонкие, ровно вырезанные образцы, узкие, с малым поперечным сечением вблизи образца ультразвуковые пучки (что достигается, например, в случае фокусирующих преобразователей), приемники малых размеров, а также прибегая к увеличению расстояния между образцом и приемником. Три последних требования подразумевают, что приемник находится в дальнем поле (зоне Фраунгофера), а сама область фазовых искажений расположена в «дальнем поле» приемника.
Заметим, что различные требования, позволяющие решить рассмотренные выше проблемы, противоречат друг другу. Поэтому при разработке той или иной измерительной системы зачастую приходится применять компромиссные решения.
4.4.2.4. Контрольные измерения на стандартных материалах
С учетом большого числа возможных источников погрешностей при измерении коэффициента затухания, а также из-за трудностей количественной оценки многих из этих погрешностей представляется целесообразным испытывать любую новую измерительную систему методом контрольных измерений на каких-либо стандартных материалах с хорошо известными характеристиками. В случае систем, обеспечивающих проведение абсолютных измерений с высокой точностью, в качестве подобного тест-материала обычно используется чистая вода [181]. Для тех систем, которые предназначены для выполнения относительных измерений на биологических тканях, пока не существует фантомов, которые имитировали бы свойства этих неоднородных тканей в плане искажения акустического пучка и рассеяния. В качестве же однородного тест-материала широко используется касторовое масло. Это вызвано тем, что скорость звука и затухание в касторовом масле близки к соответствующим параметрам многих мягких тканей. На основе анализа имеющихся данных Данн и Бейер [51] получили для касторового масла эмпирическое соотношение, которое справедливо в диапазоне частот 0,5 — 500 МГц.
![]()
где а имеет размерность дБ/см, а частота f выражена в МГц. Зависимость затухания от температуры для этого материала в интервале температур 0 — 40° С можно представить в форме Аррениуса [53]
![]()
где Т выражена в Кельвинах; в более приемлемом для практических расчетов виде эта зависимость имеет следующую форму:
![]()
где Т выражена в градусах Цельсия.
В качестве тест-материала можно также использовать хлопковое масло, для которого а = 0,035/2 (дБ/см) при температуре 26 °С [51]. Однако следует учитывать, что из-за более низкого затухания в этом материале к точности измерительной системы предъявляются более жесткие требования. Кроме того, хлопковое масло не столь доступно, как касторовое.
4.4.2.5. Влияние условий измерений
Как было ранее показано, для обеспечения достаточной точности измерений коэффициента затухания ультразвука обычно приходится работать на образцах удаленной ткани и лишь в редких случаях оказываются возможны измерения in vivo. Аналогичная ситуация возникает и при измерениях скорости или рассеяния звука. Основная проблема заключается в том, каким образом следует обработать образцы биологических тканей, чтобы по возможности облегчить проведение измерений и в то же время не исказить характеристики живых тканей и гарантировать, что результаты совпадут с результатами измерений, выполненных через какой-то период времени и, возможно, на другой аппаратуре и других образцах. Как показано в табл. 4.3, все эти проблемы можно разбить на две основные группы вопросов, которые мы теперь и рассмотрим.
До последнего времени существовало лишь несколько работ, результаты которых можно было бы использовать для получения ответов на поставленные вопросы, а в целом наши знания в этой области еще очень скудны. Как отмечает Бэмбер [8], требуется очень продуманно подходить к вопросам подготовки образцов биологических тканей к измерениям, выбора образцов и конфигурации измерительной схемы, а также контроля за условиями измерений. Отсутствие специальных мер предосторожности будет приводить к большому расхождению значений а, измеренных как на одном образце, так и на разных образцах. Это, в частности, справедливо для образцов печени и жировой ткани, разброс результатов измерения на которых может достигать нескольких сотен процентов на фиксированной частоте. Большое расхождение данных, опубликованных в литературе для того ли иного органа, может объясняться влиянием какого-либо одного или всех факторов, перечисленных в группе А табл. 4.3 [87].
Таблица 4.3
А. Старение образцов. На взятых из ряда органов образцах, хранившихся при комнатной температуре, показано [12], что процессы автолиза, идущие в образцах тканей по крайней мере пять дней после того, как их вырезали из органа, незначительно влияют на величину затухания ультразвука, если все образующиеся газы удаляют. Временные изменения за счет автолиза (а именно уменьшение коэффициента затухания а со временем, но не более чем на 15% за 30 ч) были малы по сравнению с большим разбросом результатов различных измерений, о которых упоминалось ранее. В то же время Фриззелл и др. [72], а также Бэмбер и др. [12] отмечают заметное влияние газов, выделяющихся при распаде биологических тканей. Влиянию неудаленных газов можно приписать рост а в тканях селезенки коровы [39] и миокарда собаки [169], который наблюдался с течением времени после их вырезания. В миокарде собаки спустя 4 ч после смерти животного затухание возрастало в среднем на 20%, если образцы ткани хранились при температуре 35°С. Если же температура хранения была равна 19,5°С, то каких-либо существенных изменений затухания не отмечалось. Сообщалось, что при температуре хранения 4°С старение образца ткани человеческого мозга вызывало уменьшение коэффициента затухания а приблизительно на 21% при повторении измерений через день после вырезания образца [118]. В течение последующих четырех дней этот параметр больше не изменялся. Согласно работе [12], затухание ультразвука в ткани мозга коровы через два дня после приготовления образца уменьшалось всего на 8%. При этом температура хранения составляла 20°С.
На образцах тканей человеческого мозга [118] и миокарда коровы [193] было показано, что старение образцов влияет на скорость звука весьма незначительно. За 5 — 6 дней наблюдалось относительное уменьшение скорости звука всего на 1%. В отличие от скорости звука сечение обратного рассеяния с течением времени, прошедшего после смерти, может существенно уменьшаться, если образцы хранятся при температуре 20°С [12]. Однако при температуре хранения 4°С в образцах ткани миокарда коровы этот параметр практически не менялся в течение шести дней [193].
Б. Влияние газовых пузырьков. Вклад газовых пузырьков в коэффициент затухания печени рассчитывался для различных частот на основе уравнения (4.32) [15]. Под действием этого механизма затухания в образцах, наполненных газом, должно отмечаться избыточное затухание звука, причем в области низких частот коэффициент затухания а почти не должен зависеть от частоты. Из анализа опубликованных данных следует, что эти теоретические предсказания выполняются и что результаты измерений хорошо согласуются друг с другом независимо от метода измерений. Следует отметить, что методы местной откачки и ручной пальпации, которые часто упоминаются в литературе, позволяют в лучшем случае лишь частично удалить из образцов имеющийся в них газ. Охлаждение ткани может оказаться в этом плане более эффективным [15, 72], поскольку при понижении температуры возрастает растворимость газов в воде и после повторного повышения температуры образцов исследователь будет располагать определенным временем для проведения измерений до того момента, когда газы вновь начнут выделяться из раствора. Аналогичная идея лежит в основе и другого метода, заключающегося в повышении статического давления в окружающей образец среде. Фриззелл [72] и Паркер [175] с успехом применили этот метод, причем Фриззелл выдерживал исследуемые образцы под давлением 33 бар (3 • 10-6 Па) в течение 90 мин, а Паркер воздействовал давлением 27 бар в течение 30 мин и помещал образцы в герметически закрытый полиэтиленовый контейнер, чтобы предотвратить возможность растворения газов, находящихся под избыточным давлением.
Следует отметить, что для некоторых тканей проблема, связанная с образованием газов, может быть не столь серьезной, как для печени [12]. Тем не менее при подготовке свежевырезанных образцов к измерениям всегда необходимо учитывать возможный вклад газовых пузырьков.
В. Условия консервации. По всей видимости, среда, в которой хранятся образцы биологических тканей и проводятся измерения, влияет на результаты измерений. Фриззелл и др. [72] обнаружили, что пои хранении образцов печени и проведении измерений в воде эти образцы неизменно характеризовались более низкими значениями коэффициентов затухания по сравнению с образцами, хранящимися и исследуемыми в физиологическом растворе. Это различие составляло 6— 12%, хотя не исключено, что при использовании физиологического раствора в исследуемых образцах содержалось большее количество газов.
Г. Замораживание образцов. Важно знать, будут ли акустические свойства биологических тканей сохраняться при их замораживании. Кросби и Маккэй [39] зафиксировали существенное возрастание коэффициента затухания мягких тканей непосредственно в процессе их замораживания. Майлз и Каттинг [148] нашли, что в случае мышечной ткани коровы между скоростью звука и относительным содержанием незамерзшей воды в образцах существует тесная взаимосвязь. Фриз и Макоу [70] показали, что коэффициенты затухания и сечения обратного рассеяния в тканях млекопитающих (коровы) и рыб в свежевырезанных образцах тканей и образцах, которых подвергались заморозке с последующим размораживанием, значительно различаются. Рост затухания и обратного рассеяния после размораживания связывался с влиянием небольших полостей, образуемых кристаллами льда и растворенным воздухом, выделившимся из раствора в процессе замораживания. Это полностью согласуется с данными Фриззелла и др. [72] для печени. Эти авторы также показали, что дегазация размороженных образцов приводит к снижению коэффициента затухания до значений, близких к измеренным с помощью термоэлектрического метода нестационарного нагрева. В свою очередь результаты термоэлектрических измерений практически совпадали с результатами измерений на образцах свежевырезанной ткани. В работе [68], однако, отмечается, что на одном из образцов ткани молочной железы процесс замораживания — оттаивания приводил к некоторому уменьшению (на 4%) коэффициента затухания. При этом изменений скорости звука не обнаружено.
Д. Фиксация образцов. Химическая фиксация широко применялась в течение многих лет для сохранения свойств образцов биологических тканей в процессе их гистологического и анатомического исследования. Для этих целей использовались самые различные химические соединения, причем наиболее распространенное из них — формалин — применялся многими исследователями и для консервации образцов, предназначенных для акустических измерений. И только недавно анализ влияния фиксации образцов на их акустические характеристики стал предметом специальных исследований. Большая часть известных фактических данных по этому вопросу собрана в работе Бэмбера и др. [13], посвященной изучению действия различных фиксирующих веществ. Было отмечено существенное различие в действии того или иного фиксирующего раствора на биологическую ткань. В частности, оказалось, что фиксация в формалине действительно позволяет в определенной мере сохранить акустические характеристики некоторых тканей, однако в целом наблюдались заметные изменения, вызванные процессом фиксации. Эти изменения сводились к следующему. Во-первых, наблюдался рост коэффициента затухания в среднем на 10% на частоте 1 МГц и на 50% на частоте 7 МГц. Во-вторых, скорость звука уменьшалась в среднем примерно на 1,5% и, в-третьих, коэффициент обратного рассеяния спадал в среднем на 15% на частоте 1 МГц и на 45% на частоте 4 МГц. Эти результаты в отношении затухания и скорости звука согласуются с более свежими данными измерений на человеческом мозге [118]. В целом после фиксации в формалине образцы тканей характеризовались меньшими пространственными вариациями по сравнению с образцами свежеудаленных тканей. Повышение жесткости за счет фиксации обеспечивало возможность изготовления образцов с более равномерной толщиной. Как показали результаты измерений, выполненных Бэмбером и Хиллом [10], в интервале температур от 5 до 40 °С температурные зависимости коэффициента затухания а для свежевырезанных и фиксированных тканей имели аналогичный характер. С другой стороны, заметные изменения акустических характеристик после фиксации в формалине отмечались у тканей с анизотропными свойствами. В частности, фиксация вызывала возрастание а на 30% в скелетных мышцах коровы при измерении затухания акустической волны, распространяющейся перпендикулярно мышечным волокнам. Если же волокна были ориентированы параллельно направлению распространения звука, фиксация не приводила к каким-либо заметным изменениям затухания [163].
Е. Влияние температуры и давления. Влияние температуры и давления на надежность и точность измерений затухания звука рассматривалось в разд. 4.4.2.2. Вообще говоря, небольшие изменения температуры не влекут за собой каких-либо серьезных проблем, однако следует отметить, что расхождения опубликованных данных по акустическим свойствам конкретных тканей (в частности, жировой ткани) в определенной степени могут объясняться существенным различием тех температур, при которых проводились измерения [10].
Ж. Изменчивость, присущая биологическим тканям. Немного существует работ, в которых исследуются статистические вариации акустических параметров различных органов и тканей, «нормальных» во всех отношениях. Эти вариации возникают в зависимости от биологического вида, пола, расы, продолжительности жизни и т. д. Известно, например, что с возрастом изменяется содержание коллагена в сердце и печени [61], а также содержание воды в мозге [4]. Последнее является, по-видимому, причиной того, что затухание звука в мозге ребенка примерно в три раза меньше затухания в мозге взрослого человека [118]. Установлено также, что скорость звука в молочной железе уменьшается с возрастом (см. разд. 5.3.3). Не исключено, что вариации акустических параметров будут наблюдаться у образцов, извлеченных из различных участков идентичных тканей или органов, или ориентированных различным образом. В то же время измерения на печени и сухожилиях [90] показывают, что, по всей видимости, коэффициент поглощения звука, по крайней мере для указанных тканей, слабо зависит от биологического вида.
3. Изменения после смерти. Рассмотренные выше проблемы весьма далеки от полного решения, однако еще меньше мы можем сказать в ответ на второй важный вопрос из табл. 4.3, касающийся взаимосвязи акустических параметров тканей в прижизненном состоянии и после смерти. Из-за почти полного отсутствия информации вопросы, указанные в группе Б табл. 4.3, являются весьма дискуссионными и нуждаются в уточнении по мере появления новых фактических данных. По ряду причин прекращение кровотока может сделать исследуемую ткань непригодной для определенных измерений [136], хотя в работах [45, 187] не было найдено каких-либо существенных различий в скорости звука и затухании между живой тканью и тканью после смерти. В работе [98] было высказано предположение, что различие в кровеносных системах серого и белого вещества мозга, а также пульсации живого мозга увеличивают рассогласование акустических импедансов этих тканей. В результате границы между серым и белым веществом живого мозга становятся более заметными на акустическом эхо-импульсном изображении по сравнению со случаем удаленного мозга, хотя последний фиксировался в формалине. Можно предположить, что наблюдаемые различия между живыми и удаленными тканями в значительной мере будут объясняться температурной зависимостью акустических параметров [10, 79, 118], если измерения in vitro не проводятся при естественной температуре тела. Однако в работе [208] было обнаружено, что коэффициент затухания на частоте 0,97 МГц в мозге собаки возрастал на 7 — 25°7о после ее внезапной смерти. Очевидно, что такое изменение затухания нельзя объяснить только на основе температурных различий. С другой стороны, авторы работы [149] показали, что значения скорости звука в конечностях живых животных (эти конечности почти целиком состоят из подкожного жира и мышечной ткани) лежат между значениями скорости звука, измеренными при температуре тела в удаленных образцах жировой и мышечной ткани. В работе [72] с помощью термоэлектрического метода нестационарного нагрева проводились сравнительные измерения коэффициента поглощения звука в печени мыши in vivo и непосредственно после смерти животных. Статистическая обработка полученных результатов показала, что никаких заметных различий в обоих случаях нет. В работе [137] измерялось уменьшение коэффициента затухания в мышечной ткани кошки в течение 4 ч после смерти животного. При этом температура поддерживалась на уровне 38 °С. За указанное время коэффициент затухания на частоте 1,75 МГц уменьшился в среднем на 24%. Для сравнения следует отметить, что исходные вариации коэффициента затухания между пятью различными животными составляли ±53%. Было также обнаружено, что после 4-часового периода затухание вновь начинало возрастать.
4.5. Обзор литературных данных о коэффициентах затухания и поглощения
Анализу акустических характеристик биологических тканей посвящены прекрасные обзорные работы Карстенсена [30], Данна и др. [53], Данна и О'Брайена [56], Джонстона и др. [107], Уэллса [203]. По опубликованным данным составили сводные таблицы акустических параметров различных органов и тканей Чиверс и Парри [35], Голдман и Хьютер [81], Госс и др. [87, 88]. Мы не будем здесь подробно воспроизводить имеющийся обширный материал, хотя на нем и строится весь настоящий раздел. Основное внимание мы уделим тем вопросам, которые не рассматривались или были неправильно истолкованы в оригинальных обзорах. Кроме того, мы остановимся на новых данных, которые были получены за последнее время. Частично эти данные уже приводились в разд. 4.4.2.5. При знакомстве с настоящей главой для удобства сравнения результатов мы рекомендуем читателю обращаться к рис. 4.10.
4.5.1. БИОЛОГИЧЕСКИ «ПРОСТЫЕ» СРЕДЫ
По-видимому, Хьютер [104] был первым, кто указал на существование взаимосвязи между коэффициентом затухания звука и сложностью структуры биологических сред. К «простым» по своей структуре средам можно отнести воду и биологические молекулы в водном растворе или суспензии. Исследование водных растворов макромолекул шло достаточно интенсивно.
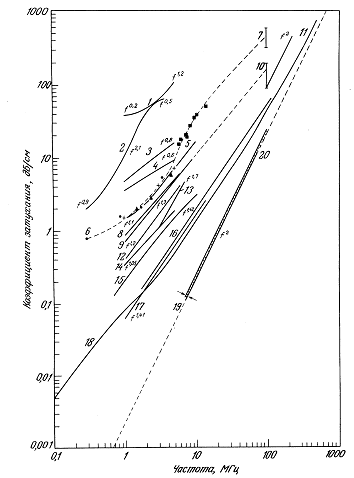
Рис. 4.10. Зависимости коэффициентов затухания звука от частоты в различных тканях и биологических жидкостях. Для большинства мягких тканей опубликованные данные характеризуются большим разбросом, причем полученные значения перекрываются для тканей различного вида. Для костных тканей также получен широкий диапазон значений коэффициента затухания (здесь не приводится). Представленные примеры были выбраны лишь для демонстрации характерных частотных зависимостей и соотношений между параметрами тканей. ![]() — Легкие [46]; 2 — кости черепа [103]; 3 — сухожилия (данные Дуссика и Фритча, взятые из работы [87]; 4 — кожа (данные Дуссика и Фритча, взятые из работы [87]); 5 — молочная железа (усредненные значения) [9]; 6 — скелетная мышца при распространении звука параллельно волокнам (данные Коломбати и Петральи, Дуссика и др., Бушмана и др. и Хьютера, взятые из работы [35]); 7 — фиксированная сердечная мышца на частоте 100 МГц [209]; 8 — мозг взрослого человека [8, 118]; 9 — печень на частотах 1 — 10 МГц [177]; 10 — печень на частоте 100 МГц [197, 183]; 11 — почка на частотах 100 и 220 МГц [ПО]; 12 — селезенка [8]; 13 — семенники [8]; 14 — мозг ребенка [118]; 75 — цельная кровь [32]; 16—кистозная жидкость молочной железы [126] (9,4%-ный белковый раствор); 77—плазма крови [32]; 18— 10%-ный раствор гемоглобина при температуре 25 °С [119, 204]; 19 — диапазон значений для растворов аминокислот [119]; 20 — вода [181].
— Легкие [46]; 2 — кости черепа [103]; 3 — сухожилия (данные Дуссика и Фритча, взятые из работы [87]; 4 — кожа (данные Дуссика и Фритча, взятые из работы [87]); 5 — молочная железа (усредненные значения) [9]; 6 — скелетная мышца при распространении звука параллельно волокнам (данные Коломбати и Петральи, Дуссика и др., Бушмана и др. и Хьютера, взятые из работы [35]); 7 — фиксированная сердечная мышца на частоте 100 МГц [209]; 8 — мозг взрослого человека [8, 118]; 9 — печень на частотах 1 — 10 МГц [177]; 10 — печень на частоте 100 МГц [197, 183]; 11 — почка на частотах 100 и 220 МГц [ПО]; 12 — селезенка [8]; 13 — семенники [8]; 14 — мозг ребенка [118]; 75 — цельная кровь [32]; 16—кистозная жидкость молочной железы [126] (9,4%-ный белковый раствор); 77—плазма крови [32]; 18— 10%-ный раствор гемоглобина при температуре 25 °С [119, 204]; 19 — диапазон значений для растворов аминокислот [119]; 20 — вода [181].
Интерес к этим средам объяснялся предполагаемой ведущей ролью механизмов молекулярной релаксации в затухании ультразвука в биологических тканях. В частности, Паули и Шван [177] на основе измерений затухания звука в цельной печени и ее гомогенате, состоящем из субклеточных компонентов печени, убедительно доказали, что основной вклад в затухание вносит поглощение на макромолекулярном уровне.
Некоторые свойства воды обсуждались в разделе 4.3.5, где рассматривалась модель структурной релаксации молекул воды с двумя устойчивыми состояниями. Такая модель была предложена Холлом [53, 92]. Процесс перестройки из одного состояния в другое характеризуется, по-видимому, постоянной времени, равной приблизительно 10-12 с. В результате поглощение на частоте около 1 МГц оказывается пропорциональным f2, однако значение ![]() (равное 15,7-10-17 с2/см при температуре 37 °С) превышает расчетное значение этого параметра, полученное с учетом только классических механизмов.
(равное 15,7-10-17 с2/см при температуре 37 °С) превышает расчетное значение этого параметра, полученное с учетом только классических механизмов.
4.5.1.1. Внутримолекулярное поглощение
На частотах, используемых в медицинской практике, поглощение ультразвука водой, находящейся в тканях, вносит пренебрежимо малый вклад в суммарное затухание. Рассматривая компоненты тканей в порядке возрастания сложности их структуры, можно видеть, что первый заметный вклад в величину поглощения вносят биополимеры. Мономеры, такие, например, как аминокислоты, в водном растворе интересны тем, что при соответствующих значениях рН они обусловливают поглощение, которое можно описывать процессом с одной частотой релаксации. Однако поглощение в растворе биополимера значительно больше поглощения в соответствующем растворе мономеров, из которых составлен данный полимер. Подобная закономерность, которую можно охарактеризовать как «целое много больше суммы частей», справедлива для биополимеров разной природы: белков, нуклеиновых кислот и полисахаридов.
На самом деле ситуация еще более сложна. Коэффициент удельного поглощения любого конкретного биополимера растет с увеличением молекулярной массы только в пределах интервала значений молекулярной массы, не превышающих массу 100 мономеров [121]. По обеим сторонам этого интервала коэффициент удельного поглощения никак не коррелирует с молекулярной массой (т. е. в пределах таких групп, как аминокислоты или белки). Непонятно, какие свойства молекул ответственны за различия в поглощении в пределах этих групп. По-видимому, конформационные перестройки молекул определяют некоторые из этих свойств, но в какой степени — неизвестно. Желатин, который является денатурированной формой коллагена и в водных растворах имеет структуру случайного клубка, характеризуется значительно меньшим удельным поглощением по сравнению с глобулярными белками, обладающими третичной и четвертичной структурами. Нативный коллаген и ДНК (дезокси-рибонуклеиновая кислота) в водных суспензиях или растворах характеризуются еще более высоким по сравнению с белками удельным поглощением. Обе эти молекулы имеют очень высокий уровень структурной организации (тройная спираль и, соответственно, двойная спираль). С другой стороны, величины удельного поглощения молекул полисахаридного декстрана и фиколла, имеющих одинаковый молекулярный вес, приблизительно совпадают, хотя молекулы декстрана представляют собой длинные цепочки, а молекулы фиколла имеют глобулярную структуру. Вклады в поглощение, обусловленные классическими вязкими потерями, для этих молекул совершенно различны. В общем случае сдвиговая вязкость растворов макромолекул никак не коррелирует с коэффициентом поглощения звука.
Частотные зависимости поглощения ультразвука аналогичны для всех полимеров, обладающих структурной организацией высокого порядка. Этот факт наводит на мысль, что поглощение в таких полимерах обусловлено действием одного и того же механизма, отличного, к примеру, от механизма поглощения в желатине. Близкая к линейной форма частотной зависимости поглощения в этих полимерах свидетельствует о распределении времен релаксации, однако конкретные механизмы действующих релаксационных процессов неизвестны. Общепринятым является мнение, что при нормальных физиологических значениях рН наиболее существенный вклад в поглощение обусловлен, вероятно, возмущениями гидрат-ных оболочек макромолекул под действием ультразвука. Перераспределение этих областей высокоструктурированной воды, окружающей каждую молекулу, приводит к поглощению энергии в процессе структурной релаксации. Возможно, что поглощение ультразвука определяется конформацией биополимера в той степени, в какой она влияет на равновесие между связанными и свободными молекулами. Такие механизмы часто называют взаимодействиями между растворенным веществом и растворителем. Гипотеза о структурной релаксации в определенной степени подтверждается результатами работы [195], авторы которой зафиксировали наличие небольших отрицательных температурных коэффициентов поглощения.
Несмотря на то, что липиды в той или иной форме составляют вторую основную компоненту сухого веса многих мягких тканей (первую образуют белки), исследованию их акустических характеристик уделялось сравнительно мало внимания. В тех работах, которые были посвящены этому вопросу, рассматривались липиды и структуры, связанные с клеточными мембранами, и использовались суспензии фосфолипидов типа лецитина в форме биослоев, образующих липосомы. При таких условиях поглощение звука может быть рассмотрено в рамках либо одиночного релаксационного процесса [78], либо нескольких действующих релаксационных процессов [94] с частотами релаксации, лежащими в диапазоне от 1,6 до 16 МГц. Возможно, что механизмы этих процессов заключаются в конформационных перестройках, связанных с переходом из кристаллической в жидкокристаллическую фазу. Такой фазовый переход происходит при температуре около 41,3 °С, когда амплитуда релаксации максимальна и скорость звука достигает локального минимума, характеризующегося очень большим отрицательным значением температурного коэффициента [146, 151]. По-видимому, на частотах выше 150 МГц какие-либо дополнительные релаксационные процессы с существенной амплитудой не действуют.
4.5.1.2. Межмолекулярное поглощение
При малых концентрациях макромолекул в растворе часто, хотя и не всегда, зависимость поглощения от концентрации на начальном участке оказывается линейной, т. е. удельное поглощение имеет постоянное значение. Именно на этом участке основную роль играют рассмотренные выше механизмы внутримолекулярного поглощения. При достаточно высоких концентрациях в растворе удельное поглощение возрастает с ростом концентрации макромолекул. Как считают, это явление обусловлено усилением влияния некоторого, пока еще не изученного, механизма взаимодействия между самими макромолекулами. Высказывалось предположение, что при уровнях концентрации, соответствующих концентрации молекул в интактных биологических тканях, основной вклад в поглощение звука тканями вносят механизмы межмолекулярного поглощения (solute — solute interactions).
Имеются и другие факты, свидетельствующие в поддержку идеи о том, что взаимодействия между макромолекулами играют важную роль. Кремкау и Карстенсен [119, 120] собрали все соответствующие данные, полученные к тому времени, причем некоторые из них касались обработки растворов макромолекул специальными химическими препаратами, усиливающими молекулярные взаимодействия. Один из классов таких препаратов образуют гистологически фиксирующие вещества, которые способствуют образованию сшивок между соседними белковыми молекулами. Обработка такими веществами приводит к повышению жесткости и сохранности биологических тканей. Влияние фиксирования в формалине на акустические характеристики неповрежденных тканей, о котором шла речь в разд. 4.4.2.5, можно теперь рассматривать как эффект, подтверждающий в определенной мере предположения Кремкау и Карстенсена. Оказалось, что усиление связей между белковыми молекулами приводит к увеличению поглощения, но по неясным причинам оно вызывает также уменьшение скорости звука. В этом плане представляет интерес скелетная мышца, поскольку сокращение мышечных волокон связано с ростом коэффициента затухания [22, 80] и при некоторых обстоятельствах с небольшим уменьшением скорости звука (см. разд. 5.3.1). Хотя конкретный действующий механизм этих явлений не установлен, по-видимому, можно провести аналогии между образованием актин-миозиновых поперечных мостиков при мышечном сокращении и действием полимеризую-щих фиксирующих препаратов [7].
Как всегда, существуют данные, нарушающие ясность картины и запутывающие ситуацию. Можно отметить, например, что денатурация и дегидратация белков биологических тканей под влиянием этилового спирта [13], нагрева или изменения рН [131, 177] приводят к повышению затухания и поглощения звука.
4.5.2.1. Влияние метода измерений
Между данными о коэффициентах поглощения и затухания звука в биологических тканях, опубликованными разными авторами, существуют значительные расхождения. Это наблюдается даже в тех случаях, когда предположительно речь идет об одних и тех же органах животных одного вида. Все это затрудняет возможность обобщения имеющихся данных с целью проверки предложенных теоретических гипотез или разработки надежных рекомендаций по созданию ультразвуковой аппаратуры. Необходимо весьма осторожно подходить к анализу и интерпретации имеющихся экспериментальных данных.
В разд. 4.4.2.5 уже отмечалось, что очень часто причиной расхождения полученных результатов является различие в условиях измерений. Кроме того, эти расхождения могут быть связаны с существованием и применением большого разнообразия методов измерений (разд. 4.4.1). По-видимому, наиболее заметное различие возникает между так называемыми фазочувствительными системами и системами, регистрирующими энергию сигнала (не чувствительными к фазе), при их использовании для измерений параметров одних и тех же образцов биологических тканей. Полхаммер и др. [183] на примере печени коровы показали, что при использовании различных, но не чувствительных к фазе методов измерений можно получить воспроизводимые результаты для коэффициентов затухания в широком диапазоне частот — от 1 до 100 МГц. Тем не менее, на основе данных, опубликованных для мягких тканей, в общем случае очень непросто провести различие между истинными изменениями биологического характера и вариациями, обусловленными систематическими погрешностями. Поэтому при анализе зависимостей акустических параметров от каких-либо других свойств ткани или внешних условий (например, температуры) желательно ограничиться (хотя это часто и невозможно) рассмотрением данных, полученных в какой-либо одной лаборатории, где указанные зависимости исследовались специально.
4.5.2.2. Вклад рассеяния в затухание звука
Оценка вклада, который рассеяние вносит в суммарное затухание в исследуемой ткани, является, по-видимому, первым существенным шагом к пониманию механизмов рассеяния и поглощения акустических волн в тканях. Удивительно, что для большинства биологических тканей отношение либо не известно, ![]() либо его измеренное значение является весьма спорным. Во многом это связано с трудностями сравнения опубликованных данных, полученных в разных лабораториях, а также со сложностью проведения прямых измерений величины
либо его измеренное значение является весьма спорным. Во многом это связано с трудностями сравнения опубликованных данных, полученных в разных лабораториях, а также со сложностью проведения прямых измерений величины ![]() (см. гл. 6). Следует также напомнить, что результаты измерений коэффициента затухания могут зависеть от конкретной геометрии измерительной схемы (см. разд. 4.2 и 4.4.2.1).
(см. гл. 6). Следует также напомнить, что результаты измерений коэффициента затухания могут зависеть от конкретной геометрии измерительной схемы (см. разд. 4.2 и 4.4.2.1).
Для некоторых биологических сред анализ и оценка реальных значений ![]() не вызывает больших затруднений. Во-первых, в человеческом организме существует ряд однородных биологических сред, в которых при отсутствии патологических изменений рассеяния звука, по-видимому, вообще не происходит, по крайней мере на тех частотах, которые обычно используются в медицинской практике. Примерами таких сред могут служить околоплодная жидкость, влага передней камеры, стекловидное тело, хрусталик глаза и кистозная жидкость.
не вызывает больших затруднений. Во-первых, в человеческом организме существует ряд однородных биологических сред, в которых при отсутствии патологических изменений рассеяния звука, по-видимому, вообще не происходит, по крайней мере на тех частотах, которые обычно используются в медицинской практике. Примерами таких сред могут служить околоплодная жидкость, влага передней камеры, стекловидное тело, хрусталик глаза и кистозная жидкость.
Во-вторых, не вызывает сомнения тот факт, что наличие границ раздела между воздухом и тканью в легких приводит к очень большому затуханию ультразвука в этом органе. Уравнения, описывающие затухание на газовых пузырьках (разд. 4.3.3), использовались Данном и Фраем [52] для теоретических оценок величины и частотной зависимости затухания в легких. Следует, однако, отметить, что предсказанный минимум затухания в частотной области 4 — 7 МГц в дальнейшем не получил экспериментального подтверждения [46]. Вместо этого было показано, что затухание в легких монотонно возрастает с ростом частоты в диапазоне от 1 до 6 МГц.
В-третьих, нет расхождения в мнениях относительно того, что присутствие интактных клеток в крови определяет лишь незначительную долю затухания, большая часть которой в основном обусловлена вязкими потерями за счет относительного движения (см. следующий раздел). Ниже мы приведем результаты прямого измерения абсолютных значений ![]() для крови. В работе [194] была получена интересная зависимость
для крови. В работе [194] была получена интересная зависимость ![]() от изменения показателя гема-токрита с максимумом при концентрации красных кровяных телец, равной 26%, т.е. при концентрации более низкой, чем в нормальной крови.
от изменения показателя гема-токрита с максимумом при концентрации красных кровяных телец, равной 26%, т.е. при концентрации более низкой, чем в нормальной крови.
Все возможные способы определения вкладов поглощения и рассеяния в затухание звука можно разделить на прямые и косвенные методы. Прямые методы измерения коэффициента поглощения были рассмотрены в разд. 4.4.1.1; лишь совсем недавно были предприняты попытки прямых измерений коэффициента рассеяния, не требующие данных о коэффициентах поглощения или затухания звука. При измерениях абсолютных значений сечения рассеяния единичного объема возникает ряд серьезных проблем, связанных с необходимостью точных оценок поправочных коэффициентов. Введение таких поправочных коэффициентов требуется для того, чтобы сделать результаты измерений не зависящими от конкретного типа той аппаратуры, которая используется как для получения абсолютного значения дифференциального сечения рассеяния единичного объема при выбранном угле рассеяния (для этой цели часто используется обратное рассеяние), так и для определения с высокой точностью усредненного углового распределения рассеяния. На это угловое распределение существенно влияют форма образца и вариации угла перекрытия характеристик направленности приемника и излучателя. Несмотря на все эти трудности, результаты прямого измерения рассеяния позволяют, по-видимому, получить наиболее точные на сегодняшний день оценки отношения Кэмпбелл и Вааг [28] нашли, что для печени теленка отношение ![]() составляет примерно 2% в частотном диапазоне 3 — 7 МГц. Нассири и Хилл [161] для частотного диапазона 4 — 7 МГц получили приближенные значения этого отношения для печени человека, мышечной ткани и крови. Они равнялись соответственно 19, 17 и 0,3%. Полученные данные представляют большой интерес, поскольку с их помощью можно одновременно контролировать значения
составляет примерно 2% в частотном диапазоне 3 — 7 МГц. Нассири и Хилл [161] для частотного диапазона 4 — 7 МГц получили приближенные значения этого отношения для печени человека, мышечной ткани и крови. Они равнялись соответственно 19, 17 и 0,3%. Полученные данные представляют большой интерес, поскольку с их помощью можно одновременно контролировать значения ![]() и
и ![]() , найденные в результате прямых измерений. Паркер [175] провел прямые измерения
, найденные в результате прямых измерений. Паркер [175] провел прямые измерения ![]() и
и ![]() в образцах печени коровы и на основе сравнения дисперсии двух наборов данных установил, что на частотах 1,1 и 3,3 МГц значения этих величин статистически неразличимы. Заметное различие, соответствующее значению
в образцах печени коровы и на основе сравнения дисперсии двух наборов данных установил, что на частотах 1,1 и 3,3 МГц значения этих величин статистически неразличимы. Заметное различие, соответствующее значению ![]() = 18%, наблюдалось лишь на частоте 5,6 МГц.
= 18%, наблюдалось лишь на частоте 5,6 МГц.
Помимо прямых методов измерения существует большое число косвенных методов оценки вкладов поглощения и рассеяния в затухание звука, однако эти методы, как правило, позволяют получить лишь вспомогательные данные. Наиболее убедительной в этом плане представляется классическая работа Паули и Швана [177], в которой показано, что затухание звука в цельной печени коровы уменьшается после гомогенизации ткани. Из полученных ими результатов следует [101], что в частотном диапазоне 1 — 10 МГц значение ![]() для печени составляет приблизительно 30%. В этом исследовании предполагалось, что процесс гомогенизации, который приводит к устранению из ткани всех рассеивающих структур вплоть до структур субклеточного уровня, не влияет на коэффициент поглощения звука. Справедливость такого предположения вызывает большие сомнения, поскольку определенный вклад в поглощение могут давать потери, возникающие на неоднородностях ткани за счет вязкого относительного движения. Тем не менее полученное значение 30% представляет полезную информацию, поскольку оно определяет верхний предел возможных значений
для печени составляет приблизительно 30%. В этом исследовании предполагалось, что процесс гомогенизации, который приводит к устранению из ткани всех рассеивающих структур вплоть до структур субклеточного уровня, не влияет на коэффициент поглощения звука. Справедливость такого предположения вызывает большие сомнения, поскольку определенный вклад в поглощение могут давать потери, возникающие на неоднородностях ткани за счет вязкого относительного движения. Тем не менее полученное значение 30% представляет полезную информацию, поскольку оно определяет верхний предел возможных значений ![]() в печени, с которым можно сравнивать результаты других оценок.
в печени, с которым можно сравнивать результаты других оценок.
Предпринимались попытки сравнительного анализа опубликованных данных по результатам измерений величин ![]() и д. Следует отметить, однако, что даже в случае использования фазонечувствительной аппаратуры для измерения затухания есть опасность, что на результаты измерения затухания звука сильно влияет наличие в среде газовых пузырьков (а также ряд других факторов), тогда как на результатах измерения поглощения все это никак не сказывается. Госс и др. [90], а также Полхаммер и др. [183] получили, что в частотном диапазоне 0,5 — 10 МГц значения для печени лежат в интервале 23 — 61%. В некоторых работах приводятся и более низкие значения этого отношения.
и д. Следует отметить, однако, что даже в случае использования фазонечувствительной аппаратуры для измерения затухания есть опасность, что на результаты измерения затухания звука сильно влияет наличие в среде газовых пузырьков (а также ряд других факторов), тогда как на результатах измерения поглощения все это никак не сказывается. Госс и др. [90], а также Полхаммер и др. [183] получили, что в частотном диапазоне 0,5 — 10 МГц значения для печени лежат в интервале 23 — 61%. В некоторых работах приводятся и более низкие значения этого отношения.
Другие методы косвенных оценок основаны на моделировании частотной зависимости затухания в печени с помощью уравнения (4.37), выведенного в разд. 4.3.4 применительно к твердым телам [160], и на анализе различий между поглощением, обратным рассеянием и затуханием звука в процессе распада ткани и ее гистохимической фиксации [7]. В работе [160] в предположении, что коэффициент ![]() пропорционален f4, проводились оценки таких значений множителя В из уравнения (4.37), при которых расчетная частотная зависимость
пропорционален f4, проводились оценки таких значений множителя В из уравнения (4.37), при которых расчетная частотная зависимость ![]() в печени согласовывалась бы с имеющимися экспериментальными данными. Было получено, что в частотном диапазоне 1 — 5 МГц отношение
в печени согласовывалась бы с имеющимися экспериментальными данными. Было получено, что в частотном диапазоне 1 — 5 МГц отношение ![]() составляет приблизительно 1% для нормальной печени и достигает 8— 13% для печени с ожирением. В работе [7] при проведении расчетов предполагалось, что коэффициент поглощения и угловое распределение рассеяния существенно не меняются в процессе распада ткани. В работе [131] наблюдались изменения коэффициента поглощения, вызванные фиксацией в формалине. В этом случае значения параметра
составляет приблизительно 1% для нормальной печени и достигает 8— 13% для печени с ожирением. В работе [7] при проведении расчетов предполагалось, что коэффициент поглощения и угловое распределение рассеяния существенно не меняются в процессе распада ткани. В работе [131] наблюдались изменения коэффициента поглощения, вызванные фиксацией в формалине. В этом случае значения параметра ![]() , полученные для печени, изменялись от 9 до 16% на частоте 4 МГц.
, полученные для печени, изменялись от 9 до 16% на частоте 4 МГц.
По имеющимся данным коэффициент затухания звука в костной ткани может в 2 — 20 раз превышать его значения в мягких тканях, причем опубликованные данные по частотной зависимости затухания в костях сильно расходятся. Несколько авторов [16, 103] считают, что такая частотная зависимость подчиняется закону, который справедлив в тех случаях, когда затухание звука определяется в основном рассеянием на гранулированных структурах (см. разд. 4.3.4). Однако Фрай [74] предполагал, что характер полученной в работе [103] частотной зависимости можно объяснить действием вязких потерь при относительном движении отдельных участков среды.
4.5.2.3. Вклад структурных неоднородностей в поглощение
В разд. 4.3.3 были рассмотрены возможные механизмы (отличные от рассеяния продольной волны), благодаря которым мелкомасштабные структурные неоднородности могут давать вклад в поглощение энергии акустических волн. Карстенсен и Шван [32] установили, что при нормальном показателе гематокрита в частотном диапазоне 0,7 — 4 МГц около 19% затухания ультразвука в крови не может быть обусловлено только поглощением акустической энергии белками крови и должно быть связано с присутствием интактных клеток. При этом приближенные оценки О'Доннелла и Миллера [166] показывают, что относительный вклад поглощения, обусловленного вязким (и тепловым) взаимодействием между этими клетками и окружающей жидкостью, составляет примерно 10%, а из оставшейся части менее 1% может быть отнесено на счет рассеяния продольных волн.
Рассматривая мышечные миофибриллы и фибриллы коллагена в качестве структурных элементов соответственно сердечной мышцы и кожи, О'Доннелл и Миллер попытались также оценить потери на неоднородностях в этих тканях. Для обоих случаев они получили, что вклад этих потерь в величину затухания достигает приблизительно 60%. Эти данные говорят о том, что при анализе многих мягких тканей таким механизмом потерь пренебрегать нельзя.
В работах [81, 163] показано, что затухание звука в скелетных мышцах при распространении волны параллельно мышечным волокнам в 1,6 раза на частоте 0,3 МГц и в 2 раза на частоте 8 МГц больше, чем при распространении звука поперек волокон. Механизм подобной анизотропии не изучен. Можно лишь отметить, что по данным расчетов, выполненных в работе [2], вязкие потери за счет относительного движения частиц асимметричной формы в суспензиях будут больше в том случае, когда частицы ориентированы по направлению движения в звуковом поле своей «узкой», а не «широкой» частью (анизотропия скорости звука в мышечной ткани подробно рассматривается в разд. 5.3.1).
4.5.2.4. Частотная зависимость
Ранее уже обсуждалась частотная зависимость затухания звука в некоторых мягких тканях и других биологических средах. Было получено, что показатель степени т в выражении
![]()
связан с возможными относительными вкладами различных механизмов затухания. Как видно из рис. 4.10, для большинства мягких тканей и биологических жидкостей человеческого организма значения т близки к единице. Экспериментальные исследования показали, что для некоторых тканей эти значения остаются неизменными в достаточно широком частотном диапазоне вплоть до тех частот, на которых существенную роль начинает играть поглощение в воде. При дальнейшем повышении частоты следует ожидать, что значение т для этих тканей будет возрастать и приближаться к т = 2.
Многие авторы, используя различные теоретические модели поглощения звука, рассмотренные в разд. 4.3.1 —4.3.3, пытались объяснить, почему поглощение за период ![]() для мягких тканей остается приблизительно постоянным в пределах широкой полосы частот. Однако явная нехватка опубликованных в литературе сведений пока не позволяет проанализировать ни одно из этих объяснений с нужной степенью глубины.
для мягких тканей остается приблизительно постоянным в пределах широкой полосы частот. Однако явная нехватка опубликованных в литературе сведений пока не позволяет проанализировать ни одно из этих объяснений с нужной степенью глубины.
Анализ отдельных примеров, опубликованных в литературе для мягких тканей, показывает, что уравнение (4.63) далеко не всегда является наилучшей аппроксимацией реальных зависимостей затухания от частоты. На практике довольно часто величина т уменьшается при понижении частоты (иногда она близка к нулю) и стремится к более высоким значениям с ростом частоты. Хотя такое поведение может объясняться погрешностями измерения, связанными с присутствием в тканях газовых пузырьков, можно назвать ряд примеров, которые достаточно убедительно говорят о том, что подобный характер зависимости затухания от частоты определяется свойствами именно исследуемой ткани. В частности, о наличии такого эффекта в мышечной ткани свидетельствуют даже обобщенные литературные данные (рис. 4.10). Видно, что величина ![]() в данном случае принимает минимальное значение на частоте около 3 МГц. Эти факты наводят на мысль, что помимо прочих областей может существовать область низкочастотной релаксации вблизи частоты 40 кГц [104]. В работах [199, 200] было показано, что характеристические частоты многих релаксирующих элементов мышечной структуры действительно лежат в частотной области, примыкающей к 31 кГц.
в данном случае принимает минимальное значение на частоте около 3 МГц. Эти факты наводят на мысль, что помимо прочих областей может существовать область низкочастотной релаксации вблизи частоты 40 кГц [104]. В работах [199, 200] было показано, что характеристические частоты многих релаксирующих элементов мышечной структуры действительно лежат в частотной области, примыкающей к 31 кГц.
4.5.2.5. Температурная зависимость
В разд. 4.3.5 был дан общий анализ влияния температуры на затухание звука с учетом действующих механизмов поглощения и рассеяния. Отметим, что экспериментальные данные, с которыми можно было бы сравнить результаты этого анализа, чрезвычайно скудны.
Наиболее полно информация о температурных зависимостях затухания в мягких тканях собрана в работе Бэмбера и Хилла [10]. Позднее были опубликованы дополнительные данные, подтверждающие выводы указанных авторов [9, 79]. На частотах более 2 МГц в интервале температур (Т) от 6 до 40 °С затухание является монотонно спадающей функцией температуры, причем температурный коэффициент затухания (![]() ) уменьшается с ростом частоты и температуры. Эта зависимость усложняется на более низких частотах, где поглощение и, возможно, затухание звука несколько возрастают при повышении температуры. Аналогичные результаты были получены для яичного белка, поглощение звука в котором на частотах ниже 4 МГц характеризуется небольшим положительным значением температурного коэффициента поглощения. Выше этой частоты температурный коэффициент становится отрицательным [106]. При температурах, превышающих 40 °С, dp/dT для свежевырезанных образцов ткани становится положительным даже на высоких частотах. Возможно, что такое поведение объясняется тепловой денатурацией макромолекул. Жировая ткань характеризуется наибольшим отрицательным значением температурного коэффициента
) уменьшается с ростом частоты и температуры. Эта зависимость усложняется на более низких частотах, где поглощение и, возможно, затухание звука несколько возрастают при повышении температуры. Аналогичные результаты были получены для яичного белка, поглощение звука в котором на частотах ниже 4 МГц характеризуется небольшим положительным значением температурного коэффициента поглощения. Выше этой частоты температурный коэффициент становится отрицательным [106]. При температурах, превышающих 40 °С, dp/dT для свежевырезанных образцов ткани становится положительным даже на высоких частотах. Возможно, что такое поведение объясняется тепловой денатурацией макромолекул. Жировая ткань характеризуется наибольшим отрицательным значением температурного коэффициента ![]() . В частности, на частоте 3 МГц при переходе от температуры тела к комнатной температуре затухание в жировой ткани возрастает почти на 300%, тогда как в других тканях это приращение составляет около 20%. В сложной структуре молочной железы, состоящей как из жировой, так и нежировой ткани, на фиксированных частотах
. В частности, на частоте 3 МГц при переходе от температуры тела к комнатной температуре затухание в жировой ткани возрастает почти на 300%, тогда как в других тканях это приращение составляет около 20%. В сложной структуре молочной железы, состоящей как из жировой, так и нежировой ткани, на фиксированных частотах ![]() может меняться совершенно непредсказуемо в зависимости от направления распространения акустического пучка. Иногда этот коэффициент становится положительным даже на высоких частотах. В среднем же рассматриваемые акустические характеристики молочной железы коррелируют с данными, полученными для других биологических тканей.
может меняться совершенно непредсказуемо в зависимости от направления распространения акустического пучка. Иногда этот коэффициент становится положительным даже на высоких частотах. В среднем же рассматриваемые акустические характеристики молочной железы коррелируют с данными, полученными для других биологических тканей.
Наблюдаемые температурные зависимости затухания в мягких тканях нельзя объяснить действием какого-либо одного механизма поглощения или рассеяния. По-видимому, различные механизмы будут играть преобладающую роль в зависимости от конкретных значений температуры и частоты в том или ином случае. На частотах выше 3 МГц температурная зависимость затухания в нежировых тканях аналогична температурной зависимости, полученной для плазмы крови [31]. Качественно с этим согласуется величина смещения релаксационных частот при изменении температуры, поскольку на частотах выше 3 МГц угловой коэффициент графика зависимости ln(![]() ) от f действительно принимает небольшие положительные значения (см. разд. 4.3.5). Как уже отмечалось в разд. 4.5.2.4, ниже этой частоты для некоторых мягких тканей зависимость In(
) от f действительно принимает небольшие положительные значения (см. разд. 4.3.5). Как уже отмечалось в разд. 4.5.2.4, ниже этой частоты для некоторых мягких тканей зависимость In(![]() ) от f характеризуется небольшими отрицательными значениями углового коэффициента. Такая картина согласуется также с тем, что температурные коэффициенты поглощения (см. выше) имеют положительные значения.
) от f характеризуется небольшими отрицательными значениями углового коэффициента. Такая картина согласуется также с тем, что температурные коэффициенты поглощения (см. выше) имеют положительные значения.
В большинстве мягких тканей на частотах, превышающих 3 МГц, и при температурах выше 20 ° С затухание звука уменьшается с ростом температуры пропорционально корню квадратному из вязкости. На основании этого результата О'Доннелл и др. [169] пришли к заключению, что важную роль в этом процессе могут играть вязкие потери за счет относительного движения. При температурах ниже 20 °С жировая ткань, а также и другие ткани характеризуются отрицательным температурным коэффициентом затухания ![]() , который спадает с ростом температуры значительно круче, чем корень квадратный из вязкости [7]. На рис. 4.11 представлены суммарные данные по поглощению и затуханию звука в тканях центральной нервной системы мыши, кошки и человека. Эти данные получены in vivo, на свежих образцах in vitro, а также на фиксированных образцах. Конечно, нежелательно на одном графике изображать различные величины, полученные при неидентичных условиях на образцах различного вида, однако ограниченность информации исключает другую возможность.
, который спадает с ростом температуры значительно круче, чем корень квадратный из вязкости [7]. На рис. 4.11 представлены суммарные данные по поглощению и затуханию звука в тканях центральной нервной системы мыши, кошки и человека. Эти данные получены in vivo, на свежих образцах in vitro, а также на фиксированных образцах. Конечно, нежелательно на одном графике изображать различные величины, полученные при неидентичных условиях на образцах различного вида, однако ограниченность информации исключает другую возможность.
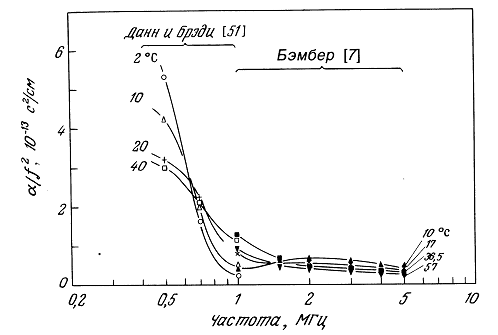
Рис. 4.11. Изотермические зависимости параметра ![]() от частоты для тканей центральной нервной системы. На частотах ниже 1 МГц представленные зависимости характеризуют поглощение звука в спинном мозге мыши [50], выше 1 МГц эти графики соответствуют затуханию звука в фиксированном мозге коровы [10]. Результаты Робинсона и Лили [187] для затухания в мозге кошки на частоте 4,2 МГц в интервале температур от 30 до 50 °С, а также данные Кремкау и др. [118] для мозга человека согласуются с представленными зависимостями. Данные этих авторов мы не приводим, чтобы не загромождать рисунок.
от частоты для тканей центральной нервной системы. На частотах ниже 1 МГц представленные зависимости характеризуют поглощение звука в спинном мозге мыши [50], выше 1 МГц эти графики соответствуют затуханию звука в фиксированном мозге коровы [10]. Результаты Робинсона и Лили [187] для затухания в мозге кошки на частоте 4,2 МГц в интервале температур от 30 до 50 °С, а также данные Кремкау и др. [118] для мозга человека согласуются с представленными зависимостями. Данные этих авторов мы не приводим, чтобы не загромождать рисунок.
Специфика представленных на рис. 4.11 графиков заключается в том, что, хотя центральная частота области низкочастотной релаксации смещается в сторону больших значений с ростом температуры, усредненная амплитуда релаксации является, по-видимому, спадающей функцией температуры. Кроме того, форма релаксационной кривой меняется при изменении температуры [30]. В настоящее время все эти факты не имеют объяснения.
По данным работы [112] в частотном диапазоне 1,4 — 4,5 МГц затухание звука в костях увеличивается с ростом температуры. В работе [30] высказывалось предположение, что это может быть связано с небольшими отрицательными значениями углового коэффициента зависимости ln(![]() ) от f в костях. В то же время автор работы [16] считает, что подобное поведение может служить и доказательством того, что механизм затухания звука связан с явлением рассеяния.
) от f в костях. В то же время автор работы [16] считает, что подобное поведение может служить и доказательством того, что механизм затухания звука связан с явлением рассеяния.
4.5.2.6. Влияние структурных компонентов ткани
В работах [48, 84, 164, 182] было показано, что для большинства биологических тканей (за исключением таких тканей, как жир, легкие и кости) можно найти приближенные эмпирические соотношения, описывающие взаимосвязь между акустическими свойствами тканей и концентрациями определенных структурных компонентов. В частности, при переходе от жидкостей типа крови к сухожилиям и хрящам в них возрастает содержание структурных белков (коллагена) и этот рост коррелирует с увеличением затухания и скорости звука. В паренхиматозных тканях, характеризующихся сравнительно малым содержанием коллагена, затухание и скорость звука зависят, по-видимому, в основном от общего содержания глобулярных белков. Не исключено также, что величины этих параметров обратно пропорциональны содержанию воды в тканях (см. также работу [14]). Иногда высказывалось предположение, что коллаген является важным в акустическом плане элементом ткани, особенно в отношении рассеяния звука [63]. Недавно было показано [83], что удельное поглощение и скорость звука в водном растворе коллагена соответственно почти в 4 и 2 раза превышают значения этих параметров в растворе глобулярных белков (на единицу концентрации). Было также установлено, что рост содержания коллагена связан с высокими уровнями затухания ультразвука, свидетельствующими о возможности патологии, например, в случае некоторых первичных опухолей молочной железы [115], а также при инфаркте миокарда в период рубцевания [150].
В ряде тканей важную роль играет также содержание жира главным образом в силу очень низких значений скорости звука в жировой ткани (см. гл. 5). Различные исследования показывают, что рост содержания жира в печени может привести к уменьшению скорости звука даже при малом содержании воды, а также к возрастанию коэффициентов затухания и рассеяния [11, 14, 69, 160, 197, 205]. Те ткани, где содержится много жира и имеется большое число границ раздела между жировой и нежировой компонентами, например, ткани молочной железы [9], будут характеризоваться в среднем малой скоростью звука и большими значениями коэффициентов затухания и рассеяния в сравнении с другими мягкими тканями.
Вопросы, связанные с исследованием затухания и поглощения продольных ультразвуковых волн в различных биологических средах и тканях, представляются чрезвычайно сложными и очень далеки от понимания. В настоящее время отсутствуют какие-либо удовлетворительные объяснения наблюдаемых зависимостей затухания звука как от физических параметров (т. е. частоты, температуры и так далее), так и от свойств самой ткани.
Большие трудности возникают при определении коэффициента затухания и вряд ли кому-либо удалось измерить его с высокой точностью. При использовании разных методов измерения для одних и тех же образцов получаются различные значения коэффициента затухания. Хотя такое расхождение результатов обусловлено главным образом влиянием систематических погрешностей измерения, не следует думать, что какой-либо метод, характеризующийся наименьшими погрешностями, во всех случаях будет давать наиболее правильные оценки акустических потерь (например, ультразвуковая визуализация).
Мы не ставили себе здесь задачу обсудить все многочисленные практические выводы и рекомендации, которые вытекают из анализа явлений и данных, рассмотренных в этой и следующей главах. Простыми следствиями являются невозможность получения с помощью ультразвукового зондирования изображений легочных или костных структур или же тех структур, которые лежат за этими органами, а также легкость идентификации заполненных жидкостью полостей. Более сложные случаи —это искажения ультразвукового пучка и ухудшение пространственной разрешающей способности, обусловленные зависимостью затухания от частоты [67], а также возможность использования накопленных данных для выбора оптимальной частоты при акустической визуализации какого-либо конкретного органа или для создания акустических фантомов, подходящих для контрольных и проверочных испытаний.
В настоящее время на основе методов измерения in vivo, рассмотренных в разд. 4.4.1.3, создаются возможности разработки систем визуализации и анализа свойств биологических тканей более высокого уровня, обеспечивающих получение количественной информации. О таких системах пойдет речь в гл. 9 и 10. В недавно вышедшей обзорной работе Джонса и Лимана [108] собраны данные о результатах измерения затухания ультразвука in vivo и зависимости этих результатов от патологического состояния организма.
1. Ahuja, A. S. (1979) Tissue as a Voigt body for propagation of ultrasound. Ultrasonic Imaging, 1, 136—143.
2. Ahuja, A. S. & Handel, W. R. (1978) Effects of particle shape and orientation on propagation of sound in suspensions. J. acoust. Soc. Amer. 63, 1074—1080.
3. Akiyama, I., Nishida, Y., Nakajima, M., & Yuta, S. (1983) On the measurement of frequency dependent attenuation in biological tissue using broadband pulsed ultrasound. IEEE Ultrasonic Symposium Proc. Vol. 2, Cat. No. 83CH1947-1, 800—805.
4. Altman, P. L. & Dittmer, D. S. (1972) Biology data book (2nd Ed.) Vol. I, FASEB, Washington, D. C, p. 392.
5. Andreae, J. H., Bass, R., Heasell, E. L., & Lamb J. (1958) Pulse techniques for measuring ultrasonic absorption in liquids. Acustica, 8, 131.
6. Baboux, J. C, Lakestani, F., Fleischmann, Perdix, M., Guillaud, C, and Goutte, R. (1976). An ultrasonic spectroscopy device: application to tissue differentiation. Proc. 2nd European Congress on Ultrasonics in Medicine, Kazner, E. et al. (Eds), American Elsevier Publishing Co., Inc., N. Y., pp. 108—114.
7. Bamber, J. C. (1979) Ultrasonic characterization of structure and pathology in human soft tissues. PhD Thesis, University of London.
8. Bamber, J. C. (1981) Letter: Ultrasonic attenuation in fresh human tissues. Ultrasonics, July 1981, 187—188.
9. Bamber, J. C. (1983) Ultrasonic propagation properties of the breast, In: Ultrasonic examinauon of the breast, (eds. Jellins, J. & Kobayashi, T.) John Wiley & Sons Ltd., Chichester, 37—44.
10. Bamber, J. C. & Hill, C. R. (1979) Ultrasonic attenuation and propagation speed in mammalian tissue as a function of temperature. Ultrasound Med. Biol. 5, 149—157.
11. Bamber, J. C. & Hill, C. R. (1981) Acoustic properties of normal and cancerous human liver: Dependence on pathological condition. Ultrasound Med. Biol. 7, 121—133.
12. Bamber, J. C, Hill, C. R., Fry, M. J., & Dunn, F. (1977) Ultrasonic attenuation and backscattering by mammalian organs as a function of time after excision. Ultrasound Med Biol. 3, 15—20.
13. Bamber, J. C, Hill, C. R., King, J. A., & Dunn, F. (1979) Ultrasonic propagation through fixed and unfixed tissues. Ultrasound Med Biol. 5, 159—165.
14. Bamber, J. C, Hill, C. R., & King, J. A. (1981) Acoustic properties of normal and cancerous human liver — II. Dependence on tissue structure. Ultrasound Med. Biol. 7, 135—144.
15. Bamber, J. C. & Nassiri, D. K. (1985) Effect of gaseous inclusions of the frequency dependence of ultrasonic attentuation in liver. Ultrasound Med. Biol. 11, 293—298.
16. Barger, J. E. (1979) Attenuation and dispersion of ultrasound in cancellous bone, In: Ultrasonic tissue characterisation II. M. Linzer (ed), National Bureau of Standards, Spec. Publ. 525, US Govt. Printing Office, Washington, D. C, pp. 197—201.
17. Bergmann, P. G. (1949) The wave equation in a medium with a variable index of refraction. J. acoust. Soc. Amer. 7, 329—333.
18. Beyer, R. T. (1974) Nonlinear acoustics. Naval Ship Systems Command, U.S. Department of the Navy.
19. Beyer, R. T. (1965) Nonlinear Acoustics, In: Physical acoustics: principles and methods, (ed. Mason, W. P.) Vol. II. — Part B, Chap. 10, New York and London, Academic Press, pp. 231—264.
20. Beyer, R. T. & Letcher, S. V. (1969) Physical ultrasonics. New York and London, Academic Press.
21. Bhadra, Т. C. & Roy, B. (1975) Attenuation of ultrasonic energy in liquids by the streaming method. Ultrasonics International Conference Proc, Guildford, IPC Science and Technology Press Ltd., pp. 253—256.
22. Bhagat, P., Hajjar, W., & Kadaba, M. (1976) Measurement of the acoustic properties of a nerve-muscle preparation as a function of physiological state. Ultrasonics, Nov. '76, 283—285.
23. Bjorno, L. (1975) Non-linear ultrasound — a review. Ultrasonics International Conference Proc, Guildford, IPC Science and Technology Press Ltd., pp. 110—115.
24. Braddick, H. J. J. (1965) Vibrations, waves, and diffraction. McGraw-Hill, London, New York, Toronto, Sydney.
25. Brendel, K. & Ludwig, G. (1975) Measurement of ultrasonic diffraction loss for circular transducers. Acoustica, 32, 110.
26. Busse, L. J. & Miller, J. G. (1981) Detection of spatially nonuniform ultrasonic radiation with phase sensitive (piezoelectric) and phase insensitive (acoustoelectric) receivers. J. acoust. Soc. Amer. 70, 1377—1386.
27. Calderon, C, Vilkomerson, D., Mezrich, R., Etzold, K. F, Kingsley, В., & Haskin, M. (1976) Differences in the attenutation of ultrasound by normal, benign, and malignant breast tissue. J. Clinical Ultrasound, 249—254.
28. Campbell, J. A. & Waag, R. C. (1984) Measurements of calf liver ultrasonic differential and total scattering cross-sections. J. acoust. Soc. Amer. 75, 603—611.
29. Carson, P. L., Meyer, C. R., & Scherzinger, A. L. (1981) Breast imaging in coronal planes with simultaneous pulse echo and transmission ultrasound. Science, 214, 1141—1143.
30. Carstensen, E. L. (1979) Absorption of sound in tissue, in "Ultrasonic tissue characterization II" (ed. M. Linzer), National Bureau of Standards, Spec. Publ. 525, U.S. Govt. Printing Office, Washington, D.C. pp. 29—40.
31. Carstensen, E. L., Li, K., & Schwan, H. P. (1953) Determination of the acoustic properties of blood and its components. I. acoust. Soc. Amer. 25, 286—289.
32. Carstensen, E. L., & Schwan, H. P. (1959) Absorption of sound arising from the presence of intact cells in blood. J. acoust. Soc Amer., 31, 185—189.
33. Carstensen, E. L., Law, W. K., McKay, N. D., & Muir, T. G. (1980) Demonstration of nonlinear acoustical effects at biomedical frequencies and intensities. Ultrasound Med. Biol. 6, 359-368.
34. Chivers, R. C. & Hill, C. R. (1975) Ultrasonic attenuation in human tissue. Ultrasound Med. Biol. 2, 25—29.
35. Chivers, R. C. & Parry, R. J. (1978) Ultrasonic velocity and attenuation in mammalian tissues. J. acoust. Soc Amer. 63, 940—953.
36. Christensen, R. M. (1971) Theory of viscoelasticity, Academic Press, New York.
37. Cloostermans, M. J. Т. M. & Thijssen, J. M. (1938) A beam corrected estimation of the frequency dependent attenuation of biological tissues from backscattered ultrasound. Ultrasonic Imaging, 5, 136—147.
38. Colombati, S. & Petralia, S. (1950) Assorbimento di ultrasuoni in tessunti animali.
La Ricerca Scientifica Anno, 20°-N.l-2, 71—78.
39. Crosby, В. C. & Mackay, R. S. (1978) Some effects of time post-mortem on ultrasonic transmission through tissue under different modes of handling. IEEE Trans. Biomed. Eng. BME-25, 91—92.
40. Duback, D. W., Frizzell, L. A., & O'Brien, Jr. W. D. (1979) An automated system for measurement of absorption coefficients using the transient thermoelectric technique, 1979 Ultrasonics Symposium Proc. IEEE Cat. No. 79CH 1482-92U, 388—391.
41. Duck, F. A. & Hill, C. R. (1979) Mapping true ultrasonic backscatter and attenuation distributions in tissue: a digital reconstruction approach, in: Ultrasonic tissue characterization II. (ed. M. Linzer), National Bureau of Standards Spec. Publ. 525, U.S. Govt. Printing Office, Washington, D. C. pp. 247—251.
42. Duff in, W. J. (1968) Advanced electricity and magnetism. London, McGraw-Hill Ltd. (pp. 172—174).
43. Dumas, G. A., Thiry, P. S., & Drouin, G. (1983) Interferometric measurement method of ultrasonic attenuation in small liquid samples. IEEE Trans. Son. Ultrason., 30, 59—68.
44. Dunn, F. (1962) Temperature and amplitude dependence of acoustic absorption in tissue. J. acoust. Soc. Amer. 34(10), 1545—1547.
45. Dunn, F. (1965) Ultrasonic absorption by biological materials, in, Ultrasonic energy: biological investigations, and medical applications, (ed. E. Kelly), 51—65. University of Illinois Press, Urbana.
46. Dunn, F. (1974) Attenuation and speed of sound in lung. J. acoust. Soc. Amer. 56, 1638—1639.
47. Dunn, F. (1975) Ultrasonic attenuation, absorption and velocity in tissues and organs, in: Seminar on ultrasonic tissue characterization, (ed. M. Linzer), Washington, D. C, N.B.S. Special Publ. 453, pp. 21—28.
48. Dunn, F. (1976) Ultrasonic attenuation, absorbtion and velocity in tissues and organs in: Ultrasonic tissue characterization, (ed. M. Linzer), Washington, D.C., N.B.S. Special Publication 453, U.S. Govt. Printing Office, 21—28.
49. Dunn, F. (1981), частное сообщение.
50. Dunn, F. & Brady, J. K. (1974) Temperature and frequency dependence of ultrasonic absorption in tissue, in, Proc. Sth Intl. Congress on Acoustics, Goldcrest Press, Trowbridge, Vol. I,, p. 366c.
51. Dunn, F. & Beyer, J. E. (1962) Generation and detection of ultra-highfrequency sound in liquids. J. acoust. Soc. Amer. 34, No. 6, 775—778.
52. Dunn, F. & Fry, W. J. (1961) Ultrasonic absorption and reflection by lung tissue. Phys. Med. Biol., 5, 401—410.
53. Dunn, F., Edmonds, P. D., & Fry, W. J. (1969) Absorption and dispersion of ultrasound in biological media, in: Biological engineering (ed. Schwan, H. P.), New York, McGraw-Hill, pp. 205—332.
54. Dunn, F., Law, W. K., & Frizzell, L. A. (1982) Nonlinear ultrasonic propagation in biological media. Br. J. Cancer 45, Suppl. V, 55—58.
55. Dunn, D. & O'Brien, W. D. (1977) (Editors) Ultrasonic biophysics. Benchmark papers in acoustics, Vol. 7, Dowden, Hutchinson and Ross.
56. Dunn, F., & O'Brien, W. D. (1978) Absorption and dispersion, in: Ultrasound: its application in medicine and biology (ed. Fry, F. J.) Amsterdam, Elsevier, Ch. 3, p. 393.
57. von Esche, R. (1952) Untersuchungen zur Ultraschallabsorption in tierischen Geweben und Kunststoffen. Akustische Biehefte, 1, 71—74.
58. Eggers, F. & Funck, Th. (1973) Ultrasonic measurements with mililiter liquid samples in the 0.5—100 MHz range. Rev. Sci. Instrum., 44, 969—977.
59. Eggers, F., Funck, Th., & Richmann, К. H. (1981) Ultrasonic absorption measurements with a millilitre short-path pulse cell. J. Phys. E: Sci. Instrum. 14, 113—116.
60. Eggleton, R. C. & Whitcomb, J. A. (1979) Tissue simulators for diagnostic ultrasound, in: Ultrasonic tissue characterization II. (ed. M. Linzer) National Bureau of Standards, Spec. Publ. 525, U.S. Govt. Printing Office, Washington, D. C. pp. 327—336.
61. von Ehrenberg, R., Winnecken, H. G., & Biebricher, H. (1954) "Der Altemsgang des Bindegewebes in menschlichen Organen", Zeitschrift fur Naturforschung, 9b, 492—495.
62. Ferry, J. D. (1961) Viscoelastic properties of polymers. John Wiley & Sons, NY. and London.
63. Fields, S. & Dunn, F. (1973) Correlation of echographic visualizability of tissue with biological composition and physical state. J. acoust. Soc. Amer., 54, 809—812.
64. Fink, M. A. & Cardoso, J. F. (1984) Diffraction effects in pulse echo measurement. IEEE Trans. Sonics and ultrasonics, SU-31, 313—329.
65. Fink, M., Hottier, F., & Cardoso, J. F. (1983) Ultrasonic signal processing for in vivo attenuation measurement: short time Fourier analysis. Ultrasonic Imaging, 5, 117—135.
66. Flax, S. W, Pelc, N. J., Glover, G. H., Gutmann, F. D., & McLachlan, M. (1983) Spectral characterization and attenuation measurements in ultrasound. Ultrasonic Imaging, 5, 95—116.
67. Foster, F. S. & Hunt, J. W. (1979) Transmission of ultrasound beams through human tissue—focussing and attenuation studies. Ultrasound Med. Biol 5, 257—268.
68. Foster, F. S., Strban, M., & Austin, G. (1984) The ultrasound macroscope Initial studies of breast tissue. Ultrasonic Imaging, 6, 243—261.
69. Freese, M. & Lyons, E. A. (1977) Ultrasonic backscatter from human liver tissue: its dependence of frequency and protein/lipid composition. J. Clin. Ultrasound 5, 307—312.
70. Freese, M. & Makow, D. (1968) Ultrasonic backscatter in fresh and thawed animal tissue. J. Fish. Res. Bd., Canada, 25, 605—607.
71. Frizzell, L. A. (1976) Ultrasonic heating of tissues. PhD Thesis, University of Rochester.
72. Frizzell, L. A., Carstensen, E. L., & Davis, D. (1979) Ultrasonic absorption in liver tissue. J. acoust. Soc. Amer. 65, 1309—1312.
73. Froeiich, B. (1977) A simple apparatus for automatic pulse echo tracking. J. Phys. E. Scient. Inst., 10, 210—211.
74. Fry, W. J. (1952) Mechanism of acoustic absorption in tissue. J. acoust. Soc. Amer. 24, 412—415.
75. Fry, W. J. & Dunn, F. (1962) Ultrasound analysis and experimental methods in biological research, in: Physical techniques in biological research Chapt. 4, Academic Press, New York, pp. 261—394.
76. Fry, W. J. & Fry, R. B. (1954a) Determination of absolute sound levels and acoustic absorption coefficients by thermocouple probes — theory. /. acoust. Soc. Amer. 26, 294—310.
77. Fry, W. J. & Fry, R. B. (1954b) Determination of absolute sound levels and acoustic absorption coefficients by thermoelectric probes—experiment. J. acoust. Soc. Amer. 26, 311—317.
78. Gamble, R. C. & Schimmel, P. R. (1978) Nano-second relaxation processes of phos pholipid bilayers in the transition zone. Proc. Natl. Acad. Sci. USA, 75, 3011—3014.
79. Gammell, P. M., Le Croisette, D. H., & Heyser, R. C. (1979) Temperature and frequency dependence of ultrasonic attenuation in selected tissues. Ultrasound Med. Biol. 5, 269—277.
80. Glueck, R. M., Mottley, J. G., Sobel, В. E., Miller, J. G., & Perez, J. E. (1985) Changes in ultrasonic attenuation and backscatter of muscle with state of contraction. Ultrasound Med. Biol., 11, 605—610.
81. Goldman, D. E. & Hueter, T. F. (1956) Tabular data of the velocity and absorption of high frequency sound in mammalian tissues. J. acoust. Soc. Amer. 28, 35—37.
82. Goobermann, G. L. (1968) Ultrasonics theory and application. English Universities Press, London, Ch. 8.
83. Goss, S. A. & Dunn, F. (1980) Ultrasonic propagation properties of collagen. Phys. Med. Biol. 25, 827—837.
84. Goss, S. A., Frizzell, L. A. & Dunn, F. (1980) Dependence of the ultrasonic properties of biological tissue on constituent proteins. J. acoust. Soc. Amer. 67, 1041—1044.
85. Goss, S. A. & Fry, F. J. (1981) Nonlinear acoustic behaviour in focussed ultrasonic fields: observations of intensity dependent absorption in biological tissue. IEEE Trans. Sonics Ultrason. SU-28, pp. 21—26.
86. Goss, S. A., Cobb, J. W., & Frizzell, L. A. (1977) Effect of beam width and thermocouple size on the measurement of ultrasonic absorption using the thermocouple technique. 1977 Ultrasonics Symposium Proc. IEEE Cat. No. 77CH 1264-1SU, 206—211.
87. Goss, S. A., Johnston, R. L., & Dunn, F. (1978) Comprehensive compilation of empirical ultrasonic properties of mammalian tissues. J. acoust. Soc. Amer. 64, 423—457.
88. Goss, S. A., Johnston, R. L., & Dunn, F. (1980) Compilation of empirical ultrasonic properties of mammalian tissues. II. J. acoust. Soc. Amer. 68, 93—108.
89. Goss, S. A., Johnston, R. L., Maynard, V., Nider, L., Frizzell, L. A., O'Brien, Jr. W. d., & Dunn, F. (1979) Elements of tissue characterization, Part II. Ultrasonic propagation parameter measurements, in: Ultrasonic tissue characterization II. (Ed. M. Linzer, NBS Spec. Publ. 525, Washington, D.C. U.S. Govt. Printing Office, pp. 43—51.
90. Goss, S. A., Frizzell, L. A., & Dunn, F. (1979a) Ultrasonic absorption and attenuation in mammalian tissues. Ultrasound Med. Biol. 5, 181—186.
91. Greenleaf, J. F. & Bahn, R. C. (1981) Clinical imaging with transmission ultrasonic computerized tomography. IEEE Trans. BME-28, No. 2, 177—185.
92. Hall, L. (1948) The origin of ultrasonic absorption in water. Phys. Rev., 73, 775.
93. Hall, D. N. & Lamb, J. (1959) Measurement of ultrasonic absorption in liquids by
the observation of acoustic streaming. Proc. Phys. Soc. 73, 354—356.
94. Hammes, G. G. & Roberts, P. B. (1970) Ultrasonic attenuation measurements in phospholipid dispersions. Biochim. Biophys. Acta 203, 220—227.
95. Haran, M. E. (1981) Distortion of finite amplitude ultrasound in tissue. (Abstract), 101st Meeting of the Acoust. Soc. Amer. J. acoust. Soc. Amer. Suppl. 1, 69, S4.
96. Hawley, S. A. & Dunn, F. (1969) Ultrasonic absorption in aqueous solutions of dextran. J. Chem Phys. 50, 3523—3526.
97. Hertzfeld, K. F. & Litovitz, T. A. (1959) Absorption and dispersion of ultrasonic waves. Academic Press, New York.
98. Heimburger, R. F., Fry, F. J., Franklin, T. D., Sanghvi, N. T, Gardner, G., & Muller, J. (1976) Two dimensional ultrasound scanning of excised brains—I. normal anatomy. Ultrasound Med. Biol., 2, 279—285.
99. Heyser, R. C. & Le Croisette, D. H. (1974) A new ultrasonic imaging system using time delay spectrometry. Ultrasound Med Biol. 1, 119—131.
100. Hill, C. R. (1975) Echoes from human tissues. Proc. Ultrasonics International, IPC Science and Technology Press, Guildford, 20—22.
101. Hill, C. R., Chivers, R. C, Huggins, R. W., & Nicholas, D. (1978) Scattering of ultrasound by human tissues. Ultrasound: Its application in medicine and biology. Fry, F. J. (Ed) Elsevier, Amsterdam, Ch. 9.
102. Holasek, E., Jennings, W. D., Sokollu, A., & Purnell, E. W. (1973) Recognition of tissue patterns by ultrasonic spectroscopy. Proc. IEEE Ultrasonics Symposium, Monterey, IEEE. New York, 73—76.
103. Hueter, T. F. (1952) Messung der ultraschallabsorption in Menschlichen Schadelknochen und ihre Abhangigkeit von der Frequenz. Naturwissen-schaften 39, 21. (Translation to be found in Ultrasonic Biophysics, (Dunn, F. and O'Brien, Jr. W. D., eds.) Dowden, Hutchinson and Ross, Inc.
104. Hueter, T. F. (1958) Visco-elastic losses in tissue in the ultrasonic range. Wright Air Development Centre, Wlight-Patterson AFB, Ohio, Tech. Rept. No. 57—706, ASTIA, Doc. No. AD142171.
105. Insana, M. I., Zagzebski, J., & Madsen, E. (1983) Improvements in the spectral difference method for measuring ultrasonic attenuation. Ultrasonic Imaging 5, 331—345.
106. Javanaud, C, Rahalkar, R. R., & Richmond, P. (1984) Measurement of speed and attenuation of ultrasound in egg white and egg yolk. J. acoust. Soc. Amer., 76, 670—675.
107. Johnston, R. L., Goss, S. A., Maynard, V., Brady, J. K., Frizzell, L. A., O'Brien, W. D., & Dunn, F. (1979) Elements of tissue characterization, Part I. Ultrasonic propagation properties, in: Ultrasonic tissue characterization II. (ed. M. Linzer). National Bureau of Standards, Spec. Publ. 525, U.S. Govt. Printing Office, Washington, D.C. 19—27.
108. Jones, J. P. & Leeman, S. (1984) Ultrasonic tissue characterization: a review. Acta Electronica. 26, 3—31.
109. Kelly Fry, E., Sanghairi, N. T, Fry, F. J., & Gallager, H. S. (1979) Frequency dependent attenuation of malignant breast tumours studied by the fast Fourier transform technique, in: Ultrasonic tissue characterization II. (ed. M. Linzer) National Bureau of Standards, Spec. Publ. 525, U.S. Govt. Printing Office, Washington, D.C. 85—91.
110. Kessler, L. W. (1973) VHF ultrasonic attenuation in mammalian tissue. J. acoust. Soc. Amer. 53, 1759—1760.
111. Kessler, L. W., Hawley, S. A., & Dunn, F. (1971) Semi-automatic determination of ultrasonic velocity and absorption in liquids. Acustica, 24, 105—107.
112. Kishimoto, T. (1958) Ultrasonic absorption in bones. Acustica 8, 179—180.
113. Kjosnes, N. I. (1976) A technique for the rigid determination of ultrasonic propagation velocity in mammalian tissues, solids, and liquids. Thesis, Wake Forest College, Bowman-Gray School of Medicine, Winston-Salem, N. C.
114. Klepper, J. R. & Brandenburger, G. H. (1981) Application of phaseinsensitive detection and frequency-dependent measurements to ultrasonic attenuation tomography. IEEE Trans. Biomed. Eng. BME-28, 186—201.
115. Kobayashi, T. (1979) Diagnostic ultrasound in breast cancer, analysis of retrotumorous echopatterns correlated with sonic attenuation by cancerous connective tissue. /. Clin. Ultrasound, 7, 471—479.
116. Kol'tsova, I. S., Mikhailov, I. G., & Trofimov, G. S. (1980) Structural acoustic relaxation in suspensions of interacting particles. Soc. Phys. Acoust. 26, 319—322.
117. Kossoff, G., Kelly Fry, E., & Jellins, J. (1973) Average velocity of ultrasound in the human female breast. J. acoust. Soc. Amer. 53, 1730—1736.
118. Kremkau, F. W., Barnes, R. W., & McGraw, C. P. (1981) Ultrasonic attenuation and propagation speed in normal human brain. J. acoust. Soc. Amer. 70, 29—38.
119. Kremkau, F. W. & Carstensen, E. L. (1972) Macromolecular interaction in sound absorption, in: Interaction of ultrasound and biological tissues—Workshop Proc. (Ed. Reid, J. M. and Sikov, M. R.) DHEW publication (FDA) 73-8008 BRH/DBE 73-1 (U.S. Govt. Printing Office, Washington, D.C), 37—42.
120. Kremkau, F. W. & Carstensen, E. L. (1973) Macromolecular interaction in the absorption of ultrasound in fixed erythrocytes. J. acoust. Soc. Amer. 5, 1448—1451.
121. Kremkau, F. W. & Cowgill, R. W. (1984) Biomolecular absorption of ultrasound. I. Molecular weight. /. acoust. Soc. Amer. 76, 1330—1335.
122. Kuc, R. & Regula, D. (1984) Diffraction effects in reflected ultrasound spectral estimates. IEEE Trans. Biomed. Eng. BME-31, 527—545.
123. Kuc, R. & Schwartz, M. (1979) Estimating the acoustic attenuation coefficient slope for liver from reflected ultrasound signals. IEEE Trans. Sonics and Ultrasonics, SU-26, 353—362.
124. Lakestani, F., Baboux, J. C, & Fleischmann, P. (1975) Broadening the bandwidth of piezoelectric transducers by means of transmission lines. Ultrasonics, July 1975, 176—180.
125. Lamb, J. (1965) Thermal relaxation in liquids. Physical acoustics Vol. 2A. Mason, W. P. (Ed.), Academic Pres, New York, 203—280.
126. Lang, J., Zana, R., Gairard, В., Dale, G., & Gros, Ch. M. (1978) Ultrasound absorption in the human breast cyst liquids. Ultrasound med. Biol. 4, 125—130.
127. Law, W. K., Frizzell, L. A., & Dunn, F. (1981) Ultrasonic determination of the nolinearity parameter B/A for biological media. J. acoust. Soc. Amer. 39, 1210—1212.
128. Law, W. K., Frizzell, L. A., & Dunn, D. (1985) Determination of the nonlinearity parameter B/A of biological media. Ultrasound Med. Biol., 11, 307—318.
129. Leeman, S., Ferrari, L., Jones, J. P., & Fink, M. (1984) Perspectives on attenuation estimation from pulse-echo signals. IEEE Trans. Sonics and Ultrasonics, SU-31, 354—361.
130. Lele, P. P., Mansfield, А. В., Murphy, A. I., Namery, J., & Senapati, N. (1976) Tissue characterization by ultrasonic frequency-dependent attenuation and scattering. Proc. Seminar on Ultrasonic Tissue Characterization, (ed. Linzer, M.). National Bureau of Standard, Spec. Publ. 453, U.S. Govt. Printing Office, Washington, D.C. 167—196. 131 Lele, P. P. & Senapati, N. (1977) The frequency spectra of energy back-scattered and attenuated by normal and abnormal tissue. In: Recent advances in ultrasound in biomedicine Vol. I. (ed. White, D. N.) Research Studies Ross, Oregon, 55—85.
132. Levi, S. & Keuwez, J. (1979) Tissue characterization in vivo by differential attenuation measurements, in: Ultrasonic tissue characterisation II. (ed. Linzer, M.) National Bureau of Standards, Spec. Publ. 525, U.S. Govt, Printing Office, Washington, D.C. 121—124.
133. Litovitz, T. A. & Carnevale, E. H. (1958) Effect of pressure on ultrasound relaxation in liquids, II. J. acoust. Soc. Amer. 30. 134—136.
134. Litovitz, T. A. & Davis, С. M. (1965) Structural and shear relaxation in liquids. Physical acoustics Vol 2A, Mason, W. P. (Ed.), Academic Press, New York, 281—349.
135. Lizzi, F. L., Kate, L., St. Louis, L., & Coleman, D. J. (1976) Applications of spectral analysis in medical ultrasonography. Ultrasonics, March '76, 77—80.
136. Lomonaco, A., Kline, P., Halpern, S., & Leopold, G. (1975) Nuclear medicine and ultrasound: correlation in diagnosis of disease of liver and biliary tract. Sem. Nucl. Med. 5, 307—324.
137. McNeely, W. D. & Noordergraaf, A. (1981) In vivo attenuation measurement in preand postmortem muscle using ultrasound. IEEE Trans. Sonics and Ultrason. SU-28, 237—241.
138. McQueen, D. (1977) Applications of a simple theory of acoustic motion of fibrous networks in viscous media. Ultrasonics, 15, 175—178.
139. McSkimin, H. J. (1964) Ultrasonic methods of measuring the mechanical properties of liquids and solids, in: Physical acoustics: principles and methods (ed. Mason, W. P.), Vol. I — Part A, Ch. 10, New York and London, Academic Press, pp. 271—334.
140. Madigosky, W. M., Rosenbaum, I., & Lucas, R. (1981) Sound velocities and B/A in fluorocarbon fluids and in several low density solids. J. acoust. Soc. Amer. 69, 1639—1643.
141. Maklad, N. F, Ophir, J., & Balsara, V. (1984) Attenuation of ultrasound in normal liver and diffuse liver disease in vivo. Ultrasonic Imaging 6, 117—125.
142. Marcus, P. W. & Carstensen, E. L. (1975) Problems with absorption measurements of inhomogeneous solids. J. acoust. Soc. Amer. 58, 1334—1335.
143. Markham, J. J., Beyer, R. T, & Lindsay, R. D. (1951) Absorption of sound in fluids. Rev. mod. Phys. 23, 353—411.
144. Mason, W. P. (1958) Physical acoustics and the properties of solids. Van Nostrand, New York.
145. Matheson, A. J. (1971) Molecular acoustics. London, John Wiley & Sons Ltd.
146. Maynard, V. M., Magin, R. L., & Dunn, F. (1985) Ultrasonic absorption and permiability for liposomes near phase transition. Chemistry and Physics of Lipids, 37, 1—12.
147. Mercier, N. (1975) Ultrasonic classification of metals by grain size. In: Ultrasonics International 1975 Conf. Proc. IPC Science and Technology Press, Guildford, p. 64—67.
148. Miles, C. A. & Cutting, C. L. (1974) Technical note: Changes in the velocity of ultrasound in meat during freezing. /. Fd. Technol. 9, 119—122.
149. Miles, C. A. & Fursey, G. A. (1974) A note on the velocity of ultrasound in living tissue. Amin. Prod. 18, 93—96.
150. Miller, J. G., Yuhas, D. E., Mimbs, J. W, Dierker, S. В., Busse, L. J., Laterra, J. J., Weiss, A. N., & Sobel, В. E. (1976) Ultrasonic tissue characterization: correlation between biochemical and ultrasonic indices of myocardial injury. Ultrasonics Symp. Proc. IEEE Cat. No. 76-CH1120-5SU, 33—43.
151. Mitaku, S. (1981) Ultrasonic studies of lipid bilayer phase transition. Mol. Cryst. Liq. Cryst., 70, 21—28.
152. Moore, W. J. (1962) Physical chemistry, 4th edition, Longmans, Green and Co. Ltd., London. Ch. 8.
153. Morfey, C. L. (1968) Sound attenuation by small particles in a fluid. J. Sound Vib. 8, 156—170.
154. Morse, P. M. & Ingard, K. U. (1968) Theoretical acoustics, McGraw-Hill, New York.
155. Mountford, R. A. & Halliwell, M. (1973) Physical sources of registration errors in pulse-echo ultrasound systems. Path II-beam deformation, deviation and divergence. Med. Biol. Eng., January 1973, 33—38.
156. Mountford, R. A. & Wells, P. N. T. (1972a) Ultrasonic liver scanning: the quantitative analysis of the normal A-scan. Phys. Med. Biol. 17, 1—25.
157. Mountford, R. A., & Wells, P. N. T. (1972b) Ultrasonic liver scanning: the A-scans in the normal and cirrhosis. Phys. Med. Biol. 17, 261—269.
158. Muir, T. G. & Carstensen, E. L. (1980) Prediction of nonlinear acoustic effects at biomedical frequencies and intensities. Ultrasound Med. Biol. 6, 345—357.
159. Narayana, P. A. & Ophir, J. (1983a) Spectral shifts of ultrasonic propagation: a study of theoretical and experimental models. Ultrasonic Imaging 5, 22—29.
160. Narayana, P. A. & Ophir, J. (1983b) On the frequency dependence of attenuation in normal and fatty liver. IEEE Trans. Sonics and Ultrasonics, SU-30, 379—383.
161. Nassiri, D. K. & Hill, C. R. (1986a) The differential and total bulk acoustic scattering cross sections of some human and animal tissues. /. acoust. Soc. Amer. 76, 2034—2047.
162. Nassiri, D. K. & Hill, C. R. (1986b) The use of acoustic scattering measurements to estimate structural parameters of human and animal tissues. J. acoust. Soc. Amer. 76, 2048—2054.
163. Nassiri, D. K., Nicholas, D. N. & Hill, C. R. (1979) Attenuation of ultrasound in skeletal muscle. Ultrasonics 17, 230—232.
164. O'Brien, Jr. W. D. (1977) The relationship between collagen and ultrasonic attenuation and velocity in tissue. Ultrasonics International 1977 Conference Proc. IPC Business Press, Guildford, 194—205.
165. O'Donnell, M. (1983) Effects of diffraction on measurements of the frequency dependence of ultrasonic attenuation. IEEE Trans. Biomed. Eng. BME-30, 320—326.
166. O'Donnell, M. & Miller, J. G. (1979) Mechanisms of ultrasonic attenuation on soft tissue. In: Ultrasonic tissue characterization. II. (ed. Linzer, M.), NBS spec, publ. 525, Washington, D.C. 37—40.
167. O'Donnell, M., Jaynes, E. Т., & Miller, J. G. (1978) General relationships between ultrasonic attenuation and dispersion. J. acoust. Soc. Amer. 63, 1935—1937.
168. O'Donnell, M., Jaynes, E. Т., & Miller, J. G. (1981) Kramers-Kronig Relationships between ultrasonic attenuation and phase velocity. J. acoust. Soc. Amer. 69, 696—701.
169. O'Donnell, M., Mimbs, J. W, Sobel, В. E., & Miller, J. G. (1977) Ultrasonic attenuation of myocardial tissue: dependence of time after excision and on temperature. J. acoust. Soc. Amer. 62, 1054—1057.
170. Ophir, J. & Jaeger, P. (1982) Spectral shifts of ultrasonic propagation through media with nonlinearly dispersive attenuation. Ultrasonic Imaging, 4, 282—289.
171. Papadakis, E. P. (1966) Ultrasonic diffraction loss and phase change in anisotropic materials. J. acoust. Soc. Amer. 40, 863—876.
172. Papadakis, E. P. (1970) Effects of input amplitude profile upon diffraction loss and phase change in a pulse-echo system. J. acoust. Soc. Amer., 49, 166—168.
173. Papadakis, E. P. (1973) Ultrasonic diffraction loss and phase change for broad-band pulses, /. acoust. Soc. Amer., 3, 847—849.
174. Papadakis, E. P., Fowler, K. A., & Lynnworth, L. (1973) Ultrasonic attenuation by spectrum analysis of pulses in buffer rods: Methods and diffractions corrections. J. acoust. Soc. Amer. 53, 1336—1343.
175. Parker, K. J. (1983) Ultrasonic attenuation and absorption in liver tissue. Ultrasound Med. Biol. 9, 363—369.
176. Parker, K. J. & Waag, R. C. (1983) Measurement of ultrasonic attenuation within regions selected from B-scan images, IEEE Trans. Biomed. Eng., BME-30, 431—437.
177. Pauly, H. & Schwan, H. P. (1971) Mechanism of absorption of ultrasound in liver tissue. /. acoust. Soc. Amer. 50, 692—699.
178. Pellam, J. R. & Gait, J. K. (1946) Ultrasonic propagation in liquids: I. Application of pulse technique to velocity and absorption measurements at 15 megacycles. J. Chem. Phys. 14, 608—614.
179. Penttinen, A. & Luukkala, M. (1977) Diffraction losses associated with curved ultrasonic transducers. J. Phys. D: Appl. Phys., 10, 665—669.
180. Phillippoff, W. (1963) Viscoelasticity of polymer solutions at high pressures and ultrasonic frequencies. J. Appl. Phys. 34, 1507—1511.
181. Pinkerton, J. M. M. (1947) A pulse method for the measurement of ultrasonic absorption in liquids: results for water. Nature 160, 128—129.
182. Pohlhammer, J. & O'Brien, Jr. W. D. (1981) Dependence of the ultrasonic scatter coefficient on collagen concentration in mammalian tissue. J. acoust. Soc. Amer. 69, 283—285.
183. Pohlhammer, J. D., Edwards, C. A., & O'Brien, Jr. W. D. (1981) Phase insensitive ultrasonic attenuation coefficient determination of fresh bovine liver over an extended frequency range. Med. Phys. 8, 692—694.
184. Pohlman, R. (1939) Uber die Absorption des Ultraschalls im menschlichen Gewebe und ihre Abhangigkeit von der Frequencz. Physik Z. 40, 159—161.
185. Raichel, D. R. (1971) Sound propagation in Voigt fluid. J. acoust. Soc. Amer. 52, 395—398.
186. Redwood, M. (1963) A study of waveforms in the generation and detection of short ultrasonic pulses. Appl. Mat. Res. April 1963, 76—84.
187. Robinson, Т. C. & Lele, P. P. (1972) An analysis of lesion development in the brain and in plastics by high-intensity focused ultrasound at lowmegahertz frequencies. J. acoust. Soc. Amer. 51, 1333—1351.
188. Sadykhova, S. Kh. & Elpiner, I. E. (1970) Absorption of ultrasonic waves in aqueous solutions of biopolymers. Soviet Physics-Acoustics, 16, 101—107.
189. Schwan, H. P. & Carstensen, E. L. (1952) Ultrasonics aids diathermy experiments. Electronics, July '52, 216.
190. Sehgal, С. M. & Greenleaf, J. F. (1982) Ultrasonic absorption and dispersion in biological media: a postulated model. J. acoust. Soc. Amer., 72, 1711—1718.
191. Seki, H., Granato, A., & Truell, R. (1956) Diffraction effects in the ultrasonic field of a piston source and their importance in the accurate measurement of attenuation. /. acoust. Soc. Amer. 28, No. 2, 230—238. 192. Shaffer, S., Pettibone, D. W., Havlice, J. F. & Nassi, M. (1984) Estimation of the
slope of the acoustic attenuation coefficient. Ultrasonic Imaging 6, 126—138. 193. Shung, К. K. & Reid, J. M. (1978) Ultrasonic scattering from tissues, in: 1977 Ultrasonics Symposium Proceedings IEEE Cat. No. 77 CH 1264-159, 230—233.
194. Shung, К. K., Sigelmann, R. A., and Reid, J. M. (1976) Scattering of ultrasound by blood. IEEE Trans. Biomed. Eng., 23, 460—467.
195. Strom-Jensen, P. R. & Dunn, F. (1984) Ultrasonic absorption by solventsolute interactions and proton transfer in aqueous solutions of peptides and small proteins. J. acoust. Soc. Amer. 75, 960—966.
196. Tervola, К. M. U, Foster, S. G., & O'Brien, Jr. W. D. (1985) Attenuation coefficient measurement technique at 100 MHz with the scanning laser acoustic microscope. IEEE Trans. Sonics and Ultrasonics, SU-32, 259—265.
197. Tervola, К. M. U, Grurnmer, M. A., Erdman, Jr. J. W., & O'Brien, Jr. W. D. (1985) Ultrasonic attenuation and velocity properties in rat liver as a function of fat concentration. A study at 100 MHz using a scanning laser acoustic microscope. J. acoust. Soc. Amer. 77, 307—313.
198. Truell, R. & Oates, W. (1963) Effect of lack of parallelism of sample faces on the measurement of ultrasonic attenuation. J. acoust. Soc. Amer. 35, 1382—1386.
199. Truong, X. T. (1972) Extensional wave propagation characteristics in striated muscle. J. acoust. Soc. Amer. 51, 1352—1356.
200. Truong, X. Т., Jarrett, S. R., & Rippel, D. V. (1978) Longitudinal pulse propagation characteristics in striated muscle. J. acoust. Soc. Amer. 64, 1298—1302.
201. Vinson, F. S., Eggleton, R. C, & Meiss, R. A. (1978) Variations in acoustic velocity in skeletal muscle determined by acoustic microscopy. In: Ultrasound in medicine 4, (ed. White, D. N.) Plenum Press, N.Y. 519—534.
202. Wells, P. N. T. (1969) Physical principles of ultrasonic diagnosis. Academic Press, London and New York. j
203. Wells, P. N. T. (1975) Absorption and dispersion of ultrasound in biological tissue. J Ultrasound Med. Biol. 1, 369—376. s
204. Wells, P. N. T. (1977) Biomedical ultrasonics. Academic Press, London. J
205. Wilson, L. S., Robinson, В. E., & Doust, D. B. (1984) Frequency domain processing j for ultrasonic attenuation measurement in liver. Ultrasonic Imaging, 6, j 278—292.
206. Wladimiroff, J. W, Croft, I. L., & Talbert, D. G. (1975) In vitro measurements of sound velocity in human fetal brain tissue. Ultrasound Med. Biol. 1, j 377—382.
207. Woodcock, J. P. (1979) Ultrasonics. Adam Hilger, Bristol.
208. Yosioka, K., Ohmura, A., Hasegawa, Т., &; Oka, M. (1968) Absorption coefficient of ultrasound in soft tissues and their biological conditions. Proc. 6th Interna- j tional Congress on Acoustics, Tokyo, Japan. Paper M-l-3, pp. M-5 to M-8.
209. Yuhas, D. E. & Kessler, L. W. (1979) Acoustic microscope analysis of myocardium.
In: Ultrasonic tissue characterization II. Linzer, M. (ed.), NBS Special Publication 525, U.S. Government Printing Office, Washington, D.C, 73—79.
СКОРОСТЬ ЗВУКА
Дж. Бэмбер
В предыдущих главах были затронуты различные вопросы, связанные со скоростью звука в биологических тканях. В частности, в гл. 4 рассматривались биофизические механизмы поглощения и дисперсии ультразвуковых волн и представлены данные о влиянии экспериментальных условий на результаты измерений скорости звука в биологических тканях. В данной главе основное внимание будет уделено двум вопросам — измерению скорости звука и анализу опубликованных данных.
Здесь уместно напомнить, что, строго говоря, не существует простого и однозначного определения скорости звука. В предыдущих главах мы пользовались понятиями как групповой, так и фазовой скорости звука. Скорость звука зависит от амплитуды колебаний при распространении волн конечной амплитуды. Тем не менее при решении практических задач применения ультразвука в медицине общепринятой является следующая упрощенная трактовка: для любой данной среды существует некоторое единственное значение скорости звука, которое можно измерить.
5.2. Измерение скорости ультразвуковых волн в биологических тканях
Измерение скорости звука не вызывает серьезных затруднений в тех случаях, когда можно ограничиться не очень высокой степенью точности (например, 1%). Трудности будут возникать, если необходимо обеспечить высокую точность абсолютных измерений или малую погрешность относительных измерений скорости. Так, например, те методы и устройства, которые широко используются для исследования биологических тканей, лишь в редких случаях имеют точность, позволяющую измерить дисперсию скорости звука в частотном диапазоне, характерном для медицинских приложений ультразвука. Отметим также, что в данной книге для определения скорости звука используется термин speed of sound, хотя некоторые авторы применяют понятие sound velocity. Никакого принципиального различия между обоими понятиями нет, поэтому, чтобы быть последовательными, мы сохраним первое название, понимая под ним скалярную характеристику исследуемой среды. Вполне возможно, однако, что в тех случаях, когда речь идет о векторной величине, характеризующей скорость и направление распространения акустической энергии или движение частиц среды, предпочтительнее использовать термин sound velocity.
Как уже отмечалось в гл. 4, во многих случаях те методы и аппаратура, которые применяются для измерений затухания ультразвука, пригодны и для измерений скорости звука. Прекрасный анализ различных вопросов, связанных с измерением скорости звука, дан в обзорных работах Бейера и Летчера [9], Данна и др. [26], Госса и др. [37], Мак-Скимина [63] и Матесона [65]. Ранее мы уже ссылались на эти работы при рассмотрении проблемы измерения затухания звука. Кроме того, следует отметить работу Сарвазяна [81], посвященную детальному анализу методов измерения скорости звука в биологических соединениях и исследованию факторов, влияющих на скорость звука. Большей частью те замечания и выводы, которые были сделаны в разд. 4.4.1.2 при рассмотрении конкретных измерительных систем (например, в отношении их рабочего диапазона частот или возможностей применения для измерений в биологических тканях), справедливы и в данном случае. Мы рекомендуем читателям в процессе ознакомления с дальнейшим материалом обращаться также и к разд. 4.4.1.2.
5.2.1.1. Абсолютные измерения
Методы абсолютных измерений обеспечивают возможность непосредственного измерения скорости звука в исследуемой среде и не требуют знания скорости звука в какой-либо эталонной среде. Такие измерения могут проводиться как в импульсном, так и в непрерывном режимах излучения; при этом могут использоваться системы с фиксированным или переменным расстоянием (см. гл. 4).
Принцип действия многих широко применяемых измерительных систем независимо от их модификации основан на измерении времени распространения зондирующего акустического импульса через исследуемую среду. Первоначально этот принцип был использован Пелламом и Галтом [75] в системе с переменным расстоянием, разработанной специально для жидкостей. Скорость звука определялась по разнице во временах распространения импульсов при изменении на заданную величину длины пути между излучающим и приемным преобразователями или же между излучающим преобразователем и плоским отражателем. При известной фиксированной длине пути регистрируемым параметром может быть либо время однократного прохождения импульса, либо суммарное время прохождения многократно переотраженных импульсов между двумя плоскостями (излучателем и приемником или же между излучателем и плоским отражателем). Основное различие между измерительными системами заключается в степени сложности тех аппаратурных решений и алгоритмов, которые применяются для точного определения времени распространения сигнала и введения дифракционных поправок и учета различных погрешностей. Следует, однако, отметить, что даже самые простые измерения времени распространения сигнала с помощью обычного осциллографа позволяют обеспечить погрешность не хуже ±0,5% [62]. При использовании более сложных систем погрешность измерения скорости звука может быть уменьшена до ±0,2%. В методе суперпозиции, предложенном Бейером и Летчером [9], частота повторения ультразвуковых импульсов подбирается таким образом, чтобы следующие друг за другом отраженные эхо-сигналы совмещались. В этом случае время распространения определяется по временному интервалу между импульсами. Пападакис [72] разработал метод оптического наложения эхо-импульсов, реализуемый с помощью осциллографа, временная развертка которого запускается внешним сигналом. Здесь вместо наложения акустических импульсов используется наложение принятых электрических сигналов на экране осциллографа, что достигается путем изменения частоты запуска развертки осциллографа. При этом искомое время распространения вновь определяется по временному интервалу между импульсами запуска. В автоматическом варианте подобной системы, получившей название схемы синхрокольца [41], применялись раздельные излучающий и приемный преобразователи и из принятого импульса формировался сигнал запуска, который по цепи обратной связи вновь подавался на излучающий преобразователь. Тем самым обеспечивалась автоподстройка частоты повторения, что позволяло непосредственно измерить время распространения акустического сигнала в исследуемой среде. В работе [89] подобный метод использовался для измерений скорости звука in vitro в различных биологических жидкостях и опухолях головного мозга. Сообщалось, что в случае однородных сред ошибка измерения скорости звука не превышала 0,1%.
Для определения скорости звука с высокой точностью в частотном диапазоне от 1 до 100 МГц с успехом применяются ультразвуковые интерферометры, работающие в непрерывном режиме излучения (см. разд. 4.4.1.2 в гл. 4). С их помощью сравнительно легко получить погрешность измерений менее ±0,1%, а в принципе точность измерения скорости звука интерферометрическим способом может достигать ±10-4% [82]. Одни из наиболее точных измерений скорости звука в дистиллированной воде были выполнены с помощью интерферометров с переменной базой [21]. С помощью интерферометра с переменной базой удавалось проводить измерения даже в мягких тканях, но для этого в процессе измерения приходилось сжимать образец на 25% [35].
5.2.1.2. Относительные измерения
За редким исключением, рассмотренные выше методы абсолютных измерений непригодны для исследования биологических тканей, что связано либо с трудностями точного определения длины пути прохождения ультразвука в образце, либо с невозможностью изменения этого пути. В связи с этим стали развиваться методы относительных измерений. Этому в значительной мере способствовало опубликование достоверных данных об абсолютных значениях скорости звука в ряде материалов, которые могли использоваться в качестве эталонных сред при проведении сравнительных измерений. Обычно эталонной средой служила дистиллированная вода, иногда применялся также физиологический раствор с известной концентрацией хлорида натрия. В принципе точность относительных измерений определяется той точностью, с которой выполнены измерения в эталонной среде. При использовании в качестве эталона воды эта точность может достигать ±0,03%, однако, как будет показано в разд. 5.2.2, в случае биологических сред результирующая точность измерений в значительно большей степени ограничивается влиянием других факторов.
Для проведения относительных измерений скорости звука в биологических тканях с использованием эталонной среды широко применяются различные модификации рассмотренного ранее импульсного метода регистрации времени распространения акустического сигнала. На практике этот метод реализуется с помощью различных схем измерения с использованием либо одного, либо двух преобразователей [56, 69, 93]. В качестве примера можно привести схему с двумя преобразователями, которая использовалась для исследования затухания звука способом введения образца (см. рис. 4.5). При такой схеме для проведения измерений скорости звука требуется лишь осциллограф с высокой скоростью развертки, обеспечивающей возможность измерения временного сдвига At в местоположении принятого акустического импульса на экране осциллографа после введения исследуемого образца ткани в акустический тракт системы. В большинстве случаев достаточно, чтобы скорость временной развертки составляла 0,1 мкс/см. При известном значении скорости звука ![]() в воде или какой-либо другой используемой эталонной среде искомое значение скорости звука в исследуемом образце ткани
в воде или какой-либо другой используемой эталонной среде искомое значение скорости звука в исследуемом образце ткани ![]() усредненное по пути прохождения акустического пучка в ткани
усредненное по пути прохождения акустического пучка в ткани ![]() , можно рассчитать по следующей формуле:
, можно рассчитать по следующей формуле:
![]()
Фостер и др. [30] использовали подобную методику, но в несколько модифицированном виде (применялся фокусирующий преобразователь и плоский отражатель) для получения макроскопической картины распределения скорости звука совместно с распределениями коэффициентов затухания и обратного рассеяния в тонких срезах удаленной ткани молочной железы. Для получения пространственных распределений скорости звука в срезах ткани in vitro применялись также спектрометрические системы с временной задержкой [45] (см. разд. 4.4.1.2).
В разд. 4.4.1.2 была описана узкополосная система Швана и Карстенсена, позволяющая при измерениях затухания звука в жидкостях свести к минимуму влияние дифракционных эффектов. Эта цель достигалась за счет постоянства пути прохождения акустического сигнала между излучателем и приемником, первый из которых находился в эталонной жидкости, а второй — в исследуемой. При этом изменение длины пути в исследуемой жидкости компенсируется соответствующим изменением длины пути в эталонной жидкости. Системы подобного типа позволяют также проводить прецизионные измерения фазовой скорости звука (фактически результирующая точность нахождения скорости в данном случае будет определяться той точностью, с которой известна скорость звука
в эталонной жидкости) и исследовать дисперсию скорости в жидких средах. С этой целью сигнал приемного преобразователя смешивается с электрическим опорным сигналом, возбуждающим излучатель, что позволяет найти фазовый сдвиг между этими сигналами при изменении длины пути акустического импульса в образце [14].
5.2.1.3. Акустическая микроскопия
Довольно часто возникает необходимость в проведении измерений скорости звука в микроскопическом масштабе, т. е. с очень высоким пространственным разрешением. Подобные задачи приходится решать, например, в тех случаях, когда исследуемое вещество имеется лишь в малом количестве или же требуется получить микроскопическую картину распределения скорости звука (и плотности), которая позволила бы проанализировать характер рассеяния ультразвуковых волн в данном образце на макроскопическом уровне (см. гл. 6).
В работе [29] рассмотрено применение растрового лазерного акустического микроскопа (РЛАМ) для измерений пространственных распределений скорости звука в образцах биологических тканей толщиной 300—900 мкм на частоте 100 МГц. Поле зрения такого микроскопа составляло 3x2 мм2. В случае однородных сред подобный акустический микроскоп обеспечивает чувствительность измерений около ±0,3%, но дает завышенные абсолютные значения (не более чем на 2%). В РЛАМе формирование трансмиссионных акустических (модулированных по затуханию звука) изображений образца осуществляется с помощью сканирующей лазерной системы, воспроизводящей микромасштабное пространственное распределение амплитуды смещения нижней поверхности зеркального покровного стекла, установленного над исследуемым образцом. Акустическая волна, падающая наклонно на образец снизу, проходит через него и вызывает деформацию поверхности отражателя, которая считывается лазерным лучом.
В другом режиме работы РЛАМа выходной сигнал приемника лазерного излучения смешивается с электрическим опорным сигналом частотой 100 МГц. В результате формируется интерференционная картина, состоящая из светлых и темных полос. В случае однородных сред эти полосы имеют вид прямых линий и отстоят друг от друга на одинаковое расстояние. На первом этапе исследования получают интерференционную картину, пропуская акустический пучок, например, через физиологический раствор известной концентрации. Затем после введения в этот раствор тонкого среза исследуемой ткани анализируют изменения, появляющиеся в интерференционной картине. Определяя направление и величину смещения каких-либо полос, по известной скорости звука в физиологическом растворе можно рассчитать значение скорости звука в заданной точке образца ткани.
Грант и Бернадин [38] использовали интерферометрический режим работы РЛАМа для измерений скорости звука в очень малых объемах жидкостей (около 0,05 мл). С этой целью к торцу зеркального отражателя прикреплялась специальная прокладка, образующая совместно с отражателем интерферометрическую ячейку клиновидной формы. Исследовалась зависимость скорости звука от концентрации белков в растворах сывороточного альбумина коровы. Сообщалось, что точность определения скорости была лучше ±0,2%, хотя каких-либо конкретных значений ошибки измерений не приводилось.
Помимо РЛАМа для измерений скорости звука в интерферомет-рическом режиме используются также растровые акустические микроскопы (РАМ). Принцип их действия аналогичен принципу действия РЛАМа, зд. исключением того, что вместо лазерного считывания в них применяется механическое сканирование фокусированным приемником ультразвука [19]. Следует отметить, что при работе с РАМом серьезной проблемой является необходимость из, готовления тонких образцов с точно выверенной и одинаковой по всей площади толщиной. В случае РЛАМа такая проблема не возникает, поскольку равномерность толщины образца биологической ткани обеспечивается без каких-либо специальных мер просто за счет его прижима к оправке держателя образца под действием веса зеркального отражателя. Для преодоления подобных трудностей в случае применения РАМа Синклер и др. [85] разработали специальную методику, позволяющую в заданной точке образца измерить критический угол падения излучения из эталонной среды с более низкой скоростью звука в образец ткани (критический угол представляет собой угол падения, при котором возникает полное внутреннее отражение). Зная этот угол, на основе закона Снелля можно определить скорость звука в исследуемой ткани, причем полученное значение, как полагают, практически не будет зависеть от толщины образца. Более подробно РЛАМ и РАМ рассматриваются в разд. 9.7.
5.2.1.4. Измерения in vivo
До недавнего времени основная цель измерения скорости звука в биологических тканях в плане медицинских приложений сводилась к получению данных, позволяющих провести градуировку эхогра-фических систем визуализации по координатам «время распространения — дальность». В настоящее время многие исследователи пришли к выводу, что скорость звука сама по себе является весьма информативной специфической характеристикой ткани. Это послужило толчком для разработки большого числа методов, позволяющих проводить измерения скорости звука и даже получать картину ее пространственного распределения непосредственно в человеческом организме.
Измерения скорости звука в трансмиссионном режиме проводились на различных участках и органах человеческого тела, доступных для исследования. Естественно, что подобные измерения позволяли получать оценки скорости, усредненной по всем тканям, лежащим на пути прохождения ультразвукового пучка. В частности, Коссофф и др. [56] использовали рассмотренный выше метод регистрации времени распространения акустического импульса для относительных измерений усредненной скорости звука в молочной железе. В работах [13, 33, 39, 55] дается дальнейшее развитие этого метода, позволяющее на основе сканирования ультразвуковым пучком по множеству различных направлений получать реконструктивные томографические изображения распределений скорости звука в различных сечениях молочной железы. Подобные томограммы скорости звука, по-видимому, могут служить источником новой информации, дополняющей данные, полученные путем обычной эхографической визуализации. С помощью метода синхрокольца проводилось также исследование in vivo зависимости скорости звука в мышечной ткани бицепса человека от его сократительной способности [68].
Для тех случаев, когда особенно трудно провести прямые измерения в трансмиссионном режиме (например, в печени человека), исследовались возможности определения усредненной скорости звука на основе регистрации акустических эхо-сигналов, отраженных от самой ткани. По-видимому, Робинсон и др. [78] одними из первых предложили использовать для этих целей способ, основанный на определении местоположения и визуализации какого-либо характерного объекта (например, кровеносного сосуда), локализованного в исследуемой ткани. При этом формировалось два изображения выбранного объекта, соответствующие двум различным направлениям распространения эхо-сигналов через контактную среду (воду). Из-за различия скоростей звука в воде и ткани, а также из-за различия углов падения ультразвукового импульса на границу раздела между водой и тканью в обоих случаях два полученных изображения объекта были немного смещены относительно друг друга. Измеряя величину этого смещения и определяя углы падения, с помощью закона преломления Снелля можно рассчитать значение скорости звука в исследуемой ткани, усредненное по эквивалентной длине пути обоих изображений. Воспроизводимость результатов, полученных таким способом in vivo, составляла приблизительно 1%.
Рассмотренный метод использовался в работах [22, 64] для измерений скорости звука в нормальной и пораженной циррозом печени, а также в селезенке. Бэмбер и Эббот [4] предложили несколько модифицированную схему, работающую в сочетании со стандартной линейно сканирующей системой для получения изображений в реальном времени. В этой схеме два смещенных изображения получались за счет введения между поверхностью линейного многоэлементного датчика и тканью акустической бипризмы с известными свойствами и конфигурацией.
Был предложен также метод пересекающихся пучков [1, 42, 46], в основе которого лежит статистическая оценка времени распространения импульса по определенному пути с учетом рассеяния от той области исследуемой ткани, где перекрываются акустические пучки излучателя и приемника, имеющих острые диаграммы направленности. По оценкам на однородных фантомах точность определения скорости после усреднения по 100 импульсам может достигать ±0,5%.
Необходимо упомянуть еще два метода, позволяющие провести оценку средней скорости звука путем наблюдения характера фокусировки при получении эхо-импульсных изображений тканей с помощью акустических систем с широкой апертурой, т. е. с высоким разрешением. В методе, предложенном Хайяши и др. [44], для получения изображения в реальном времени использовалась специально модифицированное сканирующее устройство, обеспечивающее возможность ручного управления цифровыми линиями задержки, с помощью которых формируются фокусированный ультразвуковой пучок и требуемая диаграмма направленности приемника. После соответствующей градуировки усредненное значение скорости звука в биологической ткани рассчитывается на основе данных о временах задержки, при которых получается наиболее резкое изображение. Резкость изображения оценивается путем визуального наблюдения. Применительно к однородным средам расчетная точность определения скорости звука составляет ±0,5%. Во втором методе, который реализуется с помощью более сложной системы фокусировки, заложена возможность получения распределений скорости звука in vivo на основе обработки принятых эхо-сигналов. Несмотря на известную сложность реализации, такая возможность делает подобный подход, по-видимому, наиболее универсальным из всех существующих. Для автоматической оценки резкости изображений, получаемых посредством вариаций предполагаемых значений скорости звука на этапе реконструкции по методу синтезированной апертуры, применяется критерий минимума энтропии [66].
5.2.2. ПРОБЛЕМЫ, АРТЕФАКТЫ И ПОГРЕШНОСТИ
5.2.2.1. Погрешности измерений в образцах однородных тканей
А. Оценка длины акустического пути. Как и при измерениях затухания звука, результирующие точность и погрешность определения скорости звука в образцах биологических тканей в существенной степени зависят от правильности определения длины акустического пути в исследуемом образце. Довольно часто точное определение длины пути при использовании методов относительных измерений, описываемых, например, уравнением (5.1), вызывает большие трудности. Однако достоинство методов относительных измерений именно в том и заключается, что, даже при погрешностях измерения длины пути, достигающих ±10%, ошибка определения скорости звука не превысит ±1%, если в качестве эталонной среды используется вода или физиологический раствор.
Б. Скорость звука в эталонной среде. Сравнительно высокая точность методов относительных измерений скорости звука обусловлена тем, что в литературе приводятся достоверные значения скорости звука для ряда сред, которые можно использовать в качестве эталонных жидкостей. При этом весьма желательно располагать информацией о соответствующей температуре и степени чистоты эталонной среды. Если в качестве такой среды используется вода, то для целей контроля за температурой достаточно использовать стандартный лабораторный ртутный термометр. В этом случае погрешность определения скорости звука, связанная с погрешностью таких термометров, вряд ли будет превышать ±0,4% при 20°С.
В. Регистрация времени прихода сигнала. Ранее считалось, что метод измерения времени распространения акустического сигнала представляет собой простой, но достаточно точный метод определения скорости звука. Однако этому методу присущ один существенный недостаток. Он заключается в том, что для определения времени прихода импульса необходимо «привязаться» к некоторой реперной точке на его профиле или же воспользоваться каким-либо другим критерием. Выбор единственной реперной точки не всегда приемлем, поскольку форма излучаемого импульса может меняться по мере распространения через исследуемую среду. Такое изменение может иметь место как в однородных, так и в неоднородных средах в тех случаях, когда среда характеризуется дисперсией скорости звука или частотной зависимостью коэффициента затухания (мы пренебрегаем случаем нелинейного распространения). Следует отметить, что в биологических тканях дисперсия скорости звука сама по себе весьма незначительна и не приводит к заметному искажению формы импульса. В свою очередь это означает, что импульсную методику измерения сигнала трудно использовать для исследования дисперсии скорости в подобных средах. В противоположность этому затухание ультразвука в тканях сильно зависит от частоты. Как отмечал Редвуд [77], преимущественное затухание высокочастотных составляющих в спектре импульса будет приводить по мере его распространения к все более заметному его уширению. На рис. 5.1 показано, как изменяется форма импульса с несущей частотой 10 МГц после прохождения 5 см пути в среде, коэффициент затухания которой линейно зависит от частоты и имеет значение 1 дБ/(см • МГц). Этот простой пример, полученный путем математического моделирования прохождения импульса через частотный фильтр (без сдвига фазы), наглядно показывает, что погрешности за счет уширения импульса будут минимальными, если в качестве реперной точки выбрать центр импульса. Однако в тех случаях, когда форма импульса заметно меняется, местонахождение центра импульса определить достаточно трудно. Поэтому часто выбираются другие реперные точки, особенно если возникает необходимость в автоматизации метода измерения. Так, например, Гринлиф и др. [40] при измерении времени распространения импульса в качестве реперной точки использовали тот первый момент времени, когда на фоне шума появляется полезный сигнал. Боуэн и др. [11] регистрировали момент времени, когда сигнал впервые пересекает нулевую отметку. Однако и эти критерии не являются идеальными. В частности, их применение в случае, показанном на рис. 5.1, приводит к заниженным оценкам времени распространения импульса, причем погрешности, выраженные в длинах волн, составляют соответственно 0,5![]() и 0,6
и 0,6![]() .
.
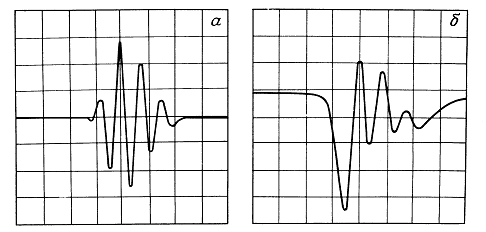
Рис. 5.1. Уширение импульса под влиянием дисперсии затухания, рассчитанное с помощью компьютерного моделирования. Зависимость коэффициента затухания от частоты моделировалась введением частотного фильтра с характеристикой ![]() /f = = 1 дБ/(см • МГц), а — форма исходного импульса с центральной частотой 10 МГц; б — тот же импульс после прохождения расстояния 5 см в среде с указанным затуханием. Оба импульса синтезировались с помощью цифро-аналогового преобразователя и воспроизводились на экране осциллографа с произвольным вертикальным усилением.
/f = = 1 дБ/(см • МГц), а — форма исходного импульса с центральной частотой 10 МГц; б — тот же импульс после прохождения расстояния 5 см в среде с указанным затуханием. Оба импульса синтезировались с помощью цифро-аналогового преобразователя и воспроизводились на экране осциллографа с произвольным вертикальным усилением.
С другой стороны, применение критерия Гринлифа и др. позволяет уменьшить число других артефактов, которые возникают при реконструкции времени распространения импульса. Если длина акустического пути через исследуемый образец составляет 4—5 см, то в случае экспериментальной схемы, описываемой уравнением (5.1), применение в качестве реперной точки начального момента появления сигнала приводит к получению завышенных значений скорости звука приблизительно на 4%. Следует подчеркнуть, что величина этой погрешности в значительной мере зависит от того, насколько точно определено значение наклона частотной зависимости коэффициента затухания в пределах рассматриваемой длины пути ультразвукового сигнала. Более подробно этот вбпрос обсуждается в разд. 5.2.2.2.
Г. Дифракционные поправки. При измерениях скорости звука необходимо вводить поправки на дифракционные фазовые искажения, аналогичные по своей природе дифракционным искажениям, возникающим при измерениях затухания. Расчет таких поправок применительно к измерительным системам с переменным расстоянием был выполнен Пападакисом [73]. Оценки дифракционных поправок для случая плоского круглого преобразователя можно найти в работе [84] (см. рис. 4.6), а в работе [90] представлены результаты аналогичных расчетов для фокусирующих преобразователей. Было показано, что при использовании методов оптического наложения и суперпозиции импульсов погрешности, связанные с дифракционными фазовыми искажениями, могут достигать значения 0,25 от периода высокочастотного заполнения импульса [74]. В случае применения метода введения образца фазовыми искажениями за счет дифракции обычно пренебрегают.
В интерферометрических системах влияние дифракции на точность измерения скорости звука становится заметным на частотах ниже 3 МГц. Обзор работ, посвященных анализу этого влияния, приведен в [87], где также показано, что в использованной авторами системе дифракционные искажения более чем в 3 раза превышали соответствующие расчетные значения. В частности, было получено, что дифракционные искажения приводят к завышенным значениям скорости звука, которые могут отличаться от реальных значений на 0,5%.
Д. Влияние конструктивных особенностей преобразователей на точность определения времени распространения и длины пути акустического сигнала. В работе [53] показано, что при измерениях времени однократного прохождения импульса в схемах с фиксированным расстоянием необходимо делать поправку на четвертьволновые, согласующие по импедансу или изолирующие слои. При определении времени поступления импульса необходимо также учитывать погрешности, возникающие из-за внутренних переотражений сигнала на приемном преобразователе. Применение дифференциальных схем измерения позволяет решить как эту проблему, так и проблему, связанную с изменением фазы сигнала в результате отражения от мишени [9].
Для измерений скорости звука нецелесообразно применять преобразователи с большой апертурой или сильно фокусирующие преобразователи, поскольку при их использовании нельзя точно определить, какого конкретно участка поверхности преобразователя вначале достигнет ультразвуковая волна. Это в свою очередь может привести к неоднозначности в определении длины пути.
5.2.2.2. Влияние неоднородностей на время прихода сигнала
В гл. 4 было показано, что эффекты компенсации фаз могут приводить к существенным погрешностям при измерениях затухания звука. По-видимому, подобные эффекты в равной мере могут быть причиной значительных погрешностей и при измерениях времени распространения импульса. Это обусловлено тем, что наиболее заметные изменения формы акустического импульса могут быть связаны именно с действием этих эффектов. Отсюда также следует, что в качестве реперной точки предпочтительнее выбрать момент первого появления сигнала, а не те моменты времени, где амплитуда сигнала достигает максимума [76] или же проходит через нулевую отметку [11, 57].
В работе [61] представлены результаты статистического анализа времени прихода на приемник электромагнитных и световых импульсов, распространяющихся в турбулентной и сильно рассеивающей среде. Было показано, что в таких средах возникает дополнительное запаздывание во времени прихода сигнала, связанное главным образом с наблюдаемым уширением импульса, а не с его угловыми отклонениями. В этом случае временной «центр масс» импульса, определяемый первым статистическим моментом сигнала, испытывает существенно меньшие флуктуации по сравнению с дополнительным временным запаздыванием импульса, вызванным его уширением. По аналогии можно предположить, что использование критерия «центра масс» может дать определенные преимущества и при оценке времени прихода акустического сигнала. На практике применить такой критерий можно с помощью квадратичного детектирования высокочастотного импульса. Следует также отметить, что Чиневерт и др. [17] добились заметного повышения точности реконструкции пространственных распределений скорости звука за счет применения специального устройства оценки времени распространения импульса. В этом устройстве осуществлялась операция кросс-корреляции принятых сигналов с опорным сигналом, для которого время распространения известно.
Подобный подход может быть применен не только во временной, но также и в спектральной области. В частности, он использовался при проведении относительных измерений методом замещения. При этом фазовый спектр принятого акустического импульса (полученный посредством оцифровки импульса с последующей операцией фурье-преобразования) вычитался из фазового спектра импульса, прошедшего через эталонную среду. Полученный в результате такой операции «разностный» фазовый спектр может быть использован для расчета фазовой и групповой скорости звука. Следует отметить, что существует несколько различных методик такого расчета. Кроме того, разработан метод оценки поправочных коэффициентов для фазовой скорости на фиксированной частоте, введение которых может стать необходимым при наличии в среде заметной дисперсии скорости [90]. Согласно этому методу, скорректированное значение фазовой скорости определяется на основе предположительной оценки величины дисперсии, которая в свою очередь рассчитывается с помощью уравнения (4.42), описывающего взаимосвязь между дисперсией скорости и частотной зависимостью затухания.
5.2.2.3. Испытания на стандартных материалах
Ввиду отсутствия некоторого общепринятого стандарта проверку погрешности какой-либо измерительной системы можно осуществить, выполняя измерения на таких материалах, параметры которых уже исследованы и результаты измерений для которых хорошо воспроизводятся. Наиболее широко для контрольных измерений скорости звука используется дистиллированная вода, иногда для этих целей применяется также физиологический раствор с известной концентрацией хлорида натрия. При проведении подобных измерений необходим строгий контроль за температурой среды. С другой стороны, контролируемое изменение температуры может служить удобным средством испытания измерительной системы в определенном диапазоне значений скорости звука. На рис. 5.2 представлены зависимости скорости звука от температуры для дистиллированной воды, физиологического раствора и различных смесей этилового спирта с водой. Дель-Гроссо и Мейдер [21] на основании обработки экспериментальных данных получили, что зависимость скорости звука в дистиллированной воде от температуры хорошо аппроксимируется полиномом пятой степени. Было показано, что такая аппроксимация позволяет рассчитать скорость звука в воде с точностью не хуже 0,015 м/с при нормальном атмосферном давлении в интервале температур (Г) от 0 до 100°С. Соответствующее выражение, которое использовалось при построении показанной на рис. 5.2 температурной зависимости скорости звука в воде, имеет вид

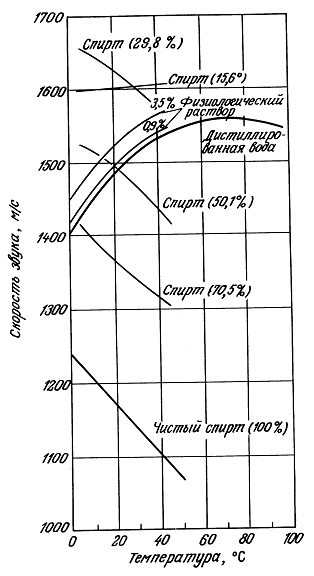
Рис. 5.2. Зависимость скорости звука от температуры в средах, которые использовались при измерениях в качестве эталонных сред. Эти же среды применялись при оценках погрешностей измерительной аппаратуры. Представленные данные заимствованы из работ [21] (вода), [20] (физиологический раствор), [32] (смеси этилового спирта с водой).
Указанные процентные концентрации физиологического раствора соответствуют граммам сухой соли на 100 см3 воды; процентные концентрации спирта соответствуют весовой концентрации этилового спирта в воде. Все данные получены при гидростатическом давлении в 1 атм.
где коэффициенты ki имеют следующие значения:
|
i |
Ki (м/с) |
|
|
0 |
1402,38754 |
|
|
1 |
5,03711129 |
|
|
2 |
-5,80852166• 10-2 |
|
|
3 |
3,34198834•10-4 |
|
|
4 |
-1,47800417•10-6 |
|
|
5 |
3,14643091• 10-9 |
|
Большая часть данных о скорости звука в водных растворах солей появилась из-за интереса к вопросам гидроакустики и распространения звука в море. Эти данные можно использовать в качестве эталонных величин при лабораторных измерениях скорости звука cs в растворах хлористого натрия. В работе [67] составлены таблицы, характеризующие зависимость скорости звука от солености и температуры воды при атмосферном давлении, а в работе [20] приведены простые эмпирические соотношения, позволяющие рассчитать скорость звука в зависимости от температуры, концентрации поваренной соли и глубины от поверхности воды. При атмосферном давлении (нулевой глубине) соответствующее выражение приводится к виду [52]
![]()
где Т' = Т/10 (Т выражена в градусах Цельсия) и S — концентрация соли в граммах сухого веса на 100 см3 воды.
При контрольных измерениях широкий интервал значений скорости звука можно получить, используя смеси этилового спирта и воды в различных пропорциях. Как видно из рис. 5.2, чистый спирт характеризуется низкими значениями скорости звука и отрицательным температурным коэффициентом скорости. По мере добавления к спирту воды скорость звука в смеси возрастает, а ее температурный коэффициент уменьшается. В конце концов скорость звука достигает максимального значения, превышающего скорость звука в дистиллированной воде, а температурный коэффициент скорости меняет знак. Примечательно, что при концентрации этилового спирта в воде, равной 17% (по весу), температурный коэффициент скорости обращается в нуль. Именно этот факт побудил в свое время Джакомини [32] рассматривать подобную смесь как весьма удобную эталонную среду для исследования скорости распространения акустических волн.
5.2.2.4. Влияние условий измерения
Основные трудности, возникающие при проведении прецизионных измерений или при сравнении данных различных авторов по скорости звука в биологических тканях, связаны с большим разнообразием тех условий, при которых выполнялись те или иные измерения. Так, например, полученные результаты различаются при проведении измерений на образцах ткани и на тканях in vivo. Кроме того, они существенно зависят от времени после смерти, условий хранения образцов и температуры. Мы отсылаем читателя к разд. 4.4.2.5, где кратко изложены полученные к настоящему времени данные о влиянии условий эксперимента на результаты измерения скорости звука, а также затухания и рассеяния звуковых волн.
5.3. АНАЛИЗ ОПУБЛИКОВАННЫХ ДАННЫХ О СКОРОСТИ ЗВУКА
На рис. 5.3 указаны типичные пределы вариаций скорости звука для ряда биологических тканей как человека, так и млекопитающих. Приведенные значения соответствуют экспериментальным данным различных авторов. Для сравнения указаны также значения скорости звука для некоторых материалов небиологического характера. Представленные данные свидетельствуют об отсутствии заметных различий в значениях скорости звука для какой-либо конкретной ткани животных различного вида. Однако подобный вывод нельзя считать окончательно установленным, поскольку явная нехватка данных и отсутствие надлежащего контроля за условиями проведения измерений могут помешать выявлению межвидовых различий при сравнительном анализе. Окончательное решение этого вопроса требует проведения специальных исследований. Как будет показано в следующем разделе, в значительной степени разброс значений скорости звука, измеренных для ткани какого-либо конкретного типа, может объясняться, например, различием температур при проведении измерений.
В целом на основе данных, показанных на рис. 5.3, можно выделить три класса тканей: ткани легкого, малая скорость звука в которых определяется высоким газосодержанием, костную ткань, близкую по своим свойствам к твердому телу, и все остальные жидкие среды и мягкие (водоподобные) ткани организма. Большое различие в скоростях звука и плотностях между мягкими тканями и костями или между мягкими тканями и легкими приводит к очень сильному рассеянию ультразвука на границах раздела между этими тканями. Эти особенности в сочетании с соответственно высокими значениями коэффициентов затухания (см. гл. 4) в тканях первых двух классов чрезвычайно затрудняют, а зачастую делают просто невозможным получение качественных акустических изображений структур, расположенных за легкими (или другими газосодержащими областями) и костями. В тканях, относящихся к третьему классу (т. е. в биологических жидкостях и мягких тканях), различия в скорости звука невелики. Максимальные отклонения от некоторого среднего значения составляют для этих тканей всего лишь ±10%. Поэтому при разработке систем акустической визуализации, предназначенных для получения изображений различных структур человеческого организма, часто в общем-то обоснованно используется допущение о постоянстве скорости звука во всех этих структурах. Такое допущение позволяет с определенной точностью рассчитать глубину залегания исследуемой структуры по времени прихода отраженного сигнала. По-видимому, лишь одна группа исследователей придерживается другого мнения на этот счет. А именно, Джеллинс и Коссофф [47] считают, что до анализа акустических изображений определенную калибровку по средней скорости ультразвука необходимо проводить для каждого пациента индивидуально. По их мнению, такая необходимость вызвана главным образом тем, что неправильный выбор предполагаемого значения скорости звука будет приводить к пространственному смещению составных изображений и как следствие к размытию результирующей картины при использовании сложного сканирования (см. разд. 8.4). Аналогичным образом при отсутствии точных данных о скорости звука размытое изображение будет получаться и в случае применения широкоапертурных систем, в которых динамическая фокусировка осуществляется с помощью электронного управления многоэлементной матрицей приемных преобразователей.
Из рис. 5.3 следует также, что значения скорости звука в большинстве биологических жидкостей и мягких тканей (за исключением жировой ткани, характеризующейся наименьшим значением скорости звука в этом классе) превышают скорость звука в воде, причем наибольшая скорость наблюдается в мышечных сухожилиях.
Сами мышцы интересны в том плане, что они характеризуются анизотропией структуры и способностью к сокращению. До сих пор существуют различные мнения относительно того, когда скорость звука будет больше — при распространении акустической волны поперек или вдоль мышечных волокон. Людвиг [62] нашел, что скорость звука в языке коровы практически не зависела от ориентации образца относительно ультразвукового пучка. Голдмен и Ричарде [35], исследуя скелетные мышцы собаки и кролика, получили, что в этих тканях скорость звука была больше в направлении, перпендикулярном волокнам, тогда как результаты измерений, проведенных Молом и Бредделсом [68] на мышцах различного типа, показали, что скорость звука больше в направлении, параллельном мышечным волокнам.
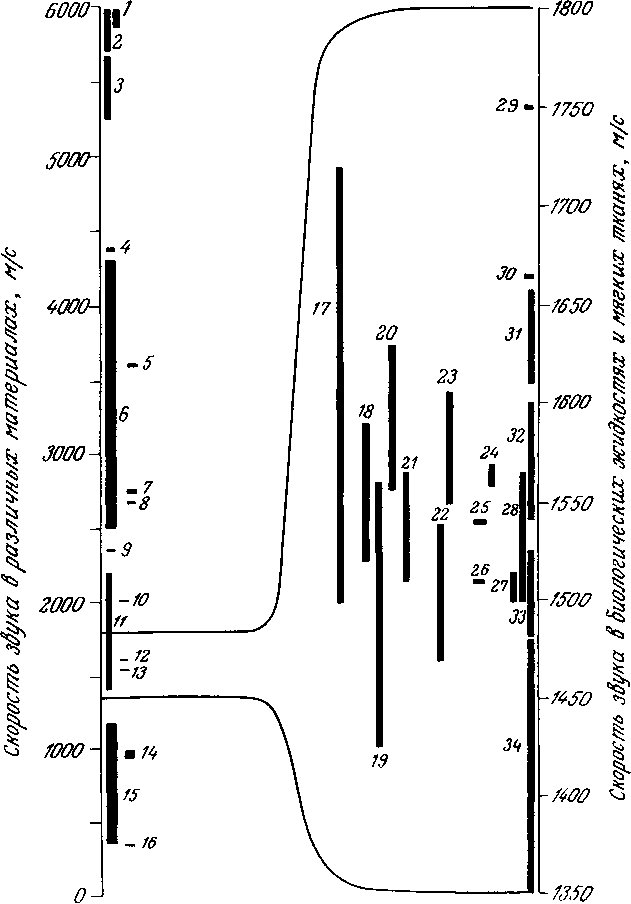
Кроме того, сокращение приводило к росту скорости в мышечной ткани человеческого бицепса при измерениях in vivo [68] и либо к незначительному уменьшению [10], либо к отсутствию изменения скорости звука [68] в мышечной ткани лягушки при измерениях in vitro. Высказывалось предположение, что рост скорости при измерениях in vivo обусловлен изменением кровенаполнения при сокращении мышцы. Следует отметить, что значение скорости звука в некоторых биологических жидкостях человеческого организма можно использовать как определенный диагностический параметр. В частности, в работе Клемина с соавт. [54] сообщалось о заметном расхождении значений скорости звука в желудочном соке, взятом у разных пациентов с различными патологиями (исследовались больные гастритом, язвенной болезнью и раком желудка). Авторы этой работы связывали наблюдаемые вариации скорости с изменением концентрации белков и полипептидов.
Как уже отмечалось, скорость звука в мягких тканях слабо зависит от частоты. Поэтому специально для исследования дисперсии скорости было разработано несколько систем, обеспечивающих высокую точность измерения скорости звука. В качестве примера на рис. 5.4 представлены экспериментально полученные зависимости,
Рис. 5.3. Диапазоны изменения скорости звука в различных биологических средах. Слева представлены соответствующие данные для ряда сред небиологического характера (одни из них включены для сравнения, другие — из-за их использования в научно-исследовательских лабораториях ультразвука). Значения скорости звука в мягких тканях и биологических жидкостях, лежащие в сравнительно узком интервале, показаны с увеличением масштаба на диаграмме справа. Ряд данных получен на тканях, взятых у млекопитающих разного биологического вида; измерения проводились в диапазоне частот 1—10 МГц, температура колебалась в интервале от 20 до 37°С. Все измерения были выполнены либо in vivo, либо на свежеудаленных образцах тканей. 1 — сталь [50]; 2 — кварц [50]; 3 — стекло [50]; 4 — латунь [50]; 5 — зубы [36]; 6 — костная ткань [33, 8, 91, 49, 35]; 7 — плексиглас [78, 50]; 8 — нейлон [50]; 9 — полистирол [50]; 10 — полиэтилен [50]; 11 — желчный камень [36]; 12 — натуральный каучук [50]; 13 — желатин (10%) [27]; 14 — силиконовый каучук марки RTV [27, 28]; 15 — легкие [24, 22]; 16 — сухой воздух [49, 51]; 17 — кожа [35]; 18 — селезенка [48]; 19 — молочная железа [55, 2, 38]; 20— мышечная ткань [35, 17, 67]; 21 — мозг [35]; 22 — стекловидное тело и влага передней камеры; 23 — печень [35, 48]; 24 — почки [35, 48]; 25 — молоко [56]; 26 — околоплодная жидкость [35, 48]; 27—спинно-мозговая жидкость [48]; 28 — физиологический раствор (см. рис. 5.2); 29— сухожилия [35, 48]; 50 — хрящи [35, 48]; 31 — хрусталик глаза [35, 17, 87]; 32 — кровь [35]; 33 — вода (см. рис. 5.2); 34 — жировая ткань [2, 39, 35, 48].
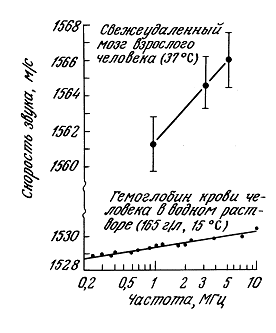
Рис. 5.4. Дисперсия скорости продольных ультразвуковых волн в растворе гемоглобина крови человека [15] и в мозге человека [57]. Данные о дисперсии скорости в костных структурах приведены в тексте (разд. 5.3.1).
характеризующие дисперсию скорости в растворе гемоглобина и мозге человека. Соответствующие расчеты, выполненные в рамках релаксационной теории (см. (4.13)) с использованием общих соотношений между затуханием и дисперсией ультразвука (4.42), показали, что эти экспериментальные данные хорошо согласуются с расчетной величиной дисперсии скорости [57]. Фриззелл и Гиндорф [31] в результате анализа усредненных данных, полученных при исследованиях печени овцы и кошки с помощью РЛАМа, пришли к заключению, что значения скорости звука на частоте 100 МГц и на частотах порядка нескольких мегагерц различаются очень мало.
Помимо высокой скорости звука и сильного затухания (см. разд. 4.5.2.2 и 4.4.3.7) костные ткани характеризуются также и сравнительно сильной дисперсией. В работах [8, 92] высказывалось предположение, что большая величина дисперсии в костях обусловлена главным образом рассеянием ультразвуковых волн. Из-за такой дисперсии при анализе распространения ультразвука в костях необходимо учитывать различие между групповой и фазовой скоростями звука. Костные структуры могут обладать и сильной анизотропией. В частности, в зависимости от типа кости и направления распространения волны величина дисперсии скорости продольных волн может меняться от 1 до 12% в частотном диапазоне 1— 3 МГц. Для сравнения отметим, что дисперсия скорости в мозге в том же частотном диапазоне не превышает 0,2% (рис. 5.4). Помимо продольных в костной ткани могут распространяться и сдвиговые волны. Скорость этих волн также зависит от направления, однако ее величина, изменяющаяся от 1800 до 2200 м/с, всегда остается меньше значения скорости соответствующей продольной волны. Дисперсия сдвиговых волн сравнительно слабо зависит от направления.
5.3.2. ЗАВИСИМОСТЬ СКОРОСТИ ЗВУКА ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
В разд. 4.3.5 уже обсуждалась зависимость скорости звука в воде и разбавленных водных растворах от температуры. Соответствующие кривые, показанные на рис. 5.2, имеют форму параболы. Другой характер имеют температурные зависимости скорости звука в мягких тканях (рис. 5.5). В частности, видно, что жировая ткань отличается от остальных тканей не только низкими значениями скорости звука, но и тем, что температурный коэффициент скорости {Ас/AT) у нее отрицателен. Исследования на тканях нежирового характера показали, что все они характеризуются положительными значениями Ас/AT Отсюда следует, что в сложных структурах типа паренхимы молочной железы [2] зависимость скорости звука от частоты носит непредсказуемый и изменчивый характер. Можно ожидать, что рассеяние ультразвуковых волн на границах раздела между жировой и нежировой тканью будет в сильной степени зависеть от температуры. Все эти эффекты могут найти и полезное практическое применение, поскольку целенаправленное изменение температуры может сделать более эффективным процесс характе-ризации тканей, основанный на измерениях скорости, затухания или рассеяния ультразвука. В работе [48] на основе анализа данных о скорости звука в жировой ткани молочной железы было высказано предположение, что при температурах около 35°С в этой ткани имеет место фазовый переход твердое вещество — жидкость (рис. 5.5). Кремкау и др. [57] наблюдали, что скорость звука в мозге взрослого человека достигает минимума при температуре 15°С. При исследовании мозга ребенка подобного поведения не наблюдалось. Авторы этой работы пришли к выводу, что полученный эффект может быть обусловлен сравнительно высоким содержанием липидов в мозге взрослого человека. При низких температурах температурный коэффициент скорости Ас/AT определяется в основном вкладом липидов, тогда как при повышении температуры основную роль начинают играть компоненты ткани нежирового характера. Результаты, полученные для мозга плода [91] с характерным высоким содержанием воды, показывают, что зависимость скорости звука от температуры в этом случае имеет вид, типичный для тканей нежировой природы.
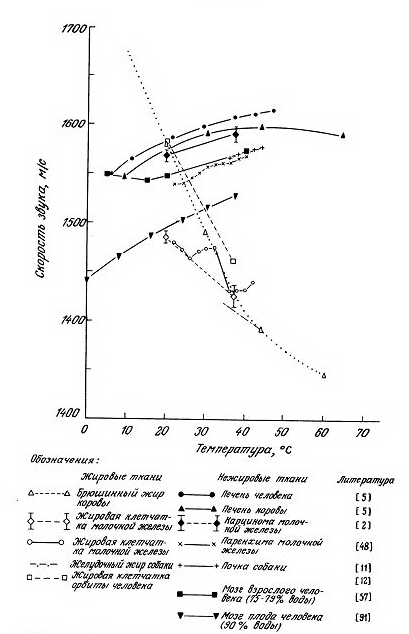
Примечание: вepтикальные чepточки обозначают среднеквадратичное отклонение
Рис. 5.5. Примеры, характеризующие зависимость скорости звука в мягких тканях млекопитающих и человека от температуры. Незакрашенные значки относятся к жировым тканям, закрашенные — к тканям других типов.
Ранее определенные надежды возлагались на использование температурных зависимостей скорости звука для бесконтактного измерения температуры и ее пространственного распределения с целью контроля и регулировки дозы микроволнового или ультразвукового облучения при локальной гипертермии [48]. К сожалению, области медицинского применения современных методов измерения распределения скоростей звука ограничены по существу такими органами, как молочная железа. Кроме того, большие трудности возникают из-за того, что при фиксированной температуре скорость звука может существенно меняться при переходе от одной ткани к другой и даже от образца к образцу ткани одного типа. В ряде работ [11, 16, 69] высказывалась идея о том, что для указанный целей лучше использовать зависимость коэффициента dc/dT от температуры, особенно в тех случаях, когда имеются априорные сведения о пространственном расположении тканей различного типа и данные об изменениях скорости звука и затухания в исследуемой области [43].
Вид зависимостей скорости звука от температуры для мягких тканей нежировой природы с характерным максимумом скорости в области 40—50°С аналогичен подобным зависимостям, измеренным для разбавленных водных растворов солей [86]. В противоположность этому поведение жировой ткани более похоже на поведение неводных жидкостей (см., например, данные для спиртов в работе [60]), что, вероятно, объясняется низким содержанием воды в жировой ткани.
Обычно скорость звука растет при повышении гидростатического давления. Следствием этого является нелинейный характер распространения ультразвуковых волн (см. разд. 4.3.6 и 4.3.8). Результаты измерения зависимости скорости звука от давления использовались для оценки нелинейного параметра В/А (разд. 1.8) мягких тканей и растворов макромолекул. При этом было установлено, что нелинейный параметр жировой ткани существенно превосходит его значения для всех других мягких тканей нежировой природы [59]. Этот результат представляется интересным в свете отмеченных ранее различий в температурном коэффициенте скорости звука между жировой и нежировой тканью.
5.3.3. ВЛИЯНИЕ СТРУКТУРНЫХ КОМПОНЕНТОВ ТКАНИ
Анализ данных, представленных на рис. 5.3 для мягких тканей (за исключением жировой ткани), показывает, что более высокое значение скорости звука в одной ткани по сравнению с другой коррелирует с более высоким содержанием в ней белков, в особенности структурного коллагена, и с более низким содержанием воды [24, 37, 70]. С другой стороны, вариации скорости в тканях одного и того же типа (например, в печени) мало зависят от содержания коллагена и, по-видимому, определяются в основном процентным содержанием воды (см. разд. 4.5.2.6 и работу Сарвазяна и др. [83]). Аналогичные результаты были получены и для ткани мозга. В частности, различия скорости звука в мозге взрослого человека и ребенка или плода вполне объясняется различиями в содержании воды в соответствующих тканях [57, 91] (рис. 5.5). Не столь очевидная картина наблюдается в случае артериальной ткани, где скорость звука растет с ростом содержания коллагена и уменьшается при относительном увеличении холестерина, причем зависимость скорости от содержания коллагена более существенна [80].
Низкое значение скорости звука в жире определяет его важную (с акустических позиций) роль как составного элемента некоторых тканей. В нормальной печени и печени с патологическими изменениями низкое содержание воды приводит к более высокому значению скорости звука. Если же изменения в печени сопровождаются повышением содержания жировой компоненты, то скорость звука будет уменьшаться [7, 93]. Средняя скорость звука в молочной железе, характеризующейся высоким содержанием жира, имеет сравнительно низкое значение, которое с возрастом уменьшается еще больше из-за прогрессирующей замены железистой ткани жиром [2, 56]. Молочная железа кормящей женщины из-за высокого содержания молока и разрастания железистой ткани характеризуется повышенным значением скорости звука (рис. 5.2). Анализ картины пространственного распределения акустических параметров в тонких срезах удаленной ткани молочной железы [30] наглядно показывает, что вариации скорости звука и других акустических параметров в норме и при патологии определяются в основном относительным содержанием жировой компоненты.
Для получения количественных данных и характеризации тканей по акустическим изображениям идеально было бы провести точные измерения возможно большего числа акустических параметров [3]. Однако в тех случаях, когда имелась возможность измерения скорости звука или ее пространственного распределения [6, 30, 39], этот параметр часто оказывался более полезным при выявлении различий между нормальной и патологической тканью по сравнению с коэффициентом затухания или коэффициентом обратного рассеяния. Отчасти это можно объяснить тем, что скорость звука удается измерить с более высокой точностью и надежностью в сравнении с затуханием или рассеянием звука. Предварительные результаты исследования патологических изменений печени человека свидетельствуют о том, что при диагностике цирроза печени как дополнительный диагностический показатель величина скорости звука действительно может быть более информативной, чем коэффициент затухания. В работе [44] показано, что скорость звука имеет четко различающиеся значения в нормальной печени, печени с ожирением и печени, пораженной циррозом. Следует, однако, отметить, что Доуст и др. [22] получили несовпадающие результаты для различных образцов циррозной печени. Было высказано предположение, что такое расхождение может объясняться различием в причинах возникновения цирроза (и, следовательно, различием в видах цирроза) у тех групп людей, которые проходили обследование в Австралии и Японии. Справедливость этого предположения подтверждается данными Циммермана и Смита [93], полученными в результате измерений на образцах фиксированной печени человека. По данным этих авторов, изменения скорости звука при циррозе носят неоднозначный характер. В начальной и средней стадии этого заболевания скорость звука уменьшается по сравнению с ее значением в нормальной печени, тогда как на стадии ярко выраженного цирроза величина скорости близка к ее значению в норме.
Влияние патологических изменений на скорость звука исследовалось также применительно к тканям других типов. В этом плане мозг, по-видимому, привлек наибольшее внимание. Было показано, что в большинстве случаев различные патологии мозга (за исключением кровотечений и гидроцефалии) приводят к увеличению скорости звука. Однако пока экспериментальных данных очень мало, и работа Кремкау и др. [58] является по существу единственной, где исследовалось влияние различных патологий мозга.
Скорость звука является очень важной характеристикой биологических тканей. Она более объективно характеризует процесс распространения акустических волн в тканях по сравнению, например, с коэффициентами затухания или рассеяния, поскольку сами эти коэффициенты в определенной степени зависят от вариаций скорости звука. К настоящему времени разработано очень много различных методов измерения скорости звука, хотя часто эти методы трудно применить к биологическим тканям. По существу методы измерений на различных тканях in vivo только начинают развиваться. В тех случаях, когда условия позволяют провести измерения скорости звука, эти измерения могут быть выполнены с более высокой точностью и надежностью, чем измерения затухания или рассеяния звука.
Усилия, которые требуются в настоящее время для преодоления трудностей, возникающих на пути развития методов измерения in vivo и получения количественной информации при анализе изображений пространственного распределения скорости звука, с успехом могут быть вознаграждены диагностической эффективностью этого метода. Кроме того, с помощью изображений пространственного распределения скорости звука можно добиться улучшения качества изображений другого типа, например составных изображений распределения амплитуд сигналов обратного рассеяния. Это достигается посредством соответствующей корректировки с учетом флуктуаций скорости звука, которые обычно приводят к пространственному искажению и размытию эхо-изображений [51].
При проведении измерений скорости звука необходимо учитывать ее зависимость от температуры. Температурный коэффициент скорости может быть использован для дистанционного контроля за относительными распределениями температуры.
1. Akamatsu, К., Miyauchi, S., Nishimura N. Ohkubo, Н., & Ohta, Y. (1985) A simple new method for in vivo measurement of ultrasound velocity in liver and its clinical usefulness. Proc. 4th Meeting of the World Federation for Ulrasound in Medicine and Biology. Gill, R. W. & Dadd, M. J. (eds.), Perga-mon Press, Sydney, p. 522.
2. Bamber, J. C. (1983a) Ultrasonic propagation properties of the breast Ultrasonic examination of the breast. Jellins, J. & Kobayashi, T. (eds.), John Wiley and Sons, Chichester, 37—44.
3. Bamber, J. C. (1983b) Ultrasonic tissue characterization in cancer diagnosis and management. RNM Images, Oct. '83, 12—19.
4. Bamber, J. C. & Abbott, C. (1985) The feasibility of measuring average speed of sound in tissues using a real-time scanner. Proc. 4th Meeting of the World Federation for Ultrasound in Medicine and Biology. Gill, R. W. & Dadd, M. J. (eds.), Pergamon Press, Sydney, p. 517.
5. Bamber, J. C. & Hill, C. R. (1979) Ultrasonic attenuation and propagation speed in mammalian tissues as a function of temperature. Ultrasound Med. Biol. 5, 149—157.
6. Bamber, J. C. & Hill, C. R. (1981) Acoustic properties of normal and cancerous human liver — I dependence on pathological condition. Ultrasound Med. Biol., 7, 121—133.
7. Bamber, J. C. Hill, C. R. & King, J. A. (1981) Acoustic properties of normal and cancerous human liver — II dependence on tissue structure. Ultrasound Med. Biol., 7, 135—144.
8. Barger, J. E. (1979) Attenuation and dispersion of ultrasound in cancellous bone. Ultrasonic tissue characterization II. Linzer, M. (ed.), NBS Special Publication 525, U.S. Government Printing Office, Washington, D. C, 197—201.
9. Beyer, R. T. & Letcher, S. V. (1969) Physical ultrasonics. Academic Press, New York.
10. Bhagat, P., Hajjar, W., & Kadaba, M. (1976) Measurement of the acoustic properties of a nerve-muscle preparation as a function of physiological state. Ultrasonics, Nov. '76, 283—285.
11. Bowen, Т., Conner, W. G., Nasoni, R. L., Pifer, A. E. & Sholes, R. R. (1979) Measurement of the temperature dependence of the velocity of ultrasound in tissues. Ultrasonic tissue characterization II. Linzer, M. (ed.) U. S. Government Printing Office, Washington, D. C. NBS Special Publication 525, 57—61.
12. Buschmann, W, Voss, M., & Kemmerling, S. (1970) Acoustic properties of normal human orbit tissues. Opthalmol. Res., 1, 354—364.
13. Carson, P. L., Meyer, C. R. & Scherzinger, A. L. (1981) Breast imaging in coronal planes with simultaneous pulse echo and transmission ultrasound. Science, 214, 1141—1143.
14. Carstensen, E. L. (1954) Measurement of dispersion of velocity of sound in liquids. J. acoust. Soc. Amer. 26, 858—861.
15. Carstensen, E. L. & Schwan, H. P. (1959) Acoustic properties of hemoglobin solutions. J. acoust. Soc. Amer., 31, 305—311.
16. Cetas, Т. C. & Connor, W. G. (1978) Thermometry considerations in localized hyperthermia. Med. Phys. 5, 79—91.
17. Chenevert, T. L., Schmitt, R. M., Carson, P. L., Bland, P. H., Meyer, C. R., Adler, D. D., & Samuels, В. T. (1984) The potential of ultrasonic CT for breast cancer diagnosis, /. Ultrasound in Med., Supplement to Vol. 3, No. 9, (Proc. 29th Annual Meeting of the American Inst, of Ultrasound in Medicine, Sept. 1984) p. 127 (abstract only).
18. Chivers, R. C. & Parry, R. J. (1978) Ultrasonic velocity and attenuation in mammalian tissues. J. acoust. Soc. Amer., 63, 940—953.
19. Chubachi, N. (1981) Mechanically scanned acoustic microscope. Japan J. App. Phys. 21, Supplement 21—3, 7—10.
20. Coppens, A. B. (1981) Simple equations for the speed of sound in Neptunian waters. J. acoust. Soc. Amer. 69, 862—863.
21. Del Grosso, V. A. & Mader, C. W. (1972) Speed of sound in pure water. J. Acoust. Soc. Amer. 52, 1442—1446.
22. Doust, В., Robinson, D. E., Chen, C. F., & Wilson, L. S. (1985) Ultrasonic speed and attenuation determinations in cirrhosis of the liver. Proc. 4th Meeting of the World Federation for Ultrasound in Medicine and Biology. Gill, R. W. & Dadd, M. J. (eds.), Pergamon Press, Sydney, p. 80.
23. Dunn, F. (1974) Attenuation and speed of ultrasound in lung. J. acoust. Soc. Amer., 56, 1638—1639.
24. Dunn, F. (1976) Ultrasonic attenuation, absorption and velocity in tissues and organs. Ultrasonic tissue characterization. Linzer, M. (ed.) U. S. Govt. Printing Office, Washington, D. C., NBS Special Publication 453, 21—28.
25. Dunn, F. & Fry, W. J. (1961) Ultrasonic absorption and reflection by lung tissue. Phys. Med. Biol, 5, 401—410.
26. Dunn, F., Edmonds, P. D., & Fry, W. J. (1969) Absorption and dispersion of ultrasound in biological media. Biological engineering. Schwan, H. P. (ed.), McGraw-Hill, New York, 205—332.
27. Edmonds, P. D., Reyes, Z., Parkinson, D. В., Filly, R. A., & Busey, H. (1979) A human abdominal tissue phantom. Ultrasonic tissue characterization II. Linzer, M. (ed.), NBS Special Publication 525, U.S. Government Printing Office, Washington, D.C, 323—326.
28. Eggleton, R. C. & Whitcomb, J. A. (1979) Tissue simulators for diagnostic ultrasound. Ultrasonic tissue characterization II. Linzer, M. (ed.), NBS Special Publication 525, U. S. Government Printing Office, Washington, D. C., 323—326.
29. Embree, P. M., Tervola, К. M. U, Foster, S. G., & O'Brien, Jr. W. D. (1985) Spatial distribution of the speed of sound in biological materials with the scanning laser acoustic microscope. IEEE Trans. Sonics and Ultrasonics, SU—32, 341—350.
30. Foster, F. S., Strban, M., & Austin, G. (1984) The ultrasound macroscope: initial studies on breast tissue. Ultrasonic Imaging, 6, 243—261.
31. Frizzell, L. A. & Gindorf, J. D. (1981) Measurement of ultrasonic velocity in several biological tissues. Ultrasound Med. Biol., 7, 385—387.
32. Giacomini, A. (1947) Ultrasonic velocity in ethanol-water mixtures. /. Acoust. Soc. Amer., 19, 701—702.
33. Glover, G. H. & Sharp, J. C. (1977) Reconstruction of ultrasound propagation speed distributions in soft tissue: time-of-flight tomography. IEEE Trans. Son. Ultrason., 24, 229—234.
34. Goldman, D. E. & Hueter, T. F. (1956) Tabular data of the velocity and absorption of high-frequency sound in mammalian tissues. J. acoust. Soc. Amer., 28, 35—37.
35. Goldman, D. E. & Richards, J. R. (1954) Measurement of high frequency sound velocity in mammalian soft tissues. J. acoust. Soc. Amer. 26, 981—983.
36. Goss, S. A., Johnston, R. L., & Dunn, F. (1978) Comprehensive compilation of empirical ultrasonic properties of mammalian tissues. /. acoust Soc. Amer., 64, 423—457.
37. Goss, S. A., Johnston, R. L., Maynard, V., Nider, L., Frizzell, L. A., O'Brien, Jr. W. D., & Dunn, F. (1979) Elements of tissue characterization part II; ultrasonic propagation parameter measurements. Ultrasonic tissue characterization II. Linzer, M. (ed.) NBS Special Publication 525, U. S. Govt. Printing Office, Washington, D. C, 43—51.
38. Grant, D. R. & Bernadin, J. E. (1981) Measurement of sound velocity with the scanning laser acoustic microscope. / acoust. Soc. Amer., 69, 866—868.
39. Greenleaf, J. F. & Bahn, R. C. (1981) Clinical imaging with transmissive ultrasonic computerized tomography. IEEE Trans. BME-28, 177—185.
40. Greenleaf, J. E, Johnson, S. A., Samayoa, W. E, & Duck, F. A. (1975) Twodimensional acoustic velocity distributions in tissues using an algebraic reconstruction technique. Ultrasonics Int. Conf. Proc, IPC Science and Technology Press, Guildford, 190—194.
41. Greenspan, M. & Tschiegg, С. E. (1957) Rev. Sci. Inst. 28, 897. 42. Haumschild, D. J. & Greenleaf, J. F. (1983) A crossed beam method for ultrasonic speed measurement in tissue. Ultrasonic Imaging, 5, p. 168.
43. Hayney, M. J. & O'Brien, Jr. W. D. (1982) Ultrasonic tomography for differential thermography. Acoustical Imaging Volume 12. Ash, E. A. & Hill, C. R. (eds.) Plenum Press, New York, 589—597.
44. Hayashi, N., Tamaki, N., Yamammoto, K., Senda, M., Yonekura, Y, Torizuka, K., Ogawa, Т., Katakura, K., & Umemura, S. (1985) In vivo measurement of sound speed in normal and abnormal livers using a high resolution ultrasonic scanner. Proc. 4th Meeting of the World Federation for Ultrasound in Medicine and Biology. Gill, R. W. and Dadd, M. J. (eds.), Pergamon Press, Sydney, P. 520.
45. Heyser, R. C. & LeCroisette, D. H. (1974) A new ultrasonic imaging system using time delay spectrometry. Ultrasound Med. Biol., 1, 119—131.
46. Iinuma, K., Sumino, Y, Hirama, M., Okazaki, K., Sato, Т., & Sasaki, H. (1985) A proposal of crossed beam method using a linear array probe for in vivo measurement of sound velocity of tissue. Proc. 4th Meeting of the World Federation for Ultrasound in Medicine and Biology. Gill, R. W. & Dadd, M. J. (eds.), Pergamon Press, Sydney, p. 515.
47. Jellins, J. & Kossoff, G. (1973) Velocity compensation in water-coupled breast echography. Ultrasonics, 11, 223—226.
48. Johnson, S. A., Christensen, D. A., Johnson, С. C, Greenleaf, J. E, & Rajagopalan, B. (1977) Non-intrusive measurement of microwave and ultrasound induced hyperthermia by acoustic temperature tomography. Ultrasonics Symp. Proc. IEEE Cat. No. llCh\264—\SU, 977—982.
49. Johnston, R. L., Goss, S. A., Maynard, V, Brady, J. K., Frizzell, L. A., O'Brien, Jr. W. D., & Dunn, F. (1979) Elements of tissue characterization: part I ultrasonic propagation properties. Ultrasonic tissue characterization II. Linzer, M. (ed.), NBS Special Publication 525, U. S. Government Printing Office, Washington, D. C, 19—27.
50. Kaye, G. W. C. & Laby, Т. H. (1966) Tables of physical and chemical constants and some mathematical functions. Thirteenth edition. Longmans, Green and Co., London.
51. Kim, J. H., Park, S. В., & Johnson, S. A. (1984) Tomographic imaging of ultrasonic reflectivity with correction for acoustic speed variations. Ultrasonic Imaging, 6, 304—312.
52. Kinsler, L. E., Frey, A., Coppens, A. B. & Saunders, J. V. (1982) Fundamentals of acoustics. Third edition. John Wiley and Sons, New York, p. 397.
53. Kittinger, (1977) Correction for transducer influence on sound velocity measurements by the pulse echo method. Ultrasonics, 15, 30—32.
54. Klemin, V. A., Karev, I. D., Sarvazyan, A. P., Timokhina, Z. M., Puchkin, V. V. & Mayorov, E. A. (1981) Relation of acoustic characteristics of human gastric juice to its composition for some stomach diseases. Studia Biophysica 84, 139—144.
55. Koch, R., Whiting, J. E, Price, D. C, McCaffrey, J. E, Kossoff, G., & Reeve, T. S. (1983) Transmission tomography and B-scan imaging of the breast. Ultrasonic examination of the breast. Jellins, J. & Kobayashi, T. (eds.), John Wiley and Sons, Chichester, 235—239.
56. Kossoff, G., Kelly Fry, E., & Jellins, J. (1973) Average velocity of ultrasound in the human female breast. J. acoust. Soc. Amer., 53, 1730—1736.
57. Kremkau, F. W., Barnes, R. W., & McGraw, C. P. (1981) Ultrasonic attenuation and propagation speed in normal human brain. J. acoust. Soc. Amer., 70, 29—38.
58. Kremkau, F. W., McGraw, C. P., & Barnes, R. W. (1979) Acoustic properties of normal and abnormal human brain. Ultrasonic tissue characterization II. Linzer, M. (ed.), NBS Special Publication 525, U. S. Government Printing Office, Washington, D. C, 81—84.
59. Law, W. K., Frizzell, L. A., & Dunn, F. (1985) Determination of the nonlinearity parameter B/A of biological media. Ultrasound Med. Biol. 11, 307—318.
60. Litovitz, T. A. & Davis, С. M. (1965) Structural and shear relaxation in liquids. Physical acoustics Volume 2A. Mason, W. P. (ed.) Academic Press, New York, 281—349.
61. Liu, С. H. & Yeh, К. C. (1980) Statistics of pulse arrival time in turbulent media. J. opt. Soc. Amer., 70, 168—172.
62. Ludwig, G. D. (1950) The velocity of sound through tissues and acoustic impedance of tissues. J. acoust. Soc. Amer. 22, 862—866.
63. McSkimin, H. J. (1964) Ultrasonic methods of measuring the mechanical properties of liquids and solids. Physical acoustics: principles and methods, Vol. 1—Part A., Mason, W. P., (ed.), Academic Press, New York, Ch. 10, 271—334.
64. Manoharan, A., Robinson, D. E., Wilson, L. S. Chen, С. E, & Griffiths, K. A. (1985) Ultrasonic characterization of splenic tissue: a clinical study in patients with myelofibrosis. Proc. 4th Meeting of the World Federation for Ulrasound in Medicine and Biology. Gill, R. W. & Dadd, M. J. (eds.), Pergamon Press, Sydney, p. 113.
65. Matheson, A. J. (1971) Molecular acoustics. Van Nostrand, New York. 66. Mesdag, P. R. de Vries, D., & Berkhout, A. J. (1982) An approach to tissue characterization based on wave theory using a new velocity analysis technique. Acoustical imaging, Vol. 12. Ash, E. A. & Hill, C. R. (eds.), Plenum Press, New York, pp. 479—491.
67. Millero, F. J. & Kubinski, T. (1975) Speed of sound in seawater as a function of temperature and salinity at 1 atm. J. acoust. Soc. Amer. 57, 312—319.
68. Mol, C. R. & Breddels, P. A. (1982) Ultrasound velocity in muscle. J. acoust. Soc. Amer., 71, 455—461.
69. Nasoni, R. L., Bowen, Т., Conner, W. G., & Sholes, R. R. (1979) In-vivo temperature dependence of ultrasound speed in tissue and its applications to noninvasive temperature monitoring. Ultrasonic Imagaing, 1, 34—43.
70. O'Brien, Jr., W. D. (1977) The relationship between collagen and ultrasonic attenuation and velocity in tissue Ultrasonics International 1977 Conference Proc. IPC Business Press, Guildford, 194—205.
71. Ohtsuki, S., Soetanto, K., & Okujima, M. (1985) A technique with reference points image for in vivo measurement of sound velocity. Proc. 4th Meeting of the World Federation for Ultrasound in Medicine and Biology. Gill, R. W. & Dadd, M. J. (eds.), Pergamon Press, Sydney, p. 521.
72. Papadakis, E. P. (1964) Ultrasonic attenuation and velocity in three transformation products in steel. J. Appl, Phys., 35, 1474—1482.
73. Papadakis, E. P. (1966) Ultrasonic diffraction loss and phase change in anisotropic materials. J. acoust. Soc. Amer., 40, 863—876.
74. Papadakis, E. P. (1972) Absolute accuracy of the pulse-echo everlap method and the pulse-superposition method for ultrasonic velocity. J. acoust. Soc. Amer.
52, 843—846.
75. Pellam, J. R. & Gait, J. K. (1946) Ultrasonic propagation in liquids: I. Application of pulse technique to velocity and absorption measurements at 15 megacycles. /. Chem. Phys., 14, 608—614.
76. Ragozzino, M. (1981) Analysis of the error in measurement of ultrasound speed in tissue due to waveform deformation by frequency dependent attenuation. Ultrasonics, 12, 135—138.
77. Redwood, M. (1963) A study of waveforms in the generation and detection of short ultrasonic pulses. Appl. Mat. Res., April 1983, 76—84.
78. Robinson, D. E., Chen, E, & Wilson, L. S. (1982) Measurement of velocity of propagation from ultrasonic pulse-echo data. Ultrasound Med. Biol. 8, 413—420.
79. Robinson, Т. C. & Lele, P. P. (1972) An analysis of lesion development in the brain and in plastics by high-intensity focused ultrasound at lowmegahertz frequencies. J. acoust. Soc. Amer., 51, 1333—1351.
80. Rooney, J. A., Gammell, P. M., Hestenes, J. D., Ghin, H. P., & Blankenhorn, D. H. (1982) Velocity and attenuation of sound in arterial tissues. J. acoust. Soc. Amer., 71, 462—466.
81. Сарвазян А. П.— Мол. биол., 1983, т. 17, вып. 5, с. 916—927.
82. Sarvazyan, А. Р. (1982) Development of methods of precise ultrasonic measurements in small volumes of liquids. Ultrasonics 20, 151—154.
83. Sarvazyan, A. P. Lyrchikov, A. G. & Gorelov, S. E. (1987) Dependence of ultrasonic velocity in rabbit liver on water content and structure of the tissue. Ultrasonics 25, 244—247.
84. Seki, H., Granato, A., & Truell, R. (1956) Diffraction effects in the ultrasonic field of a piston source and their importance in the accurate measurement of attenuation. /. acoust. Soc. Amer., 28, 230—238.
85. Sinclair, D. A., Smith, I. R., & Wickramasinghe, H. K. (1982) Recent developments in scanning acoustic microscopy. The Radio and Electronic Engineer, 52, 479—493.
86. Stuehr, J. & Yeager, E. (1965) The propagation of ultrasonic waves in electrolytic solution. Physical acoustics Volume 2A. Mason, W. P. (ed.) Academic Press, New York, 351—462.
87. Subrahmanyam, S. V., Khan, V. H., & Raghavan, С. V. (1969) Interferometric measurement of ultrasonic velocity in liquids — effect of diffraction. J. acoust. Soc. Amer., 46, 272.
88. Thijssen, J. M., Mol, H. J. M., & Timmer, M. R. (1985) Acoustic parameters of ocular tissues. Ultrasound Med. Biol., 11, 157—161.
89. Van Venrooij, G. E. P. M. (1971) Measurement of sound velocity in human tissue. Ultrasonics, 9, 240—242.
90. Verhoef, W. A., Cloostermans, M. J. Т. M., & Thijssen, J. M. (1985) Diffraction and dispersion effects on the estimation of ultrasound attenuation and velocity in biological tissues. IEEE Trans. Biomed. Eng. BME-32, 521—529.
91. Wladimiroff, J. W., Craft, I. L., & Talbert, D. G. (1975) In vitro measurements of sound velocity in human fetal brain tissue. Ultrasound Med. Biol., 1, 377—382.
92. Yoon, H. S. & Katz, J. L. (1979) Ultrasonic properties and microtexture of human cortical bone. Ultrasonic tissue characterization II. Linzer, M. (ed.), NBS Special Pub. 525, U. S. Governmerl Printing Office, Washington, D. C, 189—196.
93. Zimmermann, K. P. & Smith, J. C. (1983) Ultrasound velocity in fixed human liver: empirical anova and regression modelling on histologically assessed abnormalities. Ultrasonic Imaging, 5, 280—294.
ОТРАЖЕНИЕ И РАССЕЯНИЕ УЛЬТРАЗВУКА
Р. Дикинсон
Рассеяние ультразвуковых волн возникает в тех случаях, когда волны распространяются в акустически неоднородных средах. При этом часть энергии падающей волны переизлучается в виде рассеянных волн, которые отличаются от исходной волны либо задержкой по времени, либо изменением направления распространения. В гл. 1 был рассмотрен простейший случай нормального падения волны на неоднородность в виде плоской границы раздела между двумя средами с различными акустическими свойствами. При анализе этого случая использовалось понятие удельного акустического импеданса. Следует отметить, что в мягких тканях подобные границы встречаются редко. Значительно чаще неоднородности в таких средах имеют сложную форму и различные размеры, причем их местоположение и ориентация зачастую носят случайный характер. При В-сканировании полутоновое изображение, т. е. изображение с большим числом градаций яркости, формируется в основном волнами, рассеянными на подобных мелкомасштабных структурах. Помимо систем акустической визуализации (акустоскопии) явление рассеяния лежит в основе работы доплеровских систем и ряда устройств другого типа, о которых речь пойдет в гл. 9—11. Понимание физических механизмов процесса рассеяния необходимо для оценки возможностей таких систем, поэтому основная задача данной главы — провести анализ той полезной информации, которая содержится в рассеянной волне.
Ниже дается обзор современного состояния теории рассеяния ультразвуковых волн и ее применения в медицинской акустике. В следующем разделе мы более подробно остановимся на одном из интересных теоретических подходов к решению задачи рассеяния. Здесь будут приведены обобщенные уравнения и соответствующие теоретические выводы. Отметим, что трудно дать строгую постановку задачи рассеяния применительно к биологическим тканям, поскольку их акустические свойства в масштабе, меньшем длины акустической волны, неизвестны. Это заставляет использовать для описания свойств тканей те или иные упрощенные модели, анализу которых также отводится определенное место в данной главе. Затем обсуждаются результаты экспериментальных исследований рассеяния ультразвука в тканях и приводятся те выводы, которые можно сделать об акустических свойствах исследуемой ткани на основе анализа рассеянного поля.
В большинстве теорий рассеяния рассматриваются плоские монохроматические волны, тогда как акустическое изображение при В-сканировании формируется за счет рассеяния импульсных сигналов. В связи с этим один из разделов данной главы специально посвящен теории рассеяния акустических импульсов и ее взаимосвязи с параметрами изображения, получаемого при В-сканировании. Здесь же обсуждается влияние движений биологических тканей на рассеянную волну.
В последние годы было разработано несколько методов, обеспечивающих возможность как представления рассеянного поля в виде некоторого «изображения», так и объективного анализа этого изображения с целью получения количественных данных о рассеивающей среде (см. гл. 10). Мы детально рассмотрим один из таких методов, который иногда называют импедиографией и который наглядно демонстрирует взаимосвязь между отражением и рассеянием ультразвука. И наконец, мы кратко обсудим ряд других методов, которые могут оказаться пригодными для наших целей, и рассмотрим возможные направления дальнейших исследований.
6.1.2. СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ РАССЕЯНИЯ
Теория рассеяния звука в тканях человеческого организма была разработана Чиверсом [15]. Некоторые положения этой теории мы будем использовать в последующих разделах при детальном рассмотрении конкретных задач рассеяния. Отметим также, что многие положения теории Чиверса изложены в обстоятельной монографии Ишимару [28], посвященной задачам рассеяния излучения различной природы.
В случае, когда длина акустической волны ![]() много меньше характерного размера неоднородностей
много меньше характерного размера неоднородностей ![]() (где
(где ![]() — некий усредненный параметр, например радиус корреляции), задача рассеяния может быть рассмотрена с помощью двух различных подходов. В первом из них, который называется лучевым приближением или приближением геометрической акустики, влияние флуктуаций скорости звука в среде определяется на основе принципа Ферма. Такой подход позволяет получить выражения для среднеквадратического отклонения лучей, прошедших определенный путь в среде [14]. Лучевое приближение справедливо при условии, что
— некий усредненный параметр, например радиус корреляции), задача рассеяния может быть рассмотрена с помощью двух различных подходов. В первом из них, который называется лучевым приближением или приближением геометрической акустики, влияние флуктуаций скорости звука в среде определяется на основе принципа Ферма. Такой подход позволяет получить выражения для среднеквадратического отклонения лучей, прошедших определенный путь в среде [14]. Лучевое приближение справедливо при условии, что ![]() где L — путь, пройденный лучом. Чиверс использовал именно такой подход при анализе распространения ультразвуковых волн в биологических тканях. Второй метод, который описал Ушински [54], применим в случае, когда однократное рассеяние на неоднородности мало, т. е. выполняется условие
где L — путь, пройденный лучом. Чиверс использовал именно такой подход при анализе распространения ультразвуковых волн в биологических тканях. Второй метод, который описал Ушински [54], применим в случае, когда однократное рассеяние на неоднородности мало, т. е. выполняется условие ![]() , где n — среднеквадратическое отклонение показателя преломления среды. В отличие от лучевого приближения во втором методе нет столь строгих ограничений на величину L, поэтому суммарное рассеяние может быть весьма значительным. Другими словами, данный подход можно применить для исследования процессов многократного рассеяния. Ушински вывел ряд дифференциальных уравнений для различных статистических моментов поля и получил решения этих уравнений. На основе полученных решений он провел анализ влияния статистических свойств среды на процесс распространения акустических волн. Так, например, ему удалось показать, что первый статистический момент поля дает затухание, обусловленное рассеянием, второй момент определяет пространственную автокорреляционную функцию, функция автокорреляции в частотной области дает усредненную огибающую импульса, а четвертый момент — флуктуации интенсивности.
, где n — среднеквадратическое отклонение показателя преломления среды. В отличие от лучевого приближения во втором методе нет столь строгих ограничений на величину L, поэтому суммарное рассеяние может быть весьма значительным. Другими словами, данный подход можно применить для исследования процессов многократного рассеяния. Ушински вывел ряд дифференциальных уравнений для различных статистических моментов поля и получил решения этих уравнений. На основе полученных решений он провел анализ влияния статистических свойств среды на процесс распространения акустических волн. Так, например, ему удалось показать, что первый статистический момент поля дает затухание, обусловленное рассеянием, второй момент определяет пространственную автокорреляционную функцию, функция автокорреляции в частотной области дает усредненную огибающую импульса, а четвертый момент — флуктуации интенсивности.
Если размеры неоднородностей сравнимы с длиной волны или меньше ее (по-видимому, это условие выполняется в биологических тканях), то взаимодействие ультразвука со средой в значительной степени будет определяться дифракционными эффектами. Именно этому случаю рассеяния мы уделим основное внимание в данной главе.
В настоящее время имеется очень мало экспериментальных данных о микромасштабных структурах биологических тканей и их пространственном распределении. Возможно, что развитие акустической микроскопии (гл. 9) позволит изменить сложившуюся ситуацию. Тем не менее вполне достаточно рассматривать биологическую ткань как случайно-неоднородную среду, свойства которой описываются статистически. Такой подход привел к разработке двух моделей, которые поддаются теоретическому анализу и служат для исследования рассеивающих свойств биологических тканей. Эти модели будут подробно рассмотрены в разд. 6.3.
Как правило, проводившиеся теоретические оценки были основаны на использовании борновского приближения, в рамках которого не учитывается многократное рассеяние. Обоснованием этому служили малые значения сечений рассеяния, полученные в эксперименте для биологических тканей. Одним из следствий многократного рассеяния является искажение профиля акустического пучка, вызванное флуктуациями показателя преломления. Учет этого эффекта можно было бы рассматривать как первый шаг на пути к полному анализу процесса рассеяния.
Заключительная часть данной главы посвящена рассмотрению случая, когда ![]() . Такая задача может быть исследована с помощью двух моделей, которые ранее уже упоминались. Следует отметить, что именно этот случай наиболее часто возникает в реальных ситуациах при исследовании рассеяния и, в частности, обратного рассеяния в биологических средах. Рассеяние при
. Такая задача может быть исследована с помощью двух моделей, которые ранее уже упоминались. Следует отметить, что именно этот случай наиболее часто возникает в реальных ситуациах при исследовании рассеяния и, в частности, обратного рассеяния в биологических средах. Рассеяние при ![]() подробно рассмотрено Ушински (сюда относится случай искажения профиля пучка в биологической ткани), поэтому здесь мы его обсуждать не будем.
подробно рассмотрено Ушински (сюда относится случай искажения профиля пучка в биологической ткани), поэтому здесь мы его обсуждать не будем.
6.1.3. РАССЕЯНИЕ ВОЛН ПРОИЗВОЛЬНОЙ ПРИРОДЫ
Обзор различных теорий рассеяния ультразвуковых волн нельзя считать полностью законченным без упоминания большого числа работ из других областей, связанных с исследованием рассеяния излучения какой-либо другой (не акустической) природы. Рассеяние — это явление, общее для всех волн, будь то электромагнитное излучение, сейсмические волны, гидролокационные сигналы или, наконец, волны, описывающие движение ядерных частиц. Во многом теории рассеяния, разработанные для излучений различного типа, сходны между собой. Различие между ними может проявляться в добавлении тех или иных членов в общее волновое уравнение. Теория рассеяния импульсных ультразвуковых сигналов имеет много общего с теорией, разработанной ранее для радиолокационных сигналов, причем большое количество примеров из теории радиолокации содержится в упомянутой монографии Ишимару. Велико прикладное значение явления рассеяния акустических волн: оно использовалось при эхо-локации рыбных косяков на морских отмелях, в исследованиях дна океана, а также в неразрушающем контроле металлов [27].
Рассеяние возникает в результате взаимодействия распространяющейся волны с неоднородностями среды, и это взаимодействие определяется неоднородным волновым уравнением. В зависимости от конкретных условий возможны различные формулировки волнового уравнения. Мы рассмотрим случай слабонеоднородной среды, т. е. будем считать, что в среде отсутствует поглощение и флуктуации плотности ![]() и сжимаемости
и сжимаемости ![]() среды малы по сравнению со средними значениями
среды малы по сравнению со средними значениями ![]() и
и ![]() внутри некоторого замкнутого объема V, в котором локализованы неоднородности. Вне этого объема
внутри некоторого замкнутого объема V, в котором локализованы неоднородности. Вне этого объема ![]() и
и ![]() обращаются в нуль. Таким образом,
обращаются в нуль. Таким образом,
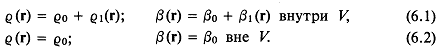
Кроме того, будем считать, что на поверхности, ограничивающей объем V,

Для удобства введем следующие параметры:
![]()
Используя введенные обозначения, волновое уравнение можно представить в виде [38]
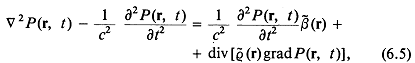
где ![]() .
.
Это уравнение можно решить методом функций Грина [37], рассматривая правую часть как член, описывающий источник, и используя функцию Грина, представляющую собой решение данного уравнения в случае, когда правая часть описывает точечный источник.
Соответствующее решение есть
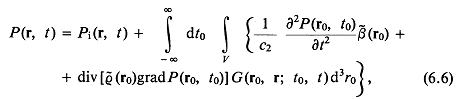
где
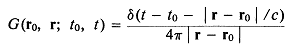
Интегральное уравнение для Р имеет точное решение только для ряда простых по геометрической конфигурации объектов. В общем случае решение находится с помощью приближенных методов, причем важное место среди них занимает борновское приближение. В рамках этого приближения интегральный член уравнения (6.6) преобразуется путем замены P(r, t) на Pi (р, t), где Pi описывает падающую волну, которая распространялась бы в объеме V при условии его однородности (т. е. когда ![]() и
и ![]() равны нулю). Обычно выражение для Pi (r, t) известно. Подчеркнем, что борновским приближением можно пользоваться только в случаях слабого рассеяния, когда оба параметра
равны нулю). Обычно выражение для Pi (r, t) известно. Подчеркнем, что борновским приближением можно пользоваться только в случаях слабого рассеяния, когда оба параметра ![]() и
и ![]() малы. Если эти условия не выполняются, то решение уравнения (6.6) ищется с помощью итерационного метода на основе последовательных приближений.
малы. Если эти условия не выполняются, то решение уравнения (6.6) ищется с помощью итерационного метода на основе последовательных приближений.
Таким образом, в борновском приближении
![]()
где Ps(r, t)=Pi(r, t) рассеянная волна, описиваемая вырожением
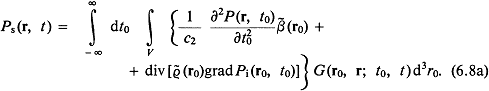
В качестве примера рассмотрим случай, когда падающая волна является плоской волной с угловой частотой ![]() и амплитудой ро, т. е.
и амплитудой ро, т. е.
![]()
Подстановка (6.9) в (6.8) дает
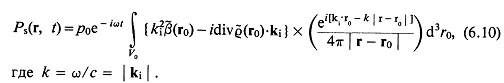
Поместим начало координат внутри рассеивающего объема V (рис. 6.1). Если расстояние от рассеивающей области до точки наблюдения велико по сравнению с линейными размерами этой области, то показатель экспоненты, стоящей под знаком интеграла в выражении (6.10), приближенно можно представить в виде
![]()
причем направление вектора ks совпадает с направлением г, а его модуль равен к (рис. 6.1). В результате
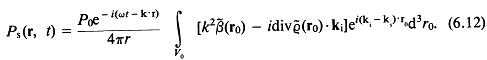
В данной главе мы используем метод фурье-преобразований, тогда как в гл. 1 анализ проводится с помощью преобразований Лапласа. С учетом этого можно видеть, что выражение (6.9) эквивалентно выражению (1.36), в котором мы положили ![]() .
.
Аналогичным образом, уравнение (6.12) на языке фурье-преобразований эквивалентно уравнению (1.48). Уравнение (6.12) описывает сферическую волну, исходящую из начала координат (см. разд. 1.3.2) и характеризующуюся анизотропным угловым распределением. Эта пространственная анизотропия определяется интегралом, входящим в уравнение (6.12).
Введем определения
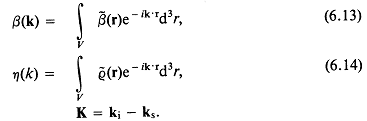
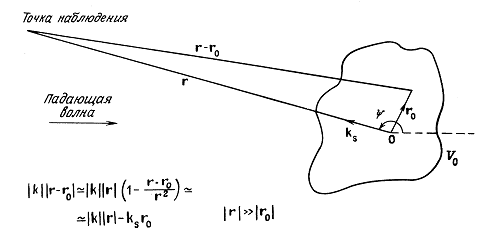
Рис. 6.1. Конфигурация, используемая при решении задачи рассеяния в приближении Борна (разд. 6.2.1).
Тогда
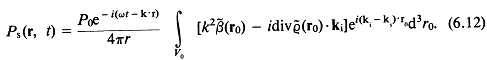
![]() — угол между направлениями падающей и рассеянной волн.
— угол между направлениями падающей и рассеянной волн.
Анализ полученного выражения позволяет сделать некоторые выводы. Прежде всего, если флуктуации плотности и сжимаемости достаточно малы и носят случайный характер, то модули |![]() | и |
| и |![]() | будут константами в пределах определенного интервала значений k, а амплитуда рассеянной волны будет пропорциональна k2. Такая зависимость соответствует случаю рэлеевского рассеяния и часто наблюдается в различных волновых полях. Угловая зависимость амплитуды рассеянного сигнала определяется пространственными флуктуациями сжимаемости и плотности. Если флуктуации сжимаемости изотропны, то и рассеянное поле будет изотропным. Изотропность флуктуаций плотности приводит к дипольному рассеянию, при котором рассеяние имеет резко направленный характер и сконцентрировано в прямом и обратном направлениях.
| будут константами в пределах определенного интервала значений k, а амплитуда рассеянной волны будет пропорциональна k2. Такая зависимость соответствует случаю рэлеевского рассеяния и часто наблюдается в различных волновых полях. Угловая зависимость амплитуды рассеянного сигнала определяется пространственными флуктуациями сжимаемости и плотности. Если флуктуации сжимаемости изотропны, то и рассеянное поле будет изотропным. Изотропность флуктуаций плотности приводит к дипольному рассеянию, при котором рассеяние имеет резко направленный характер и сконцентрировано в прямом и обратном направлениях.
Амплитуда рассеянной волны зависит от волнового вектора ks и угла рассеяния ![]() . Для дальнейшего анализа волновые векторы падающей и рассеянной волны удобно представить в сферических координатах, выбирая координатную систему так, чтобы одна из осей совпадала с направлением падающей волны. Однозначным образом геометрию задачи в этом случае можно определить с помощью четырех углов (задавая два угла для падающей волны и два — для рассеянной). В частности, для рассеянной волны вводятся азимутальный угол
. Для дальнейшего анализа волновые векторы падающей и рассеянной волны удобно представить в сферических координатах, выбирая координатную систему так, чтобы одна из осей совпадала с направлением падающей волны. Однозначным образом геометрию задачи в этом случае можно определить с помощью четырех углов (задавая два угла для падающей волны и два — для рассеянной). В частности, для рассеянной волны вводятся азимутальный угол ![]() и угол места
и угол места ![]() (рис. 6.2). При этом угол
(рис. 6.2). При этом угол ![]() можно выразить через углы
можно выразить через углы ![]() и
. Если, например, волновой вектор ki направлен вдоль оси у, то
и
. Если, например, волновой вектор ki направлен вдоль оси у, то
![]()
Аналогичным образом, углы ![]() и
и ![]() определяют ориентацию рассеивающего элемента относительно падающей волны. Эти углы являются сферическими координатами волнового вектора падающей волны в координатной системе, привязанной к рассеивающему элементу.
определяют ориентацию рассеивающего элемента относительно падающей волны. Эти углы являются сферическими координатами волнового вектора падающей волны в координатной системе, привязанной к рассеивающему элементу.
Таким образом, вектор К определяется модулем |ki| и углами ![]() и
и ![]() . Одно измерение рассеянного поля будет давать одно значе ние величины
. Одно измерение рассеянного поля будет давать одно значе ние величины ![]() . Как видно из выражений (6.13) и (6.14), функции
. Как видно из выражений (6.13) и (6.14), функции ![]() и
и ![]() сами зависят от
сами зависят от ![]() и
и ![]() .
.
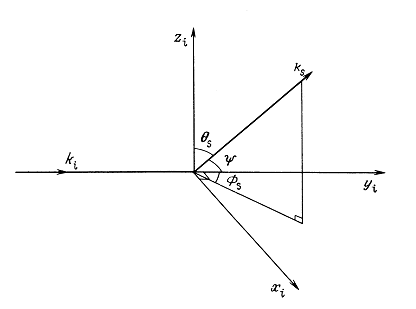
Рис. 6.2. Схема, определяющая углы рассеяния из разд. 6.2.1. Углы ![]() и
и ![]() — сферические координаты волнового вектора рассеянной волны ks относительно ki•ki. Система координат выбрана так, что волновой вектор падающей волны ki совпадает с осью у.
— сферические координаты волнового вектора рассеянной волны ks относительно ki•ki. Система координат выбрана так, что волновой вектор падающей волны ki совпадает с осью у.
Можно использовать аналогичную систему координат (здесь не показана), привязанную к рассеивателю, для задания ориентации вектора ki относительно рассеивате-ля. С этой целью вводятся углы ![]() и
и ![]() .
.
Чтобы получить значение функции ![]() в широком интервале изменения вектора К, необходимо провести измерения в некотором диапазоне частот, варьируя |ki| и углы
в широком интервале изменения вектора К, необходимо провести измерения в некотором диапазоне частот, варьируя |ki| и углы ![]() и
и ![]() . По результатам таких измерений с помощью фурье-преобразования можно реконструировать параметры
. По результатам таких измерений с помощью фурье-преобразования можно реконструировать параметры ![]() и
и ![]() . Такой подход известен как метод дифракционной томографии (см. разд. 9.5). Однако во многих случаях невозможно получить всю необходимую информацию — реально доступным является лишь ограниченный набор значений |ki| ,
. Такой подход известен как метод дифракционной томографии (см. разд. 9.5). Однако во многих случаях невозможно получить всю необходимую информацию — реально доступным является лишь ограниченный набор значений |ki| , ![]() и
и ![]() . В системах, где используется эхо-импульсный режим,
. В системах, где используется эхо-импульсный режим, ![]() и
и ![]() . В этом случае измерения рассеяния будут давать информацию только о величине
. В этом случае измерения рассеяния будут давать информацию только о величине ![]() . Следует также иметь в виду, что доступ ко многим участкам человеческого организма возможен лишь через некоторые «акустически прозрачные окна», поэтому реальный интервал углов рассеяния
. Следует также иметь в виду, что доступ ко многим участкам человеческого организма возможен лишь через некоторые «акустически прозрачные окна», поэтому реальный интервал углов рассеяния ![]() и
и ![]() , как правило, ограничен. И наконец, максимальная частота, которая может быть использована при исследовании рассеяния, также ограничена из-за роста затухания звука. Это накладывает определенный предел на пространственное разрешение параметров
, как правило, ограничен. И наконец, максимальная частота, которая может быть использована при исследовании рассеяния, также ограничена из-за роста затухания звука. Это накладывает определенный предел на пространственное разрешение параметров ![]() и
и ![]() . Таким образом, в целом результаты измерения рассеяния позволяют получить ограниченную информацию о
. Таким образом, в целом результаты измерения рассеяния позволяют получить ограниченную информацию о ![]() и
и ![]() . Во многих случаях экспериментальным путем удается определить лишь некий усредненный параметр, такой как сечение рассеяния.
. Во многих случаях экспериментальным путем удается определить лишь некий усредненный параметр, такой как сечение рассеяния.
Если на рассеивающий элемент падает звуковая волна с интенсивностью ![]() (под интенсивностью понимается поток энергии через единичную площадку), то полная рассеянная мощность S будет пропорциональна
(под интенсивностью понимается поток энергии через единичную площадку), то полная рассеянная мощность S будет пропорциональна ![]() . Коэффициент пропорциональности между этими величинами
. Коэффициент пропорциональности между этими величинами ![]() называется полным сечением рассеяния и имеет размерность площади:
называется полным сечением рассеяния и имеет размерность площади:
![]()
Можно ввести также понятие дифференциального сечения рассеяния ![]() . Пусть
. Пусть ![]() — полная мощность, рассеянная в пределах телесного угла
— полная мощность, рассеянная в пределах телесного угла ![]() в направлении
в направлении ![]() , тогда
, тогда
![]()
Частным примером дифференциального сечения рассеяния является сечение обратного рассеяния
![]()
Сечение поглощения определяется как отношение полной мощности, теряемой первичной волной и преобразующейся в тепло в данной локальной области, к плотности потока энергии (интенсивности) в первичной волне
Поглощенная мощность
![]()
Сечение затухания представляет собой относительную величину полной мощности, теряемой первичной волной за счет рассеяния и поглощения:
![]()
Подобные определения различных сечений применимы к произвольному рассеивающему препятствию в однородной плоской волне, причем в равной мере их можно использовать как в случае одиночного препятствия, так и при наличии совокупности рассеивателей. В тех средах, где рассеиватели распределены случайным образом и рассматриваемый объем содержит достаточно большое их число, рассеиваемая мощность будет пропорциональна этому объему, и рассеяние называется некогерентным [20]. В этих случаях эффективность рассеяния на совокупности препятствий можно охарактеризовать с помощью сечения рассеяния на единицу объема. Эта величина называется коэффициентом рассеяния ![]() и имеет размерность м-1. Аналогичным образом можно определить дифференциальный коэффициент рассеяния да, коэффициент обратного рассеяния
и имеет размерность м-1. Аналогичным образом можно определить дифференциальный коэффициент рассеяния да, коэффициент обратного рассеяния ![]() , коэффициент поглощения
, коэффициент поглощения ![]() и коэффициент затухания
и коэффициент затухания ![]() . Следует подчеркнуть, что все эти коэффициенты имеют смысл только в случае некогерентного рассеяния.
. Следует подчеркнуть, что все эти коэффициенты имеют смысл только в случае некогерентного рассеяния.
Пусть на слой некогерентно рассеивающего материала толщиной dx: падает волна с интенсивностью ![]() и площадью поперечного сечения А. При этом полная мощность, теряемая волной при прохождении слоя между х и х+dx, определяется выражением
и площадью поперечного сечения А. При этом полная мощность, теряемая волной при прохождении слоя между х и х+dx, определяется выражением
![]()
Ослабление интенсивности волны есть ![]() откуда
откуда
![]()
Здесь предполагается, что энергия, теряемая первичной волной, не возвращается в нее в результате многократного рассеяния.
Сечение рассеяния можно рассчитать, зная звуковое давление в рассеянной волне.
При экспериментальном исследовании рассеяния наиболее удобно проводить измерения звукового давления в дальнем поле рассеивающего препятствия, где рассеянная волна становится сферической (см. уравнение (6.12)):
![]()
Интенсивность этой волны есть
![]()
откуда поток энергии, теряемой объемом V за счет рассеяния, можно представить в виде

где интегрирование проводится по поверхности S, ограничивающей рассеивающий объем. Подстановка (6.24) в (6.26) дает
![]()
Коэффициент рассеяния определяется последним выражением, нормированным по отношению к интенсивности падающей волны ![]() и рассеивающему объему V:
и рассеивающему объему V:
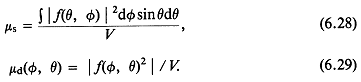
В приближении Борна (см. разд. 6.2.1) полное сечение рассеяния определяется выражением
![]()
До сих пор мы определяли все сечения рассеяния для конкретной ориентации рассеивающего препятствия, задаваемой углами ![]() и
и ![]() . Однако, поскольку сечение рассеяния представляет собой усредненный параметр, то целесообразно провести усреднение по ряду направлений с учетом свойств симметрии препятствия. Так, например, в случае изотропных биологических тканей типа печени мы можем провести усреднение по всем углам:
. Однако, поскольку сечение рассеяния представляет собой усредненный параметр, то целесообразно провести усреднение по ряду направлений с учетом свойств симметрии препятствия. Так, например, в случае изотропных биологических тканей типа печени мы можем провести усреднение по всем углам: ![]()
![]() .
.
Для тканей, обладающих аксиальной симметрией, таких как мышцы, целесообразно определять соответствующие сечения рассеяния отдельно для случая, когда волновой вектор первичной волны параллелен мышечным волокнам, и отдельно для тех ситуаций, когда волновой вектор перпендикулярен волокнам.
Кроме того, можно ввести еще несколько усредненных сечений, которые поддаются экспериментальному измерению. Они будут рассмотрены в разд. 6.4.1.
6.2.3. РЕШЕНИЕ ДЛЯ ОДИНОЧНОГО ПРЕПЯТСТВИЯ
В некоторых случаях, когда рассеивающее препятствие имеет простую геометрическую форму, волновое уравнение можно решить и получить в явном виде выражения для сечения рассеяния. Точное решение для препятствия сферической формы известно как теория Ми [33]. Эта теория совместно с теорией для препятствия цилиндрической формы обстоятельно изложена в гл. 8 книги Морза и Ингарда [38]. Получены также решения для некоторых препятствий других форм, однако с помощью сфер и цилиндров удается аппроксимировать многие типы рассеивающих элементов, характерных для биологических сред. Ниже будет рассмотрено решение для препятствия сферической формы в приближении Борна. Из уравнений (6.12) — (6.15) следует, что
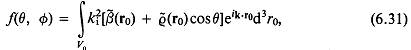
где ![]()
В данном случае удобно ввести сферические координаты, совмещая центр рассеивающей сферы с началом координат и вектор К с направлением оси z. В результате
Вводя ![]() и
и ![]() , получаем
, получаем
В результате интегрирования
![]()
При ![]()
![]()
и при отсутствии флуктуаций плотности рассеяние носит изотропный характер. V — объем рассеивающей сферы, и рассеянная мощность пропорциональна ![]() .
.
На рис. 6.3. для ряда значений ki показаны угловые распределения рассеянной мощности. В данном случае рассеяние имеет когерентный характер, поскольку рассеянная мощность пропорциональна V2, а не V.
Рис. 6.3. Угловые зависимости дифференциального сечения рассеяния для сферы при различных значениях ka (решение в приближении Борна).
6.2.4. ДИФРАКЦИОННАЯ ТЕОРИЯ ДЛЯ СОВОКУПНОСТИ РАССЕИВАТЕЛЕЙ
Если в рассеивающем объеме содержится множество идентичных рассеивателей, то волны, рассеянные на каждом из них, будут интерферировать друг с другом. По этой причине результирующее рассеянное поле будет зависеть от взаимного расположения отдельных рассеивателей. Если в заданном объеме находится N рассеивателей, положение которых определяется векторами ri то функцию распределения для рассеянного поля в пренебрежении многократным рассеянием можно представить в виде
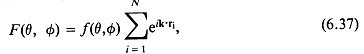
где
![]()
является характеристикой отдельного рассеивателя.
Если предположить, что рассеивающие элементы образуют правильную трехмерную решетку, то
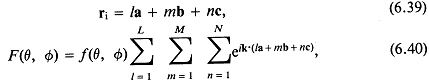
где l, m, n — целые числа, а векторы a, b и с представляют собой векторы трансляции.
Функция распределения F принимает максимальные значения
при условии, что
![]()
Решения уравнения (6.41) можно найти в учебниках по рентгеновской кристаллографии (см., например, работу [22]), где рассматривается обратная задача нахождения векторов a, b и с по известной функции ![]() .
.
На практике трудно измерить функцию распределения ![]() , поскольку для этих целей необходимо использовать два преобразователя (см. также работу Нассири [40]). Проще получить информацию о сечении обратного рассеяния, когда
, поскольку для этих целей необходимо использовать два преобразователя (см. также работу Нассири [40]). Проще получить информацию о сечении обратного рассеяния, когда ![]() и
и ![]() . Николас [43] провел теоретическое и экспериментальное исследование зависимости функции F(
. Николас [43] провел теоретическое и экспериментальное исследование зависимости функции F(![]() ) от ориентации решетки рассеивателей. Он использовал узкую полосу частот при измерениях рассеянного поля. Результаты, полученные Николасом для биологических тканей, будут обсуждаться в разд. 6.4.4. Зависимость обратного рассеяния от частоты и ориентации исследовалась также теоретически Кохом [34], который рассмотрел случай двумерной решетки рассеивателей со случайными возмущениями в ее периодичности.
) от ориентации решетки рассеивателей. Он использовал узкую полосу частот при измерениях рассеянного поля. Результаты, полученные Николасом для биологических тканей, будут обсуждаться в разд. 6.4.4. Зависимость обратного рассеяния от частоты и ориентации исследовалась также теоретически Кохом [34], который рассмотрел случай двумерной решетки рассеивателей со случайными возмущениями в ее периодичности.
Следует отметить, что дифракционные измерения полезны при исследовании совокупностей рассеивателей с геометрически правильным расположением. Следующий раздел посвящен задаче рассеяния в случайно-неоднородных средах.
6.3. РАССЕЯНИЕ В СЛУЧАЙНО-НЕОДНОРОДНЫХ СРЕДАХ
6.3.1. МОДЕЛИ БИОЛОГИЧЕСКИХ ТКАНЕЙ
Биологическая ткань представляет собой сложную среду, акустические свойства которой на микромасштабном уровне пока еще не изучены. Поэтому в настоящее время для исследования рассеивающих свойств биологических тканей обычно используются простые теоретические модели. Хотя некоторые ткани действительно обладают определенной периодичностью структуры, как, например, скелетные мышцы, состоящие из набора цилиндрических фибрилл с гексагональным расположением, ни одна из тканей не имеет идеально правильной структуры. В большинстве случаев структура биологических тканей занимает промежуточное положение между двумя предельными организациями — идеальной периодичностью и совершенно неупорядоченной структурой. Как уже отмечалось, рассеяние на регулярных структурах можно исследовать с помощью дифракционной теории. В данном разделе мы рассмотрим две принципиально различные модели случайно-неоднородных структур.
6.3.2. МОДЕЛЬ ДИСКРЕТНЫХ РАССЕИВАТЕЛЕЙ
В рамках этой модели предполагается, что случайно-неоднородная среда представляет собой набор дискретных рассеивателей (не обязательно идентичных), внедренных случайным образом в однородную подложку. Предполагается также, что размеры каждого рассеивателя малы по сравнению с длиной волны. Суммарное рассеянное поле определяется суперпозицией волн, рассеянных на каждом отдельном рассеивающем элементе. Такой подход был предложен Фолди [20], он ввел также понятия когерентности и некогерентности. При любом фиксированном расположении рассеивателей результирующее рассеяние характеризуется временной когерентностью, но в то же время его можно разделить на пространственно когерентное и некогерентное в соответствии с влиянием каких-либо изменений во взаимном расположении отдельных рассеивателей. Когерентная часть Рс определяется статистическим усреднением по множеству различных конфигураций <Р>, и Фолди показал, что эта величина подчиняется однородному волновому уравнению со скоростью распространения, измененной из-за наличия рассеивателей. Отсюда следует, что когерентная часть не дает вклада в рассеянную волну. Некогерентная часть Pinc обусловлена изменениями пространственных конфигураций рассеивателей, и именно она дает вклад в результирующее рассеянное поле. Таким образом [28],
![]()
причем
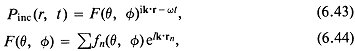
где ![]() и
и ![]() — сечение рассеяния и пространственная координата n-го рассеивателя. Рассеяние на каждом рассеивающем элементе в силу малости его размеров по сравнению с длиной волны можно считать изотропным, при этом из уравнения (6.38) следует, что
— сечение рассеяния и пространственная координата n-го рассеивателя. Рассеяние на каждом рассеивающем элементе в силу малости его размеров по сравнению с длиной волны можно считать изотропным, при этом из уравнения (6.38) следует, что ![]() .
.
Функция ![]() является случайной функцией, для которой статистическое среднее равно нулю. Ее статистические свойства обсуждаются в разд. 6.5, посвященном анализу рассеяния импульсных сигналов. Средняя по ансамблю (некогерентная) интенсивность рассеяния определяется выражением
является случайной функцией, для которой статистическое среднее равно нулю. Ее статистические свойства обсуждаются в разд. 6.5, посвященном анализу рассеяния импульсных сигналов. Средняя по ансамблю (некогерентная) интенсивность рассеяния определяется выражением
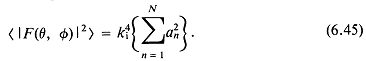
В случае N идентичных рассеивателей
![]()
Таким образом, интенсивность рассеянного поля пропорциональна N и зависимость этой интенсивности от частоты подчиняется закону Рэлея.
6.3.3. МОДЕЛЬ НЕОДНОРОДНОГО КОНТИНУУМА
В данной модели предполагается, что в среде имеют место небольшие флуктуации плотности и сжимаемости относительно постоянных средних значений, причем статистические свойства этих флуктуаций описываются вполне определенной функцией автокорреляции. При этом каждый элемент неоднородной среды становится источником рассеянных волн. Такая модель позволяет рассчитать усредненную интенсивность некогерентного рассеяния. В дальнейшем с целью упрощения математических выкладок мы будем считать, что плотность среды постоянна, и рассмотрим только флуктуации сжимаемости. Последующий анализ базируется на работе Чернова [14].
Из уравнения (6.15) следует, что
![]()
Функции ![]() и
и ![]() являются случайными функциями, поэтому для них необходимо провести статистическое усреднение:
являются случайными функциями, поэтому для них необходимо провести статистическое усреднение:
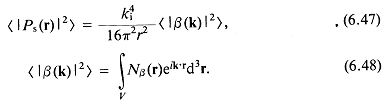
При учете флуктуаций плотности выражение (6.47) значительно усложняется, в нем появляются перекрестные члены, в которые входят плотность и сжимаемость. В этом случае получить аналитическое решение более трудно, хотя в принципе необходимые расчеты аналогичны тем, которые проводились при выводе выражения (6.47).
Величина ![]() представляет собой автокорреляционную функцию для флуктуаций сжимаемости. Хотя могут быть использованы и другие виды этой функции, наиболее часто предполагается, что она имеет гауссову форму:
представляет собой автокорреляционную функцию для флуктуаций сжимаемости. Хотя могут быть использованы и другие виды этой функции, наиболее часто предполагается, что она имеет гауссову форму:
![]()
где ![]() — радиус корреляции.
— радиус корреляции.
Подстановка (6.49) в (6.47) и (6.48) дает
![]()
Анализ этого выражения позволяет сделать несколько выводов. Для мелкомасштабных флуктуаций ![]() рассеяние носит изотропный характер и его интенсивность пропорциональна
рассеяние носит изотропный характер и его интенсивность пропорциональна ![]() . В случае крупномасштабных флуктуаций рассеянное поле характеризуется резко выраженной направленностью в прямом направлении, и большая часть рассеянной мощности сконцентрирована в пределах малого телесного угла:
. В случае крупномасштабных флуктуаций рассеянное поле характеризуется резко выраженной направленностью в прямом направлении, и большая часть рассеянной мощности сконцентрирована в пределах малого телесного угла:
В рамках рассмотренной модели ни при каких значениях ка мощность, рассеянная в обратном направлении, не может превышать мощность, рассеянную в прямом направлении. Другими словами, данная модель непригодна для тех случаев, когда возникает подобная ситуация, и необходимо применять другие модели среды [40]. Учет флуктуаций плотности среды позволил бы создать более универсальную модель. С этой же целью можно использовать более сложную автокорреляционную функцию, которая учитывала бы и анизотропию статистических свойств среды.
6.4. ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ РАССЕЯНИЯ
В разд. 6.2.2 было дано определение основных сечений рассеяния, и одна из задач экспериментального исследования состоит в правильном измерении этих сечений независимо от выбранной методики или используемой аппаратуры. Как было показано, сечение рассеяния зависит не только от угловых координат рассеянной волны ![]() и
и ![]() , но также и от пространственной ориентации исследуемого образца (т. е. от углов
, но также и от пространственной ориентации исследуемого образца (т. е. от углов ![]() и
и ![]() и от частоты. В силу этого можно ввести несколько новых понятий сечения рассеяния на основе статистического усреднения по одному или нескольким из упомянутых углов и затем сопоставить их с той или иной конкретной схемой измерения. Особый интерес представляет измерение сечения обратного рассеяния, усредненного по различным ориентациям исследуемого образца ткани. Это сечение можно определить следующим образом:
и от частоты. В силу этого можно ввести несколько новых понятий сечения рассеяния на основе статистического усреднения по одному или нескольким из упомянутых углов и затем сопоставить их с той или иной конкретной схемой измерения. Особый интерес представляет измерение сечения обратного рассеяния, усредненного по различным ориентациям исследуемого образца ткани. Это сечение можно определить следующим образом:
![]()
При измерении обратного рассеяния используется один преобразователь, в других случаях необходимы два преобразователя. В общем случае в среду излучается акустический импульс, а принятый рассеянный сигнал, полученный в режиме типа А, стробируется таким образом, чтобы рассеивающий объем определялся областью пересечения двух пучков. При этом регистрируемый рассеянный сигнал представляет собой сложную функцию длительностей стробирующего и излучаемого импульсов, а также ширины пучка [41]. Излучаемый акустический сигнал может быть тональным (синусоидальным) или широкополосным импульсом. В последнем случае для определения зависимости рассеянной мощности от частоты необходим спектральный анализ принятого сигнала. В работе [51] рассмотрена возможность применения тональных импульсных сигналов для измерения обратного рассеяния ультразвука с помощью метода замещения, в основе которого лежит сравнение полученных сигналов с сигналами, рассеянными эталонной мишенью, например, плоским отражателем. При попытках провести абсолютные измерения рассеяния необходимо выполнить операцию обращений свертки спектральной характеристики преобразователя и используемой электронной аппаратуры с характеристикой исследуемой ткани по результатам измерений на плоском отражателе. Следует отметить, что во многих работах результаты измерения рассеяния все еще выражаются в децибелах относительно значений, полученных для выбранного плоского отражателя. Отражатель должен быть установлен на том же расстоянии от преобразователя, что и рассеивающий элемент, причем оба они с целью уменьшения погрешностей, связанных с эффектом компенсации фаз, должны находиться в дальнем поле преобразователя.
Существуют два основных источника погрешностей при измерениях рассеяния. Первый из них связан с необходимостью выбора некоторого компромиссного соотношения между пространственным разрешением и разрешением по частоте. Если время стробирования равно т, то пространственное разрешение в случае обратного рассеяния будет определяться величиной ![]() . При этом в результате свертки частотного спектра с функцией
. При этом в результате свертки частотного спектра с функцией ![]() разрешение по частоте будет ограничено величиной
разрешение по частоте будет ограничено величиной ![]() . Второй источник погрешностей возникает из-за компенсации фаз на приемном преобразователе (разд. 3.2). Сечение рассеяния обычно выражается через интенсивность рассеянных волн, тогда как большинство пьезоэлектрических преобразователей являются фазочувствительными элементами. Любые флуктуации фазы сигнала по площади приемного преобразователя будут приводить к заниженным оценкам интенсивности принятого сигнала и соответственно сечения рассеяния. Уменьшить влияние этого эффекта можно, проводя измерения в «дальнем поле» рассеивающего объема, где рассеянные волны являются приблизительно сферическими, а в пределах небольшой апертуры их можно считать плоскими (из-за малой кривизны волновых фронтов). Погрешность будет уменьшаться при использовании приемных преобразователей малых размеров (например, гидрофонов) или фазонечувствительного преобразователя [13], хотя такое решение не очень подходит для измерения обратного рассеяния. Отметим, что эффект компенсации фаз является более серьезным источником погрешностей при измерениях затухания, о чем шла речь в гл. 4.
. Второй источник погрешностей возникает из-за компенсации фаз на приемном преобразователе (разд. 3.2). Сечение рассеяния обычно выражается через интенсивность рассеянных волн, тогда как большинство пьезоэлектрических преобразователей являются фазочувствительными элементами. Любые флуктуации фазы сигнала по площади приемного преобразователя будут приводить к заниженным оценкам интенсивности принятого сигнала и соответственно сечения рассеяния. Уменьшить влияние этого эффекта можно, проводя измерения в «дальнем поле» рассеивающего объема, где рассеянные волны являются приблизительно сферическими, а в пределах небольшой апертуры их можно считать плоскими (из-за малой кривизны волновых фронтов). Погрешность будет уменьшаться при использовании приемных преобразователей малых размеров (например, гидрофонов) или фазонечувствительного преобразователя [13], хотя такое решение не очень подходит для измерения обратного рассеяния. Отметим, что эффект компенсации фаз является более серьезным источником погрешностей при измерениях затухания, о чем шла речь в гл. 4.
Дополнительный источник погрешности может быть связан с затуханием звука как в самой рассеивающей области, так и в вышележащих тканях. В определенной степени эту погрешность можно учесть, если известна величина затухания [51]. При этом необходимо обращать внимание на характер рассеяния в прямом направлении. На практике большие трудности при исследовании рассеивающих свойств среды возникают из-за наличия в тканях газовых пузырьков, являющихся чрезвычайно эффективными рассеивателями ультразвуковых волн. Поэтому предварительно необходимо удалить эти пузырьки из исследуемого образца ткани. Более подробно анализ возможных источников ошибок при измерениях рассеяния выполнен в работе Нассири и Хилла [41].
Ниже мы рассмотрим некоторые специфические особенности рассеяния в биологических тканях и остановимся на тех выводах, которые можно сделать, исходя из результатов измерения сечения рассеяния в этих тканях.
6.4.2. ВЗАИМОСВЯЗЬ МЕЖДУ ПОЛНЫМ СЕЧЕНИЕМ РАССЕЯНИЯ И ЗАТУХАНИЕМ
В разд. 6.2.2 было показано, что затухание звука обусловлено двумя причинами — переизлучением или рассеянием энергии первичной волны, а также ее поглощением и преобразованием в тепло. Интересно было бы оценить относительные вклады двух этих механизмов, хотя для подобных оценок имеется очень мало экспериментальных данных. В принципе на основе выражения (6.23) экспериментальным путем можно определить величину полного затухания и на практике подобные измерения проводились с точностью около 10%. Однако измерения полного сечения рассеяния или сечения поглощения вызывают большие затруднения.
Можно привести очень мало результатов прямых измерений полного сечения рассеяния. Грамиак и др. [25], а также Нассири и Хилл [41] сообщали о методах измерения зависимости дифференциального сечения от угла рассеяния. Трудность использования полученных этими авторами результатов для оценки полного сечения рассеяния заключается в том, что в большинстве экспериментальных схем прямое рассеяние не удается измерить для углов, меньших 60°. Поэтому прямое рассеяние определяется путем экстраполяции экспериментальных данных, и результаты оценки полного сечения будут зависеть от этой экстраполяции. В ряде случаев эксперименты показали, что прямое рассеяние велико — в результате возникает большая погрешность при оценке полного сечения рассеяния. Данная ситуация усложняется еще больше из-за необходимости введения поправок, учитывающих изменения самого рассеивающего объема. Нассири на основе предварительных данных пришел к выводу, что для ряда тканей отношение ![]() может превышать 20, т. е. оно больше значения 4
может превышать 20, т. е. оно больше значения 4![]() , полученного в случае изотропного рассеяния. Еще одним источником погрешности является разброс в измеренных значениях
, полученного в случае изотропного рассеяния. Еще одним источником погрешности является разброс в измеренных значениях ![]() и
и ![]() . По этой причине имеющиеся данные позволили лишь прийти к заключению, что отношение
. По этой причине имеющиеся данные позволили лишь прийти к заключению, что отношение ![]() не должно превышать 40% на частоте 1 МГц, а более точные оценки были невозможны.
не должно превышать 40% на частоте 1 МГц, а более точные оценки были невозможны.
Значительно проще экспериментальным путем определить сечение обратного рассеяния. Кроме того, можно найти взаимосвязь между коэффициентом рассеяния и коэффициентом затухания, регистрируя изменения величин ![]() и
и ![]() в результате тех или иных видоизменений биологической ткани. При этом предполагается, что поглощение и угловое распределение рассеяния не меняются при подобных модификациях ткани. Другими словами,
в результате тех или иных видоизменений биологической ткани. При этом предполагается, что поглощение и угловое распределение рассеяния не меняются при подобных модификациях ткани. Другими словами, ![]() , откуда
, откуда
![]()
Бэмбер [4] использовал для указанных целей изменение тканей при автолизе. Им было получено, что при автолизе коэффициент обратного рассеяния быстро спадал во времени, уменьшаясь на 95%, тогда как коэффициент затухания уменьшался менее чем на 15%. В результате это давало ![]() < 16%. Исследовалось также влияние температуры и фиксации тканей [6], однако эти изменения, по всей видимости, приводят и к изменению коэффициента поглощения. Паули и Шван [46] экспериментально исследовали зависимость коэффициента затухания от процесса гомогенизации печени, в результате которого из ткани удаляется большая часть рассеивающих структурных элементов. И в этом случае оценки показывают, что значение отношения
< 16%. Исследовалось также влияние температуры и фиксации тканей [6], однако эти изменения, по всей видимости, приводят и к изменению коэффициента поглощения. Паули и Шван [46] экспериментально исследовали зависимость коэффициента затухания от процесса гомогенизации печени, в результате которого из ткани удаляется большая часть рассеивающих структурных элементов. И в этом случае оценки показывают, что значение отношения ![]() должно лежать в интервале 10—20% [27].
должно лежать в интервале 10—20% [27].
Полхаммер и О'Брайен [47] измерили полное сечение рассеяния как разность между коэффициентами затухания и поглощения. Следует отметить, что такой метод страдает большой неточностью из-за погрешностей измерения коэффициентов затухания и поглощения.
Подводя итог, можно сказать, что существующие методы оценки полного сечения рассеяния пока не удовлетворяют предъявляемым к ним требованиям. Они не позволяют получить точное значение отношения ![]() по имеющимся экспериментальным данным.
по имеющимся экспериментальным данным.
Кровь представляет собой единственную биологическую среду, для которой получено сравнительно много экспериментальных данных по рассеянию. В силу того, что размеры красных кровяных телец много меньше длины ультразвуковой волны, эти элементы можно рассматривать приближенно как сферы с одинаковым объемом. В работе [2] в этом приближении получено выражение для сечения рассеяния красных кровяных телец, учитывающее влияние вязкости; оказалось, что сечение рассеяния должно быть намного меньше сечения вязкого поглощения. Шанг и др. [49] исследовали влияние гематокрита на рассеивающие свойства крови. Было установлено, что сечение рассеяния на частицу остается неизменным при показателе гематокрита, меньшем 8%, и начинает уменьшаться при более высоких значениях этого показателя. Эти данные свидетельствуют о том, что в таких случаях определенную роль может играть многократное рассеяние. Как показано в работе [3], экспериментально найденные для крови значения сечения рассеяния хорошо согласуются с результатами теоретических расчетов; кроме того, зависимость рассеяния от частоты имеет рэлеевский характер. В своей более поздней работе [50] Шанг и др. измерили дифференциальное сечение рассеяния и показали, что по сравнению с теорией Морза и Ингарда [38], не учитывающей вязкость среды, теория, развитая в работе [2], лучше соответствует экспериментальным данным. Хорошее согласие между теорией и экспериментом в данном случае обусловлено простотой двухфазной структуры крови, которая достаточно точно описывается с помощью простых теоретических моделей. Другие биологические ткани имеют значительно более сложную структуру, и подобный анализ для них пока не проводился.
6.4.3. ЗАВИСИМОСТЬ СЕЧЕНИЯ РАССЕЯНИЯ ОТ ЧАСТОТЫ
В разд. 6.3.3 было показано, что частотная зависимость рассеяния определяется отношением радиуса корреляции среды ![]() к длине волны. При малых значениях
к длине волны. При малых значениях ![]() сечение рассеяния пропорционально f4 при больших значениях
сечение рассеяния пропорционально f4 при больших значениях ![]() зависимость полного сечения рассеяния от частоты переходит в квадратичную зависимость (f2), тогда как сечение обратного рассеяния уменьшается как
зависимость полного сечения рассеяния от частоты переходит в квадратичную зависимость (f2), тогда как сечение обратного рассеяния уменьшается как ![]() . Таким образом, если среда характеризуется единственным радиусом корреляции
. Таким образом, если среда характеризуется единственным радиусом корреляции ![]() , то зависимость сечения обратного рассеяния от частоты носит сложный характер:
, то зависимость сечения обратного рассеяния от частоты носит сложный характер: ![]() . Если представить эту зависимость в двойном логарифмическом масштабе, то можно ожидать, что при повышении частоты наклон кривой, т. е. параметр m, будет уменьшаться (рис. 6.4, а).
. Если представить эту зависимость в двойном логарифмическом масштабе, то можно ожидать, что при повышении частоты наклон кривой, т. е. параметр m, будет уменьшаться (рис. 6.4, а).
Частотную зависимость сечения обратного рассеяния для печени исследовали разные авторы. Все они пришли к одинаковому выводу, что параметр m монотонно возрастает при повышении частоты от m = 0 на частоте 1 МГц до m = 3 на частоте 10 МГц [4, 5] (рис. 6.4, а). Этот результат свидетельствует о том, что в случае печени простейшая модель с единственной длиной корреляции становится непригодной. Для описания рассеивающих свойств печени необходимо использовать более сложные, комбинированные модели с двумя или тремя различными радиусами корреляции. В частности, клетки печени с размерами 20 мкм и дольки печени с размерами около 1 мм представляют собой структуры, характеризующиеся различными радиусами корреляции ![]() . Учет этих различий позволяет получить требуемую частотную зивисимость, а учет более крупных неоднородностей типа кровеносных сосудов дает, кроме того, более точную аппроксимацию экспериментальных данных на низких частотах. Это один из многих подходов, позволяющих получить правильную частотную зависимость. На рис. 6.4, б показана одна из моделей с тремя радиусами корреляции. Как можно видеть, обоснованный выбор трех различных радиусов корреляции и среднеквадратических значений амплитуд (величины
. Учет этих различий позволяет получить требуемую частотную зивисимость, а учет более крупных неоднородностей типа кровеносных сосудов дает, кроме того, более точную аппроксимацию экспериментальных данных на низких частотах. Это один из многих подходов, позволяющих получить правильную частотную зависимость. На рис. 6.4, б показана одна из моделей с тремя радиусами корреляции. Как можно видеть, обоснованный выбор трех различных радиусов корреляции и среднеквадратических значений амплитуд (величины ![]() и <
и <![]() >2 в уравнении (6.50)) обеспечивает получение такой частотной зависимости рассеяния, которая хорошо согласуется с экспериментальными данными. Следует отметить, что и другие модели дают хорошую аппроксимацию экспериментальных результатов. В частности, Николас [44] показал, что использование двухчленной экспоненциальной автокорреляционной функции дает лучшее описание полученных им экспериментальных данных по сравнению с гауссовой автокорреляционной функцией, имеющей тот же радиус корреляции. В этой работе обсуждаются также и другие модели.
>2 в уравнении (6.50)) обеспечивает получение такой частотной зависимости рассеяния, которая хорошо согласуется с экспериментальными данными. Следует отметить, что и другие модели дают хорошую аппроксимацию экспериментальных результатов. В частности, Николас [44] показал, что использование двухчленной экспоненциальной автокорреляционной функции дает лучшее описание полученных им экспериментальных данных по сравнению с гауссовой автокорреляционной функцией, имеющей тот же радиус корреляции. В этой работе обсуждаются также и другие модели.
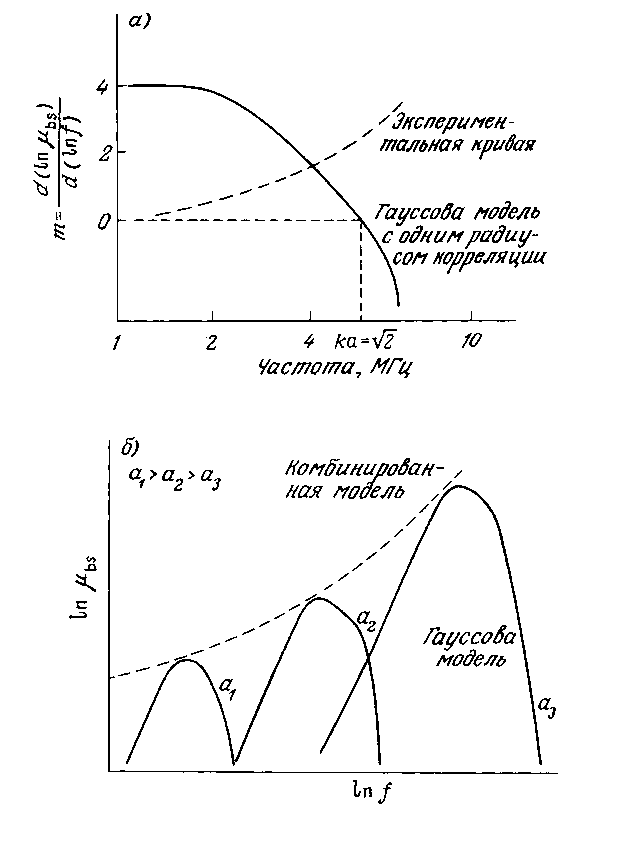
Рис. 6.4. Частотная зависимость обратного рассеяния в модели неоднородного континуума: а — степенная зависимость сечения обратного рассеяния от частоты; показаны экспериментальные результаты и результаты расчета для ткани с гауссовой автокорреляционной функцией; б — частотная зависимость сечения обратного рассеяния, рассчитанная для гипотетической комбинированной модели с тремя характерными размерами структуры.
В принципе в спектре рассеяния можно подавить усредненную компоненту и исследовать оставшиеся флуктуации. Периодичность в спектре рассеяния можно проанализировать с помощью различных методов, включая кепстральный и корреляционный анализ [30]. Нетрудно показать, что периодичность в частотном спектре рассеяния обусловлена наличием в среде регулярных рассеивающих структур, и такая периодичность действительно наблюдалась в спектрах, полученных для сетчатки глаза [36] (см. также гл. 10) и печени [31]. Существуют, однако, данные, что подобная периодичность в частотных спектрах характерна лишь для очень регулярных структур [34]; в спектрах рассеяния от совершенно неупорядоченных структур будут наблюдаться флуктуации, величина которых зависит главным образом от ширины полосы зондирующего акустического импульса.
6.4.4. УГЛОВАЯ ЗАВИСИМОСТЬ КОЭФФИЦИЕНТОВ РАССЕЯНИЯ
Зависимость коэффициента обратного рассеяния от пространственной ориентации образца печени относительно первичной волны ![]() исследовалась Николасом [43]. Он обнаружил у печени периодичность, характерную для квазирегулярной структуры с периодом порядка 1 мм; кроме того, было установлено, что угловая зависимость коэффициента рассеяния для печени в патологии отличается от аналогичной зависимости для нормальной печени [55]. Нассири и Хилл [42] исследовали угловую зависимость рассеяния для трех различных биологических сред — печени, скелетной мышцы и крови. Эти авторы пришли к заключению, что характерный масштаб структур, ответственных за рассеяние в каждом из этих случаев, составляет 55, 74 и 6,0 мкм. Было также показано, что относительная величина пространственных вариаций плотности в этих тканях сравнима с флуктуациями сжимаемости. Отсюда следует, что для правильного понимания характера рассеяния необходимо учитывать пространственные флуктуации не только сжимаемости, но и плотности.
исследовалась Николасом [43]. Он обнаружил у печени периодичность, характерную для квазирегулярной структуры с периодом порядка 1 мм; кроме того, было установлено, что угловая зависимость коэффициента рассеяния для печени в патологии отличается от аналогичной зависимости для нормальной печени [55]. Нассири и Хилл [42] исследовали угловую зависимость рассеяния для трех различных биологических сред — печени, скелетной мышцы и крови. Эти авторы пришли к заключению, что характерный масштаб структур, ответственных за рассеяние в каждом из этих случаев, составляет 55, 74 и 6,0 мкм. Было также показано, что относительная величина пространственных вариаций плотности в этих тканях сравнима с флуктуациями сжимаемости. Отсюда следует, что для правильного понимания характера рассеяния необходимо учитывать пространственные флуктуации не только сжимаемости, но и плотности.
В целом, анализируя частотную и угловую зависимости рассеяния, можно получить информацию о тех структурных неоднородностях, на которых происходит рассеяние ультразвуковых волн. Основная масса экспериментальных исследований была выполнена на печени, причем результаты этих работ позволили сделать вывод, что за рассеяние5 отвечает ряд структур. Главная цель фундаментальных исследований рассеяния — получить полное представление о структурной организации биологической ткани на основе анализа рассеянных волн, а также выявить и определить местоположения тех или иных нарушений структуры при патологии. На пути достижения этой цели предстоит еще серьезная и кропотливая работа. Имеющиеся экспериментальные данные были получены для частотного диапазона 1-10 МГц. В этом диапазоне можно получить информацию лишь о структурах, характерные размеры которых сравнимы с соответствующими длинами волн, поэтому для более полного анализа рассеяния необходимо расширить полосу частот.
6.4.5. ВЛИЯНИЕ РАЗЛИЧНЫХ КОМПОНЕНТОВ ТКАНЕЙ
В клинической практике не всегда возникает необходимость в получении исчерпывающей информации о размерах и пространственном расположении рассеивающих структур обследуемой ткани. Часто для постановки диагноза достаточно воспользоваться эмпирически найденной связью между сечением рассеяния и компонентами ткани. В ряде работ исследовалась зависимость рассеивающих свойств тканей от относительного содержания различных компонентов и от патологий ткани. Так, например, Фриз и Лайонс [21] получили хорошую корреляцию между обратным рассеянием и процентным содержанием жировой компоненты в печени. Такой результат не удивителен, если учесть специфику распространения звука в жировой ткани (см. гл. 5). Бэмбер с соавт. [9] обнаружили сильную отрицательную корреляцию между рассеивающими свойствами печени человека и процентным содержанием в ней воды. Можно считать, что присутствие воды снижает относительное содержание других структурных компонентов ткани. Этот результат является наглядным примером сложной взаимосвязи различных компонентов ткани в плане их влияния на величину коэффициента обратного рассеяния. Этот вопрос также обсуждается в указанной работе. Часто высказывалось предположение, что основной вклад в рассеяние дает содержащийся в ткани коллаген, хотя экспериментальные данные, подтверждающие это утверждение, стали появляться только в последнее время [47].
Еще меньше внимания уделялось исследованию зависимостей коэффициентов рассеяния от тех или иных патологий ткани, хотя именно рассеяние определяет работу диагностической аппаратуры на принципе В-сканирования. Полученные к настоящему времени данные свидетельствуют о том, что (по крайней мере в печени) рассеяние ультразвука в твердых опухолях слабее, а в ткани с диффузными патологиями сильнее, чем в нормальной ткани [8]. И все же из-за значительного разброса полученных данных окончательные выводы делать рано — требуется проведение дальнейших исследований.
Таким образом, на основе анализа рассеивающих свойств среды можно составить представление лишь о характерных размерах рассеивающих структур и о влиянии тех или иных компонентов ткани на рассеяние. Учесть влияние пространственной конфигурации отдельных структурных компонентов ткани на ее рассеивающие свойства пока еще невозможно.
6.5. РАССЕЯНИЕ ИМПУЛЬСНЫХ СИГНАЛОВ
До сих пор мы рассматривали рассеяние монохроматических пучков, но они не позволяют получить какое-либо пространственное разрешение. В медицинской акустике, однако, широкое применение нашли эхо-импульсные В-сканеры, в которых используются широкополосные импульсы и регистрируется время прихода эхо-сигнала. Данный раздел посвящен анализу теории обратного рассеяния и параметров рассеянных импульсных сигналов, получаемых при использовании стандартной эхо-импульсной аппаратуры.
6.5.1. ОСНОВЫ ТЕОРИИ: ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ТКАНИ
Если известно решение для падающей монохроматической волны, то в принципе решение для широкополосного импульса конечной спектральной ширины может быть получено на основе суперпозиции соответствующих компонент фурье-спектра. Принятый здесь подход аналогичен подходу Гора и Лимана [24], за исключением того, что решение в данном случае ищется во временной области и учитывается влияние приемного преобразователя.
Как было показано, давление в рассеянной волне определяется уравнением (6.8а), которое можно представить в виде
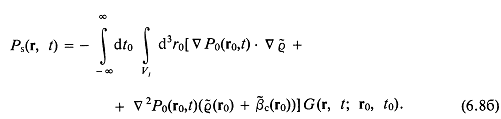
Результирующий принятый сигнал V(t) (сигнал А-эхограммы) определяется интегрированием давления волны, рассеянной в обратном направлении, по поверхности преобразователя S(r). Для удобства поместим начало координат на поверхности преобразователя (рис. 6.5). Таким образом,
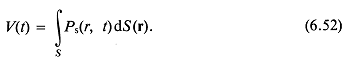
Давление в падающей (первичной) волне, излучаемой тем же преобразователем, определяется следующим выражением [53]:
![]()
где A(f) — функция возбуждения плоского поршневого излучателя, установленного в бесконечном экране. Подстановка (6.86) и (6.53) в (6.52) дает
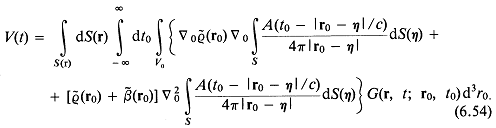
Полученное выражение представляет собой сумму двух слагаемых, каждое из которых следует рассмотреть отдельно.
Подстановка функции Грина в первое слагаемое и интегрирование по to дают
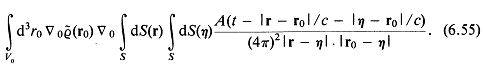

Рис. 6.5. Конфигурация, используемая в расчетах для эхо-импульсных сигналов (разд. 6.5.1).
В этом выражении интеграл
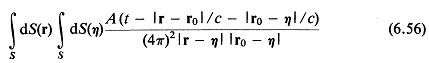
представляет собой импульсную характеристику для точечного отражателя, установленного в точке r0, и его можно выразить в виде
![]()
где символ ![]() обозначает операцию свертки по t и
обозначает операцию свертки по t и
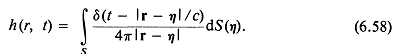
В дальней зоне функцию q (г, /) можно аппроксимировать величиной
![]() и выражение (6.55) преобразовать к виду
и выражение (6.55) преобразовать к виду
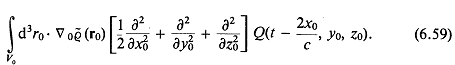
Выполняя интегрирование по частям, получаем
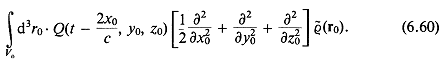
Выполнение аналогичной процедуры для второго слагаемого выражения (6.54) дает
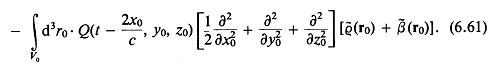
Объединяя оба слагаемых, получаем
![]()
где
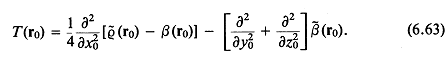
Изображение, формируемое сигналами обратного рассеяния, или В-изображение, получается из множества А-эхограмм посредством сканирования преобразователем. При простом линейном сканировании ось преобразователя остается параллельной координатной оси х, а сам преобразователь перемещается по плоскости (0, у, z). В этом случае сигнал, формирующий Л-эхограммы, определяется выражением
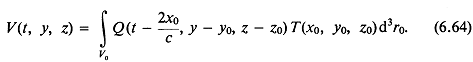
Для перехода от электрического напряжения, снимаемого с преобразователя в А-режиме, к амплитуде визуализируемого сигнала используется следующее преобразование:
![]()
Это дает
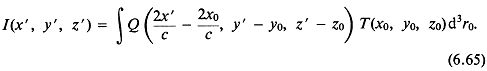
И наконец, реальная А-эхограмма формируется в результате частотной демодуляции высокочастотного сигнала путем детектирования и сглаживающей фильтрации:
![]()
где F — отклик применяемого фильтра низких частот.
Полученные результаты, выраженные формулами (6.62) и (6.63), имеют важное значение. Они показывают, что недетектированный сигнал при В-сканировании определяется сверткой эхо-импульсной характеристики преобразователя и импульсной характеристики ткани T(r0). Отсюда следует, что результаты общей теории формирования изображений, а также методы повышения качества изображений можно использовать применительно к акустическим изображениям, получаемым при В-сканировании. Кроме того, в самих акустических изображениях заложена информация о фундаментальных акустических параметрах исследуемой ткани.
В выражение для импульсной характеристики ткани Т входят производные второго порядка от акустических параметров этой ткани, а также члены, описывающие вариации сжимаемости в направлении, перпендикулярном направлению распространения (например, ![]() ). Наличие этих членов соответствует рассеянию под углом 90°, обусловленному градиентом давления в направлении, перпендикулярном оси преобразователя. При конечной ширине ультразвукового пучка на его границах действительно возникает градиент давления в перпендикулярном направлении, хотя его величина мала по сравнению с градиентами давления в осевом направлении. Для плотности подобный член отсутствует, поскольку рассеяние на флуктуациях плотности имеет дипольный характер и в нем отсутствует компонента под углом 90°. В противоположность этому на флуктуациях сжимаемости происходит рассеяние монопольного типа.
). Наличие этих членов соответствует рассеянию под углом 90°, обусловленному градиентом давления в направлении, перпендикулярном оси преобразователя. При конечной ширине ультразвукового пучка на его границах действительно возникает градиент давления в перпендикулярном направлении, хотя его величина мала по сравнению с градиентами давления в осевом направлении. Для плотности подобный член отсутствует, поскольку рассеяние на флуктуациях плотности имеет дипольный характер и в нем отсутствует компонента под углом 90°. В противоположность этому на флуктуациях сжимаемости происходит рассеяние монопольного типа.
6.5.2. СВОЙСТВА ИЗОБРАЖЕНИЙ, ПОЛУЧАЕМЫХ ПРИ В-СКАНИРОВАНИИ
Выражение, полученное в предыдущем разделе для сигналов, формирующих акустическое изображение при В-сканировании, позволяет рассчитать характеристики этого изображения при известной импульсной характеристике ткани. Обратная задача значительно более трудна, и в некоторых случаях ее решение невозможно. Один из возможных подходов к решению этой проблемы заключается в последовательном использовании различных импульсных характеристик ткани и сравнении смоделированных на компьютере изображений с реальным изображением, полученным при В-сканировании. Такой подход использовали Бэмбер и Дикинсон [7].
В задачах компьютерного моделирования обычно используются две простые модели среды, о которых уже говорилось в разд. 6.3. В рамках модели дискретных рассеивателей импульсная характеристика среды Т(r) определяется выражением
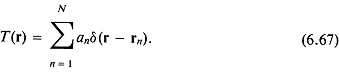
При этом продетектированный сигнал при В-сканировании будет характеризоваться амплитудой
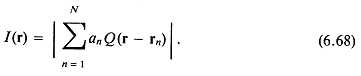
Если спектр первичного импульса сосредоточен в узкой полосе частот, то ![]() где А — огибающая импульса и k0 соответствует центральной частоте спектра. В любой точке амплитуда эхо-сигнала, формирующего А-эхограмму, будет случайной функцией, определяемой конкретным расположением рассеивателей в пределах элемента разрешения А (r):
где А — огибающая импульса и k0 соответствует центральной частоте спектра. В любой точке амплитуда эхо-сигнала, формирующего А-эхограмму, будет случайной функцией, определяемой конкретным расположением рассеивателей в пределах элемента разрешения А (r):
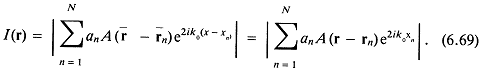
Это выражение аналогично выражению, описывающему спекл-структуру лазерного излучения. Свойства этой структуры исследовал Гудмен [23]. Спекл-структура возникает в тех случаях, когда на шероховатую поверхность падает когерентное лазерное излучение или когерентное излучение другой природы. При этом отдельные рассеиватели пространственно не разрешаются, однако интерференция рассеянных ими волн приводит к случайным флуктуациям результирующей интенсивности с высоким контрастом. Если та же самая поверхность освещается некогерентным световым пучком, то рассеянные волны складываются по интенсивности, что в результате усреднения приводит к низкому среднему контрасту. Аналогичная ситуация возникает и в случае ультразвуковых волн, когда отдельные рассеиватели не разрешаются, но из-за высокой когерентности ультразвукового излучения рассеянные волны интерферируют друг с другом, в результате чего возникают пространственные флуктуации интенсивности рассеяния. В первом приближении статистические свойства амплитуды описываются рэлеевской функцией распределения вероятности [12]:
![]()
Во втором приближении статистические свойства изображений можно исследовать, анализируя спектр мощности эхо-сигнала, амплитуда которого определяется выражением (6.69):
![]()
В данном случае спектр мощности и соответственно пространственная автокорреляционная функция определяются только протяженностью исходного импульса и не зависят от расположения рассеивателей, поскольку эти рассеиватели распределены по пространству случайным образом и их число достаточно велико.
На рис. 6.6 показаны модель дискретных рассеивателей и соответствующее В-изображение, смоделированное на основе цифрового преобразования выражения (6.65). Как можно видеть, структура полученного изображения имеет мало общего с исходной моделью. Однако, хотя исходная структура и не разрешается в изображении, необходимо отметить полученный высокий контраст. Из анализа гистограммы амплитуд следует, что распределение амплитуд в изображении подчиняется рэлеевскому закону, при этом отношение среднеквадратического отклонения к среднему значению равно 2. Мы еще вернемся к обсуждению этих свойств после рассмотрения модели неоднородного континуума.
При анализе модели неоднородного континуума с целью упрощения расчетных выражений мы вновь будем считать, что плотность среды постоянна, а сжимаемость описывается случайной функцией пространственных координат с вполне определенной автокорреляционной функцией. В данном случае автокорреляционная функция имеет гауссову форму ![]() . При этом в соответствии с уравнением (6.63) импульсная характеристика среды определяется второй производной сжимаемости. На рис. 6.7 показаны модель случайно-неоднородной среды и смоделированное на ее основе В-изображение. Видно, что по своему характеру полученное изобра жение аналогично изображению, смоделированному на основе модели дискретных рассеивателей. Сопоставить обе модели можно следующим образом.
. При этом в соответствии с уравнением (6.63) импульсная характеристика среды определяется второй производной сжимаемости. На рис. 6.7 показаны модель случайно-неоднородной среды и смоделированное на ее основе В-изображение. Видно, что по своему характеру полученное изобра жение аналогично изображению, смоделированному на основе модели дискретных рассеивателей. Сопоставить обе модели можно следующим образом.

Рис. 6.6. Компьютерное моделирование В-изображения с использованием модели дискретных рассеивателей: а — фотография рассеивающего объекта (модель дискретных рассеивателей). Среднее расстояние между рассеивателями соответствует 8 элементам изображения, формат изображения 128х128 элементов; б—смоделированное В-изображение рассеивающего объекта; длина волны равна 6 элементам, протяженность импульса — 8 элементам, ширина пучка—12 элементам.
Рис. 6.7. Компьютерное моделирование В-изображения с использованием модели неоднородного континуума: а — фотография рассеивающего объекта (модель неоднородного континуума с гауссовой автокорреляционной функцией; (радиус корреляции равен 6 элементам); б — смоделированное В-изображение рассеивающего объекта (параметры импульса такие же, как на рис. 6.6, б).
Пусть импульсная характеристика среды T(r) представляет собой случайную величину и ее автокорреляционная функция есть ![]() . Пространственный спектр мощности определяется как
. Пространственный спектр мощности определяется как ![]() где F — оператор фурье-преобразования. Отсюда
где F — оператор фурье-преобразования. Отсюда
![]()
где ![]() — случайная величина, равномерно распределенная между 0 и 2
— случайная величина, равномерно распределенная между 0 и 2![]() .
.
Свойства изображения, полученного в рамках такой модели, можно определить на основе анализа спектра мощности. Объединение (6.72) и (6.65) дает
![]()
и
![]()
Если ширина автокорреляционной функции мала по сравнению с длиной волны ультразвука и протяженностью импульса, то ![]() . Сравнение этого выражения с выражением (6.71) показывает, что пространственные структуры изображений в обоих случаях идентичны. Таким образом, при малых радиусах корреляции модель неоднородного континуума позволяет получить изображения, свойства которых аналогичны свойствам изображений, смоделированных в рамках представления о дискретных рассе-ивателях. Модель неоднородного континуума можно использовать для моделирования целого ряда различных ситуаций.
. Сравнение этого выражения с выражением (6.71) показывает, что пространственные структуры изображений в обоих случаях идентичны. Таким образом, при малых радиусах корреляции модель неоднородного континуума позволяет получить изображения, свойства которых аналогичны свойствам изображений, смоделированных в рамках представления о дискретных рассе-ивателях. Модель неоднородного континуума можно использовать для моделирования целого ряда различных ситуаций.
Свойства компьютерных В-изображений, полученных в рамках данной модели, исследовал Дикинсон [17]. Он показал, что при малых значениях ![]() структура этих изображений действительно очень похожа на спекл-структуру когерентного лазерного излучения. В связи с этим можно отметить несколько интересных моментов, возникающих при формировании изображений ткани. Если ткань имеет случайно-неоднородную структуру, характеризующуюся малым радиусом корреляции, то ее статистические свойства как первого, так и второго порядка не зависят от структуры ткани. Статистические параметры первого порядка определяются рэлеевским распределением, во втором порядке они зависят от характеристик исходного импульса. Эксперименты по зрительному восприятию позволяют предположить, что зрительная система человека реагирует именно на статистические характеристики изображения первого и второго порядка [32]. Кроме того, хотя некоторые структурные элементы ткани не могут быть разрешены в изображении, это не играет существенной роли, поскольку изображение характеризуется высококонтрастным шумом, который маскирует любую другую информацию в изображении (см. гл. 7). Расчеты показывают, что отношение сигнала (определяемого как средний уровень отраженного или рассеянного сигнала) к шуму (определяемому как среднеквадратическое отклонение в спекл-структуре) будет константой, равной 2 [12], и малые отклонения от среднего уровня рассеяния подавляются в изображении шумом. Эти свойства В-изображений означают, что визуализация амплитуды эхо-сигналов не является наилучшим способом отображения информации, содержащейся в ультразвуковых эхо-сигналах. Конечно, крупномасштабные структуры биологической ткани будут вопроизводиться в изображении, получаемом в режиме типа В. Однако применительно к мелкомасштабным структурам, которые как раз и дают вклад в полутоновую текстуру изображения, определенные операции обработки эхо-сигналов могли бы повысить информативность получаемых изображений. Эбботт и Тэрстон [1] специально исследовали свойства спекл-структуры в поисках способов ее подавления. С этой целью они совмещали несколько некоррелированных В-изображений, полученных при изменении пространственного положения или частоты ультразвука.
структура этих изображений действительно очень похожа на спекл-структуру когерентного лазерного излучения. В связи с этим можно отметить несколько интересных моментов, возникающих при формировании изображений ткани. Если ткань имеет случайно-неоднородную структуру, характеризующуюся малым радиусом корреляции, то ее статистические свойства как первого, так и второго порядка не зависят от структуры ткани. Статистические параметры первого порядка определяются рэлеевским распределением, во втором порядке они зависят от характеристик исходного импульса. Эксперименты по зрительному восприятию позволяют предположить, что зрительная система человека реагирует именно на статистические характеристики изображения первого и второго порядка [32]. Кроме того, хотя некоторые структурные элементы ткани не могут быть разрешены в изображении, это не играет существенной роли, поскольку изображение характеризуется высококонтрастным шумом, который маскирует любую другую информацию в изображении (см. гл. 7). Расчеты показывают, что отношение сигнала (определяемого как средний уровень отраженного или рассеянного сигнала) к шуму (определяемому как среднеквадратическое отклонение в спекл-структуре) будет константой, равной 2 [12], и малые отклонения от среднего уровня рассеяния подавляются в изображении шумом. Эти свойства В-изображений означают, что визуализация амплитуды эхо-сигналов не является наилучшим способом отображения информации, содержащейся в ультразвуковых эхо-сигналах. Конечно, крупномасштабные структуры биологической ткани будут вопроизводиться в изображении, получаемом в режиме типа В. Однако применительно к мелкомасштабным структурам, которые как раз и дают вклад в полутоновую текстуру изображения, определенные операции обработки эхо-сигналов могли бы повысить информативность получаемых изображений. Эбботт и Тэрстон [1] специально исследовали свойства спекл-структуры в поисках способов ее подавления. С этой целью они совмещали несколько некоррелированных В-изображений, полученных при изменении пространственного положения или частоты ультразвука.
6.5.3. ПРОСТРАНСТВЕННО-ВРЕМЕННАЯ КОРРЕЛЯЦИЯ ЭХО-СИГНАЛОВ
Экспериментальному исследованию характеристик эхо-сигналов, отраженных от участков однородной ткани и совокупностей рассеивателей малого размера, было посвящено несколько работ. Бурк-хардт [12] измерял отношения сигнала к шуму в спекл-структуре В-изображений и исследовал влияние операции логарифмического сжатия на это отношение. Бичем [10] провел аналогичное исследование рассеяния акустических волн в металлах. Смит и др. [52] на основе анализа изображений, полученных для желатиновых фантомов с графитовыми добавками, показали, что отношение сигнала к шуму близко к теоретическому значению, равному 2. Эти авторы исследовали также свойства автокорреляционной функции сигналов, формирующих акустические изображения, и нашли, что в поперечном направлении вид этой функции и ее зависимость от величины пространственного смещения хорошо согласуются с данными теоретических расчетов. В осевом направлении ширина автокорреляционной функции удовлетворительно коррелировала с длительностью импульса. Однако зависимость этой фукции от частоты и характерных размеров рассеивателей не исследовалась. Многое еще предстоит сделать с целью установления взаимосвязи между текстурой акустических изображений, параметрами преобразователей и структурой ткани.
Рис. 6.8. я — Зависимость коэффициента корреляции R двух демодулированных А-эхограмм от их смещения относительно друг друга в осевом и поперечном направлениях (кривые получены на фантоме ткани). Частота 1,5 МГц, ширина пучка 3,5 мм; б—временная зависимость коэффициента корреляции R двух А-эхограмм, разделенных интервалом времени 100 мс, представленная в сравнении с электрокардиограммой. По вертикальной оси отложена величина (1—R), пропорциональная смещению ткани между двумя сканированиями. Треугольниками отмечена R -волна на электрокардиограмме.
На рис. 6.8, а показаны зависимости коэффициента корреляции двух А-эхограмм от их пространственного смещения относительно друг друга. Видно, что эти зависимости имеют вид монотонно спадающих функций, на которые, как было установлено, влияют направление смещения, параметры излучаемого импульса и форма пучка, но не оказывает влияние структура ткани. Если сама ткань совершает какие-либо движения, то на основе анализа корреляции между двумя А-эхограммами, полученными при неподвижном преобразователе в различные моменты времени, можно оценить характер этого движения за соответствующий интервал времени. При этом рис. 6.8, а можно использовать в качестве калибровочной диаграммы. Подобный метод применялся для наблюдения динамики движения биологических тканей in vivo [18]. В качестве примера на рис. 6.8, б представлена временная зависимость коэффициента корреляции R между двумя А-эхограммами, полученными с интервалом времени 0,1 с. Видно, что в этой зависимости отражено движение, вызванное периодической сердечной деятельностью. Характер движения можно связать с пульсациями артериального давления, если предположить, что именно флуктуации артериального давления являются причиной такого движения.
В данном разделе было показано, каким образом свойства акустических изображений, полученных методом В-сканирования, можно описать на основе применения различных моделей ткани и теории рассеяния, учитывающей зависимость параметров рассеяния от времени. В следующем разделе рассматривается другой подход, позволяющий найти взаимосвязь между параметрами обратного рассеяния и свойствами биологической ткани. В основе этого подхода лежит представление среды в виде набора плоских слоев.
6.6.1. ПРОФИЛИ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ И АКУСТИЧЕСКОГО ИМПЕДАНСА
В гл. 1 для случая нормального падения плоской волны на плоскую границу раздела двух сред коэффициент отражения был определен в виде (см. (1.178))
![]()
где Zi и Zi — акустические импедансы сред, расположенных по обе стороны от границы, причем ![]() . Если импеданс является непрерывной функцией только одной пространственной координаты, то его можно представить в виде суммы малых приращений. При этом зависимость коэффициента отражения от координаты принимает вид [56]
. Если импеданс является непрерывной функцией только одной пространственной координаты, то его можно представить в виде суммы малых приращений. При этом зависимость коэффициента отражения от координаты принимает вид [56]
Если считать исходную волну плоской, pi(t-х/с), и пренебречь многократным рассеянием, то давление Ps(t) в волне, рассеянной в обратном направлении, можно представить следующим образом:
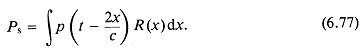
Данный метод получил название «импедиография» [29]. Более детальный анализ, учитывающий многократное рассеяние, дает
![]()
Преимущество метода импедиографии заключается в том, что он позволяет выразить взаимосвязь между А-эхограммой и акустическими параметрами среды через интеграл свертки. Этот метод особенно удобен, если исследуемый объект имеет слоистую структуру, как, например, глаз. Опубликован ряд работ, посвященных применению импедиографии к биологическим объектам in vivo [29]. Много усилий было сконцентрировано на поисках методов решения уравнения (6.77) с целью определения коэффицента R(x) [26].
6.6.2. ВЗАИМОСВЯЗЬ С РАССЕЯНИЕМ
Метод импедиографии позволяет установить взаимосвязь между параметрами А-эхограммы и параметрами ткани, причем эта взаимосвязь описывается выражением (6.76), аналогичным уравнению (6.60) из разд. 6.5, в котором фигурировала импульсная характеристика ткани. При малых флуктуациях плотности ![]() и сжимаемости (3 коэффициент отражения можно представить в виде
и сжимаемости (3 коэффициент отражения можно представить в виде
![]()
Таким образом, в данном случае импульсная характеристика ткани выражается через первую производную от параметров ткани, тогда как в трехмерном случае (6.60) она характеризуется производной второго порядка. Это расхождение является прямым следствием предположения об одномерности выбранной модели. Ниже представлено решение одномерного волнового уравнения, анализ которого позволяет выявить сходства и различия между двумя моделями.
Решение волнового уравнения для давления в обратно рассеянной волне можно представить в виде
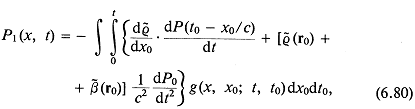
где g — функция Грина одномерной задачи, причем
![]()
Подстановка g в (6.80) и интегрирование по to дают
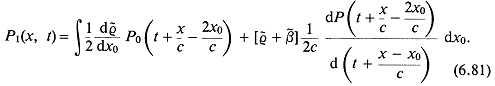
В результате интегрирования второго члена этого выражения по частям получаем
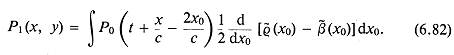
Можно видеть, что импульсная характеристика в данном случае идентична характеристике, полученной методом импедиографии в приближении малых изменений ![]() и
и ![]() . Другими словами, метод импедиографии хорошо работает в тех случаях, когда среду можно аппроксимировать одномерной моделью, а падающую волну можно считать плоской. В случае трехмерных структур анализ должен строиться на использовании импульсной характеристики ткани, определяемой уравнением (6.63). Лиман [35] предложил использовать понятие «эффективного импеданса», в котором учитывается профиль пучка. Хотя эта величина и не является однозначной функцией акустических характеристик ткани, она может быть весьма полезным параметром при характеризации ткани.
. Другими словами, метод импедиографии хорошо работает в тех случаях, когда среду можно аппроксимировать одномерной моделью, а падающую волну можно считать плоской. В случае трехмерных структур анализ должен строиться на использовании импульсной характеристики ткани, определяемой уравнением (6.63). Лиман [35] предложил использовать понятие «эффективного импеданса», в котором учитывается профиль пучка. Хотя эта величина и не является однозначной функцией акустических характеристик ткани, она может быть весьма полезным параметром при характеризации ткани.
Важное преимущество импедиографии по сравнению с подходом, основанным на теории рассеяния (см. разд. 6.5), состоит в том, что она позволяет учесть многократное рассеяние на основе применения выражения (6.75). Импедиографию можно рассматривать как полезное связующее звено между строгой теорией рассеяния, развитой в разд. 6.5, и простейшей теорией отражения.
При анализе рассеяния основная проблема заключается в том, чтобы с помощью какой-либо подходящей теории однозначно связать информацию, получаемую при экспериментальном исследовании рассеяния, с акустическими параметрами среды. Хотя в настоящее время разработан целый ряд простых теоретических моделей, позволяющих получить аналитические выражения для сечения рассеяния, они не дают исчерпывающего описания процесса рассеяния. На основе этих моделей удается сделать определенные качественные оценки характеристик рассеянного поля, однако очень трудно получить количественные данные, что в первую очередь связано с отсутствием сведений о многих параметрах. В результате трудно доказать корректность той или иной гипотетической модели, основываясь на имеющихся экспериментальных данных.
Определенные перспективы в плане более глубокого понимания процессов рассеяния звука в биологических тканях открываются в двух направлениях дальнейших исследований. Первое из них связано с развитием акустической микроскопии (гл. 9), которая в принципе позволяет проводить измерения скорости звука и акустического импеданса на образцах ткани in vitro в масштабе, значительно меньшем длин волн, характерных для диагностических применений ультразвука. На этой основе можно было бы получить реалистические модели характеристик ткани на микроскопическом уровне, исходя из результатов измерения соответствующих параметров рассеяния. Так, например, основываясь на результатах проведенных измерений, можно показать, что наличие в ткани определенной компоненты, такой как жир, коррелирует с усредненной величиной полного сечения обратного рассеяния. Акустическая микроскопия позволяет получить пространственное распределение такой рассеивающей компоненты и детально проанализировать ее роль в полном процессе рассеяния.
Второй путь, который мог бы привести к углублению нашего понимания рассеяния в тканях, заключается в реконструкции акустических параметров ткани (гл. 9). Цель методов реконструкции — получить пространственные распределения затухания, скорости звука и коэффициента обратного рассеяния, применяя ультразвуковое зондирование исследуемой области по ряду различных направлений и используя методику реконструкции, аналогичную рентгеновской компьютерной томографии. Помимо возможности получения количественных данных, подобные методы реконструкции характеризуются более высоким пространственным разрешением по сравнению со стандартным методом В-сканирования. Существует большое разнообразие методов реконструкции — от методов, в которых используется лучевое приближение и алгоритм итерационной реконструкции для разделения рассеяния и затухания [19], до методов синтезированной апертуры, позволяющих реконструировать величину сечения рассеяния по результатам измерения фазы сигнала в плоскости апертуры. В последнем случае может быть применена операция реконструкции, аналогичная операции свертки и обратной проекции в компьютерной томографии [45], или же численный метод решения волнового уравнения с использованием последовательных приближений. Подобный численный метод называется методом экстраполяции волнового поля, и первоначально он был разработан для сейсмологии [11, 48]. Для всех перечисленных методов характерным является тот факт, что реконструкция сечения рассеяния осуществляется независимо от затухания звука и конкретной схемы измерения. Поэтому есть надежда, что использование этих методов будет способствовать развитию наших представлений о тех структурах, которые ответственны за рассеяние. Следует также отметить, что все эти методы работают в приближении изотропного рассеяния, и успех или неудача их использования как раз и позволят установить, насколько справедливо допущение об изотропности рассеяния в случае биологических тканей. Кроме того, использование результатов теории рассеяния и проведение измерений углового распределения рассеяния также может помочь при выявлении принципиальных ограничений соответствующих методов и установлении тех изменений, которые необходимы для повышения их действенности.
Более глубокое понимание механизмов рассеяния в биологических тканях позволило бы определить принципиальные ограничения различных методов ультразвуковой диагностики, включая эхографический метод В-сканирования и количественные методы характе-ризации тканей (гл. 10). Так, например, по мере повышения разрешающей способности аппаратуры для В-сканирования все больший вклад в формирование изображения будут давать процессы рассеяния. Однако неизвестно, насколько при этом возрастет полезная информация в сравнении с генерацией спекл-шума. Необходимо найти оптимальное соотношение между спекл-шумом изображения и разрешающей способностью, и такая оптимизация может стать возможной только при наличии более полной информации о соответствующих параметрах рассеяния. Можно надеяться, что по мере углубления наших представлений о процессах рассеяния в биологических тканях нам удастся максимально повысить диагностическую информативность акустических изображений. В этом состоит основная причина необходимости проведения дальнейших исследований в этой области.
1. Abbott, J. G. & Thurstone, F. L. (1979). Acoustic speckle: theory and experimental analysis. Ultrasonic Imaging, 1, 303—324.
2. Ahuja, A. S. (1972). Effect of particle viscosity on propagation of sound in suspensions and emulsions. J. Acoust. Soc. Am. 51, 182—191.
3. Ahuja, A. S. & Hendee, W. R. (1977). Effects of red cell shape and orientation on propagation of sound in blood. Medical Fhysics, 4, 516—520.
4. Bamber, J. C. (1979a). Theoretical modelling of the acoustic scattering structure of human liver. Acoustics Letters, 3, 114—119.
5. Bamber, J. C. (1979b). Ultrasonic characterization of structure and pathology in human soft 'issue. PhD. Thesis. University of London.
6. Bamber, J. C, Hill, C. R., King, J. A., & Dunn, F. (1979). Ultrasonic propagation through fixed and unfixed tissues. Ultrasound in Med. & Biol., 5, 159—165.
7. Bamber, J. C. & Dickinson, R. J. (1980). Ultrasonic B-scanning: A computer simulation. Phys. Med. Biol., 25, 463—479.
8. Bamber, J. C. & Hill, C. R., (1981). Acoustic properties of normal and cancerous human liver. I. Dependence on pathological condition. Ultrasound in Med. & Biol., 7, 121—134.
9. Bamber, J. C, Hill, C. R., & King, J. A. (1981). Acoustic properties of normal and cancerous human liver. II. Dependence on tissue structure. Ultrasound in Med. & Biol., 7, 134—144.
10. Beecham, D. (1966). Ultrasonic scatter in metals. Its properties and its application to gain size determination. Ultrasonics, 4, 67—76. H. Berkhout, A. J., Ridder, J., & van der Wal, L. F. (1982). Acoustic imaging by wave field extrapolation. I. Theoretical considerations, Acoustical Imaging, Vol. 10. P. Alais & A. Metherell eds, pp. 513—540 (New York, Plenum).
12. Burckhardt, С. В. (1978). Speckle in ultrasound B-mode scans. IEEE Trans. Sonics & Ultrasonics, SU-26, 1—6.
13. Busse, L. J., Miller, J. G., Yuhas, D. E., Mimbs, J. W., Weiss, A. M., & Sobel, В. E. (1977). Phase cancellation effects: A source of attenuation artefact eliminated by a CdS accusto-electric receiver. Ultrasound in Medicine. Vol. 3B. D. White ed. pp. 1519—1535 (New York, Plenum).
14. Chernow, L. A. (1960). Wave propagation in a random medium. (Tr. R. A. Silverman) (New York, McGraw-Hill).
15. Chivers, R. C. (1977). The scattering of ultrasound by human tissues —some theoretical models. Ultrasound in Med. & Biol., 3, 1—13.
16. Chivers, R. C. (1978). Phase and amplitude fluctuations in the propagation of acoustic waves in lossless inhomogeneous continua with velocity, density and bulk modulus variations. Ultrasound in Med. & Biol., 4, 353—361.
17. Dickinson, R. J. (1982). A computer model for speckle in ultrasound images: theory and application, pp. 115—130 in Acoustical Imaging, Vol. 10. P. Alais & A. F. Metherell eds. (New York, Plenum).
18. Dickinson, R. J. & Hill, C. R. (1982). An ultrasonic technique for measuring soft tissue dynamics. Ultrasound in Med. & Biol., 8, 263—271.
19. Duck, F. A. & Hill, C. P. (1979). Acoustic attenuation reconstruction from back-scattered ultrasound. Computer aided tomography and ultrasonics in medicine. Ravieri et al. eds. pp. 137—149 (Amsterdam, North Holland).
20. Foldy, L. L. (1945). The multiple scattering of waves. 1. General theory of isotropic scattering by randomly distributed scatterers. Phys. Rev., 67, 107—119.,
21. Freese, M. & Lyons, E. A. (1977). Ultrasonic backscatter from human liver tissue: its dependence on frequency and protein/lipid composition. J. Clin. Ultrasound, 5, 307—312.
22. Gay, P. (1971). The crystalline state. (Edinburgh, Oliver & Boyd).
23. Goodman, J. W. (1976). Some fundamental properties of speckle. J. Opt. Soc. Am., 66, 1145—1150.
24. Gore, J. C. & Leeman, S. (1977). Ultrasonic backscattering from human tissue: A realistic model. Phys. Med. Biol., 22, 317—326.
25. Gramiak, R., Hunter, L. P., Lee, P. P. K., Gerner, R. M., Schenk, E., & Waag, R. C. (1976). Diffraction characterisation of tissue using ultrasound. Proc. Ultrasonics Symp. IEEE Cat. No. 76, CH1120-SSU, 60—63.
26. Herment, A., Perronneau, P., & Vayse, M. (1979). A new method of obtaining an acoustic impedance profile for characterization of tissue structures. Ultrasound in Med. & Biol., 5, 321—332.
27. Hill, C. R., Chivers, R. C, Huggins, R. W., & Nicholas, D. (1978). Scattering of Ultrasound by Human Tissue. Ultrasound: its applications in medicine and biology. F. J. Fry ed. (Amsterdam, Elsevier).
28. Ishimaru, A. (1978). Wave propagation and scatterring in random media. (New York, Academic).
29. Jones, J. P. (1977). Ultrasonic impediography and applications to tissue characterization. Chapter 6 Recent advances in ultrasound in biomedicine. Vol. 1. D. N. White ed.
30. Jones, J. P. & Kovac, (1980). A computerized data analysis system for ultrasonic tissue characterization. Acoustical imaging, Vol. 9. K. Y. Wang ed. (New York, Plenum).
31. Joynt, C. F. & Sommer, F. G. (1980). A stochastic approach to in vivo ultrasonic characterization of human liver tissue in normal and diffusely pathologic states. Abstract in 5th Int. Symposium on Ultrasonic Imaging and Tissue Chartacterization (Gaithersburg, NBS).
32. Julesz, В., Gilbert, E. N.. Shepp, L. A., & Frisch, H. L. (1973). Inability of humans to discriminate between visual textures that agree in second-order statistics — revisited. Perception, 2, 391—405.
33. Kerker, M. (1969). The scattering of light. (New York, Academic).
34. Koch, I. (1982). Ultrasonic backscattering from non-uniform scatterers.
Ultrasonic Imaging 4, 140—162.
35. Leeman, S. (1979). The impediography equations, Acoustical imaging, Vol. 8. D. F. Metherell ed. (New York, Plenum).
36. Lizzi, F. L. & Coleman, D. J. (1977). Ultrasonic spectrum analysis in ophthalmology, Chapter 5. Recent advances in ultrasound in biomedicine. D. N. White ed. (Forest Grove, Research Studies).
37. Morse, P. M. & Feshbach, H. (1953). Method of theoretical prysics. (New York,
38. Morse, P. M. & Ingard, K. N. (1968). Theoretical acoustics (New York, McGraw-Hill).
39. Nassiri, D. K., Nicholas, D., & Hill, C. R. (1979). Scattering and attenuation in anisotropic human tissue. Proc. 3rd European Cong. Ultrasound in Medicine, p. 381.
40. Nassiri, D. K. (1984). PhD. Thesis, University of London.
41. Nassiri, D. K., & Hill, C. R. (1985a). The differential and total bulk acoustic scattering cross sections of some human and animal tissues. (In press, J. Acoust, Soc. Am.).
42. Nassiri, D. K., & Hill, C. R. (1985b). The use of acoustic scattering measurements to estimate structural parameters of human and animal tissues. (In press, J. acoust. Soc. Am.).
43. Nicholas, D. (1979). Ultrasonic diffraction analysis in the investigation of liver disease. Brit. J. Radiol., 52, 949—961.
44. Nicholas, D. (1982). Evaluation of backscattering coefficients for excised human tissues: Results, interpretation and associated measurements. Ultrasound in Med. & Biol., 8, 17—28.
45. Norton, S. J. & Linzer, M. (1979). Ultrasonic reflectivity tomograpry: Reconstruction with circular transducer arrays. Ultrasonic Imaging, 1, 154—184.
46. Pauly, H. & Schwan, H. P. (1971). Mechanism of absorption of ultrasound in liver tissue. J. acoust. Soc. Am., 50, 692—699.
47. Pohlhammer, J. & O'Brien, W. P. (1981). Dependence of the ultrasonic scatter coefficient on collagen concentration in mammalian tissues. /. Acoust. Soc. Am., 69, 283—285.
48. Riddler, J., Berkhout, A. J., & van der Wal, L. F. (1982). Acoustic imaging by wave field extrapolation. II, Practical asspects. Acoustical imaging, Vol. 10. P. Alais & A. Metherell, eds. pp. 541—565 (New York, Plenum).
49. Shung, К. K., Sigelmann, R. A., & Reid, J. M. (1976). The scattering of ultrasound by blood. IEEE Trans. Biomed. Eng., 23, 460.
50. Shung, К. K., Sigelmann, R. A., & Reid, J. M. (1977). Angular dependence of scattering of ultrasound from blood. IEEE Trans. Biomed. Eng., 24, 325—331.
51. Sigelmann, R. A. & Reid, J. M. (1973). Analysis and measurement of ultra sound backscattering from an ensemble of scatter excited by sinewave bursts J. acoust. Soc. Am., 53, 1351—1355
52. Smith, S. W., Sandrik, J. M., Wagner, R. K, & Von Ramm (1982). Measurements and analysis of speckle in ultrasound B-scans. Acoustical imaging, Vol. 10, P. Alais & A. F. Metherell eds. pp. 195—212 (New York, Plenum).
53. Stephanishen, P. R. (1970). Transient radiation from pistons in an infinite planar baffle. J., acoust. Soc. Am., 49, 1629—1638.
54. Uscinski, B. J. (1977). The elements of wave propagation in random media. (New York: McGraw-Hill).
55. Waag, R. C, Gramiak, R., Gerner, R. M., & Schenk, E. A. (1976). Tissue macrostructure from ultrasound scattering. Proc. Con/, on Computerised Tomography in Radiolody, 175—186 (St. Louis, Am. Coll. of Radiology).
56. Wright, H. (1973). Impulse response function corresponding to reflection from a region of continuous impedance change. J. Acoust. Soc. Am., 53, 1356—1359.
МЕТОДЫ ВИЗУАЛИЗАЦИИ И ИССЛЕДОВАНИЯ
ВИЗУАЛИЗАЦИЯ В МЕДИЦИНЕ
К. Хидл
Идея создания изображений стара как мир, но мысль о том, что можно получать изображения внутренних структур живого человеческого тела, стала реальностью с открытием рентгеновских лучей в 1895 г. За последующие 50 лет это открытие не слишком далеко ушло от эмпирического уровня, и лишь начиная приблизительно с 1950 г. с появлением других методов, таких как радиоизотопная и ультразвуковая визуализация, термография, рентгеновская и ЯМР компьютерная томография, в этом направлении были достигнуты некоторые успехи и появились признаки формирования научного подхода. Несомненно, этому помогло одновременное развитие общих принципов визуализации в технике связи — развитие, нашедшее широкий отклик в промышленных и военных приложениях процессов записи, передачи и отображения графической информации.
При всем при этом предмет медицинской визуализации все еще остается неопределенным: прошли конференции и опубликованы прочитанные на них доклады по этому вопросу [7, 10], но приверженцы различных методов испытывают трудности в поиске связи своих методов с теми концепциями, что применяются в других дисциплинах [13]. Нет до сих пор и полноценных учебников по данному предмету. Цель этой главы — свести воедино те принципы, что лежат в основе общих процессов визуализации организма человека, в том числе принципы, пригодные для количественного представления изображения, а также физические ограничения и характеристики процесса визуализации. Многие из этих положений применимы не только к медицине, и их перечисление здесь полезно в качестве введения в детальный анализ различных методов ультразвуковой визуализации, изложенных в следующих главах.
Последующее изложение кратко и недостаточно подробно, однако по отдельным аспектам этого вопроса существует большое число работ. Интересное (особенно для физиков) введение в методы анализа изображений и особенности зрения человека дано в первой части книги [12], а более подробные и всесторонние исследования зрительного восприятия выполнены в работах [4, 6]. Работы [1, 11], ориентированные на инженеров, рассматривают, в частности, такой важный вопрос, как отношение сигнал/шум и его влияние на визуализацию. Труды конференции, специально посвященной вопросам формирования медицинских ультразвуковых изображений и восприятию [8], также отчасти связаны с тематикой этой и последующих глав.
7.2. КОЛИЧЕСТВЕННЫЕ ОПИСАНИЯ ПРИ ПОЛУЧЕНИИ И ВОСПРИЯТИИ ИЗОБРАЖЕНИЯ
Все изображения — это отражения некоторых аспектов реального мира в особом формате. В процессе визуализации некоторая количественная мера какой-либо характеристики реального мира (например, коэффициент отражения света, коэффициент поглощения рентгеновских лучей, коэффициент обратного рассеяния ультразвука или некая сложная функция нескольких таких величин) отображается на другую количественную меру (например, яркость изображения). Для конкретного процесса визуализации важно знать законы, определяющие количественную сторону такого отображения: преобразование полутоновой шкалы. Не менее важна мера статистики процесса — его зашумленность. Представляют интерес также пространственные свойства процесса, так как точка объекта на практике всегда отображается в пространственно распределенную область с соответствующей потерей разрешения и в общем случае с некоторым пространственным искажением. При медицинской визуализации исследователь имеет дело с живой, подвижной анатомией человека, а зрение специально приспособлено к восприятию движения. Поэтому было бы важно уметь количественно оценивать динамику процессов визуализации, особенно ультразвуковой, которая хорошо себя зарекомендовала при регистрации изображений движения тела и тканей.
7.2.1. ИЗМЕРЕНИЕ АМПЛИТУДЫ ОТОБРАЖАЕМОГО СИГНАЛА
Практическая мера амплитуды отображаемого сигнала в отдельном элементе изображения — плотность светового потока, приведенная к единице площади изображения. Эта мера называется энергетической яркостью элемента и определяется как отклик «стандартного наблюдателя» на свет, испущенный абсолютно черным телом при определенной температуре. Она физически эквивалентна эмпирически понимаемой «яркости», зависящей от наблюдателя [12]. Яркость измеряется в канделах на квадратный метр, т. е. в кд/м2 (нитах) или миллиламбертах (1 мЛ = 3,183 кд/м2). Некоторые типичные значения яркости изображений и окружающей среды приведены в табл. 7.1.
Таблица 7.1. Типичные уровни яркости изображений
Обстановка Яркость (кд/м2)
Белая бумага в солнечном свете 3•104
Наивысшая яркость экрана ЭЛТ1) 10
Комфортабельное освещение для чтения 30
Темная область экрана ЭЛТ1) 0,1
Белая бумага в лунном свете 0,03
1) Для любой электронно-лучевой трубки (ЭЛТ) отношение максимальной яркости к минимальной редко превышает 100:1 (обычно меньше).
7.2.2. МЕРЫ ПРОСТРАНСТВЕННЫХ ХАРАКТЕРИСТИК СИСТЕМ ВИЗУАЛИЗАЦИИ
Классический и, очевидно, самый прямой подход к выражению пространственных свойств систем визуализации таков. Преобразование стимула (в пространстве объекта) в сигнал (в соответствующем пространстве изображения) состоит в определении пространственного распределения сигнала изображения, который возникает от точечного тест-объекта. Такое распределение называется функцией рассеяния точки (ФРТ), а связанная с ним функция, соответствующая бесконечно тонкому линейному тест-объекту, — функцией рассеяния линии (ФРЛ).
При работе даже с простейшими системами визуализации такие формулировки оказываются неудовлетворительными, в том числе потому, что процедура вычисления комбинированного влияния на весь процесс визуализации множества ФРТ, каждая из которых вносит вклад на своей стадии процесса, математически заключается в вычислении ряда сверток. Таким образом, с точки зрения математики и вычислений проще и интуитивно понятнее работать в частотной области. Одномерное преобразование Фурье от ФРЛ называют оптической передаточной функцией (ОПФ). В общем случае это комплексная величина, модуль которой называется модуляционной передаточной функцией (МПФ). Для системы визуализации или любой ее части, таким образом, МПФ представляет собой отношение амплитуд множества пространственных гармонических составляющих, соответствующих изображению и оригиналу объекта, в зависимости от пространственных частот этих составляющих. При этом МПФ для многозвенной системы — произведение МПФ всех отдельных каскадов.
Такой подход к анализу систем визуализации, подробно изложенный Пирсоном [12], оказался весьма плодотворным. Важно заметить, однако, что его применимость в строгом смысле ограничена несколькими важными условиями, которые не встречаются в ряде медицинских систем визуализации, в том числе и ультразвуковых. К таким ограничениям относятся, например, требования линейности и пространственно-временной инвариантности (т. е. МПФ не должна изменяться ни во времени, ни на отображаемой поверхности), а также неотрицательности процессов. С последним требованием, означающим, что функция изображения не должна принимать отрицательных значений, можно столкнуться в системах визуализации с некогерентным излучением, например в рентгеновских или 7-радиоизотбпных [9], но не в когерентных системах, к которым относится большинство ультразвуковых систем.
Таким образом, хотя анализ пространственных характеристик ультразвуковых систем визуализации в частотной области может что-то объяснить и существуют общепризнанные методы преодоления некоторых из перечисленных ограничений, все же необходимы тщательные поиски более точных подходов.
7.3. ХАРАКТЕРИСТИКИ ЗРИТЕЛЬНОГО ВОСПРИЯТИЯ ЧЕЛОВЕКА
Общим для всех типов визуализации является то, что на некотором этапе изображение воспринимается глазами и мозгом оператора. Свойства зрительной системы человека, таким образом, являются центральным вопросом для визуализации, и хотя анатомию глаза (по крайней мере в простейшей форме) знают многие, некоторые существенные факты из области физиологии зрения могут быть малоизвестны тем, кто занимается разработкой и применением медицинских систем визуализации.
Чувствительность и разрешающая способность зрения тесно связаны со структурой сетчатки, чувствительными элементами которой являются колбочки и несколько более чувствительные палочки. Центральная область сетчатки, ямка (желтое пятно), занимающая в фокальной плоскости хрусталика дугу 1° — 2°, заполнена почти целиком плотно упакованными колбочками, а периферийные области — и колбочками, и палочками. Внутри ямки расстояние между колбочками довольно мало (~ 10 мкм), что позволяет достичь пространственного разрешения (измеренного по решетке) до 60 линий/градус. Чувствительность на более низких пространственных частотах при двух значениях яркости экрана (см. табл. 7.1) показано на рис. 7.1. Важно отметить подъем чувствительности примерно на 1 и 3 линиях/градус и существенное падение на низких частотах. Практически это означает, что существует предел восприятия мелкой детали (при ее наличии в образе), так что очень плавные границы (например, диффузно инфильтрированный край опухоли) можно легко потерять, если не принять специальных мер по обработке сигнала.
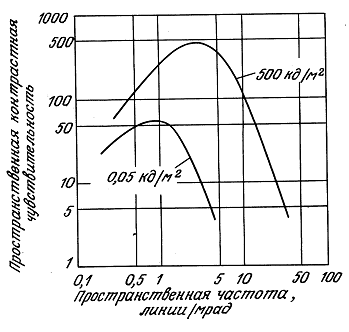
Рис. 7.1. Типичная контрастная чувствительность глаза, снятая с помощью теста с синусоидальным растром [12].
Лучше всего воспринимаются пространственные частоты в диапазоне 1—5 линий/градус. Последняя цифра может быть «хорошей» или «плохой» в зависимости от того, чему соответствует исследуемая деталь при данных структуре и увеличении изображения — реальной анатомии или артефакту (например, из-за рисунка растра или даже из-за когерентного спекл-шума; см. ниже).
Другая важная характеристика зрения, связанная с разрешением, — способность к восприятию контраста. Более полное обсуждение этого вопроса в связи с зашумленностью изображения приводится в следующем разделе, но здесь можно отметить, что восприятие контраста сильно зависит от резкости его границы. Резкие границы раздела, например, в градационном клине различаются достаточно хорошо, тогда как значительно отличающиеся по яркости области могут быть не опознаны, если они разделены плавным переходом.
Полный динамический диапазон человеческого глаза — около 80 дБ. В практике визуализации, однако, не весь он доступен. Практически верхняя граница (соответствующая максимальной яркости экрана ЭЛТ) — около 1000 кд/м2 (см. табл. 7.1), а при яркости ниже 0,003 кд/м2 ямка не работает и чувствительность можно повысить за счет пространственного разрешения объединением чувствительных элементов сетчатки.
7.3.1. ОСТРОТА ЗРЕНИЯ И ВОСПРИЯТИЕ ЯРКОСТНОГО КОНТРАСТА
Вышеупомянутое значение достижимого оптического пространственного разрешения — 60 линий/градус — представляет собой предел, диктуемый анатомией области ямки сетчатки, и имеет место лишь при больших уровнях освещенности и низком уровне шума. Анатомический предел остроты зрения не достигается по двум причинам: из-за процесса зрительного усреднения, который становится необходимым при недостаточном освещении, и из-за ограничений, налагаемых шумами изображения. Оба этих фактора будут здесь рассмотрены в аспекте, особенно важном в нескольких областях медицинской визуализации - в аспекте разрешения по контрасту, т. е. способности различать соседние области по яркости изображения.
Определение и измерение разрешения по контрасту, даже при отсутствии значительного шума, было темой большого исследования, и для подробной оценки различных факторов следует обратиться к специальной литературе, например к гл. 5 работы [6]. Были выполнены эксперименты, в которых наблюдателям предъявляли большой экран, подсвеченный в двух смежных областях с различными, но постоянными по уровню яркостями, и проверяли способность испытуемых обнаружить разность уровней. Порог разрешения по контрасту AL/L определяется разностью яркостей AL, которая еще воспринимается в 50% наблюдений при заданной яркости L. Величина AL/L, называемая отношением Вебера, значительно меняется в зависимости от светового потока, падающего на сетчатку, как это показано на рис. 7.2.
Рис. 7.2 показывает, что глаз человека способен в идеальных условиях (яркое освещение и резкая граница между двумя полубесконечными областями объекта) различить уровни яркости, отличающиеся лишь на 1%. На практике ситуация обычно резко ухудшается в результате действия четырех факторов: использования освещен ности ниже оптимальной, отсутствия резких границ (значение этого фактора уже обсуждалось в связи с рис. 7.1), недостаточности площади тест-объекта (мишени) для различения и, наконец, наличия шумов и помех. Рассмотрим теперь эти последние два фактора.
.
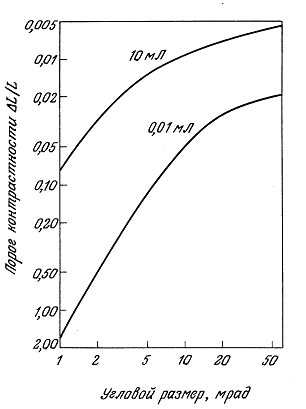
Рис. 7.2. Зависимость порогового контраста ![]() L/L (отношения Вебера) от размера наблюдаемого круглого диска при двух уровнях фоновой яркости, нулевом уровне шума и времени наблюдения 6 с [2]. Действие аддитивного шума и/или сокращения времени наблюдения сводится в основном к росту пороговой контрастности по сравнению с указанными здесь уровнями
L/L (отношения Вебера) от размера наблюдаемого круглого диска при двух уровнях фоновой яркости, нулевом уровне шума и времени наблюдения 6 с [2]. Действие аддитивного шума и/или сокращения времени наблюдения сводится в основном к росту пороговой контрастности по сравнению с указанными здесь уровнями
В большой серии экспериментов Блекуэлл [2] показал, как способность наблюдателя обнаруживать присутствие круглой мишени на контрастном фоне зависит от величины контраста, уровня освещенности и углового размера тест-объекта (мишени). Для этого контраст определяется как С = (BS – В0)/Во, где Во — яркость фона, Bs — яркость мишени, Bs > Во (при BS<B0 С = (В0 - Bs/B0). Эта зависимость показана на рис. 7.2. Из представленных данных, в частности, видно, что для заданного уровня яркости существует обратная зависимость между линейным размером мишени и степенью контраста, необходимой для ее различения. Хотя иногда утверждается, что эта зависимость обратно пропорциональна, это приближение, очевидно, справедливо лишь в ограниченном интервале размеров мишени.
Влияние шума изображения на его восприятие подверглось серьезному исследованию, в том числе в связи с задачами электрооптической визуализации и проблемой фотографического «зерна». В данном случае удобно расширить понятие шума, включив в него сосредоточенную «помеху» (термин, который имеет более общее значение, чем просто нежелательный сигнал). Важное различие между шумом и помехой состоит в том, что шум имеет некогерентную природу, а помеха может быть частично когерентна с сигналом.
Кроме интегрального уровня шума очень важно его эффективное распределение по пространственным частотам. Количественно эту зависимость можно исследовать, измеряя степень модуляции, необходимую для визуального различения периодической картины полос (растра) в зависимости от пространственной частоты. В работах по распознаванию образов эту функцию иногда называют функцией необходимой модуляции (ФНМ).
Применение этого понятия показано на рис. 7.3, где построены ФНМ и МПФ для одной и той же системы визуализации. Экспериментально обнаружено, что площадь между этими двумя кривыми при построении их в линейном масштабе (площадь модуляционной передаточной функции, или ПМПФ) — хорошая оценка качества визуализации для предсказания способности оператора распознавать отдельные образы. Отсюда следует, что шум будет оказывать наибольшее воздействие на понижение способности распознавания, если это происходит при пространственных частотах, при которых МПФ имеет большие значения. Важность этого результата для различных типов ультразвуковой визуализации будет видна в последующих главах.
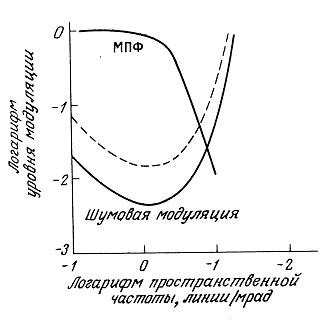
Рис. 7.3. Связь модуляционной передаточной функции (МПФ) с шумовой модуляцией в процессе визуализации. Штриховая кривая показывает действие роста уровня шума. Площадь между двумя характеристиками называют площадью модуляционной передаточной функции (ПМПФ) [1].
Эксперименты, в которых в оптическое изображение искусственно вносились шумы типа зернистости, показывают, что наблюдатель, если ему предоставлен выбор, стремится скорректировать увеличение так, чтобы спектр пространственных частот воспринимаемого изображения оставался постоянным. Отсюда ясно, что при создании практических систем должны быть обеспечены оптимальный набор увеличений и возможность их выбора оператором.
В связи с медицинской визуализацией, где изображение получают, чтобы помочь в конкретной задаче обнаружения или распознавания патологии, важна и характеризация данных самого оператора-диагноста. В работе с оптическим образом формально можно выделить три этапа восприятия объекта: обнаружение (факт наличия объекта), распознавание (различение класса, к которому относится объект,например: дом, человек и т. д.) и идентификация (описание объекта на втором уровне детализации, например: гостиница, полисмен и т. д.). Кроме того, эти этапы восприятия эмпирически оказались связаны с обнаружимостью структуры полос заданной пространственной частоты (при одинаковых условиях визуализации и степени модуляции). Так, установлено, что обнаружение, распознавание и идентификация происходят при угловой ширине мишени ![]() , 4/v к 6,5/v, где v — период наивысшей обнаружимой пространственной частоты (в линиях на единицу угла). Это несколько упрощенное утверждение можно, однако, оценить, если заметить, что на практике на действенность такого восприятия будут влиять несколько других факторов, в том числе время, отводимое на выполнение задания, и априорное ожидание обнаружить особый объект на некотором участке «сцены». Было бы интересно исследовать возможное распространение этого подхода к действиям оператора в некоторых конкретных приложениях медицинской визуализации.
, 4/v к 6,5/v, где v — период наивысшей обнаружимой пространственной частоты (в линиях на единицу угла). Это несколько упрощенное утверждение можно, однако, оценить, если заметить, что на практике на действенность такого восприятия будут влиять несколько других факторов, в том числе время, отводимое на выполнение задания, и априорное ожидание обнаружить особый объект на некотором участке «сцены». Было бы интересно исследовать возможное распространение этого подхода к действиям оператора в некоторых конкретных приложениях медицинской визуализации.
Необходимо иметь в виду, что выше обсуждалось в основном зрительное восприятие образа человеком. В некоторых случаях для улучшения чувственного восприятия (например, при ограниченном разрешении по контрасту) может применяться индикация путем замещения или добавления к человеческому зрению искусственных средств. Хорошо известный пример таких возможностей — выделение желаемого сигнала из некогерентного шума путем усреднения. Тем не менее могут существовать пределы возможностей в этом направлении: отношение сигнал/шум в медицинских изображениях в общем случае имеет предел из-за необходимости избегать излишнего облучения пациента. Так что здесь может стать главной проблема когерентных помех, для которых методы искусственного улучшения качества изображения еще только исследуются.
7.3.2. ФАКТОР ВРЕМЕНИ В ЗРИТЕЛЬНОМ ВОСПРИЯТИИ
В зрительном восприятии человека имеются по крайней мере два различных, зависящих от времени фактора, которые необходимо учитывать при обсуждении визуализации: реакция на световой стимул сам по себе и временной ход процесса распознавания образов и признаков на более высоких уровнях работы мозга. О последнем факторе кратко говорилось выше, и здесь обсуждение ограничится непосредственно процессом зрения.
Зрение человека устроено так, что движение воспринимается специфически. По аналогии с пространственным откликом количественно это можно измерить и выразить как частотно-временную характеристику «чувствительности к мельканию» [12]. Если яркость небольшого источника с равномерно распределенной светимостью гармонически флуктуирует вокруг среднего значения L, результирующий стимул имеет вид
![]() ,
,
где ![]() — амплитуда флуктуаций, f — их частота. Если величину
— амплитуда флуктуаций, f — их частота. Если величину ![]() , определяющую пороговую чувствительность к мельканию, определить экспериментально как функцию частоты f, то отношение
, определяющую пороговую чувствительность к мельканию, определить экспериментально как функцию частоты f, то отношение ![]() составит чувствительность к мельканию, или временной контраст.
составит чувствительность к мельканию, или временной контраст.
Типичный отклик человеческого глаза при обычных условиях наблюдения за изображением на дисплее показан на рис. 7.4. Видно, что при низких уровнях яркости глаз ведет себя как интегрирующая цепь с постоянной времени - 0,2 с. При большей яркости система сильно подавляет относительно статичные детали изображения и наиболее чувствительна на частоте - 8 Гц. Критерий отсутствия мелькания, очевидно, означает, что процедура наблюдения соответствует участку отрицательного наклона кривой отклика, а относительные флуктуации яркости должны быть ниже некоторого значения, определяемого частотой мелькания. Это ограничение при средних уровнях яркости менее строгое, чем при больших.

Рис. 7.4. Типичная чувствительность глаза к мельканию для двух уровней освещенности сетчатки [12].
7.4. МЕСТО УЛЬТРАЗВУКА В МЕДИЦИНСКОЙ ВИЗУАЛИЗАЦИИ
В следующих трех главах мы несколько подробнее опишем отдельные методы медицинской визуализации, основанные на применении ультразвука. Поэтому здесь в связи с тем, что уже было сказано о предмете визуализации, уместно рассмотреть некоторые причины того, почему для этой цели следует применять именно ультразвук.
Одно из преимуществ ультразвуковых методов визуализации, обычно выдвигаемое на передний план, — их относительная безопасность. Некоторые доказательства для утверждений такого рода приведены в гл. 14, а здесь мы сформулируем этот тезис в следующем виде: «при уровнях экспозиции, соответствующих данной степени риска для пациента, ультразвук способен обеспечить значительно большее отношение сигнал/шум в изображении, чем системы медицинской визуализации, основанные на применении ионизирующего излучения». На практике именно отношение сигнала к шуму и его влияние на такие параметры, как разрешение по контрасту, в конечном счете определяют минимальную дозу облучения, достижимую в рентгеновской и радиоизотопной визуализации. В случае ультразвука, однако, ограничение обычно определяется факторами, не связанными с радиационной безопасностью, хотя отношение сигнал/шум и остается первостепенно важным.
Как было показано в предыдущих главах, ультразвук взаимодействует с тканями органов человека по-разному и зачастую весьма специфично: значения таких параметров, как коэффициенты обратного рассеяния и затухания, у разных, но анатомически близких тканей могут существенно отличаться. Сам этот факт служит основой способности ультразвука обеспечить достаточное число градаций контрастности и для некоторых диагностических задач может дать важное преимущество, например, перед рентгеновской визуализацией, где коэффициент поглощения может быть малочувствителен к гистопатологическим изменениям. В последнее время возрос интерес к методам так называемой ультразвуковой характери-зации биологических тканей (гл. 10). Развитие этой области направлено на создание количественных и объективных процедур, которые в терминах визуализации можно рассматривать как поиск параметров изображения, обеспечивающих более четкое различение в конкретных ситуациях и тем самым возможность еще большего улучшения контрастности.
Другим важным свойством, влияющим на возможности разрешения по контрасту, является возможность отделять сигналы от интерферирующих с мишенью областей (например, от вышележащих тканей). Эта возможность, очевидно, присуща основным методам ультразвуковой визуализации, тогда как в рентгеновском и радиоизотопном методах это часто достигается за счет стоимости и сложности (например, путем компьютерной реконструкции образа).
Основные требования к любому излучению, применяемому для визуализации, — чтобы его распространение было геометрически предсказуемо, а затухание в исследуемой среде — не очень сильным. Эти требования должны выполняться на частотах, для которых направленность, определяемая дифракцией, соответствует необходимому пространственному разрешению. Другими словами, длины волн должны быть малы по сравнению с изучаемым объектом. Одно из замечательных явлений природы — то, что всем этим требованиям удовлетворяет распространение ультразвука в мягких тканях организма. Отклонение и деформация пучков происходят, но не настолько, чтобы качество изображения значительно ухудшалось. Затухание существенно (иначе не было бы взаимодействий, используемых для визуализации), но допускает проникновение сигнала в мягкие ткани на глубину порядка 300 длин волн (в мегагерцевом диапазоне частот), что обеспечивает получение изображений с достаточным отношением «сигнал/шум» при работе как в режиме обратного рассеяния, так и в трансмиссионном режиме. На практике, как будет подробно показано ниже, дифракция ограничивает разрешение величиной порядка нескольких миллиметров.
Еще одна особенность ультразвука как средства для визуализации в медицинских применениях (помимо удобства технической реализации и уменьшения риска лучевого поражения для пациента, о чем уже упоминалось) — это возможность получать высококачественные быстро сменяющиеся изображения с частотой кадров выше пороговой частоты, за которой наблюдатель уже не воспринимает мелькания. В этом отношении ультразвук несомненно превосходит все другие средства визуализации.
7.5. СИСТЕМАТИКА ИНТЕРПРЕТАЦИИ ИЗОБРАЖЕНИЙ
Вся работа, связанная с получением изображений — точно так же, как любая работа по представлению медицинской информации в той или иной форме, — имеет смысл лишь тогда, когда она нацелена на оптимизацию качества решений, на улучшение диагностики. Так, конкретное ультразвуковое обследование (например, В-скани рование брюшной полости при беременности или измерение бипа-риетального диаметра головки плода) выполняется, чтобы ответить на конкретные вопросы в отношении пациента. Вопросы могут быть частными (например, каков размер головки плода) или более общими (например, есть ли у плода какая-либо анатомическая патология), но в любом случае неявно предполагается, что правильный ответ существует и что в ходе обследования именно его и надеются получить.
На практике лишь очень немногие процедуры дают гарантированно правильный ответ на интересующий вопрос. Отчасти это связано с тем, что изначально «зашумлены» сами процедуры. И в этой главе мы уже обсуждали физические проявления шума в ультразвуковых системах визуализации. Необходимо также иметь в виду, что там, где частью системы интерпретации является человек, он может представлять собой основной источник «шума», который, впрочем, уменьшается по мере обучения и роста квалификации.
Очевидно, что процесс принятия решения, связанный с интерпретацией медицинских изображений и сопутствующих массивов данных, было бы полезно как-то систематизировать.
По типу решений, которые нужно принимать в ходе интерпретации изображения, весь процесс можно разделить на три этапа. Первый — обнаружение (ответ на вопрос: есть ли аномалия?), второй — локализация (где аномалия находится?), третий — классификация (что это за аномалия?). Лучше всего исследовано и лучше всего понято обнаружение, хотя, впрочем, и локализацию, и классификацию с известной пользой можно было бы рассматривать как модификации задачи обнаружения.
Очевидно, что качество диагностических решений, принимаемых в результате процедуры вызуализации (или какой-либо другой подобной процедуры), важно уметь оценивать. И некоторый формальный подход, в частности в связи с задачей обнаружения, для этого уже развит. В рамках такого подхода заранее предполагается, что есть правильный ответ («Да» или «Нет») на вопрос о наличии аномалии. Далее, с этим ответом (истинным решением) мы можем сравнить результат визуализации (фактическое решение). При анализе фактических решений их то или иное число N (или долю F) будем характеризовать индексами, которые соответствовали бы четырем возможным ситуациям в оценках. Статистику решений свяжем со следующей матрицей индексов:
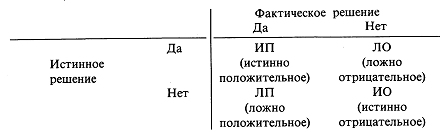
На основе указанного формального подхода можно количественно оценить качество диагностической процедуры. Обычно используют такие величины:
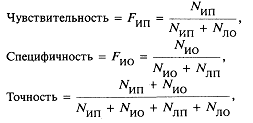
Здесь важно иметь в виду некоторые соображения относительно объективности такого анализа. На первое место необходимо поставить вероятность преднамеренного или случайного смещения оценки. Всегда существует некоторое ожидаемое значение отношения нормы и патологии, и если оно выбрано неверно, это приведет к смещению результата. Однако гораздо важнее то, что в конкретном случае на решение диагноста может сильно влиять знание о его последствиях. Рассмотрим, например, воображаемую ситуацию, когда диагност использует ультразвуковой сканер сначала для осмотра группы, по-видимому, здоровых женщин на предмет обнаружения признаков рака молочной железы, а затем — для обследования какой-то одной женщины с подозрением на поражение молочной железы с целью принятия решения о необходимости хирургического вмешательства. В первом случае статистическое ожидание аномалии будет очень малым, но последствия большой доли ложно положительных решений будут относительно умеренными, поскольку подавляющее число пациентов подвергнется дальнейшему осмотру. Таким образом, здесь будет вполне обоснованным смещение к достижению большей чувствительности ценой уменьшения специфичности. Во втором случае ожидание аномалии значительно больше, но диагност должен иметь возможность сообщить хирургу степень достоверности своей оценки.
Другая особенность состоит в том, что (если перефразировать замечание Оскара Уайльда) истина редко бывает полной и никогда не бывает простой. Неявно заложенное в приведенную выше матрицу предположение о том, что всегда можно узнать «истинную» оценку аномалии, нереально. Лучшее, на что можно надеяться в «определительной диагностике», — гистопатологической отчет после операции, биопсии или вскрытия. Но это не всегда возможно, и в любом случае не избавляет от значительной неопределенности.
Ясно, что простые меры, такие как чувствительность, специфичность или даже точность, не могут служить объективным показателем качества решений, принимаемых при конкретной процедуре визуализации. Гораздо лучшим индикатором может служить так называемая рабочая характеристика диагноста (РХД). Она получается (рис. 7.5) как график зависимости доли истинно положительных решений от доли ложно положительных решений. Отдельные точки на этой кривой получают путем повторения теста несколько раз с различной степенью смещения оценки (или порога принятия решения) по отношению к ожиданию положительного результата. Различные кривые на рисунке показывают разное качество принятия решения: диагональ — результат полностью неинформативного теста, а линии, наиболее близко подходящие к осям FЛП = 0 и FИП = 1 соответствуют наилучшему результату [5].
Анализ с помощью РХД можно использовать, чтобы сравнить способность обнаружения различных аномалий и сравнить действенность (в смысле облегчения принятия решений) как систем визуализации, так и операторов, или и тех и других.
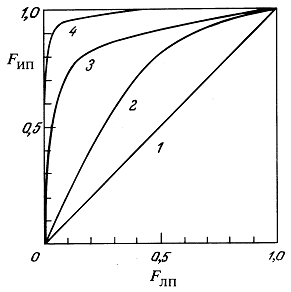
Рис. 7.5. Примеры «рабочей характеристики диагноста». Чем выше и левее лежит РХД, тем вероятнее обнаружение сигнала.
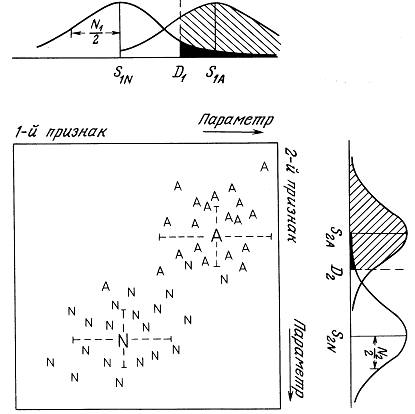
Рис. 7.6. Иллюстрация разделения признаков, ограниченного «шумом». Сигналы для двух различных признаков характеризуются расстоянием между ними (например, S1a – S1n) и шириной их «шумового спектра» (например, N1). Устанавливаемый порог принятия решения (например, D1 определяет вероятность принятия истинного (заштрихованная область) и ложного (зачерненная область) решения. Показаны также соответствующие двумерные распределения в пространстве признаков.
Однако это может быть очень длительная процедура, и полезно отметить, что столь же хорошие результаты можно получить с помощью более быстрой процедуры классификации [3]. При этом наблюдатель должен был выразить степень своей уверенности в наличии аномалии, например, в категориях «0-20%», «20-40%» и т. д.
Иногда полезно рассмотреть процедуру принятия решения на модели, в которой разделение нормального и аномального сигналов ограничивается шумом (рис. 7.6). При этом «сигналами» могут быть любые из большого числа возможных количественных характеристик изображения (например, уровень серого, сглаженность границы поражения и т. д.), а шум порождается оператором, системой визуализации и/или изменениями самого объекта. В этой модели очень ярко видно, как выбор порога принятия решения в некотором месте шкалы амплитуд сигнала влияет на само решение. Эта модель также показывает, что решения, принятые оператором или машиной, часто основаны на нескольких отдельных параметрах, для каждого из которых имеется своя ограниченная шумом степень разделения сигналов. При этом решение будет принято (оператором или компьютером) в многомерном пространстве признаков (на рисунке представлено двумерное пространство).
1. Biberman, L. M. (ed.) (1973) Perception of displayed information, Plenum Press, New York.
2. Blackwell, H. R. (1946) Contrast thresholds of the human eye. J. opt. Soc. Amer. 36, 624—643.
3. Chesters, M. S. (1982) Perception and evaluation of images, in Scientific basis of medical imaging, pp. 237—280 (ed. P. N. T. Wells), Churchill, Edinburgh.
4. Cornsweet, T. N. (1970) Visual perception, Academic Press, New York. 5. Green, D. M. & Swets, J. A. (1966) Signal detection theory and psychophy-
sics. Wiley, New York.
6. Haber, R. N. & Hershenson M. (1973) The psychology of visual perception, Holt, Rinehart, and Winston, New York.
7. Hay, G. A. (ed.) (1977) Medical images: formation, perception and measurement. Wiley, New York.
8. Hill, C. R. & Kratochwil, A. (1981) Medical ultrasonic images: formation, display, recording and perception. Excerpta Medica, Amsterdam.
9. Metz. С. E. & Doi, K. (1979) Transfer function analysis of radiographic imaging systems, Phys. Med Biol. 24, 1079—1106.
10. Moores, В. M. (1981) Physical aspects of medical imaging. Wiley, Chichester.
11. Overington, I. (1976) Vision and acquisition. Pentech Press, London.
12. Pearson, D. E. (1975) Transmission and display of pictorial information. Pentech Press, London.
13. Wells, P. N. T. (1982) Scientific basis of medical imaging. Churchill, Edinburgh.
ЭХО-ИМПУЛЬСНЫЕ МЕТОДЫ ВИЗУАЛИЗАЦИИ И ИЗМЕРЕНИЙ
К. Хилл
Методы ультразвуковой эхо-импульсной визуализации уже нашли широкое и разнообразное применение в медицине, хотя заложенные в их основу научные принципы еще не до конца поняты. Быстро развивается и связанная с этими методами технология. Цель главы — оценить существующий уровень знания принципов эхо-импульсной визуализации; в основном для иллюстрации будут описаны также некоторые конкретные применения.
Существующие эхо-импульсные системы насчитывают много видов. Можно представить (довольно условно), что все они состоят из шести основных взаимосвязанных частей (рис. 8.1). Зондирование объекта (мишени) осуществляется через контактную среду (например, водяной буфер или тонкий слой геля).
Основным элементом любой системы визуализации является электроакустический преобразователь, который служит для излучения зондирующего акустического импульса в объект и для приема акустических эхо-сигналов, переизлучаемых мишенью. Преобразователь может представлять собой пластинку из пьезоэлектрического материала или (все чаще) одно- или двумерную решетку (матрицу) пьезоэлементов. Разделение функций приема и передачи между преобразователями обладает рядом преимуществ, в том числе связанных с отношением сигнал/шум, и применяется все чаще, особенно в многоэлементных решетках. Обсуждение работы преобразователей и их пространственно-временных характеристик приведено в гл. 2. Полезное введение в конструирование и свойства различных видов многоэлементных преобразователей дано Фогелем с соавт. [28].
Для большинства применений эхолокации необходимо знать точное расположение преобразователя и/или ориентацию оси пучка в пространстве. При этом в такой системе отсчета можно правильно определить положение обнаруженных целей. На практике сканирование (движение оси пучка через обследуемый объем) можно выполнить одним из трех способов: путем перемещения всего пре образователя с фиксированным направлением пучка вручную или с использованием механического привода, а также путем движения пучка относительно неподвижного преобразователя (решетки), что достигается с помощью электронного управления. Все три способа требуют наличия механического или электронного растра, чтобы ограничить движение пучка определенной областью и одновременно получить электрические сигналы, определяющие положение пучка.
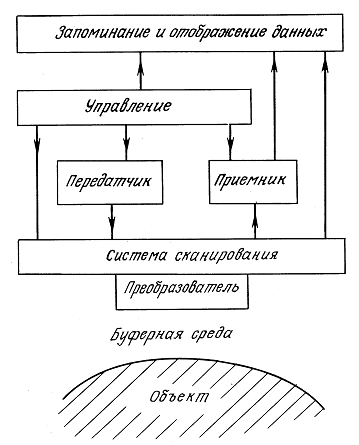
Рис. 8.1. Блок-схема, показывающая взаимосвязь между основными узлами эхо-импульсных диагностических систем.
Роль передающего тракта понятна: она состоит в ударном возбуждении преобразователя — обычно скачком напряжения с достаточно крутым фронтом, чтобы большая часть энергии попадала в полосу резонансных частот преобразователя. Один из факторов, определяющих отношение сигнал/шум, — амплитуда возбуждающего импульса напряжения, но она ограничена практическим требованием не допустить чрезмерных нелинейных эффектов при распространении акустических импульсов в среде, а также электрического пробоя или нелинейного режима в работе преобразователя и требованием ограничения уровня акустической энергии, излучаемой в тело пациента. На практике обычно используются электрические импульсы возбуждения с амплитудой порядка 100 В.
Приемник представляет собой своего рода систему сопряжения между преобразователем и дисплеем или системой записи, которые применяются для передачи наблюдателю информации, полученной с помощью ультразвука. В хороших системах эхо-сигналы на выходе преобразователя имеют большой динамический диапазон. Так, сигналы от сильно отражающей плоской поверхности (например, границы вода/стекло), если они не ослаблены, превышают уровень шума более чем на 80 дБ. Затухание эхо-сигналов указанной силы, принятых от мишени, будет приблизительно пропорциональным длине пути распространения в вышележащих тканях. Это затухание можно приближенно скорректировать с помощью временной автоматической регулировки усиления (ВАРУ). Но даже остающийся после ВАРУ динамический диапазон (обычно около 40 дБ) все еще слишком велик для большей части систем отображения и регистрации, поэтому необходимо его дальнейшее сжатие.
Процесс передачи к оператору множества изображений и другой информации, извлекаемой из амплитуды и фазы высокочастотного сигнала, часто может ограничивать предельно возможную полезность этой информации. Реальные средства отображения информации, а также восприятие наблюдателя, как правило, чувствительны только к амплитуде и для их функционирования требуется применять выпрямленную видеоверсию исходного сигнала, из которого удалена информация о фазе. (Некоторые частные характеристики систем отображения будут обсуждаться ниже.)
Устройством отображения, почти повсеместно применяемым для ультразвуковой эхо-импульсной визуализации, служит электронно-лучевая трубка (ЭЛТ). Поэтому состояние разработок и характеристики систем визуализации сильно зависят от характеристик ЭЛТ (полосы частот, размера светящейся точки на экране, динамического диапазона). В настоящее время общепринятыми являются два основных режима отображения — непосредственное отображение видеосигнала с выхода приемного тракта и отображение сигнала с промежуточного запоминающего устройства (преобразователя развертки или кадрового запоминающего устройства). Из-за практического удобства последний режим применяется все чаще, так как он позволяет хранить и анализировать изображения, не прибегая к непрерывной регистрации (фотографированию и т. п.), а также позволяет делать выбор процедуры обработки или анализа данных, соответствующих изображению или какой-то его части. Важным достоинством режима промежуточного запоминания является то, что он обеспечивает сопряжение параметров сканирования, обусловленных особенностями ультразвука и анатомического строения человека, и стандартных телевизионных устройств, что выгодно с точки зрения стоимости и доступности техники.
Из-за широкого распространения режима промежуточного запоминания, быстрого развития киноэхографии — метода эхографии в реальном времени, а также из-за удорожания серебросодержащих фотографических материалов диагностические оценки все чаще проводятся по изображению на экране ЭЛТ, а не по записи (твердой копии), полученной с помощью регистратора. Тем не менее обычно требуется иметь некоторое количество выбранных изображений в виде постоянной записи, и в этой связи важными оказываются известные свойства процессов фотографической регистрации [12, 22]. Во многих отношениях в качестве регистратора видеомагнитофон значительно лучше фотокамеры приспособлен к современным средствам отображения.
В любой ультразвуковой видеосистеме основная проблема — это управление различными процессами и их координация. Частично эту работу может выполнить оператор (например, при ручном сканировании), но многочисленные задачи синхронизации и вычисления координат изображения должна решать ЭВМ.
8.2. РЕЖИМЫ ПРЕДСТАВЛЕНИЯ ЭХО-ИМПУЛЬСНОЙ ИНФОРМАЦИИ
В эхо-импульсных методах А-сканирование — простейший и исторически первый режим отображения. В таком режиме амплитуда радио- или видеосигнала (т. е. сигнала выпрямленного и зачастую профильтрованного), полученного из принятой последовательности эхо-сигналов, отображается на ЭЛТ как вертикальное отклонение; горизонтальную (временную) развертку можно преобразовать в шкалу расстояний, если скорость звука известна. В условиях почти всеобщей доступности устройств для двумерной визуализации А-ре-жим, за исключением некоторых специальных областей применения, сейчас довольно редко используется самостоятельно. Там, где анатомия достаточно проста (или считается таковой) и не требуется двумерное изображение, А-режим продолжает применяться и важен (особенно в радиочастотной форме) при точных измерениях размеров, например, в офтальмологии.
Сохранение фазовой информации в радиочастотной эхограмме типа А имеет большую потенциальную ценность в некоторых существующих и предлагаемых методах характеризации тканей (гл. 10).
Развитием А-режима является режим отображения движущихся органов (тип ТМ, или М), разработанный в основном для исследования сокращений сердца на интервале времени, соответствующем нескольким кардиоциклам. При этом координаты по дальности А-эхограммы считываются по вертикальной оси, амплитуда видеосигнала модулирует яркость строки и все получаемые строки с течением времени медленно разворачиваются вдоль горизонтальной оси. Таким способом можно исследовать движения различных структур сердца в норме и патологии. Характерная М-эхокардио-грамма приведена на рис. 8.8. М-режим до некоторых пор очень широко использовался независимо от режима двумерной визуализации, однако благодаря развитию эхографии в реальном масштабе времени в настоящее время есть тенденция к объединению этих двух режимов. Соответствующее устройство должно иметь возможность работы в очень узком акустически прозрачном окне для доступа к сердцу и обеспечивать достаточно высокую частоту коммутации выборок в М-режиме (порядка 100 Гц), чтобы регистрировать быстрые движения клапанов сердца.
Принцип В-сканирования хорошо известен, так как он является основой почти всех современных практических средств ультразвуковой визуализации. Его можно рассматривать как тот же А-режим, но в котором последовательность импульсов видеосигнала используется для модуляции яркости в плоскости изображения вдоль линии, соответствующей положению оси ультразвукового пучка в сечении объекта в данный момент времени. Сканирование сечения объекта пучком позволяет построить изображение, модулированное по яркости. Следует, однако, иметь в виду, что, несмотря на большую практическую ценность, эта процедура в каком-то смысле произвольна и ее использование определяется удобством, а не какими-либо соображениями научного характера. Из материала, изложенного в других главах, видно, что в принципе могут существовать методы визуализации иных параметров, нежели распределение амплитуды эхо-сигнала. Эти методы труднее реализовать, но они более чувствительны к патологии и анатомическим изменениям в организме и отражают эти изменения точнее, чем карта распределения амплитуд эхо-сигнала, которая к тому же неизвестным образом искажена за счет затухания в тканях.
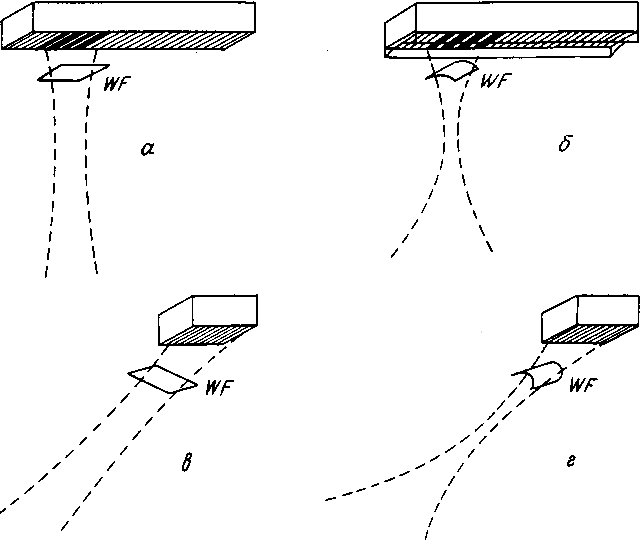
Рис. 8.2. Принципы ультразвукового сканирования, отклонения и фокусировки пучка с помощью многоэлементной решетки преобразователей. Показаны характерные положения волновых фронтов (WF).
Процесс сканирования — движение оси пучка в плоскости сканирования — может быть выполнен двумя основными способами: либо механическим перемещением преобразователя при неподвижной оси пучка, либо, при электронном управлении, перемещением оси пучка относительно преобразователя, неподвижного в пространстве. Устройства первого типа, включающие как ручные секторные сканеры, так и автоматические сканеры, приводимые в движение электромоторами, требуют применения механического сканирования, например с помощью движущегося кронштейна или ротора, что обеспечивает непрерывный контроль за пространственными координатами преобразователя. Устройства второго типа, в которых информацию о положении несут электронные управляющие сигналы, включают линейные и фазированные решетки, показанные на рис. 8.2. Как будет подробно описано далее, все приборы этого типа (а иногда и первого) могут вырабатывать последовательность изображений с частотой кадров, исключающей мелькание (больше 10 Гц; гл. 7).

Рис. 8.3. Ряд изображений мочевого пузыря, полученных в режиме С (с постоянной глубиной), при указанных постоянных значениях глубины, отсчитываемых от поверхности кожи.
Визуализация в В-режиме — основная тема этой главы; различные приложения метода рассмотрены в разд. 8.9, а некоторые примеры применения приведены на рис. 8.5—8.8.
Несколько иная процедура — сканирование с постоянной глубиной (С-режим). При этом сканируется плоскость объекта, параллельная плоскости перемещения зонда и нормальная к оси пучка, а фиксированное расстояние между плоскостями устанавливается путем стробирования эхо-сигнала по времени. Амплитуда строби-рованного сигнала модулирует яркость в плоскости изображения. Как станет ясно из дальнейшего обсуждения, перед Всканированием эта процедура обладает тем интересным преимуществом, что визуализацию можно осуществлять в фокальной области сильно сфокусированного пучка; кроме того, модуляционная передаточная функция (МПФ) при этом однородна и изотропна (не зависит от координат и направления). Эта процедура сравнительно редко используется (отчасти из-за низкой скорости сканирования), но этот недостаток можно значительно скомпенсировать применением линейной решетки преобразователей для обеспечения быстрого движения по одной из координат. В качестве иллюстрации на рис. 8.3 показаны несколько изображений, полученных при С-сканировании ([13]).
Выше были просто перечислены возможности импульсных эхо-локационных методов, применяемых в медицине, а сейчас мы рассмотрим физику процессов, участвующих в формальном описании процедуры визуализации, при которой двумерное множество данных f(x, у) в пространстве объекта порождает двумерный образ g(x, у) с помощью передаточной функции системы h(x, у):
![]()
где ![]() — свертка. В области пространственных частот существует соотношение
— свертка. В области пространственных частот существует соотношение
![]()
В следующих подразделах будет использоваться в общем виде понятие передаточной функции, с помощью которого будет рассмотрено формирование эхо-импульсного изображения. При этом, однако, необходимо иметь в виду замечания, сделанные в разд. 7.2 относительно справедливости анализа с помощью МПФ.
Биологические объекты обычно сложны по структуре и не поддаются строгому математическому анализу, поэтому весьма полезно будет рассмотреть случай более простых объектов. Как уже отмечалось, при анализе процесса формирования изображения в В-режиме импульсные отклики системы вдоль и поперек оси пучка необходимо рассматривать независимо (что не обязательно для С-режима).
В качестве модели ультразвукового пучка удобно рассматривать пучок, создаваемый идеальным круглым излучающим поршнем. Как указывалось в гл. 2, обычно это может служить хорошим первым приближением, но необходимо иметь в виду, что реальный пучок далек от этого идеала из-за случайных изменений амплитуды и фазы по его сечению, а также из-за того, что излучатель по форме нередко бывает некруглым. Поперечная структура поля идеального круглого излучателя уже была описана (см. разд. 1.6). Здесь же можно отметить, что в ультразвуке, как и в оптике, дифракционный предел разрешения выражается через угловой размер (в радианах) диска Эйри (центральной зоны дифракционной картины для круглой апертуры радиуса ![]() ):
):
![]()
Так, например, угол расходимости в дальней зоне излучателя, работающего на частоте 3 МГц в воде (![]() =0,5 мм) при радиусе плоского излучателя 10 мм составляет около 3,5°.
=0,5 мм) при радиусе плоского излучателя 10 мм составляет около 3,5°.
Отсюда определяется дифракционный предел поперечной разрешающей способности системы даже при наличии фокусировки пучка (акустическими линзами или за счет кривизны самого фокусирующего излучателя). В этом случае при фокусном расстоянии f теоретически достижимый предел разрешения, т. е. минимальный диаметр фокального пятна, равен
![]()
Для предыдущего примера фокусировка на 50 мм дает (определенный таким путем) предел разрешения около 3 мм.
Другая мера дифракционного предела разрешающей способности — ширина амплитудного распределения пучка в фокусе на уровне 0,5, которая, согласно теории дифракции Фраунгофера, составляет
![]()
Еще одна мера разрешения, применяемая при анализе в частотной области, — дифракционный предел для пространственных частот:
![]()
На практике ни одну из этих мер пространственного разрешения нельзя назвать наиболее удачной (см. разд. 8.8), но они тем не менее полезны, поскольку позволяют оценить границы применимости данного типа визуализации, правда с учетом, в частности, того, что из-за когерентности излучения эти показатели могут еще несколько ухудшиться (разд. 2.4).
При анализе и сравнении фокусирующих акустических систем полезным параметром оказывается степень фокусировки, определяемая (см. гл. 2, уравнение (2.4)) как отношение теоретически вычисленной продольной координаты дальней зоны к фокусному расстоянию (или радиусу кривизны фокусирующего преобразователя):
![]()
При использовании преобразователей с постоянным фокусным расстоянием в разных способах визуализации требуются различные оптимальные значения степени фокусировки. Режим сканирования типа С, в котором необходимо малое фокусное расстояние, лучше выполнять с сильно фокусирующим преобразователем (![]() = 10-15), а при контактном сканировании типа В, где ситуация противоположна, значение
= 10-15), а при контактном сканировании типа В, где ситуация противоположна, значение ![]() должно быть меньше 3, чтобы обеспечить хотя бы удовлетворительное разрешение на всех глубинах, представляющих интерес. Промежуточным случаем является В-сканирование через водяной буфер.
должно быть меньше 3, чтобы обеспечить хотя бы удовлетворительное разрешение на всех глубинах, представляющих интерес. Промежуточным случаем является В-сканирование через водяной буфер.
Продольное разрешение в эхо-импульных системах определяется прежде всего эффективной длительностью эхо-сигнала от точечной мишени, а она в свою очередь определяется эффективной длительностью излученного зондирующего импульса. На практике без потери чувствительности довольно просто достичь лучшего разрешения в продольном направлении, а не в поперечном. Например, для рассмотренного выше случая (довольно типичного для пучков, используемых при контактном сканировании брюшной полости) для получения продольного разрешения, лучшего, чем поперечное (3 мм), необходимо, чтобы длины излученного и принятых импульсов были меньше 6 мм, что соответствует 4 мкс, т. е. 12 периодам на частоте 3 МГц, тогда как обычно они составляют 2—3 периода.
Как будет видно далее, важно учитывать, что истинная функция рассеяния точки (ФРТ) при В-сканировании имеет форму радиочастотного сигнала и, следовательно, содержит отрицательные значения (что заведомо исключает ее из рассмотрения в обычной теории визуализации).
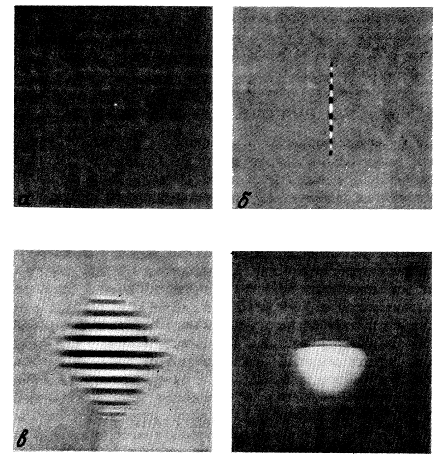
Рис. 8.4. Иллюстрация эволюции функции рассеяния точки при получении В изображения (размеры, приведенные ниже, выражены в пикселах, т. е. в количестве элементарных ячеек: полное изображение — 100х100 таких ячеек: а — точечный объект; б — распределение после свертки со звуковым импульсом (длина волны = 6, время нарастания импульса = 6, время спада = 8); в — распределение после свертки с профилем пучка (ширина на уровне 0,5 равна 30); г — распределение после детектирования и сглаживания (время отклика фильтра = 9) [4].
Примеры вычисленных ФРТ в случае В-сканирования до и после выпрямления и фильтрации представлены на рис. 8.4. Рассматривались различные методы обращения свертки для выделения истинного распределения по объекту из получаемого изображения, но, хотя подобное обращение свертки в продольном направлении осуществить относительно просто, реально требуется улучшить именно поперечное разрешение, а это как раз весьма сложно сделать. Одна из возможностей такого рода, предложенная Сомером [27], предусматривает использование методов параллельной обработки.
Многие важные объекты в медицинской ультразвуковой визуализации ведут себя как трехмерные распределения рассеивателей (см. гл. 6). Этот случай можно математически смоделировать либо неоднородным континуумом значений плотности и сжимаемости, либо эффективным распределением точечных рассеивателей. Такой подход оказывается очень информативным (см. разд. 6.3) и, в частности, может объяснить, почему в изображении типа В такого органа, как печень, анатомическая информация может сильно модулироваться артефактом когерентного излучения, приводя к появлению характерного спекл-шума.
Факторы, влияющие на пространственное разрешение протяженного объекта на контрастном фоне, обсуждались в гл. 7, откуда следует, что когерентный спекл-шум может служить источником шума изображения или помехи.
Многие биологические объекты, в частности границы раздела органов, имеют поперечную протяженность порядка многих длин волн и поэтому могут оказаться зеркальными отражателями. Так, например, в работе [8] было показано, что паразитное отражение от диафрагмальной перегородки привело к тому, что изображения структур печени оказались на месте легких. Лили, Куэнтин и ряд других исследователей провели наблюдения зеркальности таких отражений и показали, что поверхность может быть акустически шероховатой, что приводит к диффузному отражению пучка в некотором диапазоне углов вблизи направления зеркального отражения. Тем не менее в общем случае маловероятно, чтобы произвольная граница раздела своей нормалью была ориентирована достаточно близко к зондирующему пучку и, следовательно, чтобы зеркально отраженный сигнал возвращался к преобразователю. Для увеличения вероятности такого зеркального отражения была предложена методика сложного сканирования со многих направлений. Она была особенно полезной для наблюдения головки плода с помощью низкочувствительной техники.
8.4. СЛОЖНОЕ СКАНИРОВАНИЕ И НЕКОГЕРЕНТНОСТЬ ИЗОБРАЖЕНИЯ
С появлением оборудования, обладающего улучшенным пространственным разрешением и чувствительностью, а также с учетом смещения прикладных интересов (от простого получения границ органов к визуализации тканей) методика сложного сканирования, т. е. зондирования под различными углами с последующим синтезом сигналов изображений, стала применяться сравнительно редко. Отчасти это связано с заметным расплыванием изображения, которое может произойти из-за смещения органов, если время получения изображения велико.
Интересное (хотя до сих пор и не оцененное) свойство методики сложного сканирования состоит в том, что при этом подавляется когерентность процесса визуализации, о которой говорилось выше. Вероятно, именно этот фактор приводит к наблюдаемому различию изображений, полученных способами простого и сложного сканирования е сравнимых условиях (см. рис. 8.6). Использование решеток преобразователей позволило успешно реализовать этот принцип и снять проблему движения тканей. Бёркхардт [7] высказал мысль, что необходимым условием устранения когерентности двух зондирующих пучков является то, что точки пересечения их осей с преобразователем должны быть разнесены не менее чем на один диаметр его апертуры. Среди других возможных подходов к подавлению когерентности и, следовательно, спекл-шума, можно назвать умножение частоты [20] и использование регистрации, нечувствительной к фазе [23], хотя успех любой из этих процедур может быть достигнут ценой некоторой потери контрастности. Многообещающий подход к этой задаче предложил Бэмбер [3] — это создание двумерного адаптивного пространственного фильтра, способного узнавать (например, по изображению фантома) частотный спектр, соответствующий когерентному спекл-шуму в данной системе, что применяется затем для избирательного улучшения изображений реальных структур. На рис. 8.7 будет показано действие такой обработки.
8.5. ВЛИЯНИЕ СРЕДЫ РАСПРОСТРАНЕНИЯ
В предыдущих главах рассматривались различные аспекты распространения акустической волны; здесь необходимо лишь отметить, что свойства среды, в которой распространяется звук, и, в частности, свойства вышележащих тканей могут существенно влиять на передаточную функцию изображения в эхо-импульсной системе.
Основным фактором является затухание звука в тканях, и, как отмечалось выше, его можно приближенно скорректировать часто применяемой на практике системой ВАРУ (автоматическим увеличением усиления приемника с течением времени после каждого зондирующего акустического импульса). Такая приближенная компенсация в обычных эхо-импульсных системах не позволяет получать данные, которые можно было бы считать количественно обоснованными в метрологическом смысле (возможные подходы к такой метрологии обсуждаются в разд. 9.5). Акустическое затухание действует как дисперсионный фильтр, селективно ослабляющий высокочастотные составляющие спектра излучаемого импульса. В принципе этот эффект можно скомпенсировать путем управляемой фильтрации, но она крайне редко, если вообще применяется. Таким образом, области изображения типа В, находящиеся на различных глубинах, формируются как бы различными рабочими частотами.
Возможно, более существенным фактором при распространении является неоднородность скорости звука (а значит, и показателя преломления) в тканях, которая может привести к искажению фазы волнового фронта и тем самым к отклонению и уширению пучка, а также к аномальным изменениям затухания [10]. Этот эффект может быть особенно важен для гетерогенных органов, таких как молочная железа, и может определять оптимальное значение фокусного расстояния преобразователя.
В предыдущих разделах обсуждались акустические аспекты передаточной функции эхо-импульсной системы визуализации. Теперь мы обратимся к электронным и оптическим узлам этих систем и кратко рассмотрим их вклад в передаточную функцию. Хотя такая классификация может быть достаточно произвольной, удобно рассматривать четыре аспекта обработки сигнала: влияние шума, частотную фильтрацию, коррекцию характеристик системы отображения, а также специальные процедуры, причем последний вопрос будет рассматриваться в гл. 10 в связи с задачами характеризации тканей.
Как отмечалось в предыдущей главе, шум накладывает основное ограничение на функционирование любой системы визуализации. В частности, его происхождение и уровень определяют максимально возможное усиление сигнала, еще не приводящее к его ограничению. При заданном методе визуализации и определенном уровне шума частотно-зависимое затухание в тканях практически определяет ограничение частоты сверху и, следовательно, предел пространственного разрешения.
В хорошей системе отношение сигнал/шум должно определяться прежде всего цепями, в которых уровень сигнала минимален (для эхо-импульсной системы — преобразователем), и должно примерно соответствовать теоретическому среднеквадратичному уровню шума, определяемому шириной полосы частот ![]() (Гц) и импедансом Z(Ом), а именно при нормальной температуре среды напряжение шумов равно
(Гц) и импедансом Z(Ом), а именно при нормальной температуре среды напряжение шумов равно
![]()
На практике для многих систем это равенство не выполняется, а характеристики систем ограничиваются максимально возможным уровнем подавления источников шумов и интерференционных явлений.
Все составные части реальных систем имеют ограниченную частотную характеристику, и необходимо учитывать этот факт при разработке сложных систем.
Эхо-импульсная система должна быть спроектирована так, чтобы гарантировать прохождение ультразвука через ткани до определенной глубины, заданной назначением прибора (например, для диагностики внутренних органов, структур глаза и т. д), а также обеспечить, чтобы рассеянный сигнал превышал некоторый уровень шума. На практике это почти всегда достигается опытным путем, но, как можно видеть из других глав этой книги, при научном подходе можно обобщить основные выводы для получения оптимальных критериев конструирования.
Ткань является фильтром низкой частоты, поэтому эффективная частота, соответствующая наибольшей глубине проникновения, может оказаться значительно ниже центральной частоты спектра излучаемого импульса. Полоса пропускания системы должна перекрывать диапазон, содержащий обе эти частоты. Для снижения уровня шума необходимо отсекать частоты значительно выше и ниже указанных, сохраняя однако полосу частот, необходимую для передачи быстро меняющейся во времени информации. Отсечка нижних частот может быть особенно важна, потому что в эту область могут попадать нежелательные резонансные частоты преобразователя.
Если прибор рассчитан на работу с двумя или более зондами, имеющими различные центральные частоты, желательно иметь возможность переключать полосы частот.
8.6.3. ОБРАБОТКА ИНФОРМАЦИИ ДЛЯ ОТОБРАЖЕНИЯ
Мы уже отмечали, что непосредственное представление эхо-импульсной информации для качественного отображения непригодно. В частности, хотя есть техническая возможность высокочастотную информацию отобразить на ЭЛТ в виде модуляции яркости относительно среднего уровня серого, глаз человека не сможет эффективно воспринять ее в сложном изображении. Кроме того, ЭЛТ и другие средства отображения обладают специфическими ограничениями по динамическому диапазону и по полосе пространственных частот, что необходимо иметь в виду при разработке систем отображения.
Процесс сглаживания или детектирования, высокочастотного сигнала и получения так называемого видеосигнала — стандартная операция в видеотехнике. Так как ширина полосы пропускания модулятора яркости многих дисплеев и запоминающих устройств может быть значительно уже, чем у сигнала на несущей частоте, на этом этапе часто бывает необходимо применять ФНЧ. В свою очередь это может привести к некоторому искажению передаточной функции (см. рис. 8.4). Однако, так как фильтрация влияет только на продольное (аксиальное) разрешение, она будет иметь практическое значение лишь для высокочастотных ультразвуковых систем (например, используемых в офтальмологии).
Уже отмечались как необходимость применения ВАРУ для коррекции амплитуды импульсов, искаженной затуханием в тканях, так и очевидная субъективность этой процедуры в стандартных системах. Даже при использовании ВАРУ динамический диапазон сигналов, принимаемых от различных рассеивающих структур в тканях, все еще значителен. Так, при проектировании систем часто используют оценку в 40 дБ как требование к диапазону, необходимому для высокого качества диагностики (это диапазон между сильными сигналами, еще не вызывающими ограничения в приемном тракте, и слабыми сигналами, выделяемыми на уровне шума). Так как эта величина почти вдвое превышает динамический диапазон, свойственный самым высококачественным устройствам отображения, необходимо некоторое сжатие сигналов, что представляет собой особый вид нелинейного усиления. В общем случае нелинейное усиление требуется еще и по совсем другой причине — для адекватного согласования уровней сигнала в изображении с характеристиками зрения человека. В этом смысле сам усилитель — просто одно из звеньев последовательности нелинейных элементов в цепи, включающей в себя также устройство отображения, глаз, а иногда и устройство для фотографирования или другого подобного процесса. Для правильного выбора параметров сжатия в усилителе необходимо помнить обо всем этом, хотя обычно этот выбор основан на субъективной оценке качества изображения. В некоторых приборах имеется возможность выбора различных законов сжатия сигнала, выполняемого в высокочастотном тракте до или после запоминания изображения.
Иногда используются методы дополнительной обработки, позволяющие с помощью электроники дифференцировать форму волны эхо-сигналов и путем комбинирования в некоторой пропорции исходного и дифференцированного сигналов несколько подчеркнуть контуры изображения в продольном направлении. Другой фактор, который может влиять на окончательный вид изображения, — правила, используемые для запоминания изображений при сложном сканировании. Так, если одна точка изображения соответствует более чем одному значению полученных данных, в цифровой памяти можно реализовать режим обработки этих данных (например, усреднение, выделение максимального значения) и окончательный вид изображения будет зависеть от выбранного алгоритма обработки [24].
Вышеописанные подходы к обработке изображений носят до некоторой степени эмпирический характер; значительного улучшения диагностической эффективности изображений можно достичь с помощью методов, основанных на физической интерпретации причин появления истинных и ложных сигналов в изображении ([3], см. рис. 8.6).
8.7. ОГРАНИЧЕНИЕ СКОРОСТИ СКАНИРОВАНИЯ И ЧАСТОТЫ КАДРОВ
Обычная процедура получения эхо-импульсных изображений заключается в последовательной записи ряда отдельных эхограмм (строк изображения). Время получения одной эхограммы от объекта, расположенного на глубине, не превышающей d, есть
![]()
где с — скорость звука в веществе объекта. Минимальное время получения изображения, состоящего из n строк, составляет
![]()
Таким образом, время получения изображения из 100 строк (сравнительно бедная выборка), перекрывающих глубину до 10 см в мягкой ткани (с ![]() 1500 м/с) ti = 2 • 100 • 0,1/1500
1500 м/с) ti = 2 • 100 • 0,1/1500 ![]() 13 мс. На практике это значение несколько больше, но тем не менее вполне реально получить приемлемое качество изображения с частотой кадров 10-20Гц, на которой чувствительность человеческого глаза к изменению яркости низка (см. гл. 7, рис. 7.4). Это обеспечивает основу для создания немелькающих систем визуализации, работающих в реальном времени.
13 мс. На практике это значение несколько больше, но тем не менее вполне реально получить приемлемое качество изображения с частотой кадров 10-20Гц, на которой чувствительность человеческого глаза к изменению яркости низка (см. гл. 7, рис. 7.4). Это обеспечивает основу для создания немелькающих систем визуализации, работающих в реальном времени.
Системы реального времени с механическим сканированием могут быть нескольких видов. Можно перемещать преобразователь вдоль линии, перпендикулярной оси пучка, можно вращать или периодически качать его вокруг точки на оси пучка (обычно вблизи ее пересечения с поверхностью преобразователя). Можно также регулярно отклонять пучок неподвижного преобразователя с помощью движущихся зеркал или призм. Поскольку конструкция преобразователя не требует отклонения с помощью электроники, качество получаемых изображений в такой системе может быть очень высоким. Однако здесь существует ограничение, важное, в частности, в кардиологии: отдельные строки в растре нельзя выделять с частотой, превышающей кадровую.
Имеющиеся системы электронного сканирования бывают двух типов (хотя иногда встречаются и смешанные): с поперечным сканированием (линейные решетки) и с угловым сканированием (фазируемые решетки) (рис. 8.2). Оба типа представляют собой одномерные матрицы полосковых преобразователей. Фокусировка (если она применяется) осуществляется в направлении, перпендикулярном плоскости сканирования, с помощью неподвижных цилиндрических линз или за счет кривизны повеохности преобразователя.
В матрице с поперечным сканированием группы соседних элементов (следующих друг за другом от п до n + m, где обычно m=3, ...7) используются для передачи и приема в направлении, примерно перпендикулярном к поверхности преобразователя. В такой матрице ширина отдельного элементарного преобразователя обычно сравнима с длиной волны, что дает значительную направленность. В простейшем виде сканирование такой решетки заключается в выборе значений п из следующего ряда: 1, 2, 3, (N - m), где N — число элементов матрицы, a (N - m) — число линий сканирования. С другой стороны, сканирование в чрезстрочном режиме (n = 1, 3, 5, ... и т. д. ... n - 2, 4, 6, ...) можно использовать для приближения характеристик изображения как к временным, так и к пространственным частотным характеристикам глаза. Фокусировка на плоскость сканирования (неподвижный фокус) в режиме излучения (и/или ступенчатая фокусировка в режиме приема) часто обеспечивается путем введения необходимых задержек между элементами, входящими в активную группу преобразователя (т. е. путем формирования волновых фронтов).
При угловом сканировании с помощью фазированной решетки направление пучка меняется в широких пределах (обычно ±40°) относительно нормали к поверхности зонда. При этом требуется обеспечить слабую направленность элементов преобразователя (например, 6 дБ под углом 40°), и их ширина должна быть на порядок меньше длины волны. В таком приборе фокусировка в плоскости сканирования (как и ранее) и отклонение пучка осуществляются путем объединения элементов, выбранных из всей апертуры преобразователя, с требуемыми взаимными задержками, причем зачастую с разделением функций излучения и приема между разными группами элементов [26].
Практическое значение методов, работающих в реальном времени, т. е. в режиме так называемой киноультрасонографии, многообразно. И прежде всего — эти методы, очевидно, способны отображать картину смещения тканей и органов, давать богатую информацию о физиологических и патологических изменениях в организме. Однако во многих приложениях не менее важна возможность трехмерного отображения путем регулярного качания плоскости сканирования в протяженной области анатомических структур таким образом, что у оператора создается полное впечатление трехмерности изображения, например, плода, системы кровеносных сосудов или области патологии.
При использовании многоэлементных зондов для визуализации в реальном времени возможны несколько интересных вариантов. Один из них — построение двумерной матрицы преобразователей, которые можно применять для качания и фокусировки пучка в трехмерной области пространства (а не в плоскости, как в случае одномерной матрицы). Другое предложение — окружить исследуемую область (например, молочную железу) множеством расположенных на полусфере преобразователей, каждый из которых может принимать эхо-сигналы, вызванные излучением остальных преобразователей. Можно ожидать, что такое расположение обеспечит большой объем точных данных, к тому же с кадровой частотой вплоть до нескольких килогерц.
8.8. ИСПЫТАНИЯ И ОЦЕНКА ХАРАКТЕРИСТИК СИСТЕМ
Во многих ситуациях желательно иметь возможность объективно проверить, измерять диагностические характеристики эхо-импульсных систем, например, при проектировании и производстве новой аппаратуры, при оценке закупаемого оборудования, при текущем обслуживании и анализе результатов исследований. Разработка подобных методик измерения — поле деятельности многих исследователей и групп, в том числе Международной электротехнической комиссии [1, 6, 15].
Объем книги позволяет лишь кратко рассмотреть эту проблему, и для более полного ее обсуждения необходимо обратиться к указанным источникам. Эту тему лучше всего рассматривать, разделяя качества системы на несколько взаимосвязанных показателей, таких как эффективная мощность зондирующего излучения, способность обнаружения данного эхо-сигнала на фоне шума и интерференционных помех, пространственное разрешение и геометрическое подобие изображения.
Степень проникновения ультразвука с заданной начальной интенсивностью в какую-либо поглощающую среду зависит прежде всего от частоты. Поскольку все поглотители, в том числе и ткани, действуют как НЧ-фильтр, прохождение короткого (широкополосного) импульса зависит от формы его спектра и в особенности от распределения энергии по спектру для всей системы (в том числе и при усилении высокочастотного сигнала).
Способность к обнаружению эхо-сигнала — особый критерий, зависящий прежде всего от амплитуды передаваемого импульса, от эффективности электроакустического преобразования, от уровня шума и интерференционных помех, на фоне которых необходимо обнаружить заданный сигнал, например от стандартного отражателя в виде стального шарика диаметром 5 мм [19]. Так как по техническим причинам и из соображений безопасности пациента амплитуда излучаемого импульса на практике ограничена достаточно узкими рамками, этот параметр действительно является мерой отношения сигнал/шум для системы.
Выше обсуждались меры пространственного разрешения для точечных и распределенных мишеней и проблемы, связанные с их точным определением. Измерения в продольном и поперечном по отношению к пучку направлениях требуют несколько отличных методик, но в обоих случаях их результаты лучше всего выражать через ширину огибающей импульса или профиль пучка, соответствующий эхо-сигналу от точечного объекта, например от маленького стального шарика. При этом уровни боковых лепестков и «звона» преобразователя могут быть существенными, и желательно определять значения ФРТ, например, на уровнях -6 и -20 дБ.
Геометрическое подобие — важный, притом весьма простой показатель качества. Он отражает способность системы визуализации, во-первых, давать изображение без пространственных искажений, а, во-вторых, при наблюдении объекта из нескольких точек регистрировать разные изображения одинаково. Оба этих фактора чрезвычайно важны в случае систем, работающих в режиме сложного сканирования. Для других систем некоторые искажения с учетом естественной деформируемости органов человека допустимы, но уже любое требование измерения размеров будет накладывать свое ограничение на величину искажений.
В указанной выше литературе описаны и другие критерии качества, в том числе и характеризующие систему отображения: способ преобразования шкалы амплитуд принятых эхо-сигналов в отображаемые величины (яркость экрана, вертикальное отклонение для А-эхограмм и т. д.). Критерием или группой критериев, весьма далеких от строгого определения, являются способность систем различать распределенные объекты, отличающиеся друг от друга заданным образом. Здесь могут пригодиться понятие ПМПФ (разд. 7.3.1), а также использование соответствующих испытательных «фантомов», имитирующих биологические ткани [25].
8.9. ОБЛАСТИ ПРИМЕНЕНИЯ ЭХО-ИМПУЛЬСНЫХ МЕТОДОВ
Эхо-импульсные методы в настоящее время стали широко применяться во многих областях медицины, и появилось большое количество литературы — учебников [9, 29], справочников [5, 14], трудов конференций [2, 31], ежегодных обзоров и выпусков по последним достижениям в этой области [17, 18], обзорных статей [21], специальных журналов (Clinics in Diagnostic Ultrasound; Journal of Clinical Ultrasound; Journal of Ultrasound in Medicine; Ultrasound in Medicine and Biology) и статей в радиологических и других журналах. Приведенные здесь источники далеко не исчерпывают эту тему, но и их достаточно, чтобы читатель получил представление о предмете. В следующих разделах обсуждается сущность клинических задач, которые сейчас решаются в различных областях медицины с помощью эхо-импульсной техники, как стандартной, так и экспериментальной.
Акушерство — та область медицины, где эхо-импульсные ультразвуковые методы наиболее прочно укоренились как составная часть медицинской практики. Рассматриваемые здесь четыре основных задачи иллюстрируют ценность многих полезных свойств ультразвуковых методов.
Надежное определение положения плаценты — задача первостепенной важности в акушерской практике. С развитием техники, обеспечивающей высокое разрешение по контрасту, эта процедура стала уже рутинной. Приборы, работающие в реальном времени, эргономически более выгодны, так как позволяют определять положение плаценты быстрее, чем статические сканеры.
Второй вид процедур, ставших уже привычными, — оценка развития плода по измерению одного или более его размеров, таких как диаметр головки (обычно измеряемый бипариетально), окружность головки, площадь грудной клетки или живота (рис. 8.5). Так как даже очень малые изменения этих размеров могут иметь диагностическое значение, эти методы требуют высокой точности самой аппаратуры и методик ее применения.
Третий вид процедур, появившийся не так давно и не столь еще укоренившийся в практике, — раннее обнаружение аномалий плода. Это приложение требует особенно хорошего пространственного разрешения и разрешения по контрасту, предпочтительно в сочетании с режимом реального времени и быстрым сканированием.
Рис. 8.5. Участок изображения, иллюстрирующий измерения двух различных параметров, используемых для оценки роста плода: а — бипариетальный диаметр, принимаемый за размер головки плода (стрелки); буквой «с» обозначена cavum septum pellucidum; б —продольное сечение матки на 13-й неделе беременности, показывающее размер, принимаемый за длину плода (стрелки) (из работы [11], с согласия д-ра Р. Сандерса).
Хорошие методики и качественная аппаратура позволяют обнаруживать такие дефекты, как недоразвитие (гибель) яйца, анэнцефалия (полное или почти полное отсутствие мозга), гидроцефалия (избыток жидкости в мозге, наблюдаемый в виде уширения желудочков), спинальные (позвоночные) дефекты, такие как spina bifida, зачастую необнаружимые биохимическими методами, и дефекты желудочно-кишечного тракта. Вспомогательную, но очень важную роль играет ультразвук в процедуре амниоцентеза (пункции плодного пузыря)—взятии околоплодных вод для цитологических исследований и выявлении возможных генетических нарушений. Ввод иглы при амниоцентезе под контролем ультразвуковой визуализации, обеспечивает значительно большую безопасность этой процедуры.
Наконец, необходимо отметить ультразвуковое исследование движений плода. Это явление лишь недавно (с появлением эхоскопии в реальном времени) стало предметом подробного исследования. Сейчас происходит накопление большого количества информации как по движению конечностей плода и псевдодыханию (легкие плода заполнены жидкостью, так что «дыхание» здесь — сомнительный термин), так и по динамике сердца и сосудов. Здесь основной интерес представляет исследование физиологии и развития плода; до обнаружения аномалий плода пока еще далеко.
Может быть, из-за относительно малых размеров глаза (и, следовательно, возможности .работать в диапазоне частот выше тех, которые применяются при исследовании протяженных или глубоко залегающих органов) офтальмология несколько выделилась из прочих областей применения ультразвука.
Ультразвук особенно удобен для точного определения размеров глаза, а также для исследования патологии и аномалий структур глаза в случае их непрозрачности и, следовательно, недоступности для обычного оптического исследования. Здесь также важна точность работы и калибровки аппаратуры, необходимо также уделить особое внимание эффектам, связанным с преломлением ультразвука в хрусталике и роговице.
Область позади глаза — орбита — доступна ультразвуковому обследованию через глаз, поэтому ультразвук вместе с компьютерной томографией стал одним из основным методов неинвазивного исследования патологий этой области. Структуры орбиты имеют малые размеры и требуют хорошего пространственного разрешения и разрешения по контрасту, что достижимо на высоких частотах. Практические сложности могут возникать, однако, если пытаться использовать аппаратуру, характеристики которой заимствованы из телевизионной техники, а полоса пропускания соответственно ограничена.
8.9.3. ИССЛЕДОВАНИЕ ВНУТРЕННИХ ОРГАНОВ
Под таким заголовком можно рассмотреть множество разнообразных задач, в основном связанных с исследованием брюшной полости, где ультразвук используется для обнаружения и распознавания аномалий анатомических структур и тканей. Зачастую задача такова: есть подозрение на злокачественное образование и необходимо отличить его от доброкачественных или инфекционных по своей природе образований.

Рис. 8.6. В-изображения печени человека в сагиттальной плоскости: нефильтрованное (а) и фильтрованное с последующим подавлением когерентного спекл-шума путем адаптивной пространственной фильтрации (б) (Bamber J. С, в печати).
В этом смысле диагностическая ценность ультразвука растет параллельно с повышением качества систем визуализации, в частности в отношении разрешения по контрасту. Так, задачи по выявлению (диагностике) вторичных опухолей печени и дифференциации злокачественных и воспалительных изменений поджелудочной железы оказываются на пределе возможностей даже самых высококачественных систем, при этом даже небольшое повышение качества может значительно улучшить точность диагностики. Однако примечательно, что системы визуализации, работающие в режиме реального времени, даже если у них качество изображения хуже, чем у совершенных статических сканеров, также играют очень большую роль из-за своей гибкости, позволяющей обследовать пациентов со сложными и часто очень подвижными анатомическими структурами.
При исследовании печени (рис. 8.6) кроме важной задачи обнаружения вторичных (а иногда и первичных) злокачественных образований ультразвук полезен для решения других задач, включая обнаружение заболеваний и непроходимости желчных протоков, исследование желчного пузыря с целью обнаружения камней и других патологий, исследование цирроза и других доброкачественных диффузных заболеваний печени, а также паразитарных заболеваний, таких как шистосоматоз. Почки — еще один орган, в котором необходимо исследовать различные злокачественные и доброкачественные состояния (включая жизнеспособность после трансплантации) с помощью ультразвука или его комбинации с другими методами. Гинекологические исследования, в том числе исследование матки и яичников, в течение долгого времени являются главным направлением успешного применения ультразвука. Здесь зачастую также необходима дифференциация злокачественных и доброкачественных образований, что обычно требует наилучшего пространственного и контрастного разрешения. Аналогичные заключения применимы и к исследованию многих других внутренних органов и областей. Возрастает интерес к применению ультразвуковых эндоскопических зондов. Эти устройства, которые можно вводить в естественные полости тела (желудок, мочевой пузырь, прямую кишку и т. д.) при обследовании или применять при хирургическом вмешательстве, позволяют улучшить качество изображения из-за более высокой рабочей частоты и/или отсутствия на пути ультразвука таких неблагоприятных акустических сред, как газ или кость.
8.9.4. ПРИПОВЕРХНОСТНЫЕ И НАРУЖНЫЕ ОРГАНЫ
Щитовидная и молочная железы, хотя они и легко доступны ультразвуковому обследованию, часто требуют использования водяного и иного буфера, чтобы на изображение не повлияли аномалии ближней зоны поля. При исследовании щитовидной и (реже) паращитовидной железы основное применение ультразвука — различение кистозных и твердых образований, что возможно при хорошем подавлении шума и артефактов, вызванных реверберацией и боковыми лепестками излучателя.
Молочная железа — один из первых органов, на которых были сделаны попытки эхо-импульсного обследования [32]. Она легко доступна обследованию и, памятуя о распространенности ее заболеваний, остается только удивляться, что ультразвуковое обследование в этом случае еще не получило всеобщего распространения. Отчасти это можно объяснить деформируемостью и акустической неоднородностью данного органа, в котором значительные локальные отложения жировой ткани (обладающие относительно низкой скоростью звука, см. гл. 5) в процессе визуализации могут вызывать заметные аберрации, связанные с преломлением.
Основные задачи эхо-импульсного ультразвукового обследования молочной железы — различение твердых и жидких (кистозных) образований и различение разных типов твердых образований. Решение последней задачи требует особенно высокого пространственного и контрастного разрешения и в общем случае основывается на множестве диагностических критериев, включая форму границы поражения и тип акустического «затенения» (позитивное или негативное), которое является показателем соответствующих изменений коэффициента затухания ультразвука (рис. 8.7).
Захватывающая перспектива — скрининг для выявления самых ранних признаков рака молочной железы при отсутствии выраженных симптомов, особенно у женщин с аномально высоким фактором риска. Технически здесь необходимо обнаружить (без излишней доли ложно положительных решений) аномалию размером около 2 мм в диаметре (объемом 4 мм3) в объеме ткани порядка 105 мм3, когда эта аномалия относительно редко встречается в заданной группе, например, будет только у одной пациентки. Ясно, что это требует высочайшего разрешения по пространству и контрасту, а также умения правильно интерпретировать информацию во время обследования.
Методы визуализации молочной и щитовидной желез, часто использующие акустическую задержку распространения (водяной буфер), применимы также к обследованию других приповерхностных тканей, например, при измерении толщины кожи, необходимом в радиационной терапии для облучения электронами, при обследовании приповерхностных кровеносных сосудов, таких как сонная артерия, а также при исследовании реакции опухолей на терапевтические воздействия.
Рис. 8.7. В-изображения молочной железы, выполненные при сложном (а) и простом (б) режимах сканирования через водяной буфер. Карцинома видна и при простом сканировании после процедуры акустического улучшения (возможно, из-за аномально малого затухания) (из работы [14], с согласия Дж. Джеллинса).
Ультразвуковые методы широко применяются при обследовании сердца и прилегающих магистральных сосудов. Это связано, в частности, с возможностью быстрого получения пространственной информации, а также возможностью ее объединения с томографической визуализацией. Так, для обнаружения и распознавания аномалий движения клапанов сердца, в частности митрального, очень широко используется М-режим. При этом важно регистрировать движение клапанов вплоть до частот порядка 50 Гц и, следовательно, с частотой повторения около 100 Гц. Эта цифра, оставаясь значительно ниже упомянутого выше предела для эхо-импульсных приборов (около 5 кГц), в сущности недостижима при любых других методах исследований.
Применение М-режима в сочетании с визуализацией в реальном времени не только упрощает процесс поиска отдельных клапанов сердца и их частей, но также делает возможной визуализацию полного поперечного сечения сердца, выявление патологий сердечной мышцы (миокарда) и расчеты границ изменения во времени объемов различных камер сердца 1) (рис. 8.8). Для некоторых из этих задач становится существенным обеспечение хорошего контраста в кардиологических приборах, как и в случае приборов для абдоминальных исследований и других применений.
До появления рентгеновской компьютерной томографии мозг было особенно сложно исследовать. Начиная с 1951 г., в Лондонском королевском онкологическом госпитале (в настоящее время Королевский госпиталь Марсдена) предпринимались значительные усилия для применения ультразвука к этой задаче. К сожалению, этому мешают физические свойства черепа взрослого человека, поскольку череп представляет собой сильно поглощающую трехслойную структуру переменной толщины [30]. Хотя было сделано несколько интересных попыток преодолеть эти трудности, в том числе с использованием управляемых многоэлементных решеток, когда датчик прилегает к ограниченной области черепа, а также с частичной автоматической компенсацией фазовой задержки для учета изменений толщины черепа, такое применение не встретило одобрения диагностов. Однако еще не затвердевший череп плода или новорожденного в акустическом плане не представляет значительных преград, связанных с возникновением затухания или преломления, и поэтому ультразвуковое обследование здесь применяется все чаще.
1) Обработка эхограмм позволяет также проводить дифференциальную диагностику функционального состояния системы кровообращения (см.: Клиническая ультразвуковая диагностика: Руководство для врачей. В 2-х томах / Под ред. Н.М. Мухарлямова. — М.: Медицина, 1988, т. 1). Несколько в стороне по физическим принципам стоят разработанные в последние годы методы цветовой визуализации движения структур и кровотока (см.: Color Atlas of Real-Time Two-Dimensional Echography, ed. Ryozo Omoto, Shintan-To-Chiryo, Tokyo, 1984). — Прим. перев.
Рис. 8.8. Изображения работы сердца в режимах М и В: а — режим М и встроенное изображение типа В; направление локации в режиме М показано пунктиром на секторном B-изображении; б — полное секторное B-изображение с наложенным внизу сигналом ЭКГ. Представлено поперечное сечение сердца, расположенное, как показано на схеме в (Hewlett-Packard Journal, декабрь 1983 г.; публикуется с согласия фирмы «Хьюлетт-Паккард»).
Применение ультразвуковых эхо-импульсных методов приобрело огромное значение в различных областях медицины. Об этих методах много писалось с технической и клинической точек зрения, и они продолжают быстро развиваться. В этой главе была сделана попытка проанализировать некоторые из физических принципов этих методов и рассмотреть возможности и недостатки соответствующих систем в решении различных задач медицинской диагностики.
1. AIUM/NEMA (1983). Safety standard for diagnostic ultrasound equipment. J. Ultrasound Med. 2, SI—S50.
2. Alvisi, C. & Hill, C. R. (1980) Investigative ultrasonology II: Clinical advances, Tunbridge Wells, Pitman Medical.
3. Bamber, J. C. (1985) Adaptive filtering for reduction of speckle in ultrasonic pulse-echo images Ultrasonics 24, 41—44.
4. Bamber, J. C. & Dickinson, R. J. (1980) Ultrasonic B-scanning; a computer simulation. Phys. Med Biol. 25, 463—479.
5. Bom, H. (1977) Echocardiology. The Hague, Martinus Nijhoff.
6. Brendel, K. et al. (1976) Methods of measuring the performance of ultrasonic pulse-echo diagnostic equipment. Ultrasound in Med. and Biol. 3, 343—350.
7. Burckhardt, С. B. (1978) Speckle in ultrasound B-mode scans. IEEE Trans. SU25, 1—6.
8. Cosgrove, D. O., Garbutt, P. & Hill, C. R. (1978) Echoes across the diaphragm. Ultrasound Med. Biol. 3, 385—392.
9. DeVlieger, M. et al. (1978) Handbook of clinical ultrasound. New York etc. Wiley medical.
10. Foster, F. S. & Hunt, J. W. (1979) Transmission of ultrasound beams through human tissue—focusing and attenuation studies. Ultrasound in Med. and Biol. 5, 257—268.
11. Goldberg, В. B. & Wells, P. N. T. (1983) Ultrasonics in clinical diagnosis (3rd ed.) Edinburgh, Churchill—Livingstone.
12. Harder, D. (1981) Performance parameters of photographic imaging, In: Medical ultrasonic images: formation, displny, recording and perception. (C. R. Hill & A. Kratochwil, eds). Excerpta Medica, Amsterdam.
13. Hill, C. R. Carpenter D. A. (1976) Ultrasonic echo imaging of tissues: Instrumentation. Brit. J. Radiol. 49, 238—243.
14. Hill, C. R., McCready, V. R. & Cosgrove, D. O. (1978) Ultrasound in tumour dignosis. Tunbridge Wells, Pitman Medical.
15. International Electrotechnical Commission. (1986) Methods of measuring the performance of ultrasonic pulse-echo diagnostic equipment. (IEC Report no. 854), Geneva, IEC.
16. Kossoff, G. (1979) Analysis of focussing action of spherically curved transducers. Ultrasound in Med. and Biol. 5, 359—365.
17. Kurjak, A. (1980/1981) Progress in medical ultrasound: reviews and comments. Vol. 1 (1980), Vol. 2 (1981) Excerpta Medica, Amsterdam.
18. Kurjak, A. (1982) Progess in medical ultrasound: reviews and comments, Vol. 3 (1982) Excerpta Medica, Amsterdam.
19. Lypacewicz, G. & Hill, C. R. (1974) Choice of standard target for medical pulse-echo equipment evaluation. Ultrasound in Med. and Biol. 1, 287—289.
20. Magnin, P. A., Ramm, О. T. von, & Thurstone, F. L. (1982) Frequency compounding for speckle contrast reduction in phased array images. Ultrason. Imaging, 4, 267—281.
21. Meire, H. J. (1979) Diagnostic ultrasound (review). Brit J. Radiol. 52, 685—703.
22. Neary, R. J. (1981) Photographic imaging from CRT monitors, In: Medical ultrasonic images; formation, display, recording and perception (C. R. Hill & A. Kratochwil, eds.) Excerpta Medica, Amsterdam. 23.0'Donnell, M. (1982) Phase insensitive pulse-echo imaging. Ultrason. Imaging 4, 321—335.
24. Robinson,. D. E. & Knight, P. C. (1981) Computer reconstruction techniques in compound scan pulse-echo imaging. Ultrasonic Imaging 3, 217—234.
25. Smith, S. W. & Lopez, H. (1982) A contrast-detail analysis of diagnostic ultrasound imaging. Med. Phys. 9, 4—12.
26. Smith, S. W., Ramm, О. T. von, Haran, M. E. & Thurstone, F. L. (1979). Angular response of piezoelectric elements in phased array ultrasound scanners. IEEE Trans. SU26 185—191.
27. Somer, J. C. (1980) Optical signal processing in ultrasound In: Unvestigative ultrasonology 1: technical advances (C. R. Hill & C. Alvisi, eds) pp. 71—82. Pitman Medical, Tunbridge Wells, U. K.
28. Vogel, J., Bom, N., Ridder, J. & Lancee, C. (1979) Transducer design considerations in ultrasonic focussing. Ultrasound in Med. and Biol. 5, 187—193.
29. Wells, P. N. T. (1977) Biomedical ultrasonics, London, Academic Press.
30. White, D. N. et al. (1976) The effects of the skull upon the spatial and temporal distribution of a generated and reflected ultrasonic beam. Kingston (Canada), Ultrasmedison.
31. White, D. N. & Brown, R. E. (1977) Ultrasound in medicine. Volumes ЗА and 3B (Proc. 3rd World Congress of Ultrasound in Medicine and Biology). Plenum, New York.
32. Wild, J. J. (1978) The use of pulse-echo ultrasound for early tumour detection; history and prospects. In: Ultrasound in tumour diagnosis (C. R. Hill et al. eds) pp. 1—26. Pitman Medical, Tunbridge Well, UK.
ПРОЧИЕ МЕТОДЫ ВИЗУАЛИЗАЦИИ
К. Хилл
Прикладная акустика располагает широкими возможностями в области техники для визуализации, и это лучше всего оценить, читая труды ставших уже традиционными конференций [1]. Многие рассмотренные подходы могут найти применение в медицине и биологии, однако в целом область их применимости простирается значительно шире, захватывая подводные исследования и навигацию, геофизические исследования и контроль материалов. В медицине в настоящее время по применимости и доступности главенствует импульсная эхолокация (подробно описанная в гл. 8), а также импульсно-доплеровское обследование (гл. 11), представляющее значительный интерес для некоторых специальных приложений. В этой главе мы кратко опишем некоторые другие методы, которые разрабатываются в настоящее время и к которым появляется интерес в медицине и биологии. Как будет видно, в некоторых (хотя и не во всех) этих методах результирующее изображение является конформным отображением в пространстве изображения множества значений параметров отдельных участков объекта. В следующей главе мы расскажем о различных методах характериза-ции тканей — попытке определить дистанционно и in vivo некоторые локальные свойства биологической ткани, которые можно использовать для ее идентификации и выделения среди окружающих структур. Поскольку в принципе это тоже методы визуализации, деление материала между этой главой и гл. 10 весьма условно. В настоящей главе кратко описывается также акустическая микроскопия, которая, похоже, может найти замечательные применения в биологии. В основном методы акустической микроскопии сходны с обычными методами визуализации, но приспособлены для работы на высоких частотах, что обеспечивает высокое пространственное разрешение.
9.2. ДВУМЕРНАЯ РЕГИСТРАЦИЯ АКУСТИЧЕСКОГО ИЗОБРАЖЕНИЯ
Для осуществления некоторых способов визуализации, которые будут описаны в этой главе, требуются средства записи двумерного множества значений параметров акустического поля (амплитуды давления, фазы, времени прихода импульсов и т. д.). В принципе доступны многие методы, но практические требования к чувствительности по амплитуде, времени отклика и (в некоторых случаях) к чувствительности по фазе значительно ограничивают выбор. Основные методы акустической регистрации и измерения подробно рассмотрены в гл. 3, и последующее обсуждение призвано просто подчеркнуть некоторые аспекты, связанные с визуализацией.
Один из простейших методов записи двумерного множества значений параметров акустического поля — сканирование очень малым пьезоэлектрическим преобразователем над исследуемой поверхностью. Изображение может быть зарегистрировано без потери информации при условии, что размеры преобразователя, скорость съема данных и размеры растра выбраны так, чтобы получить наиболее богатое пространственными частотами акустическое поле, а динамический диапазон системы регистрации адекватен глубине модуляции поля.
Хотя эта процедура иногда и применяется, она слишком медленна для медицинских целей, и поэтому были созданы одно- и двухмерные решетки (матрицы) «точечных» преобразователей.
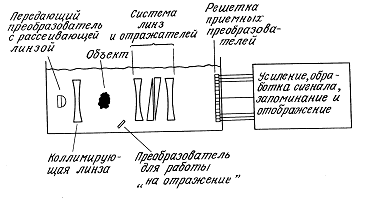
Рис. 9.1. Блок-схема системы трансмиссионной визуализации для применения в медицине.
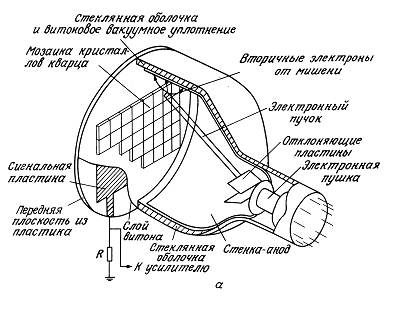
Рис. 9.2. Устройство звуковизора (а); трансмиссионное изображение кисти руки, помещенной вблизи передней поверхности камеры (б) [3].
Длину линейных решеток делают такой, чтобы перекрыть один из линейных размеров поля изображения, а для сканирования решеткой по полю (или полем по решетке) в поперечном направлении создается специальное приспособление [11]. Подобное устройство показано на рис. 9.1. Расширение такой решетки до двумерной может привести к непомерной сложности и стоимости, если используется обычная электроника, а требуется хорошая избирательность по пространственным частотам. Обсуждалась возможность построить такую решетку в виде твердотельного устройства, объединенного со своей собственной электроникой. Однако единственными изготовленными и применяемыми на практике устройствами являются различные варианты «звуковизора», или «трубки Соколова». Это аналог телекамеры, в которой внутренняя поверхность трубки покрыта пьезоматериалом, а распределение заряда на этой поверхности считывается сканирующим электронным пучком [3]. Конструкция и пример использования одного из таких звуковизоров представлены на рис. 9.2.
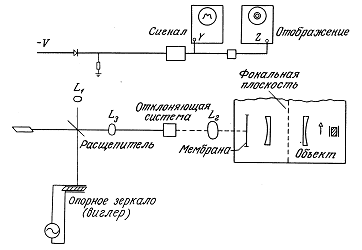
Рис. 9.3. Блок-схема интерферометрической ультразвуковой видеокамеры [21]. Применение такого устройства для точных измерений акустических полей описано в разд. 3.3.
Пьезоэлектрические приборы обладают тем неоценимым свойством, что их выходные сигналы являются электрическими, поэтому они очень широко применяются в устройствах акустической визуализации. Однако довольно успешно использовался и другой подход, связанный с наблюдением локальных деформаций границы раздела, ориентированной приблизительно нормально к направлению пучка. В одном из устройств этого типа (на которое уже были ссылки в разд. 3.3) используется граница раздела воздух/жидкость, на которой возникают стационарные деформации, соответствующие локальному значению радиационного давления, действующего на поверхность. В другом варианте устройства очень тонкая, отражающая свет пленка («мембрана») натянута поперек пучка, и с помощью методов оптической интерферометрии определяются локальные мгновенные значения смещения частиц в среде, через которую распространяется звук. Система такого типа [21] показана на рис. 9.3.
9.3. ТРАНСМИССИОННАЯ ВИЗУАЛИЗАЦИЯ
Исторически первые устройства медицинской ультразвуковой визуализации были акустическим аналогом обычной рентгенографической системы и позволяли регистрировать двумерную тень объекта. Подобный метод был впервые описан Дуссиком [8]; в качестве излучателя и приемника в работе использовались кристаллы кварца, а из-за отсутствия более удобных методов представления изображения и записи прохождение ультразвука через тонкий препарат мозга поточечно регистрировалось амперметром, отображающим усиленный сигнал приемного кристалла. Хотя в последующей работе Дуссика с соавт. [9] были представлены изображения, которые, как утверждалось, являлись контурами желудочков мозга, наблюдаемых через интактный череп, гораздо более вероятно, что они были порождены артефактами.
При таком способе визуализации возникают две физические проблемы. Первая из них (существенная, в частности, для вышеописанной внутричерепной визуализации) состоит в том, что неоднородность скорости звука в различных тканях может привести к рефракционным ошибкам. До некоторой степени эти трудности можно преодолеть, записывая только первый приходящий сигнал в каждой точке изображения: такая процедура предохраняет от непрямолинейности траекторий лучей [14]. Вторая проблема — когерентный спекл-шум, рассмотренный Грином и другими исследователями [13]. Они показали, что четкость трансмиссионных изображений конечностей и даже брюшной полости удивительно улучшается, когда в источник излучения ультразвука специально вносят пространственную и временную некогерентность. Пример такого трансмиссионного изображения приведен на рис. 9.2, б. Следует отметить, что, как и в эхо-импульсной визуализации, такие изображения в настоящее время можно получать как киноленту (так называемые изображения в реальном масштабе времени), что повышает их практическую и эстетическую ценность.
9.4. ТРАНСМИССИОННАЯ РЕКОНСТРУКТИВНАЯ ВИЗУАЛИЗАЦИЯ ПОЛЕЙ ЗАТУХАНИЯ И СКОРОСТИ ЗВУКА
Замечательные успехи рентгеновской реконструктивной визуализации, основанной на поглощении рентгеновских лучей, стимулировали попытки сделать то же самое с помощью ультразвука. При этом по массиву измеренных значений затухания ультразвука на различных трассах лучей восстанавливается томографическое изображение коэффициента затухания. Как и в случае простой трансмиссионной визуализации, описанной в предыдущем разделе, здесь также возникает проблема многолучевого прохождения, которую можно до некоторой степени преодолеть селективным приемом первого прошедшего сигнала. Однако все еще остается другая проблема, связанная с ошибкой из-за потери фазы сигнала (см. разд. 3.2).
Само существование заметной неоднородности скорости звука в ткани предполагает еще одну возможность ультразвуковой визуализации, отсутствующую у рентгеновских методов, а именно реконструкцию значений скорости звука (или обратной величины — коэффициента преломления). Этот подход кажется интересным, особенно в свете вышеизложенных проблем, возникающих при реконструкции распределения затухания, а также поскольку, по данным лабораторных измерений Бэмбера и Хилла [2], скорость звука можно использовать как индикатор патологии.
Основное ограничение любого вида трансмиссионной реконструктивной визуализации — это то, что ее невозможно применять для диагностики многих органов, когда кости или заполненные воздухом полости препятствуют распространению звука. Молочная железа — один из немногих органов, к которым эти ограничения не относятся и где практические попытки визуализации оказались успешными. На рис. 9.4 приведены два звуковых изображения молочной железы, полученные in vivo этим способом. Изображения ясно показывают наличие злокачественной патологии с одной стороны [10].
Рис. 9.4. Томографическое изображение молочной железы in vivo, полученное путем реконструкции по скорости звука: нормальной, после менопаузы (а) и с большой фиброаденомой (б) [10].
Особенность такой реконструктивной визуализации состоит в том, что, по крайней мере в принципе, реконструируемая величина (коэффициент затухания, скорость звука) может быть выражена в абсолютных единицах независимо от конкретных условий измерения и использована как объективная мера состояния исследуемого объема ткани (наличие патологии и т. д.). Кроме того, можно одновременно выделять две или более независимые величины и получать многопараметрические изображения, подобные полученным группой Гринлифа [12]. Кстати, эти изображения показывают интересные возможности применения цветового представления медицинской информации.
Способность получения карт скоростей звука в различных тканях открывает несколько интересных возможностей, кроме уже упомянутых, в частности возможность измерения локальных распределений температуры (например, в гипертермической терапии опухолей, см. разд. 13.5), а также возможность наблюдения потоков жидкости, так как скорость звука зависит как от температуры, так и от скорости среды.
9.5. ВИЗУАЛИЗАЦИЯ В РЕЖИМЕ ОБРАТНОГО РАССЕЯНИЯ С РЕКОНСТРУКЦИЕЙ ПО ДВУМ ПАРАМЕТРАМ
В предыдущей главе было отмечено, что эхо-импульсная визуализация в традиционном варианте принципиально не является количественным методом в том смысле, что амплитуда эхо-сигнала зависит от двух параметров — коэффициента затухания и коэффициента обратного рассеяния, которые с помощью этого метода разделить нельзя.
Разделение этих переменных — одна из особенностей реконструктивной визуализации. Хотя, по крайней мере в медицине, до сих пор реконструктивная томография почти без исключения основывалась на данных, полученных трансмиссионным методом, эта концепция является более общей и, в частности, применима к данным, полученным при обратном рассеянии (рис. 9.5). Такой подход разрабатывался для раздельной регистрации коэффициентов затухания и обратного рассеяния по данным измерения только обратного рассеяния. Применимость этого способа в диагностике гораздо шире, чем у трансмиссионного метода. В предварительных исследованиях Дак и Хилл [5, 6] показали, что и теоретически, и практически возможно получать такие изображения, которые, с одной стороны, позволяют правильно устанавливать компенсирующее усиление на эхограмме (при этом изображение становится количественно пред-ставимым и воспроизводимым, так что уровень амплитуды отображения коррелирует не с местоположением, а с конкретной гистологией), с другой — независимо получать изображение по затуханию. Трудности реализации этого метода, однако, значительны и заключаются не только в сложности требуемых вычислений, но также и в выполнении измерений и обработки данных таким способом, чтобы было правильно учтено воздействие дифракционного расплывания и рефракции на измеряемый акустический сигнал.
Существует еще один оригинальный подход, теоретические основы которого уже описаны в общих чертах в гл. 6, — метод дифракционной томографии [19, 20]. Это попытка по наблюдаемому рассеянию ультразвука восстановить пространственное распределение в исследуемом объекте механических свойств, таких как плотность и модуль сжимаемости. Однако пока этот метод может применяться лишь для относительно простых структур, и его использование в случае сложных биологических структур (без использования статистической модели) кажется весьма отдаленной перспективой.
Рис 9.5 Схемы реконструкции при количественной ультразвуковой визуализации. Трансмиссионная реконструкция по затуханию (аналог рентгеновской компьютерной томографии): интенсивность прошедшей волны
используется для вычисления распределения коэффициента затухания (по известному набору элементов объекта -пикселов) (а). Времяпролетная трансмиссионная реконструкция: время прихода Tt излученного импульса используется для вычисления распределения скорости звука (по известному набору элементов) (б). Реконструкция в режиме рассеяния: интенсивность рассеянного сигнала![]() , под заданным углом в используется для вычисления как сечений рассеяния, так и распределения коэффициента затухания по известному набору элементов объекта (в). Реконструкция по обратному рассеянию представляет собой частный случай «в».
, под заданным углом в используется для вычисления как сечений рассеяния, так и распределения коэффициента затухания по известному набору элементов объекта (в). Реконструкция по обратному рассеянию представляет собой частный случай «в».
Понятие голографии хорошо известно в оптике, где этот термин был введен Табором в смысловом значении «полная картина», т. е. изображение, содержащее информацию как об амплитуде, так и о фазе волн. В оптике развитие метода, с помощью которого можно легко зарегистрировать такую полную информацию об объекте и использовать ее для восстановления изображения, было огромным достижением и вскоре навело на мысль, что сходный метод можно применить и к акустике. Начиная примерно с 1965 г. было выполнено значительное количество работ в этом направлении и большая их часть описана в литературе, в частности в трудах нескольких конференций по этой тематике [1] и в обзорах, таких например, как превосходная работа Чиверса [4].
Логика перенесения принципа голографии в акустику требует тщательного анализа. Основное отличие от оптики состоит в том, что в акустике нетрудно получать и регистрировать фазовую информацию одновременно с амплитудной, так как всегда можно брать выборки в нужном частотном диапазоне. Все дело в том, что записывать только амплитуду проще и дешевле. На практике, в некоторых методах визуализации и характеризации тканей (см. гл. 10), применяется традиционное оборудование для приема и дальнейшего использования таких полных наборов данных. В этом смысле идея голографии является естественной для акустики, и привлекать какие-либо особенные тонкости этого предмета не требуется.
Второе важное отличие акустической голографии от оптической связано с доступностью аппаратурной реализации. Оптические голограммы обычно формируются как картины интерференции между модулированным (объектным) и опорным пучками в плоскости фотоэмульсии. Отсутствие простого акустического аналога фотоэмульсии может вызвать значительные технические сложности, и большинство широко используемых акустических методов записи таких голограмм используют пространственные картины левитации поверхности жидкости на границе вода/воздух, которые последовательно считываются сканирующим лучом лазера (см. раз. 9.6). Другой метод — непосредственное сканирование волнового фронта акустоэлектрическим преобразователем (или решеткой преобразователей, ср. рис. 9.1), при котором акустический опорный пучок не требуется, а может быть заменен опорным значением фазы в электрической форме. Пример такой фазовой интерферограммы будет приведен ниже при обсуждении акустической микроскопии (см. рис. 9.8).
Дополнительные проблемы в акустической голографии возникают при восстановлении изображений. Изображение в оптической голографии обычно восстанавливается с использованием излучения (видимого света) с той же длиной волны, что и при записи, тогда как в акустической голографии (за исключением, может быть, акустической микроскопии на гиперзвуковых волнах; см. раз. 9.7) восстановление в видимом свете приводит к смещению длины волны на 2—3 порядка с пропорциональным сокращением размеров изображения. Хотя это и препятствует качественному восприятию трехмерности изображения, однако не мешает в принципе регистрировать изображение в трех измерениях и затем отображать любую выбранную плоскость. На эту возможность влияет, однако, то, что сигналы вне выбранной плоскости вносят неизбежный вклад в шум изображения, на который накладывается спекл-шум, особенно интенсивный из-за требования узкополосности спектра в голографии.
Таким образом, пока акустическая голография — это интригующая идея, предлагающая некоторые возможности трехмерной визуализации внутренних органов человека. Однако прямые параллели с оптическим аналогом наталкиваются на несколько серьезных физических ограничений. Реальное значение голографии в медицине будущего, по-видимому, связано с более широким толкованием принципа одновременного использования фазовой и амплитудной информации.
Способность генерировать и улавливать акустическую энергию на очень высоких частотах и соответственно малых длинах волн открыла возможность создания методов акустической микроскопии. Эта идея была впервые исследована в 1936 г. Соколовым, который использовал описанный выше прототип ультразвуковой видеокамеры (звуковизора). Другой подход с использованием тонкопроволочной термопары в качестве сканируемого детектора был описан позднее Данном и Фраем [7]. Ни один из этих интересных подходов не смог обеспечить необходимую комбинацию чувствительности и пространственного разрешения для реализации всех физических возможностей этой методики и только с 1970 г. начались систематические исследования в этой области. Превосходный детальный обзор сделали Лемонс и Куэйт [17].
Как уже отмечалось в предыдущих разделах этой главы, существует много возможных подходов к проблеме акустической визуализации, многие из которых сейчас применяются в форме «микроскопии». Особое внимание уделялось трансмиссионной технике при работе с объектами в виде тонких срезов (аналогично оптической микроскопии). Возрастает также интерес к информации, полученной при отражении и рассеянии. В трансмиссионной визуализации различают методы, дающие прямое изображение акустического поля, «модулированного объектом» (например, с использованием приборов типа ячейки Польмана, см. гл. 3), которое можно непосредственно наблюдать или фотографировать, и методы получения изображений пошаговым сканированием. Первая группа методов пока применяется относительно безуспешно, и сейчас всюду используются сканирующие методы, обладающие рядом существенных преимуществ. Среди сканирующих методов можно также выделить две большие группы: во-первых, методы, в которых модулированное акустическое поле регистрируется в ближней зоне объекта, т. е. на расстояниях, сравнимых с пространственным разрешением системы, и, во-вторых, методы регистрации в дальней зоне на гораздо больших расстояниях.
Пример системы с регистрацией в ближней зоне, предложенной Кесслером [16], показан на рис. 9.6, где модулированное акустическое поле измеряется по смещению, вызванному этим полем на оптически зеркальной поверхности, помещенной приблизительно нормально к направлению пучка. Объект погружен в жидкость (например, в воду), верхняя граница которой соприкасается с оптически полуотражающей плоской поверхностью твердого прозрачного блока. Амплитуды и фазы смещений этой поверхности связаны с коэффициентом затухания и скоростью звука в прилегающих снизу областях объекта и могут быть измерены с помощью сканирующего оптического (например, лазерного) пучка. Обычно лазерный пучок можно сканировать в стандартном видеорастре, получая изображение в «реальном времени». Важным свойством этой установки является возможность одновременного получения оптического изображения объекта с помощью фотодиода, расположение которого показано на рисунке.
Относительная апертура и, следовательно, эффективная разрешающая способность такой системы на заданной частоте ограничивается критическим углом отражения ультразвука на оптически отражающей поверхности. Желательно подобрать отношение скоростей звука в иммерсионной жидкости и твердом теле как можно ближе к 1, поэтому в качестве материала для верхнего блока выбирается специальная пластмасса.
Рис. 9.6. Принцип действия сканирующего лазерно-акустического микроскопа [16].
На практике достигнуто разрешение порядка 10 мкм (т. е. полторы длины волны в воде) на частоте 220 МГц. Ниже этого предела могут проявляться ограничения оптической системы, в том числе размер лазерного пятна. При небольшой модификации стандартной системы, когда угол падения акустического пучка на отражающий блок устанавливается равным критическому, — устанавливается режим «темного поля». На рис. 9.7 показаны примеры изображений (акустического поглощения и акустической фазовой интерферограммы), полученных с помощью сканирующего лазерно-акустического микроскопа Кесслера (СЛАМ).
В последнее время все возрастающий интерес, отчасти вызванный работой Куэйта с соавт. из Станфордского университета, вызывает создание систем, работающих в дальней зоне. Базовая установка такой системы (сканирующего акустического микроскопа — САМ) показана на рис. 9.8. Излученная плоская волна фокусируется линзой в фокальное пятно на тонком объекте, а промодулированная объектом волна собирается такой же линзой на приемной системе.

Рис. 9.7. Трансмиссионные акустические микрофотографии распределений поглощения (а) и интерференции (б), полученные на сканирующем лазерно-акустическом микроскопе, работающем в ближнем поле на частоте 100 МГц; изображен тонкий неокрашенный срез (0,5 мм) опухоли печени (метастазирующая аденокарцинома). Видны сечения коллагеновых перегородок, окружающих группы опухолевых клеток, часть которых имеет некротические центры и, видимо, поэтому сильнее поглощает ультразвук. На интерференционной микрофотограмме видны полосы, боковое смещение между которыми пропорционально локальной скорости звука в образце (приводятся с согласия д-ра Р. Ваага, Рочестерский университет, и д-ра Л. Кесслера, «Соноскан Инк.»).
Рис. 9.8. Принцип действия сканирующего акустического микроскопа (САМ) в стандартном трансмиссионном режиме. Принципиально осуществимы другие режимы работы, например стереоскопия, режимы «темного поля», отражения и т. д.
Изображение получается путем сканирования объекта в его собственной плоскости и регистрации соответствующих значений амплитуды и фазы.
Очень интересная особенность оптического элемента в такой акустической системе заключается в том, что можно построить систему, в которой линза и иммерсионная жидкость имеют очень разные скорости распространения (например, в акустике отношение скоростей ультразвука для системы вода — сапфир равно 0,135, тогда как в оптике для системы стекло — воздух оно равно 0,66). Можно показать, что при этом сферические аберрации в акустике пренебрежимо малы даже при большой относительной апертуре. Это в принципе обеспечивает очень высокую разрешающую способность, на практике ограниченную коэффициентом затухания и скоростью звука в иммерсионной жидкости. Полезно определить показатель качества М такой жидкости (нормированный по отношению к воде), который характеризует потенциальную разрешающую способность прибора с заданной геометрией и акустоэлектри-ческими характеристиками:
где cw, с — скорости звука в воде и иммерсионной жидкости, ![]() — соответствующие коэффициенты затухания, нормированные на квадрат частоты.
— соответствующие коэффициенты затухания, нормированные на квадрат частоты.
Для большинства молекулярных жидкостей М < 1; более высокие его значения — для ртути (1.89), жидкого азота (2,1) и жидкого гелия (3,6) [17]. Недавно [23] было показано, что микроскопы, работающие со сжатым аргоном или ксеноном, характеризуются значениями М~5. При этом предсказанное разрешение на частоте 740 МГц и давлении ксенона 4 МПа (или 40 бар) составляет 0,17 мкм, что значительно превосходит предельные значения для обычных оптических микроскопов. Примеры акустических микрофотографий, полученных с помощью водно-иммерсионного микроскопа на частоте 900 МГц, показаны на рис. 9.9.
Структура базового САМ, описанная здесь, очень гибкая и допускает множество модификаций. Так, например, если ось приемной линзы и преобразователя смещена на 10—20° от оси излучающей системы, то установка начинает работать в режиме «темного поля», в котором регистрируются только рассеянные волны. Применяя достаточно быстродействующую электронику в приемном тракте, эту систему можно использовать как импульсный эхолокатор с одним преобразователем, в частности, для исследования особенностей поверхности исследуемого объекта и приповерхностного слоя. Наконец, излучая (в исходной системе с двумя преобразователями) сигнал на одной частоте (например, 450 МГц) и настраивая приемник на вторую гармонику (900 МГц), можно получить изображение, характеризующее нелинейные акустические свойства объекта и/или иммерсионной среды [17] (см. рис. 9.9).
Хотя высокое пространственное разрешение само по себе является заманчивым преимуществом акустической микроскопии, еще более существенно то, что она дает совершенно другую информацию по сравнению с оптическими микроскопами. Контраст в акустической микрофотографии возникает вследствие различия упругих характеристик материалов (в частности, акустических коэффициентов поглощения и скоростей звука).
Рис. 9.9. Акустические трансмиссионные микрофотограммы препарата ткани почки, полученные с помощью сканирующего акустического микроскопа: на частотах 450 МГц (а) и 900 МГц (б); на второй гармонике при излучении 450 МГц и приеме на 900 МГц формирование изображения, по-видимому, происходит благодаря изменениям нелинейности среды распространения ультразвука в объекте (в) [17].
И хотя о свойствах биологических сред на высоких (гиперзвуковых) частотах известно довольно мало, оказывается, что на практике контраст акустического изображения может быть намного выше, чем у оптического изображения неокрашенных препаратов. Таким образом, акустические микрофотографии могут давать новую информацию и быть полезными при обследовании живых клеток и тканей. Они могут также нести полезную информацию о природе акустических неоднородностей, вызывающих рассеяние (см. гл. 6), которое широко применяется в традиционной акустической эхо-импульсной визуализации (гл. 8), а также с недавнего времени в некоторых методах характеризации тканей (гл. 10). В этом смысле основной акцент в акустической микроскопии должен ставиться не столько на высоком пространственном разрешении, сколько на количественной оценке пространственного распределения упругих свойств различных тканей.
1. Acoustical Holography/Acoustical Imaging (1967) Series of conference proceedings. Plenum, New York.
2. Bamber, J. C. & Hill, C. R. (1981) Acoustic properties of normal and cancerous human liver, I: dependence on pathological condition. Ultrasound Med. Biol. 7, 122—133.
3. Brown, P. H., Randall, R. P., Fiyer, R. F. & Wardley, J. (1975) A high resolution, ultrasounic image converter, in Ultrasonics International 1975 Conference Proceedings, pp. 73—79, Guildford, IPC Science and Technology Press.
4. Chivers, R. C. (1977) Acoustical holography, In: Recent advances in ultrasound in biomedicine, 1, pp. 217—251 (ed. D. N. White). Research Studies Press, Forest Grove, Ore. U.S.A.
5. Duck, F. A. & Hill, C. R. (1979a) Mapping true ultrasonic backscatter and attenuation distribution in tissue: a digital reconstruction approach, in Ultrasonic tissue characterization II (ed. M. Linzer), NBS Special Publication 525, pp. 247—251, Washington, D. C, US Govt. Printing Office.
6. Duck, F. A. & Hill, C. R. (1979b) Acoustic attenuation reconstruction from backscattered ultrasound, in Computer aided tomography and ultrasonics in medicine, (ed. Raviv et al.)> North Holland Publishing Co.
7. Dunn, F. & Fry, W. J. (1959) Ultrasonic absorption microscope. J. acoust. Soc. Amer. 31, 632—633.
8. Dussik, К. T. (1942) Uber die Moglichkeit, hochfrequente mechanische Schwingungen als diagnostisches Hilfsmittel zu verweten. Z. ges Neurol. Psych. 174, 153—168.
9. Dussik, К. Т., Dussik, F. & Wyt, L. (1947) Auf dem Wege zur Hypophonographie des Gehirnes. Wien. Med. Wochenschr. 97, 425—429.
10. Glover, G. H. (1977) Computerized time of flight ultrasonic tomography for breast examination. Ultrasound in Med. and Biol. 3, 117—127.
11. Green, P. S., Schaefer, L. F., Jones, E. D. & Suarez, J. R. (1974) A new high-performance ultrasonic camera in Acoustic Holography, Vol. 5. (ed. P. Green) pp. 493—503, New York, Plenum Press.
12. Greenleaf, J. F., Kenue, S. K., Rajagopalan, В., Bahn, R. C. & Johnson, S. A. (1980) Breast imaging by ultrasonic computer-assisted tomography, In: Acoustical imaging, Vol. 8 (ed. A. F. Metherell) pp. 599—614. New York, Plenum Press.
13. Havlice, J. F., Green, P. S., Taenzer, J. C. & Mallen, W. F. (1977) Spatially and temporally varying insonification for the elimination of spurious detail in acoustic transmission imaging. In: Acoustical holography, Vol. 7, (ed. L. W. Kessler) pp. 291—305, New York, Plenum Press.
14. Heyser, R. C. & Le Croissette, D. H. (1974) A new ultrasonic imaging system using time delay spectrometry. Ultrasound in Med. and Biol. 1, 119—131.
15. Hill, C. R. (1976) Ultrasonic imaging: review article. J. Physics E: Scientific Instruments 9, 153—162.
16. Kessler, L. W. (1974) Review of progress and applications in acoustic microscopy. J. acoust. Soc. Amer. 55, 909—918.
17. Lemons, R. A. & Quate, C. F. (1979) Acoustic Microscopy, in Physical acoustics, Vol. 14 (ed. W. P. Mason & R. N. Thurston), pp. 1—91, New York, Academic Press.
18. Marich, K. W, Zatz, L. M., Green, P. S., Suarez, J. R. and Makovski, A. (1975). J. Clin. Ultrasound 3, 5—16.
19. Mueller, R. K. (1980) Diffraction tomography I: The wave equation. Ultrasonic imaging 2, 213—222.
20. Mueller, R. K., Kaveh, M. & Iverson, R. D. (1978) A new approach to acoustic tomography using diffraction techniques, In Acoustical imaging, Vol. 8 (ed. A. Metherell). pp. 615—628, New York, Plenum Press.
21. Vilkomerson, D., Mezrich, R. & Etzold, K. F. (1977) An improved system for visualizing and measuring ultrasonic wave fronts, In: Acoustical Holography, Vol. 7 (ed. L. W. Kessler), pp. 87—101, New York, Plenum Press.
22. Wade, G. Elliot, S., Khogees, I., Flesher, E., Eicher, J., Menza, D., Ramesh, N. S.
& Heidbreder, G. (1980) Acoustic echo computer tomography. In: Acoustical imaging Vol. 8 (ed. A. F. Metherell) pp. 565—576, New York, Plenum Press.
23. Wickramasinghe, H. K. & Petts, C. R. (1980) Gass Medium acoustic microscopy, In: Scanned image microscopy (ed. E. A. Ach), pp. 57—70, London, Academic Press.
ТЕЛЕГИСТОЛОГИЯ
К. ХИЛЛ
Методы получения изображения в медицине делятся на три широкие, но взаимно связанные группы, которые можно обозначить как «теневые», «эмиссионные»1) и «томографические». Исторически первыми стали использовать теневые методы — рентгеновские, а затем ультразвуковые. В начале 50-х годов появились эмиссионные методы с применением радиоизотопов (позже — инфракрасного излучения) и ультразвуковая томография. Из трех перечисленных групп лишь томографические методы (прямые, такие как обычное ультразвуковое В-сканирование, или компьютерная реконструкция) обеспечивают однозначную связь между объектом и элементами изображения, что позволяет надеяться на получение информации для распознавания или характеризации тканей. Обычные рентгеновские или радиоизотопные изображения, конечно, тоже полезны для характеризации отдельных участков тканей, но только с учетом прямой или косвенной априорной информации об анатомическом строении исследуемой области.
Не случайно появление терминов «характеризация тканей» и «телегистология» (дистанционное исследование тканей) совпало по времени с бурным развитием методов реконструктивной рентгеновской томографии и ультразвукового сканирования (начало 70-х годов). Действительно, визуализацию и телегистологию можно рассматривать как два взаимно дополнительных аспекта исследования. Здесь, как в соотношении неопределенностей Гейзенберга, существует связь пространственной разрешающей способности (возможности различать два соседних структурных элемента) с количеством информации, достаточным для отнесения этих элементов к той или иной «гистологической» категории. В визуализации проявляется одна крайность этой связи, а в телегистологии — другая.
1)Более удачный термин «радиография» уже используется в другом смысловом значении. На практике различие между тремя группами стирается с появлением реконструктивных вычислительных устройств, с помощью которых данные, полученные первым или вторым методом, могут быть обработаны для построения томограммы, т. е. двумерного изображения выбранного среза объекта.
Отсюда ясно, что большая часть необходимой информации о телегистологии уже изложена в двух предыдущих главах. Важно подчеркнуть, что телегистология, пусть в неявном виде, составляет существенную часть задачи специалиста по ультразвуковой диагностике, пытающегося понять происхождение какого-либо участка изображения на основании анализа амплитуд эхо-сигналов, структуры эхограмм, характера затенений и других признаков. Далее в этой главе мы рассмотрим физические и технические средства, с помощью которых можно расширить диагностические возможности и чувствительность такого метода.
Суть телегистологии заключается в описании определенной области ткани или органа совокупностью признаков, т. е. такими свойствами объекта или его изображения, которые можно измерить количественно дистанционными методами (в данном случае — ультразвуковыми). Здесь термин «количественно» включает в себя и двоичную классификацию (типа плюс — минус).
В следующих разделах мы обсудим некоторые из этих признаков. Можно придумать различные схемы их классификации, и ни одна из них не будет единственно логичной, но здесь мы будем рассматривать их в следующем порядке: физические признаки исследуемой ткани, признаки изображения, признаки рассеяния и признаки движения тканей. Признак может быть интуитивно понятным, например, это может быть признак границ в изображении или скорость звука в материале. Но признаком может быть и величина, определяемая из статистических или других свойств ансамбля данных, и поэтому, по крайней мере для большинства исследователей, не иметь очевидного интуитивного толкования.
Для решения частной диагностической задачи, например для различения нормальной и пораженной циррозом печени, можно использовать несколько признаков. Их часто называют «дискриминаторами» или «отличительными признаками» для обозначения их использования в рамках конкретной задачи и измерительной системы. Например, для решения указанной задачи различения в качестве дискриминаторов можно использовать среднюю амплитуду эхо-сигнала, плотность (пространственную частоту) текстуры изображения и наклон ВАРУ (см. разд. 8.1). Последний используется для получения однородного изображения и позволяет получить приближенное значение коэффициента затухания. Очевидно, что в данном определенном контексте одни дискриминаторы будут лучше других (хотя сами по себе признаки не являются плохими или хорошими), а их ценность будет зависеть от нескольких факторов. Во-первых, дискриминатор может не полностью коррелировать с гистологическими различиями, например, не все цирротизированные ткани обладают более высоким затуханием, чем нормальные. Во-вторых, в любой измерительной системе имеются шумы (большие или малые), что приводит к перекрытию результатов измерения в норме и патологии, хотя сами по себе множества признаков могут быть физически разделимыми. В-третьих, ценность дискриминатора может зависеть от того, используется ли он для абсолютных или для относительных оценок. Так, абсолютные измерения средней амплитуды эхо-сигнала малопригодны в качестве дискриминатора цирроза печени из-за различия затухания в коже у разных пациентов, но сравнительные измерения в коре близлежащей почки в качестве эталона могут оказаться весьма полезными.
После накопления достаточного опыта в тех или иных конкретных применениях телегистологии становится возможным приписать, каждому из используемых дискриминаторов свой вес. При комбинированном использовании нескольких дискриминаторов (см. рис. 7.6) и особенно в случаях, когда их весовые соотношения изменяются, необходимо применять методы многофакторного анализа для их оптимального использования. В дальнейшем станет ясно, что существует много дискриминаторов, пригодных для решения данной конкретной задачи, но только некоторые из них могут быть строго независимыми.
До сих пор отсутствует литература с систематизированными результатами по ультразвуковой телегистологии, хотя в обзорах и трудах конференций имеется большое число работ [1, 10, 25] по этому вопросу. Недавно появившиеся ежегодные обзоры [4, 5, 26] могут ознакомить читателя с новейшими публикациями в этой области.
10.2. ИСПОЛЬЗОВАНИЕ ОБЪЕМНЫХ ХАРАКТЕРИСТИК ИССЛЕДУЕМОЙ ТКАНИ
Как показано в предыдущих главах, дистанционными методами в принципе можно измерить несколько объемных акустических параметров тканей: коэффициент затухания ![]() (гл. 4), коэффициент обратного рассеяния
(гл. 4), коэффициент обратного рассеяния ![]() (гл. 6), скорость звука с (гл. 5), удельный акустический импеданс z (разд. 1.7 и 6.6). Кроме того, можно измерять и использовать в качестве дискриминаторов, например, зависимость
(гл. 6), скорость звука с (гл. 5), удельный акустический импеданс z (разд. 1.7 и 6.6). Кроме того, можно измерять и использовать в качестве дискриминаторов, например, зависимость ![]() и
и ![]() от частоты или зависимость с от температуры.
от частоты или зависимость с от температуры.
Методы количественного определения затухания, коэффициента обратного рассеяния и скорости звука рассмотрены в гл. 9 при описании реконструктивной визуализации. Сравнительно мало известно об этих величинах как о дискриминаторах, хотя несколькими группами исследователей была обнаружена корреляция между возрастанием скорости звука и возникновением злокачественных новообразований в молочной железе, что, вероятно, сопровождается замещением жировой ткани тканью, содержащей большее количество воды (см. гл. 5). Однако, как уже отмечалось, применение этих параметров для целей телегистологии представляется перспективным, так как они являются основой измерений «затенения», «наклона ВАРУ» (затухания) и «среднего уровня эхо-сигналов» (обратного рассеяния). Возможно также, что некоторые из эффектов, описываемых как затенение, могут быть отчасти обусловлены явлениями преломления, фокусировки и дефокусировки, связанными с прохождением ультразвукового пучка через области с неоднородной скоростью звука.
Удельный акустический импеданс может применяться на практике как дискриминатор, а соответствующий метод измерений называется «импедниграфией» (см. разд. 6.6). Вероятно, идея метода была заимствована из геофизики, где по фазовым и амплитудным соотношениям в эхо-сигнале, принятом от простых, почти плоских гладких структур, можно аналитически восстановить изменения импеданса на границах. Вероятно также, что этот метод применим для исследования организма человека лишь в крайне редких случаях, когда объектом диагностики являются почти плоские границы. В настоящее время эти методы еще не применяются в практике, хотя ведутся интересные теоретические исследования более общих моделей.
10.3. ИСПОЛЬЗОВАНИЕ ПРИЗНАКОВ ЭХОГРАММЫ
Для получения эхограммы необходимо вначале принять эхо-сигналы на несущей частоте, т. е. в недетектированном виде, а затем преобразовать их в видеосигналы, которые можно достаточно просто запомнить и отобразить наряду с информацией о пространственном расположении линии сканирования. В этом разделе мы рассмотрим использование признаков, получаемых на основе подобных данных.
Чтобы использовать на практике такой способ характеризации тканей, необходимо иметь устройство стробирования, оцифровки и запоминания больших массивов данных с частотой порядка 10 МГц, а также компьютер, способный обрабатывать данные со скоростью, приемлемой для клинического обследования. Такая аппаратура стала доступной не так давно, однако некоторые ранние работы по этой тематике были выполнены вручную [16]. Вычислялась амплитудная гистограмма А-эхограммы по частоте появления всплесков заданной амплитуды в эхо-сигнале. Было показано, что средняя амплитуда эхо-сигнала может служить полезным дискриминатором для различения циррозной печени от здоровой.
Однако на амплитуду эхо-сигнала сильно влияет изменяющееся затухание в вышележащих слоях тканей, поэтому все больший интерес проявляется к дискриминаторам, основанным на измерении пространственных признаков изображения или связанных с ним параметров, например в недектированном эхо-сигнале. Здесь возникает интересное расхождение взглядов. С одной стороны, имеется «строгий» подход: для анализа необходима исчерпывающая информация на несущей частоте ультразвука, так как детектирование неизбежно влечет за собой потерю информации о фазе и, возможно, приводит к некоторому уменьшению полосы частот. Главная сложность при этом заключается в том, что запоминание изображения в радиочастотной форме до проведения анализа требует специальных приемов и аппаратуры, которых не имеется в стандартных эхо-импульсных системах. Поэтому до настоящего времени этот подход ограничивался анализом лишь одномерных (типа А), а не двумерных (типа В) изображений.
Противоположный «практический» подход — анализировать данные В-сканирования, представляемые в обычной форме видеосигнала. Однако здесь тоже могут появиться сложности, связанные, например, с тем, что количество поступающей информации как по динамическому диапазону, так и по пространственной частоте дискретизации (особенно в продольном направлении), даже после детектирования может значительно превышать емкость цифровой памяти, применяемой в современных серийных В-сканерах.
В описанных выше случаях задача нахождения диагностически информативных дискриминаторов имеет много общего с другими методами анализа сигналов и изображений, применяемыми например, в аэрофоторазведке или в микробиологии. Однако здесь надо принимать во внимание особое обстоятельство — наличие когерентного спекл-шума (см. разд. 6.5.2) в изображении и в А-эхограмме, а также фонового шума, которые могут понижать качество по крайней мере некоторых из дискриминаторов.
Весьма полезное сообщение об использовании анализа текстуры тканей по А-эхограмме на несущей частоте ультразвука приведено в работе [8]. Для различения in vivo ткани нормальной печени (n) и тканей с двумя диффузными патологиями — ожирением печени (f) и алкогольным циррозом (с), что вызывает постановку трех задач различения: n/f, n/с и f/c, применялся набор из 16 дискриминаторов, основанных на статистических данных. Для всех перечисленных задач различения была установлена статистическая значимость каждого из 16 дискриминаторов в разделении нормы и патологии. Затем с помощью многофакторного анализа была изучена возможность комбинированного анализа нескольких дискриминаторов, и оказалось, что оптимальная способность различения тканей достигается при совместном анализе примерно четырех из них. Однако более поздняя работа тех же авторов ставит под сомнение полученные результаты.
В этой работе авторы исследовали, как на способность различения влияет детектирование исходных данных (путем цифровой, т. е. как бы «идеальной», обработки). Они показали, что при этом может происходить некоторая потеря способности различения [9], хотя им и не удалось установить, происходит ли эта потеря из-за существенного уменьшения объема данных (что может быть скомпенсировано значительно более представительной выборкой при анализе В-изображения) или она обусловлена более существенной причиной, связанной с потерей полосы частот [7].
Пример другого подхода к анализу В-изображений содержится в работе [23], в которой исследуемая область изображения выделяется и запоминается, затем по ней вычисляется несколько текстурных признаков и используется комбинация этих признаков для характеризации области. Эти признаки разделяются на несколько видов и включают в себя 6 статистических характеристик распределения вероятности амплитуды сигнала по всем точкам выбранной области, 5 характеристик пространственной плотности эхо-сигналов, 13 характеристик производной по пространству изображения, 21 характеристику двумерного фурье-преобразования изображения и 48 статистических характеристик 2-го порядка, определяемых путем построения матриц совпадения событий. Эти признаки анализируются совместно с помощью пакета программ статистической обработки, при этом можно выделять «наилучший» для данного изображения набор дискриминаторов, а затем применять выбранную процедуру для классификации неизвестных данных. Показано, что эту процедуру можно применять для решения целого ряда клинических задач, например для обнаружения и классификации диффузных заболеваний печени и опухолей брюшной полости [19, 20], а также для контроля за реакцией опухолей и окружающих нормальных тканей на лечебное воздействие (рис. 10.1).
Чтобы уменьшить потери информации в изображении, сохранив совместимость разработанной системы со стандартной аппаратурой для визуализации, эти авторы использовали аналого-цифровой преобразователь для временного запоминания изображения, предоставив врачу возможность выбрать одну или несколько ограниченных областей изображения для оцифровки и анализа. Работы в этом направлении быстро развиваются; более полные обзоры работы других групп в этом направлении можно найти в работах [4, 5, 26].
Интересное развитие работ по анализу изображений — коррекция (улучшение качества) изображений, хотя это можно считать отступлением от предмета характеризации тканей в изложенном выше смысле этого слова. Цель этой процедуры — каким-либо образом преобразовать отображаемые данные так, чтобы облегчить наблюдателю восприятие отдельных признаков. Один из хорошо известных методов этого типа — контрастирование границ. Как известно (гл. 7), глаз легче воспринимает резкую границу, чем размытую, поэтому соответствующая обработка данных позволяет обнаруживать невоспринимаемую размытую границу и представляет ее как резкую.
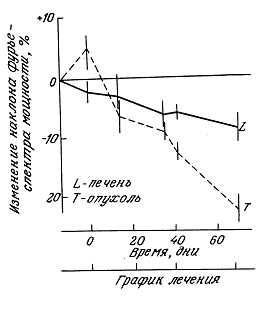
Рис. 10.1. Последовательные изменения одного из параметров текстуры B-изображения (скорость спадания спектра мощности) при обследовании злокачественных узелков (штриховая линия) до и во время химиотерапии. Начальный рост кривой (до химиотерапии) соответствует операции удаления опухоли яичка. Последующая успешная химиотерапия приводит к монотонному уменьшению параметра. Для контроля обследовалась текстура печени (сплошная линия); изменения здесь могут быть обусловлены действием лекарственных веществ, использованных в химиотерапии (неопубликованные данные: Nassiri, Cosgrove).
Другой пример улучшения качества изображения, который оказывается полезным в ряде случаев, — «выравнивание гистограммы амплитуд». Если любую картину разделить на участки изображения с использованием равномерной шкалы уровней амплитуды или яркости, может оказаться, что гистограмма вероятности появления элементов изображения с заданной амплитудой будет содержать весьма резкие пики при одних значениях амплитуды, тогда как другие оказываются относительно маловероятными. Иногда можно улучшить восприятие признаков изображения, если, используя такую гистограмму, модифицировать характеристику отображения так, чтобы уравнять вероятности появления точек заданной амплитуды в любом воспринимаемом элементе изображения.
Рассматривая использование методов повышения качества изображений, важно иметь в виду, что глаз и мозг человека сами обладают замечательной способностью обрабатывать изображения, т. е. могут выделять существенные признаки для достижения конкретной цели, так что искусственная обработка изображения на практике может оказаться малоэффективной.
10.4. ИСПОЛЬЗОВАНИЕ ХАРАКТЕРИСТИК РАССЕЯНИЯ НА ТКАНЯХ
Как уже отмечалось в гл. 6, акустическое рассеяние на тканях может существенно зависеть от некоторых особенностей их структуры, таких как среднее расстояние между эффективными рассеивателями, степень нерегулярности их расположения в пространстве, степень анизотропии, распределение по размерам, формам. Таким образом, могут существовать методы характеризации тканей, в которых измеряются эти параметры и определяются соответствующие свойства рассеяния тканей. Как будет показано, эти методы иногда очень сильно отличаются от изложенных в разд. 10.3, которые также связаны с рассеянием, но используют информацию в виде, определяемом конкретной аппаратурой для получения изображения.
Из общефизических представлений следует ожидать, что некоторые полезные характеристики рассеяния можно получить из измерений его зависимости от частоты акустического сигнала, что подтверждается теоретическими исследованиями, обсуждавшимися в гл. 6. Практическое применение этой идеи обсуждается рядом авторов и хорошо иллюстрируется работами [12, 13], где этот подход использовался для исследования заболеваний глаза и орбиты. Авторы ограничились исследованием тканей на глубине не более 20 мм и с помощью достаточно широкополосного преобразователя могли принимать сигналы в диапазоне 6—14 МГц с хорошим отношением сигнал/шум. Достаточно длинные выборки эхо-сигналов (с достаточно гладкой огибающей, чтобы избежать нежелательной свертки сигнала с этой огибающей) подвергались фурье-преобразованию с помощью аналогового анализатора спектра. Полученный спектр использовался для определения ряда диагностических признаков. Иногда эти признаки могут быть найдены только при усреднении (в частотной области) данных, полученных из множества измерений на соседних участках ткани. Это хороший пример упомянутого выше соотношения неопределенностей между пространственным разрешением и специфичностью характеризации. Во всех случаях спектры нормируются на спектр эхо-сигнала, отраженного от плоской границы раздела вода — стекло.
Некоторые интересные примеры спектров, полученных таким путем, показаны на рис. 10.2.
Отслоившаяся сетчатка, по-видимому, представляется хорошим аналогом «тонкой пластинки» (см. разд. 1.7.4), и этот вывод согласуется с видом спектра, в котором появляются интерференционные минимумы на частотах около 4 и 8 МГц. В предположении, что скорость звука в сетчатке 1500 м/с, такое разнесение частот соответствует толщине сетчатки около 0,19 мм (![]() /2 на 4 МГц). Кроме того, экстраполяция спектра показывает наличие интерференционного минимума на нулевой частоте, что подразумевает разные знаки изменения импеданса на границах раздела (см. разд. 1.7.2).
/2 на 4 МГц). Кроме того, экстраполяция спектра показывает наличие интерференционного минимума на нулевой частоте, что подразумевает разные знаки изменения импеданса на границах раздела (см. разд. 1.7.2).
Этого следует ожидать и для слоя, ограниченного с двух сторон обычной жидкостью. Однако диагностическое значение измерения толщины образца этим способом довольно невелико, и такую информацию проще получить непосредственно по эхограмме исходного сигнала.
Похожий «гребенчатый» спектр показан на рис. 10.2, б, но в этом случае предполагается, что структура спектра связана с локализованной периодичностью или внутренними перегородками в структуре жировой ткани (с разделением по частоте 1,8 МГц, что соответствует 0,42 мм).
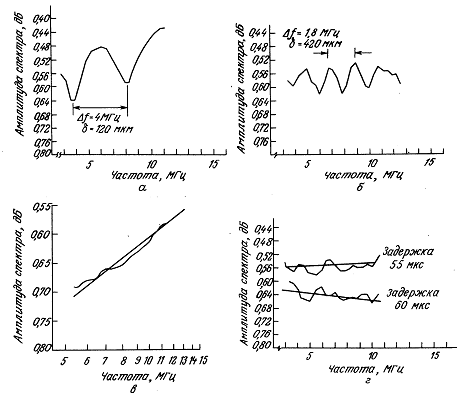
Рис. 10.2. Частотные спектры обратного рассеяния на различных тканях глаза и глазной орбиты [12]: спектры отслоившейся сетчатки (а) и жировой ткани орбиты (б), в которых выраженная регулярность структуры тканей приводит к «гребенчатости», соответствующей характерному размеру структуры 5; спектр сгустка крови в стекловидном теле — неупорядоченной ткани, в которой среднее расстояние между рассеивателями ![]() (рэлеевское рассеяние) (в); спектр злокачественной меланомы — структурированной ткани, для которой, по-видимому,
(рэлеевское рассеяние) (в); спектр злокачественной меланомы — структурированной ткани, для которой, по-видимому, ![]() . Нижняя кривая записана с задержкой 5 мкс относительно верхней, при этом увеличение наклона спектра может служить мерой частотно-зависимого затухания (публикуется с согласия д-ра Лицци).
. Нижняя кривая записана с задержкой 5 мкс относительно верхней, при этом увеличение наклона спектра может служить мерой частотно-зависимого затухания (публикуется с согласия д-ра Лицци).
Другая ситуация представлена на рис. 10.2, в, г, где регулярная гребенчатость спектра не видна, и поэтому, вероятно, слаба структурная регулярность внутри исследуемого объекта. Сгусток крови в стекловидном теле дает спектр, монотонно возрастающий по частоте с наклоном, который соответствует удельному объемному сечению рассеяния, пропорциональному четвертой степени частоты. По-видимому, это соответствует случаю рэлеевского рассеяния, которое вполне можно ожидать для такого материала, как неупорядоченное скопление кровяных телец с размерами порядка длины волны, т. е. не обладающего выраженной рассеивающей структурой на шкале длин волн до 100 мкм (разд. 6.4).
В случае злокачественной меланомы зависимость от частоты слабее, что отвечает структуре, содержащей рассеиватели, размеры и расстояния между которыми сравнимы с длиной волны (разд. 6.4). Однако сравнение наклона спектральных характеристик, взятых при двух различных задержках (т. е. разделенных расстоянием 3,75 мм), показывает, что частотно-зависимое затухание — это, с одной стороны, фактор, который необходимо учитывать, и, с другой — параметр, который таким способом можно оценить количественно (в данном случае - 0,9 дБ/(см • МГц)).
Итак, частотный анализ предоставляет возможность получить несколько показателей, которые можно использовать в качестве дискриминаторов: период изменения частотной характеристики (количественный показатель масштаба регулярной структуры); наклон монотонной частотной характеристики (показатель масштаба тонкой или нерегулярной структуры) и степень зависимости этого наклона от глубины (мера коэффициента затухания).
Использование аналогового анализатора спектра (как в указанной выше работе) — лишь один из ряда близких и в общих чертах эквивалентных подходов к определению информативных признаков для характеризации тканей. В частности, можно численно выполнить фурье-преобразование цифровых данных или, напротив, определить автокорреляционную функцию. Действительно, характеристики «частотного анализа рассеяния» должны быть тесно связаны по крайней мере с несколькими признаками, получаемыми с помощью методов анализа текстуры эхо-импульсного изображения, описанных в предыдущем разделе. Несомненно, должно появиться единое аналитическое описание этих вопросов.
Как уже было кратко отмечено в разд. 6.4.4, возможность получения дополнительной информации о свойствах рассеивающих объектов появляется в том случае, если вместо или в дополнение к исследованию в широком диапазоне частот регистрировать информацию и в широком интервале углов с помощью так называемого «апертурного сканирования». При этом регистрируется обратное рассеяние из по существу постоянного объема ткани в непрерывном интервале углов, в выбранной плоскости сканирования, в одной или нескольких относительно узких частотных областях (рис. 10.3).
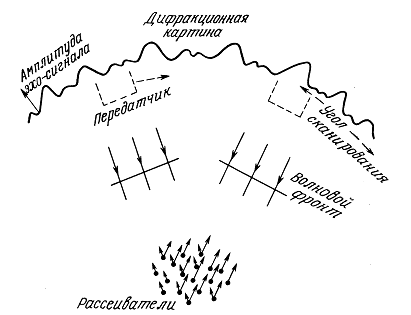
Рис. 10.3. Схематическое изображение дифракционной картины (зависимости амплитуды эхо-сигнала от угла сканирования), полученное при движении преобразователя по дуге относительно одного и того же объема в центре (определенного шириной пучка и стробированием во времени). Эхо-сигналы отдельных рассеивателей интерферируют, складываясь или уничтожая друг друга и порождая для каждого угла сканирования свою результирующую амплитуду эхо-сигнала на приемном преобразователе.
Таким путем можно определить несколько показателей, описывающих результирующую дифракционную картину, а именно (одномерную) зависимость амплитуды эхо-сигнала от угла сканирования.
Эта идея апробировалась в лабораторных экспериментах [18], была проверена в клинике и оказалась пригодной (рис. 10.4) для диагностики болезней печени и щитовидной железы [14, 17]. Однако устройство, в котором она первоначально была использована и опробована [6], было громоздким и непосредственно не стыковалось со стандартной аппаратурой для визуализации, так что оценки практических возможностей этого метода не были сделаны. Это стало возможно лишь тогда, когда появились решетки преобразователей и методики обработки, позволяющие применять апертурное сканирование как дополнительный режим работы сканера с широкой апертурой и фазированной решеткой [21]. Такая система дает возможность вести одновременное исследование в трех связанных режимах (анализ текстуры, частотного спектра и ориентационный анализ).
Рис. 10.4. Одномерные дифракционные картины, полученные на частоте 2,5 МГц от нормальной печени (а, б) и при циррозе {в, г) [17].
Мощное развитие этот принцип может получить при использовании двумерной апертуры вместо одномерной. По аналогии с рентгеновской кристаллографией одномерный вариант — это брэгговский метод, а двумерный — метод Лауэ. Пример показан на рис. 10.5, а соответствующая двумерная диаграмма признаков — на рис. 10.6 (ср. разд. 7.5).
Развитие двумерной апертурной обработки в перспективе может дать два преимущества. Во-первых, число независимых выборок информации, которое можно получить из заданного объема ткани, при этом сильно возрастает. Следовательно, можно ожидать, что это улучшит специфичность характеризации, поскольку увеличивается отношение сигнал/шум. Во-вторых, использование двумерной апертуры позволяет исследовать заданный объем в трех измерениях, что в принципе дает возможность однозначно восстановить исходную рассеивающую структуру. Здесь снова очевидна аналогия с кристаллографией.
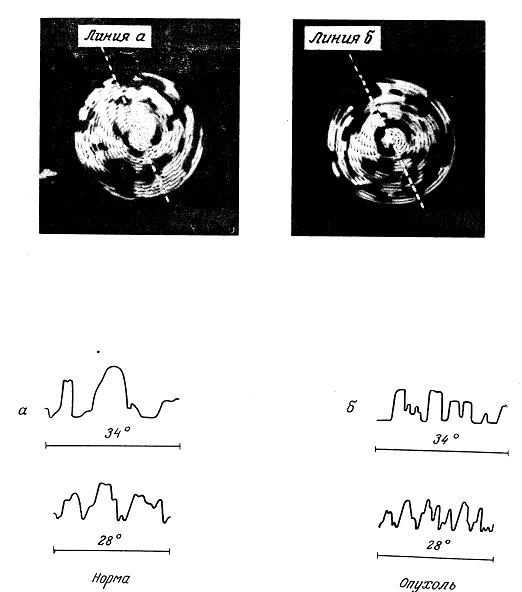
Рис. 10.5. Двумерные дифракционные картины (вверху) от нормальной печени (а) и вторичной опухоли печени (б). Под ними помещены соответствующие им одномерные картины, построенные по указанным на фотографиях линиям. Внизу для сравнения показаны дифракционные картины от подобных же тканей, полученные с помощью того же преобразователя на той же частоте одномерным методом [22].
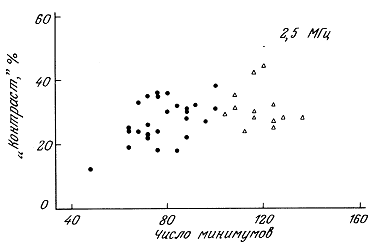
Рис. 10.6. Карта разброса для двух признаков, характеризующих двумерную дифракционную картину, показанную на рис. 10.5 (частота 2,5 МГц). Очевидно, в данном случае число минимумов дифракционной картины, приходящихся на 1 ср угла сканирования, более пригодно в качестве дискриминатора, чем «контраст» (мера отношения минимальной и максимальной амплитуд эхо-сигналов) [22].
Некоторые модификации такой методики весьма широко обсуждались под названием дифракционной томографии (гл. 6, 9).
10.5. ИСПОЛЬЗОВАНИЕ ПАРАМЕТРОВ ДВИЖЕНИЯ ТКАНЕЙ
Как уже отмечалось, ультразвук обладает уникальными возможностями для регистрации динамических процессов в организме. Это прекрасно иллюстрируется некоторыми результатами ультразвуковой визуализации (звуковидения в реальном времени): дополнительность визуализации и телегистологии касается и временных измерений.
Движения биологических тканей можно разделить на четыре типа: первичное (например, движение сердца или плода в организме матери), вторичное (например, движение ткани печени под действием пульсаций близлежащего магистрального кровеносного сосуда), течение жидкости (в частности, кровоток) и движения, обусловленные внешними причинами. Очевидно, наиболее важными являются первичные движения и потоки. Интерес к вторичным и вынужденным движениям обусловлен тем, что они могут нести информацию об объемных механических свойствах тканей (т. е. об объемном и, возможно, сдвиговом модулях упругости). Эти свойства тканей уже давно оцениваются в клинической диагностике путем пальпации.
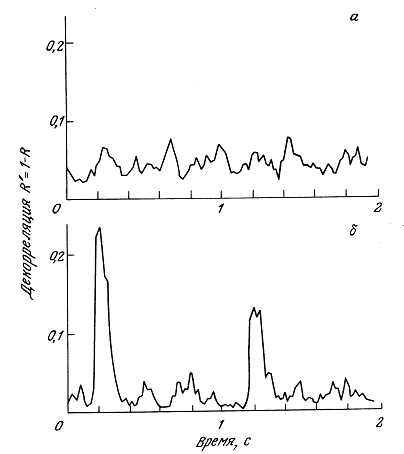
Рис. 10.7. Изменение с течением времени декорреляции А-эхограмм нормальной ткани печени (а) и вторичной опухоли печени пациента с карциномой прямой кишки (б). Декорреляция определяется как 1 - R, где R — коэффициент корреляции между А-эхограммами, записанными с интервалом в 0,1 кардиоцикла. Каждая кривая длится два кардиоцикла (неопубликованные данные: Tristam).
Использование обследования в режимах ТМ или М для записи сокращений сердца уже описано в гл. 8 и не требует здесь дальнейшего обсуждения; отметим лишь, что логически этот режим можно считать разновидностью телегистологии. Сходную методику можно использовать для «дистанционной пальпации» — исследования отклика тканей на вынужденное движение. Например, в работе [2] эта техника, основанная на измерении сжимаемости, использована
для нахождения глубоко залегающих опухолевых участков в молочной железе.
Полученный опыт показал, что эта методика полезна, но на ее точности неблагоприятно сказывается когерентность излучения, в особенности если отсутствуют четкие макроскопические границы раздела. В этом случае более строгий подход к характеризации движения состоит в определении изменений во времени декорреляции между последовательными А-эхограммами, зарегистрированными в одном направлении в исследуемом объеме ткани [3]. Предварительные оценки, представленные на рис. 10.7, показывают, что этот параметр может служить дискриминатором для различения жестких и эластичных тканей при вынужденном или вторичном движении [24].
Доплеровские измерения кровотока подробно рассмотрены в гл. И. Зачастую цель такого обследования — определение локальных характеристик выбранного кровеносного сосуда (например, закупорки, склерозирования стенки). Этот метод также можно считать разновидностью телегистологии; использование этого термина особенно уместно в ситуации «ангиогенеза опухоли», когда на развитие кровеносных сосудов и кровотока сильно влияют опухолевые или циррозные изменения окружающих слоев ткани. Это служит основой для применения доплеровской характеризации кровотока при исследовании роста опухолей молочной железы и их реакции на лечение [15].
Ультразвуковая телегистология или «характеризация тканей» — новое, развивающееся, но еще не проверенное всесторонне научное направление. Методы и подходы телегистологии тесно связаны с методами получения изображений, но, вообще говоря, являются дополнительными. Истинно системный подход к этому предмету еще только намечается, и, очевидно, будет тесно связан с пониманием физики взаимодействия ультразвука с тканями.
1. Chivers, R. С. (1981) Tissue characterization. Ultrasound Med. Biol. 7, 1—20.
2. Dale, G. & Gros, C. (1981) Diagnostician's requirements for ultrasonic imaging of the breast: a critical assessment, in: Medical ultrasonic images: formation, display, recording and perception (ed. C. R. Hill & A. Kratochwil) pp. 126—133, Amsterdam, Excerpta Medica.
3. Dickinson, R. J. & Hill, C. R. (1982) Measurement of soft tissue motion using correlation between A-scans. Ultrasound Med. Biol. 8, 263—271.
4. Hill, C. R. (1980) Tissue characterization, in: Progress in medical ultrasound, Vol. 1. (ed. A. Kurjak) pp. 11—18, Amsterdam, Excerpta Medica.
5. Hill, C. R. (1981) Tissue characterization, in: Progress in medical ultrasound, Vol. 2. (ed. A. Kurjak) pp. 19—25, Amsterdam, Excerpta Medica.
6. Huggins, R. W. & Phelps, J. V. (1976) An ultrasonic scanner for recording the angular dependence of echoes from a fixed tissue volume in vivo. Ultrasound in Med. and Biol. 2, 271—277.
7. Lersky, R. A., Morley, P., Barnett, E., Mills, P. R., Watkinson, G., & MacSween, R. N. M. (1982) Ultrasonic characterization of diffuse liver disease: the relative importance of frequency content in the ultrasonic signal. Ultrasound Med. Biol. 8, 155—160.
8. Lersky, R. A., Smith, M. J., Morley, P., Barnett, E., Mills, P. R., Watkinson, G., & MacSween, R. N. M. (1981a) Discriminant analysis of ultrasonic texture data in diffuse alcoholic liver disease, I: fatty liver cirrhosis. Ultrasonic imaging 3, 164—172.
9. Lersky, R. A., Morley, P., Mills, P. R., & Watkinson, G. (1981b) Texture analysis of ultrasonic signals: a comparison of the use of radiofrequency and demodulated A-scan data. Ultrasonic Imaging 3, 369—377.
10. Linzer, M. (1976) Ultrasonic tissue characterization: NBS Special Publication 453. Washington D. C, U S. Govt. Printing Office.
11. Linzer, M. (1979) Ultrasonic tissue characterization II: NBS Special Publication 525. Washington D. C, U. S. Govt. Printing Office.
12. Lizzi, F. L. & Coleman, D. J. (1977) Ultrasonic spectrum analysis in ophthalmology, in: Recent advances in ultrasound in biomedicine. Vol. 1. (ed. D. N. White) pp. 117—130, Forest Grove, Research Studies Press.
13. Lizzi, F. L., Laviola, M. A., & Coleman, D. J. (1976) Tissue signature characterization using frequency domain analysis, in: 1976 IEEE Ultrasonic Symposium Proceedings, pp. 714—719, IEEE (Cat. No. 76 CH1120—5SU).
14. Merton, J., Nicholas, D., Hill, C. R., Grover, S., Queenan, M., & Cosgrove, D. (1982) Ultrasonic diffraction scanning of the thyroid. Ultrasound in Med. and Bio!. 8, 145—153.
15. Minassian, H., & Bamber, J. C. (1982) A preliminary assessment of an ultrasonic Doppler method for the study of blood flow in human breast cancer. Ultrasound Med. Biol. 8, 257—264.
16. Mountford, R. A., & Wells, P N. T. (1972) Ultrasonic liver scanning: the A-scan in normal and cirrhosis. Phys. Med. Biol. 17, 261—269.
17. Nicholas, D. (1979) Ultrasonic diffraction analysis in the investigation of liver disease. Brit. J. Radiol. 52, 949—961.
18. Nicholas, D., & Hill, C. R. (1975) Acoustic Bragg diffraction from human tissues. Nature 257, 305—306.
19. Nicholas, D., Nassiri, D. K., Bamber, M., Bossi, C, Garbutt, P., Hinton, J., & Pussell, S. (1982a) Classification of diffuse liver disorders by quantitative evaluation of B-mode echograms. Ultrasound in Med. and Biol. 8, (Suppl. 1), 140.
20. Nicholas, D., Nassiri, D. K., Bossi, C, Cosgrove, D. O., Garbutt, P., & Pussell, S. (1982b) Quantitative analysis of abdominal neoplasms. Ultrasound in Med. and Biol. 8, (Suppl. 1) 141.
21. Nicholas, D., Bossi, C, & Pussell, S. (1982c) 'Real-time' in vivo diffraction scanning. Ultrasound in Med. and Biol. 8, (Suppl. 1) 141.
22. Nicholas, D., & Nicholas, A. W. (1983) Two-dimensional diffraction scanning of normal and cancerous human hepatic tissue in vitro. Ultrasound in Med and Biol. 9, 283—295.
23. Nicholas, D., Nassiri, D. K., Garbutt, P., & Hill, C. R. (1986) Tissue characterization from ultrasound B-scan data. Ultrasound in Med. and Biol. 12, 135—143.
24. Tristam, M., Barbosa, D. C., Cosgrove, D. O., Nassiri, D. K., Bamber J. C, & Hill, C. R. (1986/7) Ultrasound in Med. and Biol, (in press).
25. Thijssen J. M. (1980) Ultrasonic tissue characterization: clinical achievements and technological potentials. Brussels, Stafleu.
26. Thijssen, J. M. (1982) Ultrasonic tissue differentiation, in Progress in medical ultrasound, Vol. 3, pp. 23—36 (A. Kurjak, ed.) Amsterdam, Excerpta Medica.
ДОПЛЕРОВСКИЕ МЕТОДЫ
П. Фиш
Частота ультразвука, принятого от движущегося отражателя (или рассеивателя), отличается от частоты излученного сигнала. Это явление называют эффектом Доплера, а величину изменения частоты, пропорциональную скорости движения отражателя (или рассеивателя), — доплеровским сдвигом. Смешивая излученной и принятый сигналы, получают разностный (доплеровский) сигнал, частота которого равна доплеровскому сдвигу. Для связанных с движением многих физиологических процессов в организме величина этого сдвига находится в диапазоне звуковых частот, что и привело к созданию простых индикаторов скорости, в которых доплеровский сигнал подается на наушники или громкоговорители. Оператор, работающий с таким прибором, может на слух определить наличие перемещения какого-либо отражателя (или рассеивателя) на пути ультразвукового пучка, а при некотором опыте — судить о характере движения. Такие устройства были использованы для определения внутриутробного сердцебиения плода [10, 34] и вибраций стенок сосудов при измерении артериального давления [43]. В обоих случаях эти приборы использовались как своеобразный стетоскоп; при этом регистрировались мощные ультразвуковые сигналы от отражающих структур. Однако наибольший интерес вызывает задача регистрации и измерения параметров кровотока [4], когда ультразвук рассеивается на форменных элементах крови, хотя для работы со слабыми рассеянными сигналами требуется более сложная аппаратура. Оператор может определить, доступен ли сосуд, находящийся на пути пучка, доплеровскому обследованию, а при наличии опыта может обнаружить высокие доплеровские частоты от ускоренного кровотока в сужении сосуда, а также турбулентность за сужением.
Диагностические возможности ультразвукового измерителя скорости кровотока можно расширить в нескольких направлениях. Его можно применять для визуализации кровотока в сосудах [42], прикрепив ультразвуковой зонд к координатному устройству, которое позволяет синхронно с зондом перемещать на запоминающем мониторе яркостную отметку. При появлении доплеровского сигнала отметка усиливается и запоминается, причем при стенозе изображение сосуда будет суженным. Если доплеровский сигнал подать на частотный детектор, а с него на регистратор или осциллограф, можно зарегистрировать кривую скорости артериального кровотока. Вид этой кривой зависит от состояния артериального русла и может использоваться для диагностики заболеваний сосудов [22, 26, 40]. Подавая доплеровский сигнал на анализатор спектра, можно получить распределение доплеровских частот, обусловленное тем, что элементы крови движутся внутри сосуда с различными скоростями [6]. Такой способ отображения особенно ценен для обнаружения турбулентности, так как его чувствительность, возможно, выше, чем при прослушивании сигналов малоквалифицированным оператором.
Простейший доплеровский прибор излучает непрерывный смодулированный ультразвук и называется доплеровским прибором непрерывного излучения (ДПНИ). Так как он реагирует на кровоток в любой области пучка (хотя чувствительность и падает с глубиной из-за затухания сигнала), его нельзя использовать для различения сосудов, находящихся на разных глубинах, или для измерения профиля скоростей в одном сосуде. Для решения этих задач необходима информация о глубине, которую получают путем модуляции излучаемого сигнала. Определенное состояние модулированного сигнала жестко связано с моментом излучения, и, выделяя это состояние в рассеянном сигнале, можно определить время его запаздывания и тем самым определить глубину рассеивателя. Обычно используется амплитудная модуляция последовательностью импульсов — такие приборы называют импульсно-доплеровскими локаторами [5, 31].
Комбинация В-сканера реального времени и импульсно-доплеровского устройства, называемая дуплексным сканером, обычно используется для одновременной визуализации сосуда и регистрации кровотока [7].
Доплеровские приборы, обладающие разрешением по глубине, могут применяться в устройствах визуализации, которые позволяют формировать изображения, требующие знания о глубине [16, 28]. Они могут использоваться не только для селекции сосудов, залегающих на разных глубинах, но и для построения профиля скоростей, распределения скорости кровотока в поперечном сечении сосуда [32].
Когда требуется измерение абсолютного значения скорости (а не кривая скорости и не профиль кровотока), возникает следующая проблема. Измеренный доплеровский сдвиг частоты пропорционален не только скорости кровотока, но также и углу между вектором скорости и ультразвуковым пучком, так что знание этого угла необходимо, чтобы вычислить скорость по доплеровскому сдвигу. Для решения этой задачи разработан ряд методов [17]. При этом необходимо каким-либо вспомогательным способом измерять угол или ориентировать ультразвуковые пучки под определенным углом; в любом случае для измерения абсолютной скорости необходимо осуществлять тригонометрические преобразования (триангуляцию).
Следующая проблема после измерения абсолютной скорости кровотока — вычисление объемного расхода потока крови. Оно заключается либо в измерении средней по пространству (по сечению сосуда) скорости при равномерном облучении сосуда и независимом измерении площади его сечения [15, 20], либо в интегрировании измеренного профиля скоростей [8, 18].
Около 20 лет понадобилось, чтобы от первых доплеровских приборов непрерывного излучения перейти к первым серийным измерителям объемного расхода крови. Большая часть разработок была эмпирической, и мы до сих пор еще далеки как от полного понимания процессов формирования доплеровских сигналов, так и от разработки оптимизированных доплеровских систем для решения частных клинических задач. Парадоксально, но некоторые физиологические характеристики, такие, как профиль скоростей, необходимые для оптимизации системы и понимания особенностей формирования доплеровских сигналов, могут быть измерены только с помощью самих доплеровских методов.
Эффект Доплера — зависимость наблюдаемой частоты периодического колебания от любого изменения расстояния между источником колебаний и наблюдателем. Этот эффект появляется, если наблюдатель или источник (или они оба) движутся или если излучение от неподвижного источника к неподвижному наблюдателю приходит, отражаясь или рассеиваясь от движущегося объекта.
Если источник и наблюдатель движутся вдоль одной прямой со скоростями соответственно Vs и Vr, то наблюдаемая частота определяется выражением [44]
![]()
где fs — частота колебаний источника, с — скорость распространения излучения. Отсюда получаем выражение для доплеровского смещения:
В ультразвуковой доплеровской локации обычно имеются неподвижный источник (излучатель), неподвижный наблюдатель (приемный преобразователь) и движущийся отражатель (или рассеиватель) ультразвука.
При измерении скорости кровотока ультразвук рассеивается на флуктуациях плотности и сжимаемости, и принятый сигнал можно вычислить как сумму сигналов от всех элементов крови на пути ультразвукового пучка. На рис. 11.1 показан случай одного рассеивателя, движущегося со скоростью V. Доплеровский сдвиг от движущегося отражателя (или рассеивателя) можно вычислить, рассматривая его в системе наблюдателя, движущегося относительно источника (излучателя), а затем в системе источника, движущейся относительно наблюдателя (приемника). Кроме того, поскольку направления распространения падающей и рассеянной волн не совпадают с направлением движения элемента крови, уравнение (11.2) нельзя использовать непосредственно — необходимо заменить Vs и Vr составляющими этих скоростей вдоль направлений приема и излучения. Получаем следующее:
где ![]() и
и ![]() — углы между вектором скорости и направлениями излучения и приема; f0 — частота излучения.
— углы между вектором скорости и направлениями излучения и приема; f0 — частота излучения.
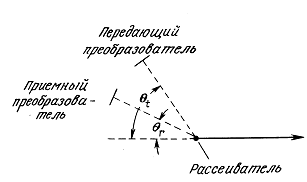
Рис. 11.1. Конфигурация, в которой при движении рассеивателя относительно неподвижных излучателя (передающего преобразователя) и наблюдателя (приемного преобразователя) возникает доплеровский сдвиг частоты.
Поскольку с ~ 1500 м/с, а ![]() , справедливо приближение
, справедливо приближение
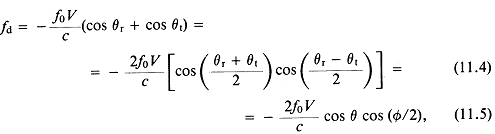
где ![]() есть угол между вектором скорости и биссектрисой угла между направлениями излучения и приема,
есть угол между вектором скорости и биссектрисой угла между направлениями излучения и приема, ![]() — угол между самими этими направлениями. Обычно в зонде (датчике) совмещаются передающий и приемный преобразователи, как это показано на рис. 11.2. При этом биссектриса угла
— угол между самими этими направлениями. Обычно в зонде (датчике) совмещаются передающий и приемный преобразователи, как это показано на рис. 11.2. При этом биссектриса угла ![]() совпадает с осью «измерительного объема», т. е. области перекрытия двух пучков. Зачастую
совпадает с осью «измерительного объема», т. е. области перекрытия двух пучков. Зачастую ![]() — достаточно малый угол, так что приближенно
— достаточно малый угол, так что приближенно ![]() , и поэтому из (11.5) получаем
, и поэтому из (11.5) получаем
![]()
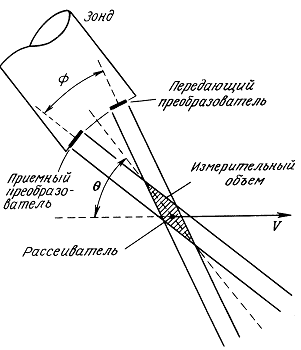
Рис. 11.2. Зонд, передающий и приемный преобразователи и пучки доплеровского прибора непрерывного излучения, ![]() — Угол между падающим и отраженным пучками,
— Угол между падающим и отраженным пучками, ![]() — угол между биссектрисой угла между пучками и вектором скорости.
— угол между биссектрисой угла между пучками и вектором скорости.
Выражения (11.5) и (11.6) показывают, что:
1) частота доплеровского сдвига ![]() пропорциональна частоте излучения. Увеличение затухания и возрастание мощности рассеянного сигнала с ростом частоты и ширины пучка делает оптимальным выбор диапазона f0 2-20 МГц. При этом частоты доплеровского сдвига находятся в звуковом диапазоне;
пропорциональна частоте излучения. Увеличение затухания и возрастание мощности рассеянного сигнала с ростом частоты и ширины пучка делает оптимальным выбор диапазона f0 2-20 МГц. При этом частоты доплеровского сдвига находятся в звуковом диапазоне;
2) ![]() пропорциональна скорости движения отражателя (рассеивателя);
пропорциональна скорости движения отражателя (рассеивателя);
3) ![]() обратно пропорциональна скорости ультразвука в биологической ткани;
обратно пропорциональна скорости ультразвука в биологической ткани;
4) ![]() зависит от углов, образуемых вектором скорости с направлениями излучения и приема; в частности, при
зависит от углов, образуемых вектором скорости с направлениями излучения и приема; в частности, при ![]() .
.
11.3. ДОПЛЕРОВСКИЙ ПРИБОР НЕПРЕРЫВНОГО ИЗЛУЧЕНИЯ
Блок-схема простейшего ультразвукового ДПНИ, предложенного Сатомурой [35] в 1957 г., представлена на рис. 11.3. Передающий преобразователь (излучатель) соединен с генератором, работающим в диапазоне 2—20 МГц, и непрерывно излучает ультразвуковой пучок. Ультразвук рассеивается и отражается, а затем улавливается приемным преобразователем, усиливается и перемножается с сигналом генератора.
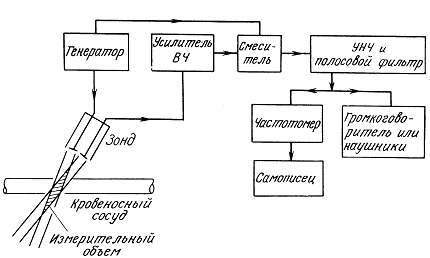
Рис. 11.3. Доплеровский прибор непрерывного излучения.
Запишем излученный сигнал в виде
![]()
а сигнал, принятый от единичного рассеивателя, с точностью до постоянного множителя в виде
![]()
где ![]() — величина фазы, зависящая от расстояния до рассеивателя и фазового сдвига в приемном тракте. Тогда сигнал на выходе перемножителя будет иметь вид
— величина фазы, зависящая от расстояния до рассеивателя и фазового сдвига в приемном тракте. Тогда сигнал на выходе перемножителя будет иметь вид
![]()
Второй член этого выражения имеет удвоенную .частоту и отфильтровывается в усилителе низких частот, следующем за перемножителем. Остается лишь доплеровский сигнал, т. е. сигнал с частотой доплеровского сдвига: .
![]()
После усиления и фильтрации в соответствующей полосе частот доплеровский сигнал поступает на наушники, громкоговоритель или на частотомер.
Ультразвуковой сигнал, воспринимаемый приемным преобразователем, содержит не только сигналы, рассеянные на форменных элементах крови, но и сигналы гораздо большей амплитуды, отраженные от других структур, таких как границы жировой и мышечной ткани или стенки сосудов. Такие сигналы обычно на 40—50 дБ превышают сигналы от кровотока, и это соотношение может быть еще большим при локации глубоко залегающих сосудов. Кроме того, эти мощные сигналы сами могут обладать низкочастотным доплеровским сдвигом, вызванным движением окружающих структур (например, движением пульсирующих артерий) или случайными смещениями зонда в руке оператора относительно неподвижных отражателей. Чтобы подавить эти мощные низкочастотные доплеровские сигналы, в НЧ-усилитель вводят фильтры верхних частот. Фильтрация необходима на входе усилителя или после небольшого предусиления, иначе сигналы будут смешиваться в усилителе. Неизбежный побочный эффект такой фильтрации — потеря низкочастотных доплеровских сигналов от медленного кровотока.
Чтобы ограничить ширину полосы НЧ-усилителя и тем самым свести к минимуму мощность флуктуационного шума, в усилитель вводят НЧ-фильтры, верхняя частота среза которых устанавливается равной максимальной ожидаемой доплеровской частоте, поскольку излишнее увеличение частоты среза может привести лишь к росту уровня шума.
Так как внутри измерительного объема существует распределение скоростей кровотока в поперечном сечении сосуда, т. е. рассеиватели могут двигаться с разными скоростями, доплеровский сигнал представляет собой суперпозицию доплеровских сигналов, частота каждого из которых соответствует скорости конкретного рассеивателя. Суммарный доплеровский сигнал при этом имеет сплошной спектр, а частотомер будет показывать лишь среднюю из этих частот. Если угол ![]() известен, то, используя уравнение (11.5) или (11.6), можно преобразовать измеренную среднюю частоту в скорость. Эта скорость есть средневзвешенное по линиям тока, проходящим через измерительный объем. Вклад каждой линии тока в среднюю скорость пропорционален мощности ультразвука, рассеянной элементами крови вдоль данной линии, т. е. интегралу по линии тока от чувствительности в пучке (зависимости величины сигнала, принятого от точечного рассеивателя, от координат этого рассеивателя). Более строго это будет показано в разд. 11.5.1.
известен, то, используя уравнение (11.5) или (11.6), можно преобразовать измеренную среднюю частоту в скорость. Эта скорость есть средневзвешенное по линиям тока, проходящим через измерительный объем. Вклад каждой линии тока в среднюю скорость пропорционален мощности ультразвука, рассеянной элементами крови вдоль данной линии, т. е. интегралу по линии тока от чувствительности в пучке (зависимости величины сигнала, принятого от точечного рассеивателя, от координат этого рассеивателя). Более строго это будет показано в разд. 11.5.1.
Если этот интеграл не изменяется по сечению сосуда, то измеренная скорость — средняя по пространству скорость кровотока. Условие постоянства интеграла часто называют условием равномерности облучения, что подразумевает постоянство интенсивности излучения по сечению сосуда, хотя в действительности это условие является более строгим.
Описанный выше прибор не позволяет выделять направление кровотока. Из выражений (11.5) и (11.6) следует, что доплеровское смещение положительно, если составляющая вектора скорости направлена к зонду, и отрицательно, если от зонда. Однако этот простейший прибор не сохраняет информацию о направлении кровотока, а дает лишь величину сдвига частоты. Информация о направлении необходима, чтобы следить за изменением скорости кровотока в течение кардиоцикла в тех сосудах, где возникает обратный кровоток, или если направление кровотока несет диагностическую информацию, например при исследовании вен при недостаточности сердечных клапанов.
Информацию о направлении можно сохранить различными способами [12, 13, 14]. Соответствующие устройства представлены на рис. 11.4. В первом из них (рис. 11.4, а) принятый высокочастотный сигнал пропускается через два фильтра, один из которых отсекает частоты ниже частоты излучения и пропускает сигналы с положительным доплеровским сдвигом вплоть до максимальной угловой частоты ![]() , а другой пропускает сигналы с отрицательным доплеровским сдвигом. Как и ранее, сигналы с выхода каждого из фильтров поступают на перемножители и НЧ-усилители.
, а другой пропускает сигналы с отрицательным доплеровским сдвигом. Как и ранее, сигналы с выхода каждого из фильтров поступают на перемножители и НЧ-усилители.
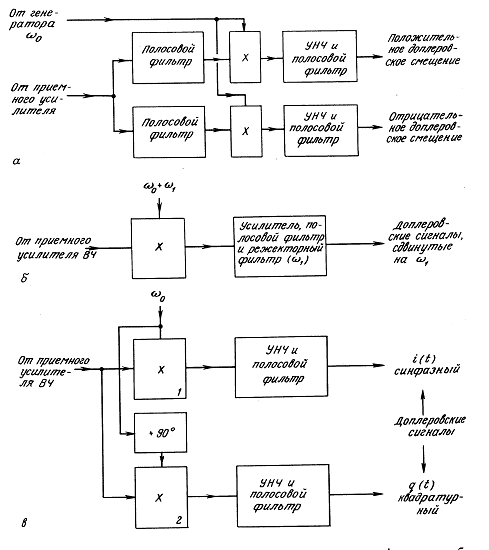
Рис. 11.4. Методы выделения информации о направлении потока: фильтрация боковых полос (а); демодуляция со сдвигом несущей частоты (б); квадратурная демодуляция сигналов (в).
В устройстве, показанном на рис. 11.4,6, принятый сигнал перемножается с опорным сигналом, смещенным на ![]() относительно частоты излучения. Спектр доплеровских сигналов при этом оказывается смещенным относительно истинного на величину
относительно частоты излучения. Спектр доплеровских сигналов при этом оказывается смещенным относительно истинного на величину ![]() при этом сдвиг
при этом сдвиг ![]() выглядит как
выглядит как ![]() , а сдвиг
, а сдвиг ![]() как
как ![]() . Направление кровотока определяется взаимным расположением доплеровского сдвига и частоты смещения an. Очевидно, частота an должна быть выбрана выше наибольшего отрицательного доплеровского сдвига, а фильтр, отсекающий мощные паразитные сигналы, преобразуется здесь в полосовой режекторный фильтр с центральной частотой ал.
. Направление кровотока определяется взаимным расположением доплеровского сдвига и частоты смещения an. Очевидно, частота an должна быть выбрана выше наибольшего отрицательного доплеровского сдвига, а фильтр, отсекающий мощные паразитные сигналы, преобразуется здесь в полосовой режекторный фильтр с центральной частотой ал.
Третья возможность построения прибора представлена на рис. 11.4, е. В этом случае принятый сигнал поступает на два перемножителя, на одном из которых опорный сигнал сдвинут на 90° относительно другого. Для первого перемножителя опорный сигнал можно представить в виде ![]() , для второго — в виде
, для второго — в виде ![]() . При этом синфазный сигнал i(t) аналогичен (11.9):
. При этом синфазный сигнал i(t) аналогичен (11.9):
![]()
а квадратурный сигнал описывается выражением
![]()
Знак доплеровского сдвига, а значит, и направление кровотока определяется по соотношению фаз i(t) и q(t). Если сдвиг cod положителен, то квадратурный сигнал отстает на 90° от синфазного, а если сдвиг ом отрицателен, то опережает его.
11.4. ИМПУЛЬСНО-ДОПЛЕРОВСКИЙ ИЗМЕРИТЕЛЬ СКОРОСТИ КРОВОТОКА
Наиболее существенное ограничение ДПНИ — отсутствие пространственного разрешения, т. е. возможности разделить доплеров-ские сигналы из различных точек в пределах пучка. Если на пути пучка находятся два сосуда, то доплеровский сигнал представляет собой смесь сигналов от обоих сосудов. Невозможно также разделить и скорости в различных точках одного сосуда, т. е. измерять профиль скоростей.
Для решения этой задачи был создан импульсный измеритель скорости кровотока [5, 31], блок-схема которого представлена на
Рис. 11.5. Одноканальный импульсно-доплеровский прибор.
рис. 11.5. Пространственное разрешение достигается благодаря периодическому излучению короткого (несколько колебаний) импульса ультразвука (частота повторения импульсов задается синхронизатором, а канал излучения открывается на время импульса) и использованию смесителя, в котором опорным сигналом служит задержанный во времени излученный сигнал (или эквивалентная «выборка» из принятого сигнала). Так как излучение и прием разнесены во времени, в зонде можно использовать один преобразователь. Такое устройство чувствительно к кровотоку лишь внутри некоторой области в пучке (в измерительном объеме). При этом время распространения излученного импульса до этого объема и обратно равно задержке между выборками излученного и принимаемого сигналов.
Таким образом, простым изменением задержки измерительный объем можно перемещать вдоль оси пучка и использовать это для раздельного наблюдения кровотока на различных глубинах или в различных точках по сечению сосуда. Ширина измерительного объема определяется шириной пучка, а длина — длительностью излучаемого импульса, длительностью опорного импульса и временными характеристиками схемы смесителя. Следует отметить, что понятие «измерительный объем» довольно расплывчато. Поперек пучка и вдоль его оси чувствительность меняется постепенно, поэтому нельзя установить четкие границы измерительного объема, вне которого прибор полностью нечувствителен к кровотоку, а внутри чувствительность постоянна. Границы измерительного объема, показанные на рисунках, больше соответствуют линиям равной чувствительности. Для описания зависимости мощности сигнала точечного рассеивателя от его положения в измерительном объеме будем использовать понятие «функция чувствительности измерительного объема», а более простым понятием «измерительный объем» будем пользоваться там, где распределение чувствительности несущественно для понимания материала.
Средняя частота, измеренная импульсно-доплеровским прибором } _ это среднее взвешенное значение по скоростям на линиях тока, проходящих через измерительный объем. Вклад от линии тока, как и для ДПНИ, пропорционален интегралу от функции чувствительности измерительного объема вдоль линии тока.
Как будет показано ниже, стробированный и демодулированный принятый сигнал кроме собственно доплеровского сигнала содержит также и его гармоники, сдвинутые по частоте на частоту следования импульсов. Эти паразитные сигналы убираются фильтром нижних частот.
Описанный выше прибор — одноканальный, т. е. с одним измерительным объемом. Профиль скоростей в таком приборе измеряют, последовательно перемещая измерительный объем вдоль оси пучка и поперек кровеносного сосуда. Чтобы ускорить процесс съема информации, можно разработать прибор с несколькими одновременно выставляемыми измерительными объемами; каждый из них будет иметь свою задержку опорного сигнала, смеситель и НЧ-усилитель, причем положение измерительных объемов будет определяться задержкой.
Определение направления кровотока чаще всего достигается путем применения синфазного и квадратурного опорных сигналов (см. разд. 11.3 —случай ДПНИ).
11.5. АНАЛИЗ СПЕКТРА ДОПЛЕРОВСКОГО СИГНАЛА
Как уже отмечалось, в доплеровский сигнал вносят вклад все проходящие через пучок линии тока в исследуемом сосуде. Однако спектр частот доплеровского сигнала определяется не только скоростями на этих линиях тока, но и характеристиками падающего и отраженного пучков. Чтобы оценить степень этого влияния, необходимо в общем виде определить вид доплеровского спектра.
Первые расчеты исходили из предположения о независимом рассеянии ультразвука на отдельных форменных элементах крови [9, 19]. Однако, как известно (гл. 6), среднее расстояние между эритроцитами довольно мало (объемная концентрация в норме — 45%) и, как показано в работе [37], обратное рассеяние от них при такой концентрации составляет около 7% от расчетной величины для независимых элементов. Приближение независимых рассеивателей было развито в работе [3], где взаимодействие между ними было учтено тем, что каждый эритроцит исключает остальные из занимаемого им пространства. Однако эта теория также расходится с экспериментом. Трудности можно преодолеть, если учесть, что на длине волны ультразвука укладывается очень много эритроцитов, и кровь рассматривать как сплошную среду, в которой происходит рассеяние на флуктуациях плотности и сжимаемости [21], вызванных случайными изменениями концентрации (и, возможно, ориентации) эритроцитов. Анализ рассеяния ультразвука на движущейся крови как сплошной среде выполнен в работе [2]. В дальнейшем при исследовании доплеровского спектра нами будет использован и развит этот метод. Вычисления будут выполняться в комплексной форме. На практике действительную и мнимую (синфазную и квадратурную) составляющие доплеровского сигнала, как было показано ранее, можно получить с помощью двух демодуляторов с синусоидальным и косинусоидальными опорными сигналами.
Рассеянная из области R волна звукового давления (рассеиватели — эритроциты) для случая монохроматической падающей волны записывается в виде [27]
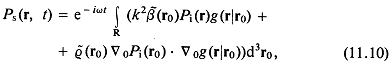
где
![]()
есть падающая на область R волна,
![]() |
|
k — волновое число, ![]() и
и ![]() определены в гл. 6.
определены в гл. 6.
Первый член подынтегрального выражения (11.10) имеет вид волны давления от монополя, а второй — от диполя [27]. Следовательно, приемный преобразователь «видит» монопольное и дипольное излучение из области R. Рассмотрим теперь влияние этих двух волн давления на электрический сигнал приемного преобразователя.
Монополь производительностью S — это изотропный излучатель и может рассматриваться как сфера пренебрежимо малого радиуса ![]() , так что радиальная скорость по его поверхности есть
, так что радиальная скорость по его поверхности есть

а давление в точке r от монополя с координатами r0 равно
![]()
Следовательно, при плотности распределения монополей ![]() в области R получаем волну давления
в области R получаем волну давления
![]()
Волна давления от диполя производительностью D будет
![]()
и для плотност распределения диполей ![]() в области R имеем
в области R имеем
![]()
Диполь можно рассматривать как два монополя производительностью S и –S; вектор d направлен от отрицательного монополя к положительному .
Это можно показать, рассматривая сумму давлений от двух таких монополей:
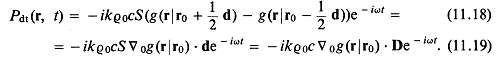
Определим характеристику чувствительности приемного преобразователя Аr(r0) как чувствительность к излучению монополя единичной производительности.
Напряжение на выходе преобразователя (отклик на излучение монополя производительностью S, находящегося в точке r0):
![]()
Тогда отклик приемного преобразователя на распределение монополей с плотностью ![]() в области R представляется в виде
в области R представляется в виде
![]()
Отклик на распределение диполей с плотностью ![]()
![]() получаем из (11.18), (11.19) и (11.21):
получаем из (11.18), (11.19) и (11.21):
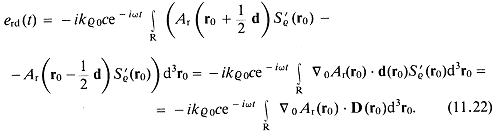
Из сравнения (11.10), (11.15) и (11.17) видно, что члены выражения (11.10) можно интерпретировать как волны давления от распределений монополей и диполей, если положить
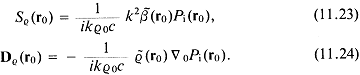
Подставляя эти выражения в (11.21) и (11.22) и интегрируя, получаем напряжение на выходе приемного преобразователя — отклик на волны давления от рассеивателей (эритроцитов), находящихся в области R:
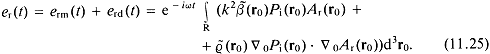
Эту формулу можно переписать в общем виде, так как известно, что вид функции чувствительности монополя Лг(го) совпадает с общим выражением для поля давления Pi(r0) излучателя — это следует из принципа взаимности [27]. Обычно далее вводится упрощение — рассматривается дальняя зона, или плоские волны. При этом
![]()
где Gt(r0) — действительная функция, kt — волновой вектор поля излучателя, ![]() — постоянная. Такой же вид имеет и Ar(r0). Однако доплеровские ультразвуковые приборы часто применяют для исследования кровеносных сосудов в ближнем поле излучателя, где могут стать существенными отклонения от модели плоских волн [1, 36]. Часто применяются и фокусирующие излучатели. Это означает, что направление волнового вектора меняется вдоль оси пучка; учтем это, введя зависимость волнового вектора от координат. Тогда в общем виде
— постоянная. Такой же вид имеет и Ar(r0). Однако доплеровские ультразвуковые приборы часто применяют для исследования кровеносных сосудов в ближнем поле излучателя, где могут стать существенными отклонения от модели плоских волн [1, 36]. Часто применяются и фокусирующие излучатели. Это означает, что направление волнового вектора меняется вдоль оси пучка; учтем это, введя зависимость волнового вектора от координат. Тогда в общем виде
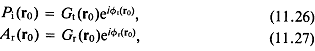
где ![]() для плоской волны (то же и для
для плоской волны (то же и для ![]() ). Отметим, что размерности ARr(r0) и Pi(r0) не совпадают по определению (то же для Gt(r0) и Gr(r0)).
). Отметим, что размерности ARr(r0) и Pi(r0) не совпадают по определению (то же для Gt(r0) и Gr(r0)).
Два предыдущих уравнения можно переписать в виде
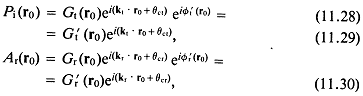
где
![]()
Величины kt и кг — волновые векторы падающего и рассеянного полей в приближении плоских волн; ![]() — разности фаз между истинными полями и полями, полученными в приближении плоских волн. Таким образом,
— разности фаз между истинными полями и полями, полученными в приближении плоских волн. Таким образом,
![]()
представляют собой флуктуации комплексной амплитуды, учитывающие изменения направления волнового вектора.
Чтобы вычислить дипольный член в подынтегральном выражении (11.25), необходимо знать градиенты Pi(r0) и Аг(г0).
Из выражения (11.28) получаем
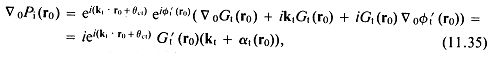
где
![]()
представляет собой малую поправку к kt в амплитудном члене (11.35), вызванную изменением направления волнового вектора и изменением Gt(r0).
Аналогичный вид имеет и ![]() . Тогда
. Тогда
![]()
где
![]()
- волновой вектор, направленный по биссектрисе угла между осями падающего и отраженного пучков,
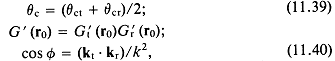
где ![]() - угол между осями обоих пучков,
- угол между осями обоих пучков,
![]()
Подставляя (11.29), (11.30) и (11.37) в (11.25), получаем
![]()
где
![]()
Предположим теперь, что кровь движется, а ![]() и
и ![]() зависят от времени. Зависимость этих величин от времени можно ввести на этом этапе, так как скорость кровотока много меньше скорости звука поэтому
зависят от времени. Зависимость этих величин от времени можно ввести на этом этапе, так как скорость кровотока много меньше скорости звука поэтому ![]() и
и ![]() изменяются незначительно в процессе рассеяния.
изменяются незначительно в процессе рассеяния.
после демодуляции остается огибающая принятого сигнала, имеющая вид (см. (11.42)):
![]()
Автокорреляционная функция доплеровского сигнала имеет вид
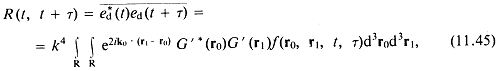
где черта означает усреднение по времени, звездочка — комплексное сопряжение, а
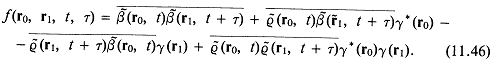
Предположим, что статистические свойства ![]() и
и ![]() не зависят от времени и координат (справедливость этого предположения мы обсудим ниже), поэтому усреднение по времени можно заменить усреднением по ансамблю. Кроме того, в плотном случайном скоплении эритроцитов, каждый из которых большую часть времени взаимодействует лишь с соседними, радиус корреляции
не зависят от времени и координат (справедливость этого предположения мы обсудим ниже), поэтому усреднение по времени можно заменить усреднением по ансамблю. Кроме того, в плотном случайном скоплении эритроцитов, каждый из которых большую часть времени взаимодействует лишь с соседними, радиус корреляции ![]() и
и ![]() (и, следовательно, функции J) порядка диаметра эритроцита, т. е. много меньше характерного масштаба изменений остальных членов подынтегрального выражения (11.45). При этом f можно представить в виде дельта-функции с объемом bv порядка объема эритроцита.
(и, следовательно, функции J) порядка диаметра эритроцита, т. е. много меньше характерного масштаба изменений остальных членов подынтегрального выражения (11.45). При этом f можно представить в виде дельта-функции с объемом bv порядка объема эритроцита.
Наконец, так как диффузия, изменяющая распределение эритроцитов, проявляется при скоростях, много меньших рассматриваемых скоростей кровотока [9], каждый элементарный объем крови остается неизменным во время прохождения через пучок. Тогда объем, координата которого в момент времени t была r0, в момент времени t + ![]() окажется в точке r0 + V(r0), где V(r0) — скорость кровотока.
окажется в точке r0 + V(r0), где V(r0) — скорость кровотока.
Отсюда следует, что уравнение (11.46) можно записать в виде
![]()
Подставляя его в (11.45) и интегрируя по r1 получаем
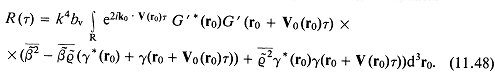
Отметим, что предположение о независимости статистических свойств ![]() и
и ![]() привело к независимости автокорреляционной функции от t.
привело к независимости автокорреляционной функции от t.
Вычислим доплеровский спектр мощности ![]() как преобразование Фурье от автокорреляционной функции:
как преобразование Фурье от автокорреляционной функции:
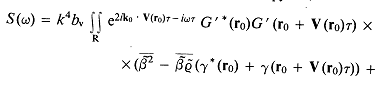
![]()
Ограничимся теперь рассмотрением течения с параллельными линиями тока и выберем декартову систему координат так, чтобы вектор скорости был параллелен оси х. Тогда скорость будет зависеть только от у и z. Уравнение (11.49) преобразуется к виду
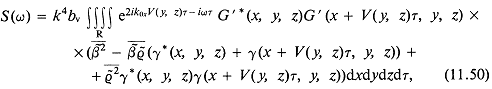
где ![]() _ x-компонента волнового вектора k0. Отметим, что индекс «0» у координат опущен, т. е. r0 = (х, у, z).
_ x-компонента волнового вектора k0. Отметим, что индекс «0» у координат опущен, т. е. r0 = (х, у, z).
Разложим спектр на составляющие S (![]() , у, z), принадлежащие различным линиям тока, и получим
, у, z), принадлежащие различным линиям тока, и получим
![]()
где Ryz — границы области рассеяния R в направлениях у и z, определяемые размерами кровеносного сосуда и шириной пучка (или только сосудом, если пучок его перекрывает). Под шириной пучка здесь подразумевается расстояние между точками, в которых G'(r) становится пренебрежимо малой. Отсюда
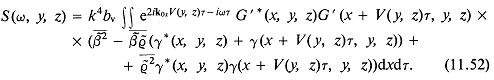
Отметим, что пределы в интеграле по х можно заменить на ±![]() , так как ось сосуда параллельна оси х и размер рассеивающей области R в этом направлении ограничивается функцией G(x, у, z).
, так как ось сосуда параллельна оси х и размер рассеивающей области R в этом направлении ограничивается функцией G(x, у, z).
Чтобы привести интеграл (11.52) к удобному виду, умножим подынтегральное выражение на ![]() , сделаем замену переменной х= V(y, z)t' и умножим на
, сделаем замену переменной х= V(y, z)t' и умножим на ![]() . Тогда
. Тогда
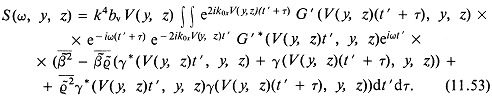
Чтобы далее не сохранять слишком много членов, заметим, что это выражение можно представить как сумму трех интегралов, содержащих (![]() ). Первый из них имеет вид
). Первый из них имеет вид
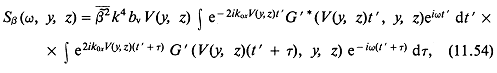
или
![]()
где ![]() означает преобразование Фурье. Это выражение можно переписать в виде
означает преобразование Фурье. Это выражение можно переписать в виде
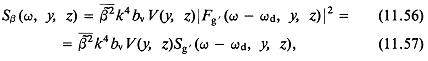
где
![]()
— доплеровская частота в приближении плоских волн, в — угол между векторами скорости и биссектрисой угла между падающим
и отраженным пучками.
Аналогично из (11.53) для интеграла, содержащего ![]() , имеем
, имеем
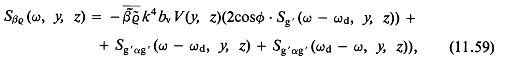
где ![]() — взаимная спектральная плотность энергии:
— взаимная спектральная плотность энергии: ![]()
Здесь ![]() разложено на составляющие с использованием выражения (11.43) и учтено известное свойство [25]
разложено на составляющие с использованием выражения (11.43) и учтено известное свойство [25]
![]()
Интеграл из (11.53), содержащий ![]() ,
,
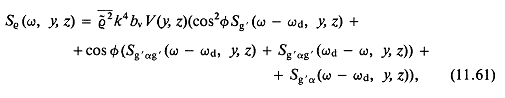
где
![]()
Объединяя (11.57), (11.59) и (11.61), получаем
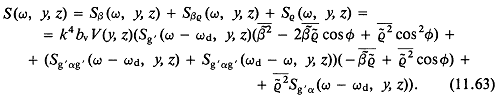
Зачастую можно пренебречь составляющими спектра, содержащими малую величину а. Главный член в выражении для спектра равен
![]()
где
![]()
Если в области пересечения сосуда с пучком постоянны радиус корреляции bv, среднеквадратичная плотность и сжимаемость крови, то С — постоянный коэффициент. Это условие будет исследовано далее.
Из уравнений (11.55)—(11.58) видно, что ![]() — это спектр сигнала
— это спектр сигнала
![]()
a
![]() — спектр сигнала
— спектр сигнала ![]() , сдвинутого по частоте на
, сдвинутого по частоте на ![]()
Раскладывая G' на амплитудные и фазовые множители (см. уравнения (11.33), (11.34) и (11.39)) и приводя подобные члены в выражениях для падающего и отраженного пучков, получаем
![]()
где
![]()
Комплексная функция чувствительности
![]()
характеризует изменение отклонений амплитуды и фазы от их значений в приближении плоских волн для случая точечного рассеивателя.
плоской волны. В этом случае
![]()
где k'х(х)— разность между х-компонентой волнового вектора в точке х и аналогичной величиной, полученной в приближении плоских волн, k0х. Если, кроме того, представить k'х(х) в виде степенного ряда, в котором достаточно учесть лишь члены нулевого и первого порядков, т. е.
![]()
то справедливо соотношение
![]()
Таким образом, если в центре пучка волновой вектор совпадает с приближением плоской волны и линия тока проходит через центр (ось) пучка, то а0 = 0. Если же линия тока не проходит через ось пучка, то величина а0 может быть достаточно большой, а содержащий ее член будет представлять смещение частоты доплеровского сигнала в центре линии тока в диапазоне ![]() от
от ![]() .
.
В обоих случаях временная зависимость, определяющая форму спектра (согласно (11.73) и (11.76)), будет иметь вид
![]()
Если чувствительность вдоль линии тока можно аппроксимировать гауссовой функцией, т. е. представить ее как
![]()
то временная зависимость примет вид
![]()
Используя результаты из теории радиолокации [41], находим спектр мощности для этого сигнала:
![]()
где
![]()
Таким образом, спектр имеет гауссову форму с шириной
![]()
Первый член в скобках определяет времяпролетное уширение, второй — уширение из-за расходимости пучка1).
Если пучок широкий и времяпролетным уширением можно пренебречь по сравнению с уширением из-за расходимости, то можно воспользоваться общим правилом [41]: спектр ![]() функции
функции
![]() , где
, где ![]() — нелинейная функция, при ширине
— нелинейная функция, при ширине ![]() , много большей ширины спектра модуля функции
, много большей ширины спектра модуля функции ![]() , можно представить приближенно в виде
, можно представить приближенно в виде
![]()
Следует особо подчеркнуть, что вышеприведенные результаты справедливы лишь в некоторых частных случаях.
11.5.2. СПЕКТР ИМПУЛЬСНО-ДОПЛЕРОВСКОГО СИГНАЛА
При анализе характеристик импульсно-доплеровских приборов необходимо вначале сделать некоторые упрощения, а затем обсудить влияние возможных отклонений от них. Как было показано выше (см., например, (11.63)), мощность рассеянного эритроцитами сигнала пропорциональна четвертой степени модуля волнового вектора (частоты). Здесь мы будем предполагать, что спектр излученного импульса достаточно узок, т. е. импульс имеет достаточную длительность, так что в пределах ширины спектра рассеяние не зависит от частоты. Будем предполагать, что любой участок импульса рассеивается так же, как и непрерывное излучение, но амплитуда сигнала зависит от времени. Предположим также, что вне оси пучка форма импульса нигде не меняется, т. е. поведение импульса описывается функцией расстояния вдоль оси пучка. В этом случае
1) Как показано в работе Newhouse U. L., Furgason Е. S., Johnson G. Е., Wolf D. Л. The Dependence of Ultrasound Doppler Bandwidth on Beam Geometry, IEEE Trans. Sonics Ultrason., SU-27, 50—59 (1980) — оба этих вида уширения связаны с одним и тем же физическим явлением — неопределенностью волнового вектора, и их разделение весьма условно. — Прим. перев.
для импульсно-доплеровского прибора формулу (11.42) можно переписать так:
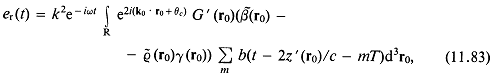
где T—период следования импульсов, z' (r0) — расстояние вдоль оси пучка от преобразователя до точки r0, b(t) — огибающая излученного импульса с учетом искажений, вносимых приемным трактом.
Существует множество различных демодуляторов для импульсно-доплеровских приборов. Все они чувствительны к принимаемому сигналу лишь в течение короткого отрезка времени после каждого излученного импульса. Найдем спектр доплеровского сигнала, получаемого при использовании одного из таких демодуляторрв (для других демодуляторов спектры получаются аналогично).
Устройство рассматриваемого демодулятора показано на рис. 11.7. Принятый сигнал er(t) перемножается с опорным сигналом ![]() и после прохождения фильтра низких частот с импульсным откликом h' (t) (или передаточной функцией Н' (
и после прохождения фильтра низких частот с импульсным откликом h' (t) (или передаточной функцией Н' (![]() )) стробируется по времени с задержкой T1 относительно каждого момента излучения импульса (длительность строба
)) стробируется по времени с задержкой T1 относительно каждого момента излучения импульса (длительность строба ![]() выбирают много меньше характерного времени изменения h' (t)). Затем сигнал поступает на НЧ-фильтр с импульсным откликом h’(t) (или передаточной функцией H(
выбирают много меньше характерного времени изменения h' (t)). Затем сигнал поступает на НЧ-фильтр с импульсным откликом h’(t) (или передаточной функцией H(![]() )). Тогда с учетом (11.83) сигнал на выходе демодулятора можно представить в виде
)). Тогда с учетом (11.83) сигнал на выходе демодулятора можно представить в виде
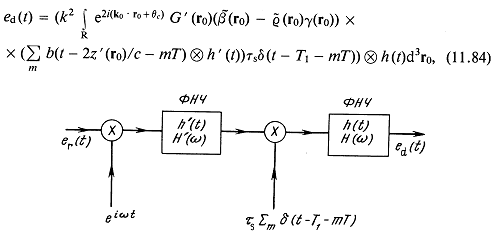
Рис. 11.7. Демодулятор для импульсно-доплеровского прибора.
где ![]() — дельта-функция Дирака. Так как
— дельта-функция Дирака. Так как ![]() и
и ![]() — медленно меняющиеся функции, а характерные времена изменения функций h'(t) и b(t) сравнимы (-1 мкс), фильтр после перемножителя будет существенно сказываться лишь на b(t). Полагая
— медленно меняющиеся функции, а характерные времена изменения функций h'(t) и b(t) сравнимы (-1 мкс), фильтр после перемножителя будет существенно сказываться лишь на b(t). Полагая
![]()
и используя фильтрующее свойство дельта-функции, получаем
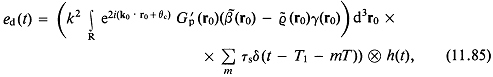
Из сравнения со случаем сигнала в ДПНИ (уравнение (11.44)) видно, что импульсно-доплеровский сигнал также содержит множитель вида
![]()
В случае импульсного сигнала функция распределения чувствительности по полю (уравнение (11.86)) включает сомножитель ![]() , описывающий изменение чувствительности вдоль пучка (рис.11.8). Действие остальных сомножителей в уравнении (11.85) можно проследить, подставляя в него выражение (11.87) и выполняя преобразование Фурье:
, описывающий изменение чувствительности вдоль пучка (рис.11.8). Действие остальных сомножителей в уравнении (11.85) можно проследить, подставляя в него выражение (11.87) и выполняя преобразование Фурье:
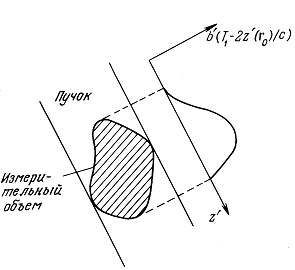
Рис. 11.8. Измерительный объем и изменение чувствительности вдоль оси пучка в импульсно-доплеровском приборе.
![]()
здесь ![]() и
и ![]() обозначают фурье-образы функций ed(t) и fp(t), использованы также основные свойства преобразования Фурье [25]. Свертка /р(со) с периодической б-функцией приводит к периодическому повторению спектра Fp(co) вдоль оси
обозначают фурье-образы функций ed(t) и fp(t), использованы также основные свойства преобразования Фурье [25]. Свертка /р(со) с периодической б-функцией приводит к периодическому повторению спектра Fp(co) вдоль оси ![]() (рис. 11.9). Чтобы устранить этот эффект, применяют фильтр, пропускающий сигналы только в полосе угловых частот от -
(рис. 11.9). Чтобы устранить этот эффект, применяют фильтр, пропускающий сигналы только в полосе угловых частот от -![]() /Т до
/Т до ![]() /Т Идеальная передаточная функция H(
/Т Идеальная передаточная функция H(![]() ) показана на рис. 11.9. Однако реализуемая на практике характеристика фильтра будет иметь более пологие скаты на границах диапазона.
) показана на рис. 11.9. Однако реализуемая на практике характеристика фильтра будет иметь более пологие скаты на границах диапазона.
Следует отметить, что полоса однозначно определяемых частот сигналов ограничена диапазоном (-1/2T, 1/2T), т.е. величиной ±Fr / 2 (Fr — частота повторения импульсов). Если спектр выходит за эти пределы, то его «внешняя» часть все же попадает в тот же диапазон, но уже с частотами другого знака. Это общее для всех сигналов с периодической выборкой явление называется маскировкой. При заданной частоте повторения импульсов единственный способ согласовать доплеровскую частоту с рабочим диапазоном — увеличить угол между осью пучка и вектором скорости. На частоту повторения импульсов накладывается ограничение: импульс должен пройти расстояние до исследуемого сосуда и назад до момента излучения следующего импульса. Таким образом, максимальная глубина локации равна
![]()
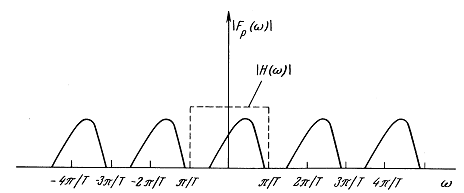
Рис. 11.9. Огибающая спектра доплеровских частот на выходе демодулятора импульсно-доплеровского прибора до НЧ-фильтра (|Fp(![]() )|) и частотная характеристика идеального фильтра, включаемого после демодуляции (|H(
)|) и частотная характеристика идеального фильтра, включаемого после демодуляции (|H(![]() )|).
)|).
Ограничение на доплеровскую частоту ![]() приводит к ограничению максимальной измеряемой скорости кровотока (см. (11.6)):
приводит к ограничению максимальной измеряемой скорости кровотока (см. (11.6)):
![]()
Исключая Т из (11.89) и (11.90), получаем наибольшую величину произведения скорости на дальности:
![]()
Из (11.88) получаем спектр мощности
![]()
где S(![]() ) — спектр ДПНИ, функция чувствительности которого модифицирована согласно (11.86). Так как обычно
) — спектр ДПНИ, функция чувствительности которого модифицирована согласно (11.86). Так как обычно ![]() мкс,
мкс, ![]() мкс, показатель
мкс, показатель ![]() может быть очень малым, поэтому обычно для поддержания достаточного уровня сигнала на выходе фильтра, следующего за перемножителем, вместо устройства выборки используют устройство выборки-хранения. При этом
может быть очень малым, поэтому обычно для поддержания достаточного уровня сигнала на выходе фильтра, следующего за перемножителем, вместо устройства выборки используют устройство выборки-хранения. При этом
Выполняя преобразование Фурье над ed(t) и учитывая, что H(![]() ) подавляет повторения Fр(
) подавляет повторения Fр(![]() ) и устраняет неоднозначность, получаем спектр сигнала
) и устраняет неоднозначность, получаем спектр сигнала
![]()
где Sa(x) = sinx/x — функция выборки. Параметр ![]() существенно влияет на частотную характеристику, так как он равен 1 при
существенно влияет на частотную характеристику, так как он равен 1 при ![]() = 0 и спадает до 0,41 на максимально возможной доплеровской частоте
= 0 и спадает до 0,41 на максимально возможной доплеровской частоте ![]() /Т. Для сохранения равномерности характеристик необходимо подобрать такой вид функции H(
/Т. Для сохранения равномерности характеристик необходимо подобрать такой вид функции H(![]() ), чтобы произведение
), чтобы произведение ![]() было постоянным вплоть до максимальной ожидаемой доплеровской частоты.
было постоянным вплоть до максимальной ожидаемой доплеровской частоты.
11.5.3. ФОРМА СПЕКТРА ДОПЛЕРОВСКОГО СИГНАЛА
Очевидно, в общем случае форма спектра доплеровских частот определяется как полем скоростей, так и характеристиками ультразвукового пучка. Однако если уширение спектра, обусловленное пучком, пренебрежимо мало (большие времена пролета и малые изменения волнового вектора), то спектральную составляющую от каждой линии тока можно представить как б-функцию на доплеровской частоте, соответствующей пересечению центра пучка с этой линией тока, а ее амплитуду — пропорциональной мощности сигнала. В этом случае из уравнений (11.51) и (11.71) получаем
![]()
где доплеровская частота связана со скоростью выражением (11.58). Количественно спектр можно оценить, разбивая ось частот на отрезки и суммируя вклады от линий тока с весами W(y, z).
Дальнейшие упрощения можно сделать, если W(y, z) — постоянная величина (W) по сечению кровеносного сосуда, а поле скоростей осесимметрично. В этом случае, переходя к цилиндрической системе координат с продольной осью, совпадающей с осью сосуда (при этом поля скоростей и доплеровских частот зависят от радиальной координаты rа), получаем
![]()
где ![]() , a—радиус сосуда.
, a—радиус сосуда.
Если ![]() — монотонная функция и существует обратная ей функция
— монотонная функция и существует обратная ей функция ![]() , то, заменяя переменную в интеграле (11.97) на
, то, заменяя переменную в интеграле (11.97) на ![]() , получаем
, получаем
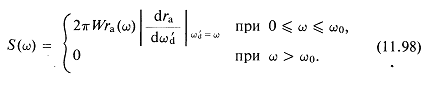
Например, если профиль скорости представляется в виде
![]()
(т. е. «сплющенность» профиля с ростом п увеличивается; параболическому профилю отвечает п = 2), то
![]()
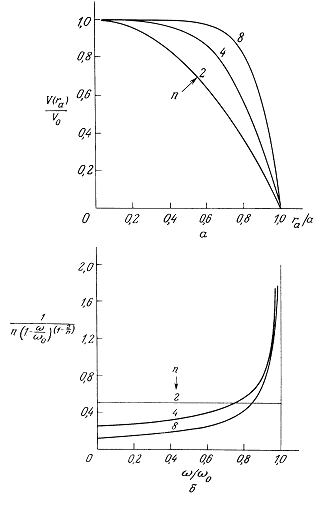
Рис. 11.10. а — Профили скорости потока вида V(ra) = = Vо(1 - (rа/a)n); б — соответствующие формы спектров без учета искажений, вносимых характеристиками пучков.
где ![]() 0 — доплеровская частота, соответствующая скорости V0 в центре сосуда, и
0 — доплеровская частота, соответствующая скорости V0 в центре сосуда, и
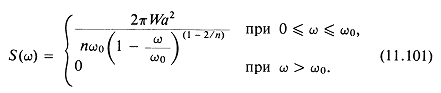
Некоторые примеры приведены на рис. 11.10. Видно, что спектр для параболического профиля потока равномерен вплоть до максимальной частоты. Как и ожидалось, для плоского профиля энергия сосредоточена на высоких частотах. Для «поршневого» потока (скорость по сечению постоянна) спектр представляется 5-функцией на частоте ![]() .
.
В описанном примере требуется, чтобы пучок охватывал сосуд целиком; тогда функцию W(y, z) можно считать постоянной величиной. Если пучок более узкий, то теряется мощность сигнала от медленно движущихся областей кровотока у стенок сосуда, поэтому увеличивается доля мощности в спектре на высоких частотах, соответствующих более высоким скоростям в центре сосуда. Если размеры измерительного объема импульсно-доплеровского прибора малы по сравнению с диаметром сосуда, будет зарегистрирован узкий доплеровский спектр, характеризующий интервал скоростей линий тока, проходящих через этот объем.
Для того чтобы измеренная средняя частота всегда была пропорциональна средней скорости, необходимо выполнение трех условий. Во-первых, снижение доли низкочастотных компонент спектра от медленного кровотока из-за ВЧ-фильтра (см. с. 401) должны быть пренебрежимо малы. Во-вторых, доплеровские сигналы от всех линий тока должны иметь одинаковую мощность, т. е. функция W(y, z) должна быть постоянна по сечению сосуда. В-третьих, средние частоты в спектре от каждой линии тока должны быть равны доплеровской частоте на оси пучка (точнее, значению, полученному в приближении плоских волн). Последнее условие означает, что спектры от каждой линии тока симметричны относительно доплеровской частоты на оси пучка.
Не существует простых общих требований к комплексной функции чувствительности пучка, позволяющих обеспечить такую симметрию. Однако существуют два условия, при которых будет формироваться симметричный спектр. Во-первых, так как спектр мощности действительной функции всегда симметричен [25], это условие выполняется, если можно пренебречь изменениями волнового вектора и положить ![]() . Во-вторых, записав в явном виде спектр мощности для линии тока как преобразование Фурье от комплексной функции чувствительности пучка, можно убедиться, что спектр от линии тока симметричен, если функция чувствительности пучка G(x) симметрична, а
. Во-вторых, записав в явном виде спектр мощности для линии тока как преобразование Фурье от комплексной функции чувствительности пучка, можно убедиться, что спектр от линии тока симметричен, если функция чувствительности пучка G(x) симметрична, а ![]() — четная функция.
— четная функция.
Одно из главных применений методов доплеровской ультразвуковой локации при исследовании кровотока — обнаружение его нарушений, вызванных поражениями стенок сосуда [7, 42]. Возмущения в потоке приводят к расширению диапазонов скоростей и углов между вектором скорости и осями ультразвуковых пучков и, следовательно, к увеличению диапазона доплеровских частот, т. е. к уширению спектра сигнала. Кроме того, отмечалось значительное увеличение мощности сигнала при появлении турбулентных потоков [24, 38]. Некоторые возможные механизмы этого явления обсуждаются в работе [2]. Возможно, что случайные пульсации скорости в турбулентном потоке крови увеличивают диапазон концентраций форменных элементов из-за различных плотностей эритроцитов и плазмы. Это будет приводить к увеличению параметров ![]() и, следовательно к увеличению мощности сигнала. Кроме того, предположение о
и, следовательно к увеличению мощности сигнала. Кроме того, предположение о ![]() -коррелированности
-коррелированности ![]() и
и ![]() с объемом корреляции bv (см. (11.47)) несправедливо при больших случайных ускорениях, хотя точная степень влияния этого фактора на мощность сигнала пока не ясна.
с объемом корреляции bv (см. (11.47)) несправедливо при больших случайных ускорениях, хотя точная степень влияния этого фактора на мощность сигнала пока не ясна.
Ранее мы пренебрегали спектральными составляющими, содержащими параметр ![]() (см. (11.63)). Этот вопрос не был исследован, и мы можем лишь строить предположения о случаях, когда они могли бы быть существенными. Из (11.63) видно, что содержащие а члены могут быть существенны там, где функции G(r0) и
(см. (11.63)). Этот вопрос не был исследован, и мы можем лишь строить предположения о случаях, когда они могли бы быть существенными. Из (11.63) видно, что содержащие а члены могут быть существенны там, где функции G(r0) и ![]() сильно меняются на расстояниях, сравнимых с длиной волны. На практике быстрые изменения G(r0) могут появиться во френелевской (ближней) зоне преобразователей. Быстрые изменения как G(r0), так и
сильно меняются на расстояниях, сравнимых с длиной волны. На практике быстрые изменения G(r0) могут появиться во френелевской (ближней) зоне преобразователей. Быстрые изменения как G(r0), так и ![]() (го) могут также появляться в полях сильно фокусирующих преобразователей. Затухание ультразвука в крови может оказывать заметное влияние при исследовании больших сосудов на высоких частотах, что на практике встречается редко.
(го) могут также появляться в полях сильно фокусирующих преобразователей. Затухание ультразвука в крови может оказывать заметное влияние при исследовании больших сосудов на высоких частотах, что на практике встречается редко.
Недавно опубликованные результаты наблюдений изменения мощности доплеровского сигнала в течение кардиоцикла [33] заставляют сомневаться в справедливости предположения о независимости объема корреляции bv и параметров ![]() от времени. Этот эффект еще до конца не исследован и не объяснен. При малых скоростях имеет место изменение обратного рассеяния, связанное с зависимостью агрегации клеток от потока [39], но характерное время этих изменений, вероятно, слишком велико, чтобы объяснить такое их поведение за время кардиоцикла. Возможно, что эритроциты могут временно упорядочиваться, тем самым увеличивая объем корреляции bv. Если эти изменения мощности доплеровского сигнала ограничиваются относительно медленными изменениями по всему кардиоциклу, то полученные результаты еще остаются справедливыми. Однако если изменения вызваны ускорением и торможением элементов крови, то, поскольку эти характеристики изменяются по сечению сосуда (в центре сильнее, чем у стенок), следует ожидать изменения мощности по сечению сосуда. Это могло бы существенно повлиять на полученные результаты. Константа С в (11.65) должна зависеть от координат у и z и влиять на форму спектра через весовую функцию для линий тока W(y, z) (выражение (11.72)). Она также должна меняться со временем в течение кардиоцикла.
от времени. Этот эффект еще до конца не исследован и не объяснен. При малых скоростях имеет место изменение обратного рассеяния, связанное с зависимостью агрегации клеток от потока [39], но характерное время этих изменений, вероятно, слишком велико, чтобы объяснить такое их поведение за время кардиоцикла. Возможно, что эритроциты могут временно упорядочиваться, тем самым увеличивая объем корреляции bv. Если эти изменения мощности доплеровского сигнала ограничиваются относительно медленными изменениями по всему кардиоциклу, то полученные результаты еще остаются справедливыми. Однако если изменения вызваны ускорением и торможением элементов крови, то, поскольку эти характеристики изменяются по сечению сосуда (в центре сильнее, чем у стенок), следует ожидать изменения мощности по сечению сосуда. Это могло бы существенно повлиять на полученные результаты. Константа С в (11.65) должна зависеть от координат у и z и влиять на форму спектра через весовую функцию для линий тока W(y, z) (выражение (11.72)). Она также должна меняться со временем в течение кардиоцикла.
При анализе работы импульсно-доплеровского прибора мы предполагали, что длительность импульса достаточно велика, так что можно просто обобщить теорию ДПНИ. На практике излучаемый импульс имеет конечную ширину полосы частот, тем большую, чем меньше длительность импульса. При увеличении относительной ширины полосы частотно-зависимые множители, которые мы полагали постоянными, могут существенно изменяться и влиять на результат. Зависимость мощности рассеянного сигнала от четвертой степени частоты увеличивает среднюю частоту спектра импульса, а рост затухания с частотой уменьшает ее [23, 30]. Дополнительная сложность вызвана тем, что высокочастотные составляющие излучаемого импульса распределены неравномерно по его длительности — сконцентрированы на его краях.
Кроме того, частота излучаемого импульса может меняться в течение его длительности из-за особенностей его генерации. В начале импульса возбуждения преобразователь будет «звенеть» в течение нескольких периодов колебаний; при окончании импульса возбуждения преобразователь снова «звенит». Частоты «звона» в начале и в конце импульса могут отличаться из-за различия электрических нагрузок в возбужденном и невозбужденном состояниях.
Для коротких импульсов непригодно приближение, в котором функция чувствительности пучка для импульсно-доплеровского прибора равна функции чувствительности ДПНИ, умноженной на функцию продольной координаты пучка (см. (11.86)). Процесс установления колебаний в непрерывно возбуждаемом преобразователе после включения (в результате интерференции волн от различных участков преобразователя) занимает несколько периодов [11, 45]. Это означает, что поле импульсно-возбуждаемого преобразователя несколько меняется во время импульса. Кроме того, так как положение импульса в любой момент времени в сходящемся или расходящемся пучке (в дальней зоне или при фокусировке) зависит от радиальной координаты относительно точки схождения (расхождения) пучка, положение импульса на периферии поля будет отличаться от положения на оси при соответствующих значениях продольной координаты. Очевидно, что эта ошибка будет более существенной для коротких импульсов и для сильно сходящихся или расходящихся полей. Более полное рассмотрение этого вопроса приведено в разд. 2.3 при описании поля акустического импульса.
Влияние большинства отклонений от использованных предположений, сформулированных при построении теории доплеровского сигнала, можно в принципе проанализировать. Однако необходимо отметить, что учесть влияние отклонения от предположения об однородности акустического пути между преобразователями и кровотоком очень сложно даже в частных случаях и невозможно в общем виде. Прежде чем достичь сосуда, ультразвуковой пучок проходит через контактный гель, кожу, жировые и мышечные ткани, стенку сосуда. Все эти среды обладают несколько отличающимися акустическими свойствами, что вызывает преломление, отражение и рассеяние пучка. Заметные изменения акустических свойств, обусловленные, например, наличием газовых пузырьков в контактном геле или склеротических бляшек, могут вызывать такие искажения, что результаты приведенного выше анализа вообще станут неприменимы к реальным сигналам.
1. Aindow, J. D. & Cliivers, R. C. (1982). Measurement of the phase variation in the ultrasonic field. J. Phys. E. 15, 83—86.
2. Angelsen, B. A. J. (1980). A theoretical study of the scattering of ultrasound from blood. IEEE Trans. Biomed. Eng., BME-27, 61—67.
3. Atkinson, P. & Berry, M. V. (1974). Random noise in ultrasonic echoes diffracted by blood. J. Phys. A., 7, 1293—1302.
4. Atkinson, P. & Woodcock, J. P. (1982). Doppler ultrasound and its use in clinical measurement. Academic Press (London).
5. Baker, D. W. (1970). Pulsed ultrasonic blood fiow sensing. IEEE Trans. Son. Ultrason., SU-17, 170—185.
6. Barnes, R. W., Rittgers, S. E., & Putney, W. W. (1982). Real time Doppler spectrum analysis. Arch. Surg., Ill, 52—57.
7. Blackshear, W. M., Phillips, D. J., Thiele, B. L., Hirsch, J. H., Chikos, P. M., Marinelli, M. R., Ward, K. J., & Strandnes, D. E. (1979). Detection of carotid occlusive disease by ultrasonic imaging and pulsed Doppler spectrum analysis. Surgery, 86, 698—706.
8. Borodzinski, K., Filipczynski, I., Nowicki, A., & Powalowski, T. (1976). Quantitative transcutaneous measurements of blood flow in carotid artery by means of pulse and continuous wave Doppier methods. Ultrason. Med. Biol. 2, 189—193.
9. Brody, W. (1972). Theoretical analysis of the ultrasonic blood flowmeter. PhD thesis (Stanford University, USA).
10. Callagan, D. A., Rowland, Т. C, & Goldman, D. E. (1964). Ultrasonic Doppler observation of the fetal heart. Obstet. Gynec. 23, 637.
11. Christie, D. G. (1962). The distribution of pressure in the sound beams from probes used with ultrasonic flaw detectors. Materials Research, 86—97.
12. Coghlan, B. A. & Taylor, M. G. (1976). Directional Doppler technique for detection of blood velocities. Ultrason. Med. Biol. 2, 171—181.
13. Cross, G. & Light, L. H. (1974). Non-invasive intra-thoracic blood velocity measurement in the assessment of cardio-vascular function. Biomed. Eng., 9, 404—471.
14. De Jong, D. A., Megens, P. H. A., De Vlieger, M., Thon, H., & Holland, W. P. J. (1975). A directional quantifying Doppler system for measurement of transport velocity of blood. Ultrasonics 13, 138—141.
15. Eiknes, S. H., Brubakk, A. O., & Ulstein, M. K. (1980). Measurement of human fetal blood flow. Br. Med. J. 280, 283—284.
16. Fish,. P. J. (1975). Multichannel, direction-resolving Doppler angiography. Proc. 2nd Europ. Cong. Ultrason. Med., Munich, 153—159.
17. Fish, P. J. & Walters, D. (1977). The beam/vessel angle problem in Doppler flow measurement. In Non-invasive clinical measurement, (eds. D. E. M. Taylor & J. Whamond), Pitman Medical (London), 105—113.
18. Fish, P. J. (1981). A method of transcutaneous blood fiow measurement-accuracy considerations. In Recent advances in ultrasound diagnosis 3. (eds. A. Kurjak & A. Kratochwil) Excerpta Medica (Amsterdam), 110—115.
19. Flax, S. W, Webster, J. G., & Updike, S. J. (1973). Statistical evaluation of the Doppler ultrasonic blood flowmeter. Biomed. Sci. Instrum. 7, 201—222.
20. Gill, R. W. (1979). Pulsed Doppler with B-mode imaging for quantitative blood flow measurement. Ultrason. Med. Biol., 5, 223—235.
21. Gore, J. C. & Leeman, W. (1977). Ultrasonic backscattering from human tissue: a realistic model. Phys. Med. Biol., 22(2), 317—326.
22. Gosling, R. G., & King, D. H. (1975). Ultrasonic angiography. In Arteries and veins, (eds. A. W. Hascus & L. Adamson), Churchill Livingston, (Edinburgh), 61—98.
23. Holland, S. K., Orphanoudakis, S. C, & Jaffe, С. C. (1984). Frequency-dependent attenuation effects in pulsed Doppler ultrasound: experimental results. IEEE Trans. Biomed. Eng., BME-31, 626-631.
24. Kececioglu-Draelos, Z., Goldberg, S. J., Arias, J., & Sahn, D. J. (1981). Verification and clinical demonstration of the echo Doppler series effect and vortex shed distance. Circulation, 63(1), 1422—1428.
25. Lathi, B. P. (1968). An introduction to random signals and communication theory. International Textbook Co. (Scranton, USA).
26. Martin, T. R. P., Barker, D. C, Sherriff, S. В., & Prichard, D. R. (1980). Objective feature extraction applied to the diagnosis of carotid artery disease using a Doppler ultrasound technique. Clin. Phys. Physiol. Meas., 1, 71—81.
27. Morse, P M. & Ingard, K. U (1968). Theoretical acoustics. McGraw-Hill (New York).
28. Mozerskey, D. J., Hokanson, D. E., Sumner, D. S., & Strandness, D. E. (1972). Ultrasonic visualisation of the arterial lumen. Surgery 72, 253—259.
29. Newhouse, V. L., Bendick, P. J., & Varner, L. W. (1976). Analysis of transit time effects on Doppler flow measurement. IEEE Trans. Biomed. Eng., BME-23, 381—387.
30. Newhouse, V. L., Ehrenwald, A. R., & Johnson, G. F. (1977). The effect of Rayleigh scattering and frequency dependent absorption on the output spectrum of Doppler blood flowmeters. In Ultrasound in medicine vol. 3B. (eds. D. White & E. Brown). Plenum Press (New York and London), 1181—1191.
31. Peronneau, P. A., Bournat, J. P., Bugnon, A., Barbet, A., & Xhaard, M. (1974). Theoretical and practical aspects of pulsed Doppler flowmetry: real-time application to the measure of instantaneous velocity profiles in vitro and in vivo. In: Cardiovascular application of ultrasound, (ed. R. S. Reneman), North Holland (Amsterdam). 66—84.
32. Peronneau, P., Sandman, W, & Xhaard, M. (1977). Blood flow patterns in large arteries. In: Ultrasound in medicine. Vol. 3B, (eds. D. White & E. Brown), Plenum Press (New York), 1193—1208.
33. Phillips, P. W. (1985). Carotid artery imaging using continuous wave Doppler ultrasound. PhD thesis, University of London.
34. Robinson, H. P. (1978). Normal development in early pregnancy. In: Handbook of Clinical Ultrasound, (ed. M. de Vlieger), John Wiley (New York), 121—139.
35. Satomura, S. (1957). Ultrasonic Doppler method for the inspection of cardiac functions. J. acoust. Soc. Am. 29, 1181—1185.
36. Seki, H., Granato, A., & Truell, R. (1956). Diffraction effects in the ultrasonic field of a piston source and their importance in the accurate measurement of attenuation. J. acoust. Soc. Am., 28(2), 230—238.
37. Shung, К. K., Sigelman, R. A., & Reid, J. M. (1976). Scattering of ultrasound by blood. IEEE Trans. Biomed. Eng., BME-23, 460—467.
38. Shung, К. K. Yuan, Y. W, & Fei, D. Y. (1984). Effect of flow disturbance on ultrasound backscatter from blood. J. acoust. Soc. Am., 75(4), 1265—1272. 39. Sigel, В., Machi, J., Beitler, J. C, Justin, J. R., & Coelho, J. С. V. (1982). Variable ultrasound echogenicity in flowing blood. Science, 218, 1321—1323.
40. Skidmore, R., Woodcock, J. P., Wells, P. H. Т., Bird, D. R., & Baird, R. N. (1980).
Physiological interpretation of Doppler shift waveforms—III Clinical results. Ultrasound Med. Biol. 6, 227—231.
41. Skolnik, M. (1970). Radar Handbook. McGraw-Hill, (New York).
42. Spencer, M. P. & Reid, J. M. (1979). Quantitation of carotid stenosis with
continuous wave (CW) Doppler ultrasound. Stroke, 10, 236—330.
43. Stegall, H. R, Kardon, M. В., & Kemmerer, W. T. (1968). Indirect measurement of
arterial blood pressure by Doppler ultrasonic sphygmomamometry. J. Appl. Physiol., 25, 793—797.
44. Wells, P. N. T. (1977). Biomedical ultrasonics. Academic Press (London).
45. Weyns, A. (1980). Radiation field calculations of pulsed ultrasonic transducers. Ultrasonics, 183—188.
Монографии
Atkinson, P. & Woodcock, J. P. (1982). Doppler ultrasound and its use in clinical measurement. Academic Press (London).
Fry, F. J. (1978). Ultrasound: its applications in medicine and biology. Elsevier (Amsterdam).
Reneman, R. S. (1974). Cardiovascular applications of ultrasound. North Holland (Amsterdam).
Stipa, S., Cavallard, A. & Modini, C. (1984). Informatics and bioengineering in
medicine. Serono Symposia (Rome). Wells, P. N. T. (1977). Biomedical ultrasonics. Academic Press (London). Woodcock, J. P. (1977). Ultrasonics. Adam Hilger (Bristol).
Woodcock, J. P. (1975). Theory and practice of blood flow measurement. Butterworths (London).
БИОФИЗИКА УЛЬТРАЗВУКОВЫХ ЭФФЕКТОВ И ИХ ПРИМЕНЕНИЕ
БИОФИЗИКА УЛЬТРАЗВУКОВЫХ ЭФФЕКТОВ
Г. тер Хаар
Биофизика ультразвуковых эффектов как научное направление имеет дело с поиском логических и количественных объяснений ряда экспериментов, в которых было найдено, что облучение ультразвуком приводит к специфическим изменениям в живых клетках и тканях. По-видимому, первым, кто сделал такого рода наблюдения, был Ланжевен, который в 1917 г., испытывая разработанные им мощные гидроакустические излучатели, предназначенные для обнаружения подводных лодок, заметил повреждения у рыб, попавших в ультразвуковой пучок. Его наблюдения стимулировали замечательные биофизические исследования Вуда и Лумиса [139], которые, в свою очередь, привели к появлению множества работ большого числа авторов. К сожалению, во многих из этих работ нет серьезных попыток научно объяснить полученные эффекты.
В настоящей главе рассмотрены физические явления, которые действительно или предположительно ответственны за различные виды связей между воздействием ультразвука и биологическими эффектами.
В широком плане такие связи можно разделить на тепловые и нетепловые. В эмпирическом подходе такое разделение могло бы означать наличие или отсутствие преимущественной обусловленности наблюдаемых изменений повышением температуры при поглощении энергии ультразвука. С физически более удовлетворительной точки зрения, однако, именно само поглощение акустической энергии обусловлено взаимодействием ультразвука с биологическими тканями на молекулярном или макромолекулярном уровне. Если молекулы относительно малы и среда текучая, то энергия колебательных или вращательных движений, вызванных взаимодействием с акустической волной, не приводит к специфическим химическим или биологическим изменениям и быстро превращается в тепло. Такой процесс поглощения может быть охарактеризован как тепловой. В средах менее текучих или содержащих гигантские молекулы, или обладающих и той и другой характеристикой вместе, существует возможность нетепловых специфических эффектов. Количественную оценку этой ситуации можно получить, сравнивая некоторые параметры, характеризующие движение молекул, например их скорость, при акустических и тепловых колебаниях [11].
В плоской бегущей волне в акустическом поле скорость частиц среды определяется из выражения (1.177):
![]()
например, для интенсивности 10 Вт/см2 в воде это составляет ![]() = 37 см/с.
= 37 см/с.
Средняя же скорость частиц при тепловых колебаниях определяется из классического выражения как
![]()
где T—абсолютная температура, k постоянная Больцмана, m — масса частиц.
Здесь скорость частиц зависит от их массы и для молекул воды и ДНК с молекулярной массой 107 составляет ![]() = 3,8•104 и 52 см/с соответственно при 37°С.
= 3,8•104 и 52 см/с соответственно при 37°С.
Возможно, было бы интересно исследовать эту ситуацию, используя более сложный анализ, но и этот упрощенный подход подтверждает, что нетепловые механизмы в изложенном выше контексте если и возникают, то в системах, включающих комплексы больших молекул.
Сказанное выше касалось линейных систем, т. е. таких сред, где предполагается линейная зависимость деформации от приложенного акустического напряжения. Существуют и другие механизмы, для которых определяющим фактором являются нелинейные эффекты, в частности такие, где колебательная акустическая энергия трансформируется («выпрямляется») в энергию неколебательной природы. В строгом смысле генерация тепла вследствие поглощения ультразвука тоже пример подобной ситуации, но есть и другие примеры нетепловой природы. Важнейший из них—кавитация, которая будет детально рассмотрена в этой главе. Будет также показано, что акустическая энергия может трансформироваться в энергию поля сдвиговых напряжений стационарного течения жидкости или в энергию компонентов химических реакций.
Энергия, переносимая ультразвуковым пучком, затухает при прохождении ее через вязкую среду. Если в начале координат при х = 0 интенсивность плоской бегущей волны равна /о, то на расстоянии х она уменьшается до величины
![]()
где ![]() —коэффициент затухания по интенсивности (см. гл. 4). Таким образом, потери энергии исходного звукового пучка при его распространении на единичное расстояние, dl/dx, равны
—коэффициент затухания по интенсивности (см. гл. 4). Таким образом, потери энергии исходного звукового пучка при его распространении на единичное расстояние, dl/dx, равны ![]()
![]() . Как уже обсуждалось в разд. 4.2, коэффициент затухания,
. Как уже обсуждалось в разд. 4.2, коэффициент затухания, ![]() , состоит из двух компонент: одной, обусловленной поглощением,
, состоит из двух компонент: одной, обусловленной поглощением, ![]() а, и другой, обусловленной рассеянием,
а, и другой, обусловленной рассеянием, ![]() s. Энергия, рассеянная из основного пучка, может поглощаться в других местах ткани.
s. Энергия, рассеянная из основного пучка, может поглощаться в других местах ткани.
Чтобы оценить увеличение температуры ткани из-за затухания ультразвукового пучка, предположим, что вся энергия, потерянная исходным пучком, идет на нагревание ткани. Иначе говоря, предположим, что коэффициент затухания целиком обусловлен поглощением. Это достаточно разумное предположение, поскольку известные величины для ![]() а мягких тканей изменяются в пределах от 0,6
а мягких тканей изменяются в пределах от 0,6![]() до 0,9
до 0,9![]() . Скорость выделения тепла в единичном объеме Q определяется выражением
. Скорость выделения тепла в единичном объеме Q определяется выражением
![]()
Если из этого объема нет потерь тепла из-за теплопроводности, конвекции или излучения, то
![]()
где ![]() — плотность среды, С—теплоемкость, dT/dt—скорость увеличения температуры.
— плотность среды, С—теплоемкость, dT/dt—скорость увеличения температуры.
Рассмотрим, например, среду, для которой ![]() = 0,2 непер/см,
= 0,2 непер/см, ![]() = 1 г/см3 и C = 4,18 Дж/г°С. Эти величины приблизительно соответствуют параметрам печени при комнатной температуре и частоте 1 МГц.
= 1 г/см3 и C = 4,18 Дж/г°С. Эти величины приблизительно соответствуют параметрам печени при комнатной температуре и частоте 1 МГц.
В рассматриваемой среде при интенсивности ультразвука 1 Вт/см2 скорость увеличения температуры dT/dt составит 0,048 °С/с (2,88 °С/мин).
Можно оценить, какое влияние оказывает теплопроводность среды на конечную температуру, достигаемую при установлении равновесия. Найборгом [107] было показано, что устанавливающаяся в состоянии теплового равновесия разность температур между центром хорошо поглощающей сферы радиуса R (температурой Т0) и ее окружением (![]() ) равна
) равна
![]()
где k—теплопроводность. Используя уравнение (12.4), получим
![]()
При ![]() , ср. табл. 12.1).
, ср. табл. 12.1).
Таблица 12.1
|
Параметр |
Обозначение | |||
|
Теплопроводность |
k | |||
|
Теплоемкость |
С | |||
|
Коэффициент затухания (для 1 МГц) |
| |||
|
Коэффициент температуропроводности |
D | |||
|
*Данные для скелетной мышцы. | ||||
Таким образом, между центром поглощающей сферы радиусом 1 см и ее окружением устанавливается разность температур 22,7°С, в то время как для сферы радиусом 1 мм только 0,23°С. Характерное время достижения равновесия такой системой ![]() порядка R2/D, где D—коэффициент температуропроводности, D = к/дС. При R = 1 см
порядка R2/D, где D—коэффициент температуропроводности, D = к/дС. При R = 1 см ![]() = 70 с, а при R = 1 мм
= 70 с, а при R = 1 мм ![]() = 7 с.
= 7 с.
В табл. 12.1 представлены характерные величины теплопроводности, теплоемкости, коэффициента затухания и температуропроводности для воды и мягких тканей.
Используя простые уравнения распространения тепла, можно рассчитать, какой нагрев можно ожидать в системах, состоящих из тканей различных типов. Достоинство такого математического моделирования заключается в том, что оно позволяет предсказать влияние параметров ультразвука и тканей на получаемое распределение температур.
Простейшая модель ткани, используемая в работах [10, 53], представляет собой образец, состоящий из трех плоскопараллельных слоев различных биологических тканей (мышца, жир и кость). Распределение температуры внутри ткани описывается уравнением
![]()
где D—коэффициент температуропроводности.
Для системы, в которой имеются и источники тепла (мощностью Нв единице объема), и механизм охлаждения (![]() ), одномерное уравнение выглядит так:
), одномерное уравнение выглядит так:
![]()
где индексы относятся к i-м компонентам ткани.
Для экспоненциального затухания источник тепла, связанный с ультразвуком, в первом слое, например, задается следующим образом:
![]()
где ![]() 0—интенсивность звука, падающего на образец. Функция
0—интенсивность звука, падающего на образец. Функция ![]() , определяющая охлаждение, зависит от теплопроводности и кровотока в ткани, а значит, и от внешней температуры и от координаты. Вообще, с хорошим приближением можно записать так:
, определяющая охлаждение, зависит от теплопроводности и кровотока в ткани, а значит, и от внешней температуры и от координаты. Вообще, с хорошим приближением можно записать так:
![]()
где S, G — константы, Т0 — начальная температура и f(t) — функция времени, учитывающая, например, охлаждение за счет расширения кровеносных сосудов, которое происходит при достижении температурой некоторого порогового значения.
Уравнение (12.9) можно решить численно, используя метод конечных разностей [18]. В работе [10] показано, что использование этих уравнений приводит к хорошему согласию теории и эксперимента. Тер Хаар [53] исследовала влияние акустических параметров — частоты ультразвука, его интенсивности и коэффициента затухания — на распределение температуры. Рис. 12.1 показывает результаты этих вычислений для плоской волны при интенсивности 3 Вт/см2 и частоте 1 МГц; видно также влияние на температуру различных коэффициентов затухания в центральном слое исследуемого образца тканей. Этот пример иллюстрирует трудности, встречающиеся при оценке распределения температуры, которое может возникнуть при воздействии ультразвука на ткань с недостаточно известными акустическими свойствами. Представленный на рисунке разброс коэффициентов затухания соответствует данным, полученным Нассири с соавт. [95] при различной ориентации волокон скелетной мышцы. Подобные изменения распределения температуры могут происходить и при незначительном изменении кровотока через исследуемую ткань [69].
На рис. 12.2 приведено температурное распределение, которое было бы создано сферическим фокусирующим излучателем с фокусным расстоянием 15 см в образце ткани, помещенном на расстоянии 10 см от поверхности излучателя [59].
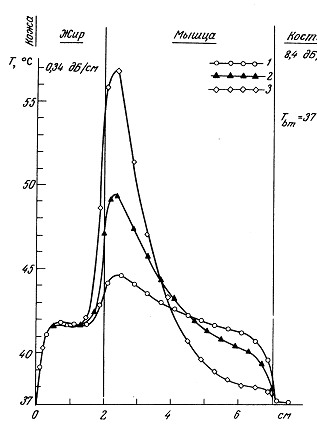
Рис. 12.1. Распределение температуры, рассчитанное для многослойной ткани, при облучении образца ультразвуком интенсивностью 3 Вт/см2 и частотой 1 МГц. Коэффициент затухания (дБ/см) для жира 0,34, для кости 8,4, для мышечной ткани: 1 — 1, 2 — 2, 3 — 4. Исходная температура 37°С.
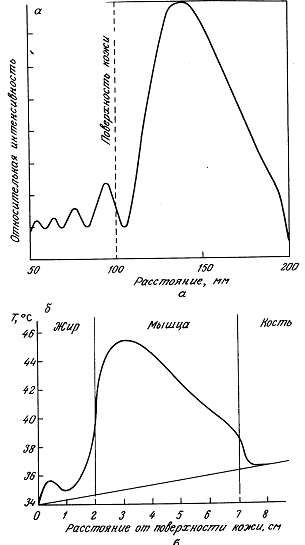
Рис. 12.2. а — Теоретическое распределение интенсивности для сферического фокусирующего преобразователя с фокусным расстоянием 150 мм и частотой 3 МГц; б—распределение температуры в многослойной ткани, возникающее при облучении образца полем, показанным на части я, когда поверхность кожи находится на расстоянии 10 см от фокусирующего излучателя по оси.
Увеличение температуры, вызванное ультразвуковыми диагностическими приборами, представляет особый интерес, поскольку непосредственно связано с безопасностью применения ультразвука. Вычисления показывают, что, например, для доплеровского прибора, работающего в непрерывном режиме на частоте 5 МГц со средней по пространству интенсивностью 0,1 Вт/см2, в центре его пучка радиусом 2,2 мм температура увеличивается на 1,8° С через 100 с [35, 36]. Для нефокусированного импульсного пучка с пиковой интенсивностью 20 Вт/см2 и длительностью импульса 10-6 с увеличение температуры за один импульс не превышает 3,3*10-6 оС; тогда как для интенсивности 200 Вт/см2 и длительности импульса 1 с достигает 33°С за импульс.
Как уже обсуждалось в гл. 1, в жидкой среде не могут распространяться поперечные (сдвиговые) волны. В мягких тканях, окружающих твердое включение, например кость, возникающие сдвиговые волны распространяются на ограниченное расстояние из-за того, что у них высокий коэффицент затухания. На поверхности раздела кость — мягкие ткани внутри тела продольные волны, распространяющиеся в кости, могут частично трансформироваться в поперечные, которые при своем распространении затем быстро поглотятся в мягких тканях. Это может приводить к локальному нагреву надкостницы — области, богатой нервными окончаниями. Если увеличение температуры достаточно большое, то возможно возникновение боли и необратимых повреждений.
12.1.2. ЭКСПЕРИМЕНТАЛЬНЫЕ НАБЛЮДЕНИЯ ТЕМПЕРАТУРНЫХ РАСПРЕДЕЛЕНИЙ
Сложная природа зависимости степени нагрева ткани от параметров ультразвука, самой ткани и ее окружения (см. разд. 12.1.1) порождает трудности при расчете распределений температуры с необходимой точностью. Имеющиеся публикации содержат очень мало информации об экспериментально измеренных распределениях температуры in vivo. В большинстве работ сообщается об экспериментах на собаках или свиньях, хотя и есть измерения, выполненные на тканях человека.
Температурные распределения, которые возникают в облучаемом объекте мягких тканей, могут значительно изменяться, если в этом объеме или на его границе есть кость. Бендер с соавт. [5] действовали ультразвуком на бедро собаки, в которое были имплантированы термопары. Использовался ультразвук частотой 800 кГц, общей мощностью 5 Вт с излучающей поверхностью 5 см2; длительность облучения составляла 2 мин. Измерения температуры проводились в надкостнице, в костном мозге и в мягких тканях между излучателем и бедренной костью. Данные из этой работы приведены на рис. 12.3. Наибольший нагрев зарегистрирован на поверхности кости. Данные о различной степени нагрева тканей ультразвуком приведены также в работе [78].
Леман с соавт. [74] выдвинули предположение, что нагрев надкостницы задает порог болевых ощущений при применении ультразвука и тем самым определяет пределы безопасности его применения.
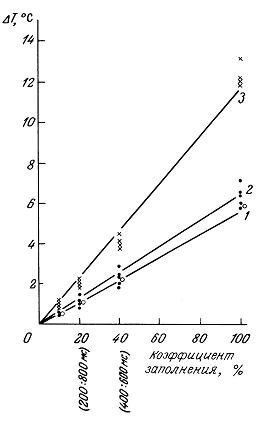
Рис. 12.3. Увеличение температуры, измеренное в бедре собаки. Облучение ультразвуком частотой 800 кГц, интенсивностью 1 Вт/см2 в течение 2 мин: 1 — мягкие ткани, 2 — костный мозг, 3— поверхность кости [5].
Они показали, что у пациентов со слоем мягких тканей толщиной менее 8 см над костью порог болевых ощущений достигался быстрее (при одной и той же интенсивности), чем у пациентов с более толстым слоем мягких тканей. Измерения температуры подтвердили, что этот болевой порог определялся нагревом поверхности кости. Это могло быть следствием трансформации энергии, обсуждавшейся ранее.
Леман с соавт. [77] сравнивали коротковолновую, микроволновую и ультразвуковую диатермию тазобедренного сустава. Было показано, что нагрев при максимально переносимых дозах коротковолнового и микроволнового облучения приводит к ожогам первой степени на коже и в подкожных тканях без заметного повышения температуры самого тазобедренного сустава. В то же время ультразвук дает адекватное увеличение температуры на кости без перегрева кожи.
Существует немного примеров исследования возможности применения ультразвука для нагрева мягких тканей, не содержащих костей, хотя это очень важно для применения в диатермии. Тер Хаар и Хоупвелл [56] провели замеры распределения температуры в мышечной ткани бедра свиньи. На рис. 12.4 приведены результаты этих измерений. Внизу показано нормальное (до нагрева) распределение температуры в мышечной ткани до глубины 4 см. Приведенные данные получены при усреднении по шести экспериментальным животным. Вверху показано распределение температуры, полученное в результате воздействия ультразвуком с частотой 0,75 МГц и интенсивностью 2 Вт/см2. Нормальной физиологической реакцией на подъем температуры является изменение кровотока. Объемный кровоток в ткани, который может быть вычислен из кривых охлаждения, полученных при выключении ультразвука, увеличивается в 2—3 раза по отношению к исходному при увеличении температуры до 40—45° С.
Ультразвуковой нагрев тканей до температур 42—44° С увеличивает также кровоток в бедренных артериях собаки [112].
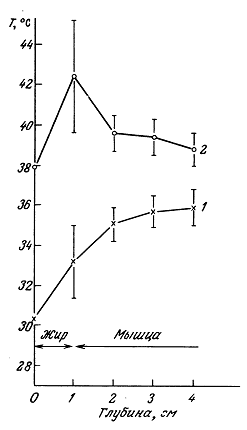
Рис. 12.4. Распределение температуры в бедре свиньи: 1 — исходная температура; 2 — при облучении ультразвуком частотой 0,75 МГц и средней по пространству интенсивностью 2 Вт/см2 [56].
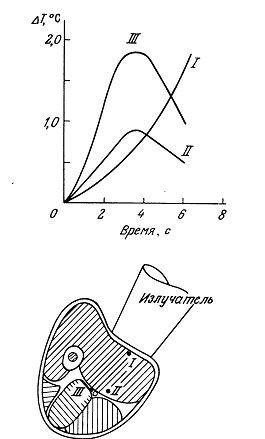
Рис. 12.5. Увеличение температуры в седалищном нерве мыши (III), мышечной ткани (II) и подкожных тканях (I) после облучения ультразвуком [117].
Розенбергер [117] показал, что при воздействии на седалищные нервы экспериментальных животных in situ ультразвуком интенсивностью 2 Вт/см2 и частотой 0,8—1 МГц нервные волокна нагрелись выше, чем окружающие их ткани (рис. 12.5). Это было также отмечено Герстеном [45]. Херрик [63] в экспериментах на крысах показал, что воздействие ультразвуком частотой 0,8—1 МГц, который не вызывает никаких видимых гистологических изменений в мышцах, окружающих нервные волокна, может приводить к повреждению самих нервных волокон. Характер этих повреждений такой же, как и при избыточном нагреве.
Хотя нагрев тканей за счет поглощения ультразвуковой энергии тканью хорошо известен, до сих пор с нужной полнотой не проведены научные исследования, которые позволили бы рассчитывать распределения температуры с необходимой точностью. Известно только, что кость или газовые включения в облучаемой ультразвуком мягкой ткани могут вызывать локальные нагревы или «горячие точки» из-за трансформации мод колебаний, отражений ультразвука или кавитационных эффектов (см. разд. 12.2). Следует уделять особое внимание макроструктуре облучаемой ткани, когда желательно вызвать тепловой эффект или, наоборот, необходимо его избежать.
В большинстве статей о химических и биологических эффектах ультразвука отсутствуют убедительные данные, дающие возможность выявить механизм его действия в каждом конкретном случае. Большая часть экспериментов (особенно при воздействии на жидкие среды) проводилась при условиях, когда возникновение кавитации как основного механизма было весьма вероятным. В то же время возможность экстраполяции этих результатов на условия, характерные для тканей млекопитающих, остается неясной. В этой ситуации очевидно, что хорошее объяснение явления кавитации, а также определяющих ее факторов и ограничений важно для достаточно ясного представления о предмете биофизики ультразвукового воздействия. Настоящий раздел как раз и посвящен изучению некоторых аспектов кавитации.
В литературе существует много определений кавитации. Неппирас [100] определяет кавитацию как явление, при котором в объеме жидкости образуется новая поверхность. Это широкое определение включает в себя кипение и бурную дегазацию. Апфель [2] определил кавитацию как образование одного или нескольких включений газа или полостей в жидкости. Коукли и Найборг [15] используют термин «кавитация» при описании активности — простой или сложной — пузырьков или полостей, содержащих газ или пар, в жидкости или других средах, включающих в себя жидкость.
В этом разделе под акустической кавитацией понимается образование и активизация газовых или паровых полостей (пузырьков) в среде, подвергаемой ультразвуковому воздействию.
По общепринятой терминологии существуют два типа активности пузырьков: стабильная кавитация и коллапсирующая, или нестационарная, кавитация, хотя граница между ними не всегда четко очерчена.
Стабильные полости пульсируют под воздействием давления ультразвукового поля (см. рис. 12.6). Радиус пузырька колеблется около равновесного значения, полость существует в течение значительного числа периодов звукового поля.
Рис. 12.6. Зависимость радиуса кавитационных пузырьков от времени в ультразвуковом поле: а—стабильная кавитация: полости существуют в течение значительного количества периодов звукового поля, осцилляции происходят вокруг равновесного радиуса; б—коллапсирующая (нестационарная) кавитация: полости осциллируют неустойчиво, растут быстро, схлопываются энергично. Р—действующее звуковое давление, R — радиус пузырька, t — время.
С активностью такой стабильной кавитации может быть связано возникновение акустических микропотоков и высоких сдвиговых напряжений.
Коллапсирующие или нестационарные полости осциллируют неустойчиво около своих равновесных размеров, вырастают в несколько раз и энергично схлопываются. Их активность проявляется в течение нескольких периодов звукового поля. Схлопыванием таких пузырьков могут быть обусловлены высокие температуры и давления, а также преобразование энергии ультразвука в излучение света или химические реакции.
Происхождение пузырьков, растущих и проявляющих активность под действием приложенного акустического поля, всегда было предметом дискуссии.
Большие пузырьки радиусом R будут всплывать в жидкости со скоростью, определяемой стоксовой силой вязкого сопротивления и выталкивающей силой:

где ![]() — плотность жидкости,
— плотность жидкости, ![]() —вязкость жидкости. Пузырек радиусом 10 мкм, например, всплывает со скоростью ~0,2 мм/с. Более мелкие пузырьки могут растворяться. Рассмотрим пузырек радиусом R, давление внутри которого обозначим через pъ. Если р — гидростатическое давление в жидкости, то разность давлений на границе пузырька равна
—вязкость жидкости. Пузырек радиусом 10 мкм, например, всплывает со скоростью ~0,2 мм/с. Более мелкие пузырьки могут растворяться. Рассмотрим пузырек радиусом R, давление внутри которого обозначим через pъ. Если р — гидростатическое давление в жидкости, то разность давлений на границе пузырька равна
![]()
где ![]() — коэффициент поверхностного натяжения. Как следует из приведенного выражения, с уменьшением радиуса пузырька избыточное давление внутри него увеличивается. Для пузырьков радиусом 1 мкм в жидкости, для которой
— коэффициент поверхностного натяжения. Как следует из приведенного выражения, с уменьшением радиуса пузырька избыточное давление внутри него увеличивается. Для пузырьков радиусом 1 мкм в жидкости, для которой ![]() = 80 дн/см, избыточное давление достигает 1,5 атм.
= 80 дн/см, избыточное давление достигает 1,5 атм.
Для ненасыщенной жидкости давление растворенного газа ръ меньше гидростатического давления р. Из этого следует, что давление внутри пузырька больше давления газа в жидкости (pъ > рg) и газ будет диффундировать из полости. Следовательно, малые пузырьки в жидкости будут растворяться. Можно рассчитать [33], что в воде, насыщенной газом (рg =pъ), пузырек радиусом 10 мкм растворится за 7 с.
Поскольку большие пузырьки всплывают под действием выталкивающей силы, а маленькие растворяются, необходимо как-то объяснить существование зародышей, из которых образуются полости. Было предложено несколько гипотез стабилизации газовых или паровых зародышей.
Сетте и Вандерлинг [125] сообщали, что космические лучи, нейтроны и тяжелые ионы могут создавать зародыши кавитации в такой жидкости как вода. В работе [50] описывается образование зародышей кавитации нейтронами и альфа-частицами.
Фокс и Герцфельд [39] выдвинули предположение, что органические молекулы могут формировать оболочку пузырька, которая будет препятствовать диффузии газа из него. Другая теория, выдвинутая Флинном [38] для объяснения стабилизации микропузырьков, предполагает, что на поверхности пузырька накапливается электрический заряд.
На пылинках и примесных частицах, содержащихся в жидкостях, а также на поверхности сосуда могут существовать микротрещины. Эти микротрещины, также как и твердые частицы, могут служить ловушками для газа. Апфель [1] обсуждал роль частичек примесей в возникновении кавитации. Избыточное давление внутри частичек, задаваемое ![]() /R, где R — радиус частичек, мало, но под действием звука достаточно высокой интенсивности газ может накачиваться в них и полости могут расти. Было показано, что интенсивность звука, необходимая для получения кавитации, заметно повышается при увеличении чистоты жидкости.
/R, где R — радиус частичек, мало, но под действием звука достаточно высокой интенсивности газ может накачиваться в них и полости могут расти. Было показано, что интенсивность звука, необходимая для получения кавитации, заметно повышается при увеличении чистоты жидкости.
Малые пузырьки могут расти вследствие процесса, называемого выпрямленной, или направленной, диффузией. Простое объяснение этого явления состоит в том, что за период акустического поля газ поочередно диффундирует в пузырек во время фазы разрежения и из пузырька во время фазы сжатия. Так как поверхность пузырька в фазе разрежения максимальна, суммарный поток газа направлен внутрь пузырька, поэтому пузырек растет. Более детальное объяснение дано Ши и Плессетом в работе [67]. Чтобы пузырек рос за счет выпрямленной диффузии, амплитуда акустического давления должна превысить пороговое значение. Порог выпрямленной диффузии, как полагают, и определяет порог кавитации.
Основные моменты ловли сома в конце осени.Как признано в современных публикациях, акустическая кавитация имеет несколько порогов (см. рис. 12.8). Неппирас [100, 101] определяет два порога, а именно порог стабильной кавитации и порог нестационарной кавитации. В [90] сообщается, что выше порога нестационарной кавитации существует еще один порог, при превышении которого кавитация вновь приобретает стационарный характер.
Пороги обычно задаются параметрами: РA — амплитудой акустического давления, Р0 — внешним давлением, R0 — начальным радиусом пузырька и ![]() — круговой частотой ультразвука.
— круговой частотой ультразвука.
12.2.3.1. Порог стабильной кавитации
Ши и Плессет [67] показали, что скорость газового потока, направленного внутрь пузырька в фазе разряжения, dm/dt, дается выражением
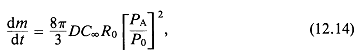
где D — коэффициент диффузии, ![]() — концентрация газа в жидкости в отсутствие пузырька. При этом пренебрегалось влиянием поверхностного натяжения. Для его учета необходимо умножить правую часть на величину [101].
— концентрация газа в жидкости в отсутствие пузырька. При этом пренебрегалось влиянием поверхностного натяжения. Для его учета необходимо умножить правую часть на величину [101].
Скорость, с которой газ диффундирует из пузырька в фазе сжатия, равна
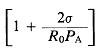
где Со — концентрация газа в насыщенной жидкости.
Пороговая величина достигается тогда, когда потоки газа в обеих фазах периода изменения давления равны, откуда следует, что
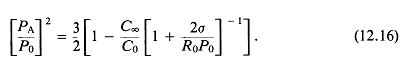
При превышении порога пузырьки могут расти и в конечном счете достигать резонансных размеров в звуковом поле. Уравнение (12.16) применимо для пузырьков, размеры которых много меньше резонансных.
Неппирасом [101] показано, что порог более точно определяется выражением
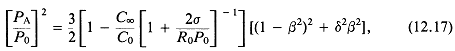
где
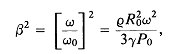
![]() — коэффициент затухания,
— коэффициент затухания, ![]() ,
, ![]() — вынужденная и резонансная угловые частоты соответственно [15].
— вынужденная и резонансная угловые частоты соответственно [15].
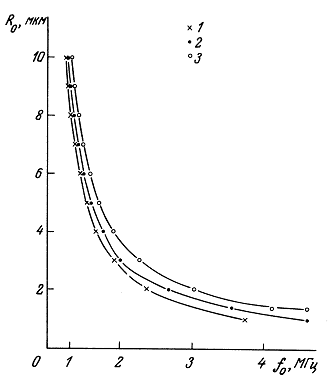
Рис. 12.7. Зависимость резонансных радиусов пузырьков от частоты. Условия расчета:
1) ![]() = 0,
= 0, ![]() =1;
=1;
2) ![]() = 7,3 Н/м2,
= 7,3 Н/м2, ![]() =1;
=1;
3) ![]() = 7,3 Н/м2,
= 7,3 Н/м2, ![]() = 1,4.
= 1,4.
При выводе уравнения (12.17) принималось во внимание, что пузырек в жидкости является резонансной системой. Для частот ниже 100 кГц резонансная частота определяется выражением [89]:
![]()
где ![]() —показатель адиабаты газа внутри пузырька.
—показатель адиабаты газа внутри пузырька.
Выше 100 кГц следует учитывать влияние поверхностного натяжения, и резонанс определяется тогда по формуле
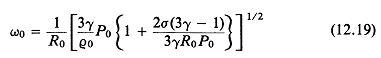
(ср. уравнение (4.31)).
В мегагерцевом диапазоне частот эффективная величина ![]() лежит между 1 и 1,4. На рис. 12.7 приведены графики зависимости резонансных размеров пузырьков от частоты при различных значениях коэффициента поверхностного натяжения и показателя адиабаты [15]. Из уравнения (12.17) следует, что амплитуда акустического давления, необходимая для возбуждения кавитации, достигает минимума на резонансной частоте.
лежит между 1 и 1,4. На рис. 12.7 приведены графики зависимости резонансных размеров пузырьков от частоты при различных значениях коэффициента поверхностного натяжения и показателя адиабаты [15]. Из уравнения (12.17) следует, что амплитуда акустического давления, необходимая для возбуждения кавитации, достигает минимума на резонансной частоте.
12.2.3.2. Пороги коллапсирующей кавитации
Верхние и нижние значения порога, определяющие интервал акустических давлений, выше которого возникает коллапсирующая или нестационарная кавитация, вычислены, например, в работах [101 103, 104].
Для малых пузырьков, размеры которых существенно ниже резонансного, порог нестационарной кавитации известен как порог Блейка [7]. Он дается выражением [101]
![]()
Для пузырьков, размеры которых больше резонансного, выражение преобразуется следующим образом:
![]()
где Rr—резонансный радиус, ![]() .
.
12.2.3.3. Кавитационные процессы в безграничной жидкости
Можно описать процесс кавитации в свободной от границ жидкости с помощью диаграмм «давление—радиус», как показано на рис. 12.8. Кривая А соответствует порогу стабильной кавитации в соответствии с уравнением (12.17), кривая В—порогу Блейка в соответствии с уравнением (12.20), и кривая С—порогу, определяемому уравнением (12.21).
Рис. 12.8. Схематическая диаграмма, показывающая пороги нестационарной кавитации В, С и порог выпрямленной диффузии A. Р—амплитуда акустического давления, R — радиус пузырьков.
Любой пузырек в области I будет растворяться в жидкости. Пузырек в области 11(a) сначала растет нестабильным образом, затем коллапсирует и, возможно, распадается на микропузырьки различных размеров, которые пополняют области II и III. Пузырьки в области II могут расти вследствие выпрямленной диффузии, устойчиво пульсируя. Некоторые пузырьки в процессе роста попадают в область III, где они коллапсируют, другие (Ь) будут оставаться в области II до тех пор, пока не вырастут до размера, при котором они всплывут и выйдут из поля. Этот процесс известен как дегазация.
Таким образом, если в среде появляются зародыши кавитации, то далее образование пузырьков с размерами, подходящими для проявления ими кавитационной активности в ультразвуковом поле, становится самоподдерживающимся процессом.
Существует несколько методов, пригодных для контроля активности кавитации в жидкости. Они делятся на три основных класса, а именно измерение акустического излучения от кавитирующей среды, анализ химических реакций, инициируемых в среде, и прямое наблюдение пузырьков. Обсуждение здесь ограничено методами, пригодными для контроля кавитации в биологических системах.
12.2.4.1. Акустическое излучение
Кавитационные пузырьки действуют как вторичные источники звука, излучение которых можно контролировать и анализировать. Гидрофон в окрестности кавитационной области может принимать акустические сигналы, которые затем подаются на спектроанализатор или частотные фильтры, чтобы выделить характерные частоты. При низких, подпороговых интенсивностях принимается сигнал только основной частоты f0. При увеличении интенсивности спектр акустического излучения от среды становится более сложным.
Субгармоника f0/2. Эше [34] впервые описал излучение субгармоники f0/2 от кавитационных пузырьков. Сейчас это стало общепринятым индикатором активности пузырьков. Механизм излуче ния субгармоники широко обсуждался, но до сих пор не понят до конца [13, 31, 73, 97 — 100, 129].
Нерегулярное излучение субгармоники обнаруживается и при стабильной кавитации. В работе [100] обсуждался возможный механизм этого явления. Частота колебаний поверхности пузырька может оказаться равной половине вынуждающей частоты, но слабая связь этих колебаний с жидкостью означает, что они могут регистрироваться только датчиком, находящимся на поверхности пузырька. Пузырьки, размеры которых равны резонансному на частоте субгармоники, могут излучать сигнал на своей собственной частоте. Неппирас [97] показал, что пороговая интенсивность при этом будет ниже порога нестационарной кавитации. При некоторых условиях в сильно сжимаемой, нелинейной жидкости сигнал частоты f0/2 может быть обнаружен вследствие параметрического излучения и в отсутствие кавитации [128], но маловероятно, чтобы он достиг заметной величины на фоне кавитационных пузырьков.
Как только интенсивность ультразвука превышает порог нестационарной кавитации, амплитуда субгармонического сигнала стремительно возрастает. При таких интенсивностях субгармоника может излучаться пузырьками, у которых время жизни до схлопыва-ния длится два периода акустического поля. Амплитуда субгармонического сигнала достигает плато при увеличении интенсивности звукового пучка (см. рис. 12.9, а).
Мортон с соавт. [93] показали, что степень биологических повреждений в клетках, облученных in vitro, хорошо коррелирует с полной энергией субгармоники, принимаемой от образцов во время облучения ультразвуком. Это один из очень немногочисленных примеров, демонстрирующих, что акустическая величина может количественно предсказать биологические изменения.
Другие гармоники. При стабильной кавитации наиболее заметна вторая гармоника (2f0). Также наблюдаются ультрагармоники частот (2n + 1) f0/2.
При достижении и превышении порога нестационарной кавитации уровень принимаемых субгармоник и высших гармоник возрастает. Вторая гармоника остается наибольшей из них, но также становится заметной ультрагармоника Зf0/2. Неппирас и Коукли [102] предположили, что ее появление может быть обусловлено взаимодействием между сигналом основной частоты f0 и субгармоникой f0/2. В работах [100, 102] также отмечено появление субгармоники f0/З. Вероятно, механизм ее излучения тот же, что и механизм субгармоники f0/2.
Рис. 12.9а. Зависимость уровня кавитации от интенсивности ультразвука для дегазированной и недегазированной воды. Показаны амплитуда субгармонической компоненты и выход иода [64]. I — Амплитуда субгармоники: I —дегазированная вода, 2— недегазированная вода; II—выход иода.
Рис. 12.96. Зависимость акустического излучения кавитационной области от тока возбуждения излучателя при исследовании в свежезалитой, насыщенной воздухом воде [99]. Показаны амплитуды основного тона, субгармоники и белого шума.
Белый шум. При возникновении кавитационной активности в ультразвуковом поле уровень белого шума, т. е. сигнала с непрерывным спектром в широкой полосе частот, возрастает. При достижении порога нестационарной кавитации уровень белого шума стремительно увеличивается и при дальнейшем увеличении интенсивности растет пропорционально амплитуде давления ультразвука, возбуждающего кавитацию [100] (см. рис. 12.9, б).
Баргер [3] обнаружил, что белый шум возникает при возбуждении поверхности пузырька. Неппирас и Коукли [102] также нашли, что белый шум излучается благодаря возмущениям, связанным с быстрыми перемещениями пузырьков в акустическом поле высокой интенсивности. Ударные волны, излучаемые захлопывающимися пузырьками при нестационарной кавитации, тоже вносят свой вклад в уровень шума.
За исключением случая субгармоники f0/2, до сих пор не показана количественная связь между шумоизлучением и специфическими биологическими эффектами.
Рис. 12.9в. Влияние интенсивности ультразвука на амплитуду субгармоники и повреждение клеток: 1 — неповрежденные клетки; 2 — неразрушенные клетки (по пробе трипановым синим); 3 — выжившие клетки (эксперимент с клонированием). Видна корреляция между уровнем субгармоники и разрушением клеток [93].
12.2.4.2. Изменение импеданса
При образовании пузырьков в облучаемой жидкости изменяется и ее акустический импеданс, что может служить мерой активности кавитации. Акустический импеданс среды, в которой распространяется звук, можно определить, измеряя изменение электрического сигнала на преобразователе [102]. Это чувствительный метод контроля активности кавитации, исключающий возмущения ультразвукового поля введением какого-либо датчика. В высокоинтенсивном поле импеданс воды может уменьшаться по крайней мере на 60% [118]. При этом напряжение на выходе преобразователя становится частотно модулированным. Характерные частоты могут быть определены путем использования соответствующих фильтров. Характер наблюдаемого гармонического и субгармонического сигнала подобен описанному в предыдущем разд. 12.2.4.
12.2.4.3. Сонолюминесценция
Явление сонолюминесценции состоит в излучении света средой, облучаемой ультразвуком и, как полагают, может служить индикатором активности нестационарной кавитации, хотя механизм свечения до сих пор до конца не понят.
Образование вуали на фотопластинках под. воз действием ультразвука впервые описали Маринеску и Триллат [81] в 1933г., а объяснение, что это явление обусловлено свечением жидкости, вызванным ультразвуком (сонолюминесценцией), предложили в 1934г. Френцель и Шультес [40].
Первые работы по сонолюминесценции состояли в прямом наблюдении световых вспышек после адаптации зрения к темноте. В водопроводной воде люминесценция еле различима, но может быть усилена при добавлении четыреххлористого углерода и насыщении воды инертными газами. В более поздних работах использовались чувствительные фотоумножители. Установлены следующие свойства сонолюминесценции:
1) сонолюминесценция уменьшается при увеличении частоты ультразвука и не наблюдается на частотах выше 2 МГц [37];
2) сонолюминесценция возникает при определенной пороговой интенсивности ультразвука и далее возрастает приблизительно пропорционально увеличивающейся интенсивности [51, 111], но может исчезнуть полностью при достижении достаточно высокой интенсивности [96];
3) сонолюминесценция уменьшается при увеличении внешнего давления [61, 113];
4) сонолюминесценция уменьшается при возрастании температуры среды.
Ранние теории объясняли возбуждение сонолюминесценции разрывом сплошности жидкости. Более поздние теории согласуются с представлением о росте пузырьков из зародышей, находящихся в жидкости. Обзор этих теорий выполнен Финчем [37]. Возникновение сонолюминесценции объясняется электрическими явлениями (см., например, [24]) или тепловым механизмом. В работах Нол-тингка и Неппираса [103, 104] предложена гипотеза, в соответствии с которой свечение объясняется возникновением равновесного теплового излучения из-за высоких температур и давлений, развивающихся при адиабатическом схлопывании пузырьков. Тот факт, что большинство свойств сонолюминесценции, описанных выше, могут быть объяснены этой моделью, а излучение света происходит в той фазе пульсаций пузырька, когда его объем минимален [96], делают эту гипотезу правдоподобной. Гриффинг и Сетте [51] предложили термохимический механизм, основанный на предположении, что возникает тепловая диссоциация молекул, а затем их рекомбинация, сопровождающаяся вместо теплового излучения хемилюминесцен-цией. Термохимический механизм требует меньше энергии, чем тепловой, и согласуется с экспериментами по обнаружению люминесценции в режиме стабильной кавитации, когда отсутствуют какие-либо возмущения на поверхности пульсирующих пузырьков [120].
Сонолюминесценция является полезным методом изучения физики нестационарной кавитации в жидкостях, но неприменима для исследования кавитации в тканях. Это недостаток многих методик по исследованию кавитации.
12.2.4.4. Звукохимия
Еще одним индикатором кавитационной активности в облученном образце является возникновение химических реакций, типичных для среды с компонентами, обогащенными энергией. К ним относятся ионизированные и возбужденные молекулы, ионы, свободные радикалы. Как полагают, ультразвуковые химические реакции характеризуют именно нестационарную кавитацию и обусловлены электрическими и тепловыми эффектами, упомянутыми в разд. 12.2.4.3. Хотя полного понимания химических процессов еще нет, считается установленным, что под воздействием кавитации в воде идет следующая реакция [130]:
H2O ![]() Н + ОН.
Н + ОН.
Для оценки кавитационной активности обычно используют два химических следствия этой реакции, а именно:
1. Выделение свободного иода из иодида калия. Полагают, что это обусловлено действием радикала ОН. При добавлении четырех-хлористого углерода выделение иода увеличивается из-за окисляющего действия хлора [131]. Концентрация иода определяется титрованием тиосульфатом натрия с использованием крахмала в качестве индикатора.
2. Окисление сульфата железа (II) до сульфата железа (III), как это используется в методе Фрике при дозиметрии ионизирующего излучения. В упрощенном виде реакция идет следующим образом [41]:
Fe2+ + OH![]() Fe3+ + ОН—,
Fe3+ + ОН—,
Н + O2 ![]() HO2
HO2
Fe2+ + HO2![]() Fe3+ + НO2—
Fe3+ + НO2—
НO2—+ H+ ![]() H2O2,
H2O2,
Fe2+ + H2O2 ![]() Fe3+ + ОН + ОН—.
Fe3+ + ОН + ОН—.
В работе [127] было предложено применить этот метод к действию ультразвука. Выход сульфата железа (III) измерялся спектрофото-метрически. Для оценки активности кавитации можно также использовать восстановление сульфата железа (III) до сульфата железа (И).
Про звукохимические реакции можно сказать, что они полезны при изучении нестационарной кавитации in vitro, но бесполезны при экспериментах in vivo.
12.2.4.5. Методы прямого наблюдения
Визуальные наблюдения. Визуальные наблюдения пузырьков были самым первым методом изучения кавитационных явлений. До появления высокоскоростной фотографии, могли быть зарегистрированы только образование пузырьков и волновые возмущения их поверхности. Нестационарная кавитация изучалась только по таким ее физическим проявлениям, как образование микропузырьков. Нестационарные явления характеризуются временем жизни всего в несколько периодов поля (10—50 мкс), и поэтому для фиксации их на пленке необходима прецизионная методика высокоскоростного фотографирования.
Блейк [7], работая на частоте 60 кГц, при наблюдении пузырьков выделил два типа их нестационарного поведения, которые он назвал газовым и паровым. Газовые нестационарности формировались отдельными пузырьками в фокальной области, тогда как паровые нестационарности, которые возникают при более высоких интенсивностях, формируют длинные «тяжи» и при их коллапсе возникает характерный щелкающий шум. Есть некоторая путаница в литературе при использовании терминов газовая и паровая кавитация. Более принято в настоящее время использовать их для описания содержимого пузырьков [38, 100].
Уиллард [133] использовал киносъемку со скоростью 24—10000 кадров в секунду для того, чтобы показать, как нестационарные полости при захлопывании разваливаются, образуя облако микропузырьков.
Лаутерборн с соавт. использовали высокоскоростную фотографию и импульсную лазерную голографию для изучения поведения как одиночных, изолированных пузырьков [74], так и скоплений пузырьков [75]. В работах [6, 21, 75] приведены результаты киносъемки процесса образования микроструек при схлопывании полостей вблизи границ.
В большинстве вышеупомянутых работ использовались сравнительно низкие акустические частоты, когда резонансные размеры пузырьков достаточно большие, и они поддаются визуализации. На мегагерцевых частотах визуальное обнаружение становится затруднительным и практически возможно только для пузырьков, выросших до размеров значительно больше резонансных.
Ультразвуковая визуализация. Оптическое обнаружение пузырьков является полезным методом при исследовании кавитации в оптически прозрачных жидкостях, но его нереально использовать в непрозрачных средах, таких как биологические ткани.
Образование пузырька в тканях может быть проконтролировано при использовании эхо-импульсных ультразвуковых систем визуализации. Эти системы впервые были применены при изучении кессонной болезни [119] и позднее в работе [23]. Тер Хаар и Даниелс [54, 55] описали использование визуализирующей системы на частоте 8 МГц для обнаружения пузырьков, образующихся при воздействии ультразвука терапевтических интенсивностей на ткани млекопитающих. Минимальный диаметр газовых микропузырьков, обнаруживаемых этой системой, был 10 мкм. Более полно этот метод обсуждается в разд. 12.5.2.
12.2.4.6. Сравнение различных методов контроля кавитации
В табл. 12.2 сделана попытка сравнить между собой различные методы контроля кавитации, которые обсуждались в разд. 12.2.4.1 — 12.2.4.5, и указать их чувствительность при определении кавитационной активности. Все описанные методы характеризуются высокой чувствительностью при возникновении нестационарной кавитации, в то время как для стабильной кавитации пригодны только методы измерения субгармоники и высших гармоник основной частоты.
В табл. 12.3 описаны возможности применения различных методов при изучении биологических эффектов.
Было сделано несколько попыток сравнения различных методов контроля с помощью одной и той же измерительной установки. Некоторые из этих работ будут рассмотрены ниже.
Де Сантис [121] показал, что при работе в диапазоне 1—4 МГц субгармоника f0/2 обнаруживается как раз перед визуальным появлением пузырьков. Неппирас [97] наблюдал точно такое явление. Неппирас [97] в экспериментах на частоте 28 кГц и Неппирас и Коукли [102] в экспериментах с фокусированным ультразвуком частотой 1МГц продемонстрировали, что визуальное обнаружение пузырьков и возникновение белого шума происходят одновременно.
Иствуд и Ватма [28] нашли, что спорадические всплески излучения субгармоники f0/2, обнаруживаемые перед возникновением сонолюминесценции, достигают постоянного уровня, когда превышается порог ее возникновения. Широкополосный шум возникает только при наличии сонолюминесценции. Саксена и Найборг [120] показали, что пороги возникновения сонолюминесценции и белого шума совпадают, но наблюдаются редкие световые вспышки в области стабильной кавитации на частоте 30 кГц.
Грехем с соавт. [49] нашли, что на частоте 1,5 МГц выделение иода из иодида калия в присутствии тетрахлорида углерода, а также сонолюминесценция всегда сопровождались излучением субгармоники f0/2. Пороговые интенсивности ультразвука для всех трех явлений фактически совпадают. На частоте 1 МГц выделение иода, как показали Коукли и Сандерс [16], происходит при той же интенсивности, которая требуется для заметного изменения импеданса жидкости, регистрируемого по измерениям электрических параметров преобразователя. Как отмечено в [62], хотя порог появления субгармоники f0/2 и выделения свободного иода совпадают, максимальная концентрация сульфата железа (III) достигается при более высокой интенсивности.
Хилл и Кларк с соавт. [65] исследовали излучение субгармоники f0/2, выделение свободного иода, разрушение молекул ДНК до 50% от их первоначальной молекулярной массы и возникновение сонолюминесценции в водных растворах, облученных ультразвуком частотой 1 МГц. Хотя сонолюминесценция и не была обнаружена, пороговые интенсивности для других трех эффектов оказались идентичными.
Таблица 12.2. Чувствительность различных методов контроля кавитационной активности
|
Диапазон акустических давлений |
Белый шум |
Гармоники f0 |
Субгармоника f0/2 |
Другие субгармоники f0/n |
Изменение импеданса |
Сонолю- минесценция |
Звукохимия |
Прямое наблюдение, визуальные наблюдения при В-сканировании |
|
Нестационарная кавитация |
Сильный |
Да, 2f0 и 3f0/2 [102] |
Большая |
Да |
Да |
Да |
Да |
Да, можно видеть образование микропузырьков |
|
Пороговый уровень |
Уровень растет [2, 34, 100] |
Общее увеличение уровня |
Стремительный рост уровня [34] |
Растут [34, 96] |
- |
Возникает |
Да | |
|
Стабильная кавитация |
Имеется на низком уровне [100] |
Да, 2f0 большая [13, 34, 96, 100] |
Случайные появления [2, 13, 34, 96, 100, 102] |
Иногда заметны, в основном при большом f0 |
Да [13, 102] |
Нет |
Таблица 12.3. Применимость различных методов контроля кавитации для исследования биоэффектов
|
Метод |
Применимость для экспериментов in vivo |
Преимущества |
Ограничения |
|
Акустическое |
Да |
1. Чувствительный |
Непригоден для |
|
излучение |
|
индикатор кавитацион- |
больших объемов |
|
|
|
ной активности. |
тканей — излученные |
|
|
|
2. Возможность |
сигналы затухают |
|
|
|
количественных |
|
|
|
|
измерений |
|
|
Изменение |
Нет |
Чувствительный |
|
|
импеданса |
|
индикатор кави- |
|
|
|
|
тационной актив- |
|
|
|
|
ности |
|
|
Сонолюминес- |
Нет |
Возможность ко- |
Непригоден для |
|
ценция |
|
личественных |
непрозрачных |
|
|
|
измерений |
сред |
|
Звукохимия |
Нет |
Возможность коли- |
Нежелательные |
|
|
|
чественных измерений |
химические реак- |
|
|
|
|
ции могут |
|
|
|
|
ограничить ис- |
|
|
|
|
пользование в |
|
|
|
|
биологических |
|
|
|
|
образцах |
|
Оптические |
Нет |
Дает информацию о |
1. Непригоден |
|
изображения |
|
местоположении пу- |
для непрозрачных |
|
|
|
зырьков |
сред |
|
|
|
|
2. Непригоден |
|
|
|
|
для высоких |
|
|
|
|
частот |
|
|
|
|
( |
|
Ультразвуковые |
Да |
1. Дает информацию |
1. Обнаруживает |
|
изображения |
|
о местоположении |
только существо- |
|
|
|
пузырьков. |
вание пузырьков, |
|
|
|
2. Исследования |
но не дает |
|
|
|
могут вестись при |
информации об |
|
|
|
повышенных давле- |
их активности |
|
|
|
ниях |
2. Существующие |
|
|
|
|
системы ограничены размерами пузырьков > 10 мкм |
12.2.5. ЭКСПЕРИМЕНТАЛЬНО ИЗМЕРЕННЫЕ ПОРОГИ КАВИТАЦИИ
Интенсивность ультразвука, при которой возникает акустическая кавитация в исследуемом образце, зависит от чистоты образца, его газосодержания, предыстории воздействия на него ультразвуком и внешним давлением, вязкости, температуры и давления среды, частоты ультразвука и режима импульсного воздействия, а также конфигурации ультразвукового поля в образце. Поэтому бессмысленно приводить величины порогов кавитации без детального рассмотрения условий, при которых они измерялись. Как указывает Коукли [14], величины для кавитационных порогов в воде на частоте 1 МГц, судя по публикациям, могут изменяться от 1 до 2,7•103 Вт/см2.
12.2.5.1. Влияние интенсивности ультразвука на твитационную активность
Пока интенсивность ультразвука, воздействующего на исследуемый объем, очень мала, нет никаких признаков кавитации. Она начинается, когда интенсивность ультразвука превысит пороговый уровень. Если при дальнейшем увеличении интенсивности оказывается превышен порог нестационарной кавитации, кавитационная активность возрастает. Уровень кавитационной активности достигает плато и может даже уменьшиться при дальнейшем увеличении интенсивности ультразвука.
На рис. 12.9а приведены полученные Хиллом [64] данные, демонстрирующие зависимость уровня субгармоники и выхода свободного иода от среднего уровня интенсивности ультразвука частотой 1 МГц как в дегазированной, так и в недегазированной воде. Неппирас [99] исследовал, как возрастают уровни субгармоники и белого шума при увеличении интенсивности (рис. 12.96).
На рис. 12.9в показаны данные из работы Мортона и соавт. [93], в которой суспензия клеток облучалась ультразвуком частотой 1 МГц и контроль осуществлялся по уровню субгармоники. Полная энергия субгармоники, излученная в течение 30-минутного воздействия, определялась интегрированием сигнала. Было показано, что существует четко выраженная пороговая интенсивность, при которой возникает излучение субгармоники. При превышении этого же порога начинается лизис клеток, наблюдается повреждение их мембран (подтверждаемое прокрашиванием трипановым синим); кроме того, оставшиеся целыми клетки начинают терять способность размножения, что подтверждается экспериментом с клонированием [59].
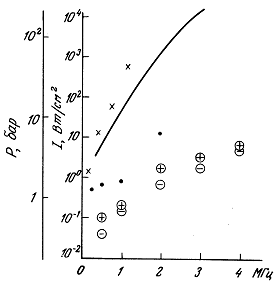
Рис. 12.10. Частотная зависимость кавитационного порога в воде с равновесной концентрацией растворенного воздуха. Собраны данные из различных источников [64].
12.2.5.2. Влияние частоты ультразвука на порог кавитации
Хилл [64] собрал литературные данные по влиянию частоты ультразвука на кавитацию. Из этих данных в целом следует, что при увеличении частоты ультразвука требуется более высокая интенсивность для возбуждения кавитации (рис. 12.10).
12.2.5.3. Влияние импульсных режимов на кавитационную активность
Хилл и Йоши [66] при использовании импульсного режима воздействия показали, что выделение свободного иода из водного раствора возрастает, а затем уменьшается при увеличении коэффициента заполнения импульса от 0,01 до 1 при длительности импульсов в интервале от 0,03 мс до 10 мс и частоте ультразвука 2 МГц. Максимум скорости выхода свободного иона наблюдается при коэффициенте заполнения от 10 до 30%. Эти данные приведены на рис. 12.11, а. На рис. 12.11, б показаны данные той же работы [66] по влиянию длительности импульсов ультразвука на скорость выделения свободного иода. Как видно из графика, максимальная скорость выделения свободного иода наблюдается при длительности импульса 10 мс (при коэффициенте заполнения 0,1). Полагают, что эти факты объясняются пульсациями пузырьков резонансных или близких к ним размеров.
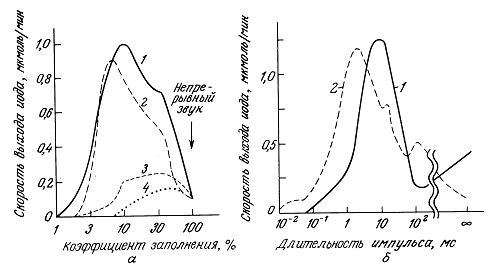
Рис. 12.11. а — Зависимость уровня кавитации (по скорости выхода иода) от коэффициента заполнения импульса. Длительность импульса: 7) 10 мс; 2) 1 мс, 3) 0,1 мс, 4) 0,03 мс; б—зависимость уровня кавитации от длительности импульса: ![]() — частота 1 МГц, средняя по пространству интенсивность в импульсе 2,2 Вт/см2; 2 —частота 2 МГц, интенсивность 4,7 Вт/см2 [66].
— частота 1 МГц, средняя по пространству интенсивность в импульсе 2,2 Вт/см2; 2 —частота 2 МГц, интенсивность 4,7 Вт/см2 [66].
12.2.5.4. Влияние внешнего давления на порог кавитации
Хилл [64] показал, что порог кавитации в газонасыщенной воде возрастает при увеличении внешнего давления (рис. 12.12а). Подобная связь была отмечена Галловеем [42].
Мортон с соавт. [94] продемонстрировали влияние внешнего давления на потерю клетками суспензии репродуктивной способности под действием кавитации при частоте ультразвука 1 МГц (рис. 12.9в). На рис. 12.126 показано, как повышение внешнего давления на 0,5—3 атм влияет на величину пороговой интенсивности, при которой происходит гибель клеток. При атмосферном давлении этот порог равен 0,1 Вт/см2, а при повышении давления на 0,5 атм — 2 Вт/см2. При избыточном давлении 2 атм клетки выживают при интенсивности ультразвука вплоть до 3 Вт/см2.
12.2.5.5. Влияние газосодержания облучаемой среды на порог кавитации
Страсберг [126] показал, что амплитуда акустического давления, требуемая для возбуждения кавитации, падает при увеличении газосодержания облучаемой жидкости (рис. 12.13).
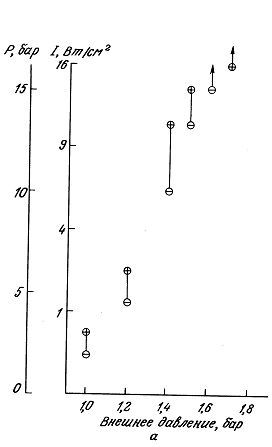
Рис. 12.12а. Зависимость порога кавитации от внешнего давления, частота 1 МГц, непрерывное излучение [64].
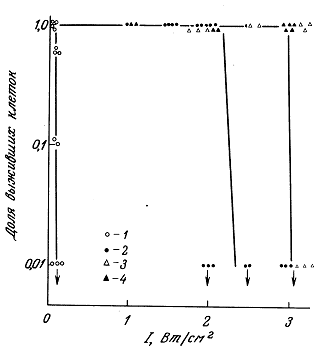
Рис. 12.126. Влияние внешнего давления на пороговые интенсивности ультразвука для повреждения клеток (эксперимент с клонированием). Внешнее давление: /) атмосферное, 2) 1,5 бара, 3) 3 бара, 4) 4 бара. Частота 1 МГц, экспозиция 30 мин [94]
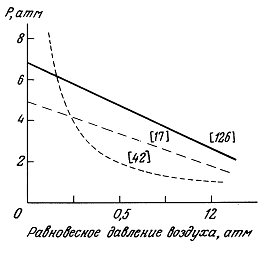
Рис. 12.13. Влияние концентрации растворенного воздуха в воде на порог кавитации [124].
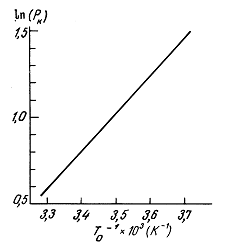
Рис. 12.14. Влияние абсолютной температуры на порог кавитации Рк [17].
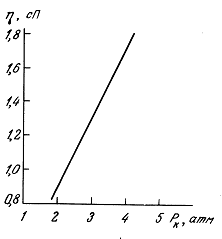
Рис. 12.15. Влияние вязкости жидкости на порог кавитации [17].
12.2.5.6. Влияние температуры среды на порог кавитации
Конноли и Фокс обнаружили [17], что существует линейная связь между ln(Рк) и величиной, обратной абсолютной температуре среды, где Рк — порог кавитации (рис. 12.14). Рк падает при увеличении температуры. Хотя существует очень мало опубликованных данных по влиянию температуры на кавитацию, та же самая тенденция отмечена несколькими экспериментаторами.
12.2.5.7. Влияние вязкости среды на порог кавитации
Порог кавитации растет с увеличением вязкости. Бриггс с соавт. [8] обнаружили линейную связь между ln(![]() ) и пороговой амплитудой акустического давления, тогда как Конноли и Фокс [17] показали, что связь между вязкостью и акустическим давлением почти линейна (рис. 12.15).
) и пороговой амплитудой акустического давления, тогда как Конноли и Фокс [17] показали, что связь между вязкостью и акустическим давлением почти линейна (рис. 12.15).
12.3. РАДИАЦИОННОЕ ДАВЛЕНИЕ, АКУСТИЧЕСКИЕ ТЕЧЕНИЯ И ДРУГИЕ НЕТЕПЛОВЫЕ МЕХАНИЗМЫ
Физические механизмы воздействия ультразвука на ткани, описанные в разд. 12.1 и 12.2, а именно тепловые и кавитационные, хорошо исследованы и в настоящее время ни у кого нет сомнений в том, что они вызывают изменения в биологических системах.
В этом разделе мы обсудим класс явлений нетепловых и некави-тационных но своей природе, но тем не менее таких, которые могут вызывать биоэффекты. Факты биологического действия этих явлений, как будет видно, менее достоверны, чем для тепла и кавитации, и во многих случаях вместо доказательств существуют лишь гипотезы. В последующих главах этой книги будет доказано, что такие нетепловые и некавитационные механизмы воздействия ультразвука могут иметь большое значение для терапевтического и хирургического применения ультразвука или выявления вредных побочных воздействий, которые могут вызываться при этом.
Ультразвук оказывает силовое воздействие на стенки сосуда, в котором распространяется, а также на любую неоднородность, попадающую в поле. Эти силы имеют две компоненты — осциллирующую, имеющую частоту ультразвука и среднее по времени значение, равное нулю, и компоненту с ненулевым средним значением. Эта постоянная компонента носит название радиационной силы и возникает из-за нелинейности процессов распространения звука. Этот предмет уже рассматривался теоретически в этой книге (см. разд. 1.8).
Радиационная сила может использоваться для определения средних интенсивностей путем измерения отклонений мишени под действием ультразвукового пучка (см. разд. 1.3 и 3.4). Можно показать, что сила, действующая на идеально отражающую мишень, Равна
![]()
где S — площадь поперечного сечения мишени [109].
Сила, действующая на идеально поглощающую мишень, равна
![]()
Радиационная сила, действующая на сферу радиусом ![]() в плоской ультразвуковой волне, может быть записана (уравнение (3.36)) как
в плоской ультразвуковой волне, может быть записана (уравнение (3.36)) как
![]()
где Yp — константа.
Подобным образом может быть получено выражение для радиационной силы, действующей на твердую сферу, малую по сравнению с длиной волны (![]() ). Общее выражение для силы, действующей на такую сферу в ультразвуковом поле, которое симметрично в ближайшей окрестности такой сферы, следующее:
). Общее выражение для силы, действующей на такую сферу в ультразвуковом поле, которое симметрично в ближайшей окрестности такой сферы, следующее:
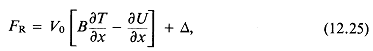
где К0 — объем сферы, Т и U — средние по времени плотности кинетической энергии (T) и потенциальной энергии (U), вычисленные во втором приближении, ![]() , где
, где ![]() — плотность сферы.
— плотность сферы. ![]() — слагаемое, которое важно только в случае, когда Т и U существенно однородны, как, например, в плоской бегущей волне [106].
— слагаемое, которое важно только в случае, когда Т и U существенно однородны, как, например, в плоской бегущей волне [106].
Можно показать, что в поле стоячих волн, уравнение (12.25) упрощается [57]:

Можно также вычислить силу, действующую на сжимаемую сферу [47, 140]. Показано, что сила, действующая на сжимаемую сферу, равна сумме силы, действующей на твердую сферу, и силы, обусловленной ее сжимаемостью [20]. Эллер [30] показал, что сила, обусловленная сжимаемостью сферы, Fc, равна
![]()
где ![]() обозначает усреднение по времени, V(t) — мгновенный объем сферы, р(х, t) — распределение давления вдоль оси х.
обозначает усреднение по времени, V(t) — мгновенный объем сферы, р(х, t) — распределение давления вдоль оси х.
Сила, действующая на сжимаемую сферу из-за радиационного давления в поле стоячих волн, Fsw, равна [52]
![]()
где
![]()
Пространственный период этой силы равен половине длины волны и, таким образом, она может быть ответственна за явление стаза клеток крови [27, 58], при котором циркулирующие в небольших кровеносных сосудах эритроциты под действием поля стоячих звуковых волн собираются в хорошо заметные плоские скопления, ориентированные нормально к направлению поля.
Направление, в котором частички движутся в стоячей волне, зависит от знака функции ![]() [140]. При стазе клеток крови сгустки эритроцитов образуются в узлах давлений [48].
[140]. При стазе клеток крови сгустки эритроцитов образуются в узлах давлений [48].
Акустическое течение — это однонаправленная циркуляция, которая может возникать при воздействии акустического поля на текучую среду. Градиенты скорости, связанные с таким движением среды, могут быть достаточно большими особенно в окрестности границ раздела, попадающих в поле. Сдвиговые напряжения, возникающие при этом, могут вызывать изменения или повреждения в тканях.
Если известны мгновенные значения давления, плотности и скорости в некоторой точке однородной изотропной среды р(х, у, z, t), ![]() (x, у, z, t) и
(x, у, z, t) и ![]() (x, у, z, t) соответственно, то уравнение движения записывается так:
(x, у, z, t) соответственно, то уравнение движения записывается так:
![]()
или
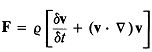
где F — суммарная сила, действующая на единичный объем вследствие напряжений в среде. Для текучей среды с объемной вязкостью ![]() и сдвиговой вязкостью г] можно показать [72], что
и сдвиговой вязкостью г] можно показать [72], что
![]()
Найборг [105] использовал уравнение (12.30) для получения общего уравнения течений
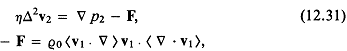
где v1 — скорость в первом порядке приближения, v2 и р2 — соответственно скорость и давление во втором порядке приближения.
Можно показать [105], что средний во времени вращающий момент, действующий на элемент среды из-за вязких напряжений, связанных с v2, равен ![]() , где
, где ![]() — момент инерции сферического элемента объема.
— момент инерции сферического элемента объема.
Таким образом, элемент среды в нелинейном звуковом поле подвержен действию как перемещающей силы, так и вращающего момента. Вращающий момент максимален в области поля, в которой максимален градиент скорости, например на границе двух различных сред. Джексон и Найборг [70] подтвердили это экспериментально, наблюдая в ультразвуковом поле за движением полистироловых сфер в смеси воды с глицерином.
Акустические течения вызывают значительные напряжения на границах раздела в жидкости из-за возникающих там градиентов скорости (см. разд. 12.3.3). Возникновением течений могут объясняться увеличение теплопередачи, ускорение различных процессов и срыв клеточных оболочек, которые происходят в биологических тканях в результате воздействия ультразвука (более детально см. в разд. 12.4 и 12.5).
Поскольку скорости однонаправленных циркуляций среды в ультразвуковом поле пространственно неоднородны, в среде возникают градиенты скорости. Объекты, попадающие в такие течения, подвергаются действию сдвиговых напряжений. Градиенты скорости максимальны вблизи границ, поскольку отсутствие проскальзывания определяет нулевую скорость среды на границе. Область, в которой скорость изменяется от нуля до ее значения в объеме среды, называется пограничным слоем. Его толщина может быть выражена как
![]()
где ![]() — круговая частота звукового поля,
— круговая частота звукового поля, ![]() и
и ![]() — плотность и сдвиговая вязкость среды соответственно [108].
— плотность и сдвиговая вязкость среды соответственно [108].
Видно, что толщина пограничного слоя обратно пропорциональна корню из частоты. Так, например, для воды на частоте 1 МГц она равна 5,6-10-5 см.
В среде возникают два типа градиентов скорости. Градиенты скорости, обусловленные акустическими течениями, стационарны и относительно постоянны во времени. Периодическая природа ультразвука приводит к тому, что в среде на границах возникают и градиенты колебательной скорости.
Сдвиговое напряжение 5, связанное с градиентом скорости G, есть
![]()
Найборг [109] рассчитал, что в воде на частоте 1 МГц и при интенсивности 1 Вт/см2 эти колебательные напряжения порядка 200 Н/м2.
Можно показать, что колебательные напряжения выражаются
как
![]()
Постоянное напряжение, возникающее на границе из-за однонаправленных течений вокруг колеблющейся сферической частицы радиусом b, равно [116]
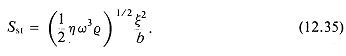
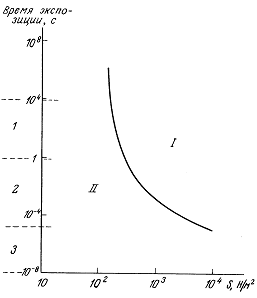
Рис. 12.16. Влияние времени экспозиции на критические сдвиговые напряжения для гемолиза красных кровяных телец. I—Область воздействия объемных напряжений; II—область воздействия поверхностных эффектов. Способы создания сдвиговых напряжений: I — вискозиметр из концентрических цилиндров; 2 — капилляры, пузырьки, осциллирующие проволочки; 3— струи [80].
Хотя постоянные напряжения могут быть на порядок меньше колебательных напряжений, они действуют на границе более длительное время и оказывают более существенное воздействие на клетки. При изучении биоэффектов, производимых сдвиговыми напряжениями, широко применяют гемолиз красных кровяных телец в суспензии in vitro (например, [80, 116]).
Вполне естественно, что критические напряжения, необходимые для гемолиза, увеличиваются при уменьшении длительности их действия. Это иллюстрирует рис. 12.16.
Высокие сдвиговые напряжения в акустических течениях, могут, таким образом, быть причиной повреждений в биологических тканях. Предполагают, например, что повреждения эндотелия, наблюдаемые как в кровеносных сосудах эмбрионов цыплят [27], так и в кровеносных сосудах матки мышей [58], обусловлены частично сдвиговыми напряжениями, возникающими из-за акустических течений. Это предположение основано на том, что повреждение имеет место на облученной стороне стенки сосуда, где жидкость контактирует с оболочкой. На внешней стороне стенки тоже имеется жидкость, но более вязкая, чем плазма крови и, таким образом, вязкие напряжения, возникающие из-за акустических течений, здесь будут менее значительными.
12.3.4. АКУСТИЧЕСКИЕ МИКРОПОТОКИ ВОКРУГ ПУЗЫРЬКА
Осцилляции пузырьков в звуковом поле вызывают неоднородные движения жидкости в непосредственной близости от пузырька. Из-за малого масштаба таких течений их называют микротечениями или микропотоками. Образующиеся высокие градиенты скоростей могут вызывать значительные сдвиговые напряжения на границах раздела, попадающих в зону таких микропотоков. Это может быть еще одним механизмом повреждающего действия кавитацион-ного поля.
Элдер [29] описал картину микропотоков вокруг пузырька, возникающую при различных амплитудах осцилляций пузырьков и коэффициентах вязкости жидкости при условии, что пузырек находится на какой-либо поверхности. Характер пограничных слоев и вихрей, возникающих вокруг пузырьков, показан на рис. 12.17.
Микропотоки в цитоплазме наблюдались при возбуждении газовых включений в листьях растений под воздействием ультразвука [82, 85].
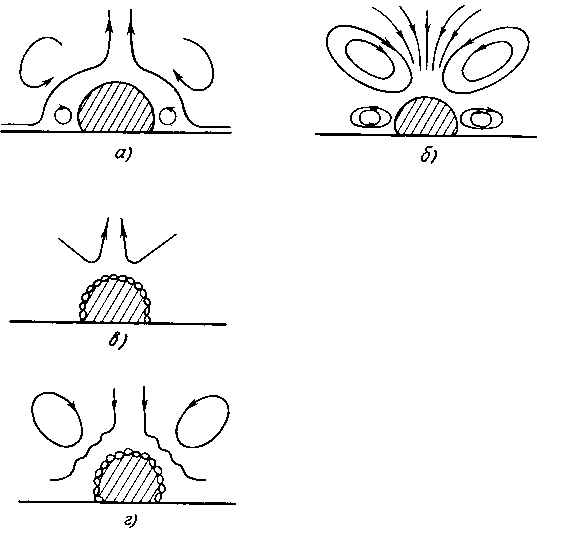
Рис. 12.17. Четыре режима акустических течений. Пузырек возбуждается поверхностью, на которой он находится, а — Поверхность сплющивает пузырек, низкоамплитудные осцилляции в жидкости с малой вязкостью; б—то же, что для а, но для более широкого диапазона амплитуд и вязкостей; в и г — при возбуждении поверхностных мод колебаний пузырька (в возникает при разрушении моды б; г возникает, когда разрушается стабильная поверхностная мода и течение возвращается к моде б) [29].
Биомакромолекулы и клетки в окрестности пузырьков будут подвергаться действию сдвиговых напряжений, возникающих из-за микропотоков (см. разд. 12.3.3). Руни [115] показал, что эти напряжения могут приводить к гемолизу, если амплитуда пульсаций превышает пороговую величину.
Градиент скорости G вокруг колеблющегося пузырька радиусом Ro связан с толщиной пограничного слоя ![]() следующим образом:
следующим образом:
![]()
где ![]() — амплитуда колебаний пузырька. Таким образом, сдвиговое напряжение равно [108, 109]
— амплитуда колебаний пузырька. Таким образом, сдвиговое напряжение равно [108, 109]
![]() .
.
12.3.5. ДРУГИЕ НЕТЕПЛОВЫЕ ЭФФЕКТЫ
На объект в ультразвуковом поле действует много различных сил, обусловленных вязкостью жидкости.
Сила, препятствующая перемещению сферического тела радиуса а со скоростью ![]() в среде с вязкостью
в среде с вязкостью ![]() , известная как стоксова сила сопротивления, дается выражением
, известная как стоксова сила сопротивления, дается выражением
![]()
Для диска это выражение домножается на постоянный коэффициент К:
![]()
Если диск движется плоскостью вперед, К = 0,85, если ребром, то К = 0,57 [71]. Если в жидкости есть градиент скорости, то на диск будет действовать и вращающий момент.
Может возникать сила, обусловленная зависимостью вязкости от температуры. При распространении звука температура среды меняется в разных фазах цикла изменения давления. Соответствующие изменения вязкости приводят к возникновению усредненной по времени силы. Для идеальных жидкостей результирующая сила, вероятно, пренебрежимо мала, поскольку вязкость обратно пропорциональна корню квадратному из абсолютной температуры. Однако для сложных сред, таких как биологические ткани, в которых может существовать сильная температурная зависимость вязкости, эта сила может оказаться весьма значительной.
Рост температуры среды вызывает увеличение скорости звука. Это означает, что распространение волн конечной амплитуды становится нелинейным и гребень звуковой волны движется быстрее впадины, что приводит к искажению формы волны (ср. разд. 1.8). Синусоидальная волна может, таким образом, превратиться в пилообразную. Скорость изменения импульса частицы будет больше, когда она находится в фазе нарастания давления в волне, чем в фазе его убывания, и силы, действующие на частицу в этих фазах, будут различными. Результирующая сила, известная как сила Озеена, зависит от амплитуды второй гармоники волны [132] и, как правило, пренебрежимо мала для воды, но может быть значительной для тканей (см. разд. 2.7). При распространении пилообразной волны высокочастотные компоненты затухают быстрее, и форма волны возвращается к синусоидальной.
12.3.6. СИЛЫ ВЗАИМОДЕЙСТВИЯ ЧАСТИЦ
Если две частицы расположены близко друг к другу в ультразвуковом поле, то между ними возникает сила взаимодействия, обусловленная воздействием на колеблющуюся частицу звука, переизлученного другой частицей.
Эмблтон [32] рассмотрел взаимодействие двух сфер, когда линия, соединяющая их центры, параллельна направлению распространения плоской бегущей волны. В этом случае сила пропорциональна произведению объемов сфер и увеличивается при уменьшении расстояния между ними.
Гершой и Найборг [44] развили эту теорию и рассмотрели взаимодействие двух сфер, линия центров которых расположена под произвольным углом д к направлению распространения волны. Было показано, что возникают сила отталкивания вдоль направления распространения и сила притяжения в перпендикулярном направлении. В итоге сила описывается следующим образом:
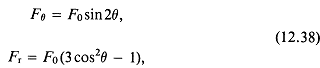 ,
,
где
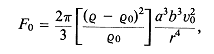
Биофизика ультразвуковых эффектов 477
а и b — радиусы сфер, r — их удаление друг от друга, v0 — амплитуда скорости окружающей среды, до — плотность. Для касающихся друг друга эритроцитов в плазме крови максимальная сила равна 10-13 Н при 1 Вт/см2, 3 МГц, а = b = 4 мкм, ![]() = 1,1/1,03.
= 1,1/1,03.
Радиационные силы, обусловленные газовыми пузырьками. Если газовый пузырек попадет в озвучиваемую жидкость, он будет осциллировать под действием ультразвука и как вторичный источник взаимодействовать с частицами вокруг себя. Будет возникать сила притяжения к пузырьку, точно такая же, как описанная выше сила взаимодействия частиц. Поскольку для пузырька в воде или плазме крови ![]() , сила может быть записана следующим образом (см. уравнение
, сила может быть записана следующим образом (см. уравнение
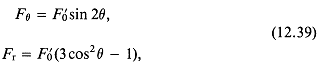 ,
,
где
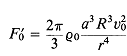
Миллер с соавт. [88] показали, что если тромбоциты облучать ультразвуком в присутствии газовых пузырьков, стабилизированных в порах фильтровальной бумаги, то уже при малой интенсивности SPTA 32 мВт/см2 тромбоциты собираются в сгустки около пузырьков.
Если пузырьки размером меньше резонансного, то в поле стоячих волн они движутся по направлению к пучности давления [22].
Если скорость границы пузырька радиуса R равна ![]() , то скорость среды v1 в точке
, то скорость среды v1 в точке ![]() на расстоянии d равна
на расстоянии d равна
![]()
Сила, действующая на сферу объемом Vo в точке Q, равна
![]()
где
![]()
Таким образом,
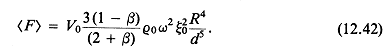
Можно показать [57], что
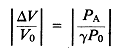 ,
,
где ![]() V — изменение объема под действием волны давления амплитуды Ра при внешнем давлении Р0. Под воздействием ультразвука частотой 3 МГц и интенсивностью 1 Вт/см2 сфера радиусом 4 мкм притягивается к пузырьку радиусом 1 мкм с силой 10-9 Н, когда они касаются друг друга, и с силой 10-14 Н, когда они удалены друг от друга на 10 мкм. Роль такой силы в ускорении образования сгустков красных кровяных телец при осцилляции пузырьков в поле стоячих волн описана в работе [57].
V — изменение объема под действием волны давления амплитуды Ра при внешнем давлении Р0. Под воздействием ультразвука частотой 3 МГц и интенсивностью 1 Вт/см2 сфера радиусом 4 мкм притягивается к пузырьку радиусом 1 мкм с силой 10-9 Н, когда они касаются друг друга, и с силой 10-14 Н, когда они удалены друг от друга на 10 мкм. Роль такой силы в ускорении образования сгустков красных кровяных телец при осцилляции пузырьков в поле стоячих волн описана в работе [57].
Рассмотрим три возможных типа биологических структур и оценим, какие из обсуждавшихся выше сил наиболее важны в каждом случае.
1. Жидкость, заключенная в определенные границы, например кровь в кровеносном сосуде, цитоплазма в растительной клетке.
Когда жидкость течет вдоль фиксированной границы, устанавливается градиент скорости, вызывающий сдвиговые напряжения. Если интенсивность ультразвука достигает определенного уровня, в объеме жидкости возникают акустические течения, что увеличивает градиент скорости и, следовательно, сдвиговые напряжения.
2. Структуры, зафиксированные своим окружением, например лизосомы, митохондрии.
Структура, которая имеет плотность, отличную от окружающей ее среды, подвергается воздействию периодических перемещающих сил, равных для сферических объектов произведению их объема на разность плотностей и на ускорение.
Большинство структурных включений в биологических системах имеют ту же плотность, что и их окружение, поэтому эффект будет малым. Объект, помещенный в жидкость и прикрепленный к границе раздела жидкость — твердое тело, подвергается действию сдви
говых напряжений и даже может двигаться в жидкости, если связь с границей не жесткая.
3. Объекты, способные свободно перемещаться в жидкости, например эритроциты, тромбоциты, пузырьки.
Объект, находящийся в поле и имеющий акустический импеданс, отличный от импеданса окружающих ее тканей, может двигаться за счет радиационного давления и, что наиболее вероятно, притягиваться к границе. Точно так же возникающая в окрестности пузырька сила будет притягивать объект к пузырьку.
12.4. НЕКАВИТАЦИОННЫЕ ИСТОЧНИКИ СДВИГОВЫХ НАПРЯЖЕНИЙ
Для изучения влияния акустических течений и связанных с ними сдвиговых напряжений и градиентов скоростей, подобных тем, что возникают вокруг стабильных осциллирующих пузырьков, было сконструировано несколько различных аппликаторов, предназначенных для создания вибраций в локальных точках. Наиболее часто для этих целей применяются колеблющаяся игла или проволочка.
Дайер и Найборг [25, ПО] использовали тонкую проволочку с острием размером до 5—20 мкм, возбуждаемую продольно на частоте около 25 кГц, для изучения акустических течений в растительных клетках. Проволочка прижимается к внешней стороне клеточной стенки. При различных амплитудах вибраций наблюдаются разные эффекты. В одном из экспериментов [26] было найдено, что при амплитудах вибраций 1—2 мкм наблюдаются слабые, но четко определенные движения в цитоплазме, при амплитудах 3—5 мкм наблюдаются упорядоченные и довольно быстрые потоки, а при амплитудах выше 5 мкм — хаотические быстрые движения, которые приводят к разрушениям клеток. Подобные эффекты наблюдаются, когда острие проволочки расположено не далее 10 мкм от клеточных стенок.
Качественно сходные результаты получили Вильсон с соавт. [138], возбуждая акустические течения в зародышевых клетках морских беспозвоночных. В этом эксперименте облучение ультразвуком частотой 85 кГц проводилось с помощью ступенчатого экспоненциального преобразователя. Дайер и Найборг [26] обсудили биофизику эффектов, возникающих при использовании этих устройств. Приведены описания вихрей, наблюдаемых в жидкости, а также скопление частиц и их вращение (см. разд. 12.5).
Вильяме с соавт. [134, 136] использовали поперечно колеблющуюся проволочку (диаметр 115 мкм, частота 20 кГц) для определения сдвиговых напряжений, достаточных для гемолиза красных кровяных телец в суспензии. Было установлено, что пороговое значение составляло 560 Н/м2, что соответствовало амплитуде вибраций 20 мкм. Когда такая проволочка, вибрирующая с амплитудой более 10 мкм, касалась кровеносного сосуда in vivo, в нем возникало скопление тромбоцитов [135]. При амплитудах в интервале 5—8 мкм иногда наблюдались тромбоциты, прилипшие к эндотелиальной поверхности сосуда. В работе [19] использовалась подобная система для исследования воздействия на лейкоциты в плазме крови собаки. Показано, что пороговые сдвиговые напряжения для разрушения лейкоцитов ниже, чем для эритроцитов.
Хотя колеблющиеся иглы и проволочки представляют собой хорошую модель осцилляций стабильных пузырьков, было бы еще более полезно использовать реальные пузырьки. Главной проблемой является стабилизация резонансных пузырьков в ультразвуковом поле. Руни [115] преодолел эту проблему путем стабилизации полусферического пузырька на конце трубки диаметром 260 мкм, возбуждаемой на частоте 20 кГц. Было показано, что пороговое напряжение для гемолиза эритроцитов в суспензии составляет приблизительно 4500 дн/см2 или 450 Н/м2. Это хорошо согласуется с результатом работы Вильямса [134], полученным с помощью колеблющейся проволочки.
Притчард с соавт. [114] исследовали повреждения ДНК в растворе. Макромолекулы облучались с помощью пластины, возбуждаемой на частоте 20 кГц, в которой были насверлены отверстия диаметром 200 мкм, что приблизительно равно диаметру резонансных воздушных пузырьков в воде на этой частоте. На отверстиях происходила стабилизация осциллирующих пузырьков, вызывающих повреждение ДНК.
Была также исследована активность пузырьков в мегагерцевом диапазоне частот. Миллер с соавт. [88] описали систему, в которой фильтр с гидрофобным покрытием и отверстиями диаметром от 0,1 до 10 мкм облучался в суспензии клеток. В работе [87] эти же исследователи так описывают движение тромбоцитов:
«1. Частицы вблизи отверстия движутся к нему, скорость этого движения нарастает тем быстрее, чем ближе частица к центру. Часто наблюдаются небольшие агрегаты частиц вблизи отверстий после кратковременного непрерывного облучения. Движение тромбоцитов обусловлено действием радиационного давления.
2. Частицы вблизи отверстия увлекаются акустическим течением, подобно тому, как это происходит вблизи газовых пузырьков в низкочастотном поле. Когда биологический объект, например тромбоцит, вовлекается в такое движение, он может подвергнуться воздействию относительно высоких напряжений и получить повреждения, если попадет в область пограничного слоя вблизи отверстия.
3. Частицы или клетки, собиравшиеся вблизи отверстия, могут плавно вращаться или двигаться нерегулярным образом. Если частицы не очень симметричны, как, например, эритроциты, имеющие форму диска, то у них возникает определенная ориентация, которую они стремятся сохранить. Если несколько эритроцитов собирается около одного и того же отверстия, то они взаимодействуют сложным образом, демонстрируя интересные сочетания вращений и ориентацию).
Эти авторы сделали вывод, что пороговая интенсивность для агрегации тромбоцитов лежит в интервале 32—64 мВт/см2 на частоте 1 МГц. Вильяме и Миллер [137] продемонстрировали выделение АТФ (наводящее на мысль о повреждении мембран) из эритроцитов, облученных ультразвуком с пиковой по пространству интенсивностью 20—30 мВт/см2 (SPTA) на частоте 1,6 МГц.
Такие эксперименты показывают, что существование стабильных осциллирующих пузырьков может приводить в некоторых случаях к повреждению и разрушению биологических структур подобно тому, как это происходит при кавитации в объеме жидкости. Исследования биологических эффектов в подобных искусственных условиях позволяет вычленить конкретные механизмы действия, которые нельзя было изучать в более сложной системе.
С теоретической точки зрения весьма интересно выявить факты резонансного усиления эффективности воздействия ультразвука на отдельных частотах основного тона или его модуляции. Такие публикации редки, но имеется интересное сообщение Сарвазяна с соавт. [122], в котором сообщается об эффектах повреждения эмбрионов амфибий явно нетепловой и некавитационной природы, причем эффекты были максимальны при частотах повторения импульсов 10—20 и ПО—130 Гц соответственно для двух различных препаратов.
12.5. НАБЛЮДЕНИЯ ЭФФЕКТОВ НЕТЕПЛОВОЙ ПРИРОДЫ В СТРУКТУРИРОВАННЫХ ТКАНЯХ
Основные усилия в изучении эффектов нетепловой природы были нацелены на исследование кавитации. Имевшиеся до недавнего времени методы исследования кавитации непригодны для изучения непрозрачных тканевых структур (см. разд. 12.2.4, табл. 12.2, 12.3). По этой причине в большинстве опубликованных работ по кавитации в тканях эксперименты проводились на растительных тканях, в которых возможны прямые оптические наблюдения. Кроме того, выполнялись косвенные оценки на основе гистологических исследований тканей млекопитающих; образцы тканей извлекались и фиксировались после воздействия ультразвуком.
Чрезвычайно трудно достоверно разделить эффекты, вызванные нетермическими и некавитационными механизмами, поскольку трудно выделить эти эффекты при наличии кавитации или нагрева. Однако есть несколько работ такого рода; они описаны в разд. 12.5.2.
Некоторые биологические аспекты действия ультразвука на саморегулирующиеся биологические системы обсуждались Сарвазя-ном [123].
Одна из наиболее ранних работ по нетепловому действию ультразвука была выполнена Гарвеем [60]. В ней сообщалось о разрушении клеточных стенок, скручивании и отрыве от них органелл, движении в цитоплазме в Spirogyra, Nitella и Elodea. Эти эффекты уменьшались, если перед облучением снижалось содержание газа в растениях. Хотя автор не наблюдал газовых пузырьков, по-видимому, эти эффекты были обусловлены акустическими течениями и кавитацией.
Миллер [84] выделил три вида реакции листьев Elodea, которые, как известно, содержат естественные газовые вакуоли, на ультразвуковое воздействие, а именно: слабые возмущения (удлинение цикла развития, изменения в распределении хлоропластов), разрушения клеточной организации, приводящие к ее гибели, и гомогенизация содержимого клеток. Он установил, что реакция клеток на воздействие ультразвуком частотой 1 МГц очень неоднородна в каждом листе, поскольку чувствительность каждой клетки зависит от ее близости к газовому включению. Широкие исследования в области пороговых интенсивностей показали, что интенсивность ультразвука (SPTP), приводящая к гибели клеток, обратно пропорциональна времени облучения в степени 0,29. Миллер [85, 86] обнаружил, что пиковые по пространству пороговые интенсивности, приводящие к гибели клеток, очень сильно зависят от частоты ультразвука.
Гершой с соавт. [43] показали, что возмущения в клетках вблизи межклеточных газовых включений возникают при средней интенсивности 350 мВт/см2 (1 МГц), хотя в некоторых клетках вращения хлоропластов и вихревые течения обнаруживались при 35 мВт/см2. Необратимые эффекты не наблюдались при интенсивности ниже 3,5 Вт/см2. В растениях, таких как Hydrodictyon, устранение межклеточных газовых включений приводило к повышению пороговых интенсивностей для слабых возмущений до 35 Вт/см2 п-> равнению с 350 мВт/см2 в корнях Vicia faba, которые содержат TdivHe включения. В работе [46] изучалось влияние стоячих волн на растения. Было показано, что максимальные разрушения, вызванные ультразвуком, наблюдались в пучностях давления как в Spirogyra, так и в Elodea. Наблюдаемые эффекты авторы связали с активностью пузырьков в ткани листьев.
Моррис и Коукли [91, 92] измеряли излучение субгармоники в процессе облучения ультразвуком корней растений. Удалось показать, что на частоте 1 МГц появление субгармоники и замедление роста корней Vicia faba наблюдается при одной и той же интенсивности. Субгармоника была зарегистрирована при интенсивности 24 Вт/см2 после облучения в течение 70 с. Быстрое повышение температуры корней предшествовало значительному росту излучения субгармоники. Карстенсен с соавт. [9] обнаружили такое же замедление роста корней горошка Pisum sativum.
12.5.2.1. Кавитационные явления
Очень трудно получить однозначное доказательство возникновения кавитационных явлений в тканях млекопитающих. Большинство публикаций опирается на результаты гистологического анализа образцов ткани, изолированных и исследованных после облучения ультразвуком.
На гистологических срезах были обнаружены полости и отверстия, происхождение которых связывается с кавитационными пузырьками [4, 68, 76].
Леман и Херрик [76] наблюдали кровотечения на внутрибрюш-ной поверхности у мышей. При воздействии ультразвуком на частоте 1 МГц было найдено, что увеличение внешнего давления уменьшает кровотечение. Для предотвращения кровотечения при интенсивности 2,5 Вт/см2 необходимо давление 3—4 атм., при 3,5 Вт/см2 необходимо 4—5 атм. Гистологические исследования облученных тканей показывают большие пустоты, которые предположительно соответствуют газовым пузырькам.
Хаг и Пейп [68] провели гистологические исследования тканей мышей и крыс после облучения ультразвуком частотой 1 МГц. Были отмечены группы пузырьков в печени, образующиеся после воздействия ультразвуком интенсивностью 2,2 Вт/см2 в течение 8 мин. Обнаружено, что эти пузырьки образуют слой вдоль границы между белым и серым веществом мозга.
Такие образования пузырьков определяются авторами как псевдокавитация. Чрезвычайно сложно доказать, что круглые отверстия, наблюдаемые на срезах тканей при проведении гистологических исследований, действительно обусловлены пузырьками, существовавшими в момент фиксации срезов. В работе Белла [4] также сообщалось о псевдокавитационных отверстиях в печени мышей. Было показано, что повреждения наблюдались на частоте 1 МГц, но их не было на частоте 27 МГц. Хотя повреждения напоминали те, что возникают из-за перегрева тканей; предварительное охлаждение и поддержание температуры тканей на приемлемом уровне во время ультразвукового воздействия не предотвращает повреждения. Подобные полости наблюдались при исследовании в электронном микроскопе облученных тканей матки мыши [58].
Хаг и Пейп [68] провели измерения интенсивности ультразвука, прошедшего через свежеиссеченный образец тканей в зависимости от времени. Оказалось, что для некоторых типов тканей после приблизительно 120 с облучения интенсивность существенно падает. Авторы связывают это с образованием пузырьков в ткани, препятствующих распространению ультразвука через нее. Сильнее всего этот эффект проявляется в мозге и печени (см. рис. 12.18). В жире интенсивность сначала растет, а затем падает до 50% первоначальной величины. Первоначальный подъем интенсивности был связан с нагревом жира, вызывающим уменьшение коэффициента поглощения.
Мартин с соавт. [83] изучали воздействие ультразвука частотой 0,8, 1,5, 3,0 МГц на печень мышей, причем облучение велось через контактную среду. На частотах 0,8 и 1,5 МГц для интенсивностей выше 2 Вт/см2 наблюдались локализованные поверхностные повреждения на стороне печени, обращенной к источнику ультразвука. На частоте 3 МГц вплоть до интенсивности 10 Вт/см2 таких повреждений не отмечено. Измеренное повышение температуры со
Рис. 12.18. Диаграмма, показывающая падение интенсивности ультразвука, прошедшего через различные ткани, происходящее через 120 с облучения. Падение обусловлено образованием пузырьков в тканях [68]. 1 — Печень; 2 — мозг, белое вещество; 3— яичко; 4 — поджелудочная железа; 5 — селезенка; 6— мышца; 7—жир; 8—кожа; 9— почка; 10—легкое.
ставляло 7,5° С. Интенсивность ультразвука, при которой появлялись первые повреждения, совпадала с интенсивностью, при которой возникал субгармонический сигнал. Исследование показало, что наблюдаемые эффекты обусловлены кавитационными явлениями в контактной среде. Используя гель или накладывая на печень тонкую пленку, повреждения можно было предотвратить.
Тер Хаар и Даниелс [54] использовали 8-мегагерцевую ультразвуковую визуализирующую систему для наблюдения за образованием пузырьков в конечностях анестезированных морских свинок. Эта система, разработанная для изучения кессонной болезни, не позволяла получить сведения об активности образовавшихся пузырьков. При облучении ультразвуком с частотой 0,75 МГц и длительностью 5 мин пузырьки впервые были замечены при интенсивности 80 мВт/см2. При иснользовании этого метода можно обнаружить пузырьки диаметром больше 10 мкм, т. е. существенно больше резонансного размера. В более поздней работе тер Хаар с соавт. [55] продемонстрировали, что повышение внешнего давления приводит к исчезновению пузырьков. На рис. 12.19 схематически показана картина ультразвукового изображения на частоте 8 МГц перед (а) облучением и во время (б) облучения ультразвуком частотой 0,75 МГц. Некоторые из наблюдаемых пузырьков после возникновения стабильно существуют в определенной точке, другие видны в течение короткого времени. Большинство пузырьков возникает в части конечности, на которую падает пучок ультразвука; по-видимому, они локализуются около жировых прослоек и межмышечных фасций.
Рис. 12.19. Ультразвуковые изображения конечности морской свинки: а) контрольное изображение; б) изображение, показывающее новые эхо-образы, которые приписываются пузырькам внутри конечности, возникающим при ее облучении ультразвуком частотой 0,75 МГц и интенсивностью 1 Вт/см2. 1 — Местоположение зонда диагностического прибора; 2 — местоположение терапевтического излучателя.
Если считать, что каждое событие на изображении — это возникновение нового пузырька, то рис. 12.20 показывает, как меняется общее количество пузырьков со временем при различных интенсивностях для двух животных. Рис. 12.20а— 12.20в показывают, как число событий меняется при изменении внешнего давления и как оно растет с увеличением интенсивности ультразвука. Таким способом можно определить порог образования пузырьков.
Рис. 12.20а. Суммарное число событий (возникновение пузырьков в конечности морской свинки) кдк функция времени для двух разных животных при различной интенсивности ультразвука: 1) 80 мВт/см2, 2) 150 мВт/см2, 3) 300 мВт/см% 4) 680 мВт/см2 [54].
Рис. 12.206. Влияние приложенного давления на число событий. Видно, что с увеличением внешнего давления число пузырьков уменьшается [55].
Рис. 12.20в. Влияние интенсивности ультразвука на число событий. Данные взяты для четырех животных. Черточки показывают количество ложных событий, регистрируемых в контрольных опытах.
Исследования показали, что достаточно низкие, терапевтические интенсивности ультразвука (см. гл. 13) могут привести к образованию пузырьков in vivo. Однако об активности этих вновь образованных пузырьков ничего нельзя сказать. Необходима уже другая система, чтобы выяснить как ведут себя эти пузырьки в ультразвуковом поле.
12.5.2.2. Акустические течения
Белл [4] выполнил гистологические исследования тканей млекопитающих после их облучения ультразвуком частотой 1 МГц и отметил часто наблюдающиеся повреждения стенок кровеносных сосудов. Дайсон с соавт. [27] наблюдали подобные эффекты при облучении куриных эмбрионов ультразвуком частоты 3 МГц. На некоторых препаратах сосудов было видно, что повреждается облучаемая сторона плазматической мембраны. Подобные результаты получены тер Хаар с соавт. [58], которые использовали электронную микроскопию для изучения воздействия ультразвука частотой 3 МГц на матку мышей. И в этом случае повреждения были замечены на облученной стороне плазмалемм, а в просвете сосудов были видны сгруппированные в определенных местах фрагменты оболочек. Предполагается, что этот тип повреждений обусловлен высокими сдвиговыми напряжениями, связанными с акустическими течениями в плазме крови вблизи стенок кровеносных сосудов.
12.5.2.3. Стоячие волны
Гольдман и Лепешкин [46] показали, что при помещении растительных клеток в поле стоячих волн все наблюдаемые биологические эффекты были пространственно связаны с пучностями давления. Хотя проведение подобных экспериментов in vivo в тканях млекопитающих затруднительно, в некоторых работах была сделана попытка исследовать воздействие стоячих волн на кровоток. Шмитц [124] впервые продемонстрировал на лягушках, что при достаточно высокой интенсивности ультразвука эритроциты собираются в сгустки на расстоянии в половину длины волны друг от друга. Дайсон с соавт. [27] продемонстрировали тот же эффект на куриных эмбрионах в возрасте 3 Vi дня, а тер Хаар с соавт. [57, 58] на кровеносных сосудах млекопитающих. При включении звука эритроциты удерживаются в сгустке постоянно, в то время как плазма продолжает течь по сосуду. Этот эффект обычно обратимый, поскольку сгустки рассасываются после выключения звука, распределяясь параболически (в соответствии с распределением скорости течения) по сечению сосуда.
Биофизика ультразвуковых воздействий — достаточно сложная область. С точки зрения физики нетрудно перечислить возможные механизмы взаимодействий, которые возникают в биологических тканях. Труднее выявить эти механимы экспериментально, чтобы подтвердить их существование и установить пороги их возникновения. Например, интенсивности ультразвука, необходимые для возбуждения коллапсирующей кавитации, достаточны и для значительного нагрева тканей, но способов исключить взаимное влияние этих разных механизмов не существует.
Внимательный читатель, наверное, заметил отсутствие количественной информации в этой главе. Причина проста — ее нет. Данные на рисунках, насколько это было возможно, приведены в точном соответствии с экспериментальными условиями конкретного опыта. В этой ситуации основную ценность представляет описание тенденций и зависимостей эффектов от акустических параметров, таких как частота и интенсивность. Очевидна необходимость в проведении более строгих экспериментов.
В следующих главах этой книги (гл. 13 и 14) изложены достоверно установленные биологические эффекты и обсуждается их связь с терапевтическим применением ультразвука или с безопасностью его диагностического использования. Надеемся, что эта глава обеспечила хорошую основу для понимания последующих глав.
1. Apfel, R. Е. (1970) The role of impurities in cavitation — threshold determination. J. acoust. Soc. Am.b4& 1179—1186.
2. Apfel, R. E. (1980) In Ultrasonics Vol. in series Methods of Experimental Physics. Vol. ed. P. Edmonds. Series ed. L. Marton. New York, Academic Press.
3. Barger, J. E. (1964) Thresholds of acoustic cavitation, Acoustics Research Lab., Harvard Univ., Cambridge, Mass., section 57.
4. Bell, E. (1957) The action of ultrasound on the mouse liver. J. Cell & Сотр. Physiol. 50 83—103.
5. Bender, L. F., Herrick, J. E, & Krusen, E H. (1953) Temperatures produced in bone by various methods used in ultrasonic therapy. Arch. Phys. Med. Rehab. 34 424—433.
6. Benjamin, T. B. & Ellis, A. T. (1966) The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries. Phil. Trans. Roy. Soc. London. A. 260 221—240.
7. Blake, F. G. (1949) The onset of cavitation in liquids. I. Cavitation threshold sound pressures in water as a function of temperature and hydrostatic pressure. Tech. Mem. 12, Acoustics Research Lab., Dept. of Engineering, Sciences and Applied Physics. Harvard University, Cambridge, Mass.
8. Briggs, H. В., Johnson, J. В., & Mason, W. P. (1947) Properties of liquids at high sound pressure. J. acoust. Soc. Am. 19 664.
9. Carstensen, E. L., Child, S. Z., Law, W. K., Horowitz, D. R., & Miller, M. W.
(1979) Cavitation as a mechanism for the biological effects of ultrasound in plant roots. J. acoust. Soc. Am. 66 1285—1291.
10. Chan, A. K., Sigelmann, R. A., Guy, A. W., & Lehmann, J. F. (1973) Calculation by the method of finite differences of the temperature distribution in layered tissues. IEEE Trans. Biomed. Engng BME-20 86—90.
11. Clarke, P. R. (1969) Studies of the biological effects of ultrasound and of synergism between ultrasound and X-rays. PhD thesis, University of London.
12. Clarke, P. R. & Hill, C. R. (1970) Physical and chemical aspects of ultrasonic disruption of cells. J. acoust. Soc. Am. 47 649—653.
13. Coakley, W. T. (1971) Acoustical detection of single cavitation events in a focused field in water at 1 MHz. /. acoust. Soc. Am. 49. 792—801.
14. Coakley, W. T. (1978) Biophysical effects of ultrasound at therapeutic intensities. Physiotherapy 64 166—169.
15. Coakley, W. T. & Nyborg, W. L. (1978) Methods and phenomena. Eds. S. P.
Wolsky, A. W. Czanderna. Vol. 3 In Ultrasound: its application in medicine and biology Part I Ed. F. J. Fry. Elsevier Scientific Publishing Co. pp. 77—159.
16. Coakley, W. T. & Sanders, M. F. (1973) Sonochemical yields of cavitation centres at 1 MHz. J. Sound & Vib 28 73—85.
17. Connolly, W. & Fox, F. E. (1954) Ultrasonic cavitation thresholds in water. J. acoust. Soc. Am. 26 843—848.
18. Crank, J. (1967) The mathematics of diffusion. Clarendon Press, Oxford.
19. Crowell, J. A., Kusserow, В. K., & Nyborg, W. L. (1977) Functional changes in white blood cells after microsonation. Ultrasound in Med. & Biol. 3 185—190.
20. Crum, L. A. (1971) Acoustic force on a liquid droplet in an acoustic stationary wave. J. acoust. Soc. Am. 50 157—163.
21. Crum, L. A. (1979) Surface oscillations and jet development in pulsating bubbles. J. de Physique 40 C8-285.
22. Crum, L. A. & Eller, A. (1970) Motion of bubbles in a stationary sound field. /. acoust. Soc. Am. 48 181—189.
23. Daniels, S., Davies J. M., Paton, W. D. M., & Smith, E. B. (1980) The detection of gas bubbles in guinea pigs after decompression from air saturation dives using ultrasonic imaging. J. Physiol. 308, 369—383.
24. Degrois, M. & Baldo, P. (1974) A new electrical hypothesis explaning sonoluminescence, chemical actions and other effects of gaseous cavitation. Ultrasonics 12 25—28.
25. Dyer, H. J. & Nyborg, W. L. (1960a) Ultrasonically induced movements in cells and cell models. IRE Trans, on Med. Electronics ME-7 163—165.
26. Dyer, H. J. & Nyborg, W. L. (1960b) Characteristics of intracellular motion induced by ultrasound. Proc. 3rd Int. Conf Med. El. London. Illiffe 445—449.
27. Dyson, M., Pond, J. В., Woodward, B. & Broadbent, J. (1974) The production of blood cell stasis and endothelial damage in the blood vessels of chick embryos treated with ultrasound in a stationary wave field. Ultrasound in Med. and Biol. 1, 133—148.
28. Eastwood, L. M. & Watmough, D. J. (1976) Sonoluminescence, in water and in human blood plasma, generated using ultrasonic therapy equipment. Ultrasound in Med. & Biol. 2, 319—323.
29. Elder, S. A. (1959) Cavitation Microstreaming. J. acoust. Soc. Am. 31 54—64.
30. Eller, A. (1968) Force on a bubble in a standing acoustic wave J. acoust. Soc. Am. 43 170—171.
31. Eller, A. & Flynn, H. G. (1968) The generation of subharmonics of order one half by bubbles in a sound fild. J. acoust. Soc. Am. 44 368(A).
32. Embleton, T. F. W. (1962) Mutual interaction between two spheres in a plane sound field. J. acoust. Soc. Am. 34 1714—1720.
33. Epstein, P. S. & Plesset, M. S. (1950) On the stability of gas bubbles in liquid gas solutions. J. Chem. Phys. 18 1505—1509.
34. Esche, R. (1952) Untersuchung der Schwingungskavitation in Flussigkeiten. Akust. Beih. No. 4, 208.
35. Filipczynski, L. (1976) Thermal effects in soft tissues developed under the influence of focussed fields of short duration. Archives of Acoustics 1 309—322.
36. Filipczynski, L. (1977) Thermal effects in soft tissues developed under the action of ultrasonic fields of long duration. Archives of Acoustics 2 297—303.
37. Finch, R. D. (1963) Sonoluminescence. Ultrasonics 1 87—98.
38. Flynn, H. G. (1964) Physics of acoustic cavitation in liquids. In: Physical acoustics (ed. W. P. Mason) Vol. IB pp. 57—172, Academic Press, N. Y. (Имеется перевод: Флинн Г. — В кн.: Физическая акустика/Под ред. У. Мэзо-на. — М.: Мир, 1967, т. 1, ч. Б, с. 7.)
39. Fox. F. Е., Herzfield, К. F. (1954) Gas bubbles with organic skin as cavitation nuclei. J. acoust. Soc. Am. 26 984—989.
40. Frenzel, H. & Schultes, H. (1934) Lumineszenz im ultrashallbeschickten Wasser. Z. Physik. Chem. 27B 421—424.
41. Fricke, H. & Hart, E. J. (1966) Chemical dosimetry Ch. 12. in Radiation dosimetry Vol. II. Instrumentation. Ed. F. H. Attrix, W. C. Roesch. Academic Press, pp. 167—239.
42. Galloway, W. J. (1954) An experimental study of acoustically induced cavitation in liquids. J. acoust. Soc. Am. 26, 849—857.
43. Gershoy, A., Miller, D. L. & Nyborg, W. L. (1976) Intercellular gas: its role in sonated plant tissue. In: Ultrasound in medicine and biology Vol. 2. Ed. D. N. White & R. Barnes. Plenum Press, N. Y. pp. 501—510.
44. Gershoy, A. & Nyborg, W. L. (1973) Microsonation of cells under near threshold conditions. In: Ultrasonics in medicine, (eds. M. de Vlieger et al.) pp. 360—365 (Int. Congress Series No. 309, ISBN 90 219 01870; Excerpta Medica, Amsterdam 1974).
45. Gersten, J. W. (1959) Temperature rise of various tissues in the dog on exposure to ultrasound at different frequencies. Arch. Phys. Med. 40, 187—192.
46. Goldman, D. E. & Lepeschkin, W. W. (1952) Injury to living cells in standing sound waves. J. Cell. Сотр. Physiol. 40, 255—268.
47. Горькое Л. П. (1961) О силах, действующих на малую частицу в акустическом поле в идеальной жидкости. ДАН СССР 140 88—91.
48. Gould, R. К. & Coakley, W. Т. (1974) The effects of acoustic force on small particles in suspension. Proc. Symp. Finite wave effects in fluids. I. P. C. Science and Tech. Press. Lyngby, Denmark.
49. Craham, E., Hedges, M., Leeman, S., & Vaughan, P. (1980) Cavitational Bioeffects at 1.5 MHz. Ultrasonics 18 224—228.
50. Greenspan, M. & Tschiegg, С. E. (1967) Radiation-induced Acoustic Cavitation; Apparatus and some results. J. Res. of N. B. S. (Q Engineering and Instrumentation 71C 299—312.
51. Griffing, V., Sette, D. (1955) Luminescence produced as a result of intense ultrasonic waves. J. Chem. Phys. 23 503.
52. ter Haar, G. R. (1977) PhD thesis, Univ, of London. The effect of ultrasonic standing wave fields on the flow of particles, with special reference to biological media.
53. ter Haar, G. R. (1980) Temperature distributions obtainable in tissue as a result of ultrasonic irradiation. In Hyperthermia in radiation oncology ed. G. Arcangeli & F. Mauro. Masson, pp. 29—35. Proc. of 1st Meeting of European Hyperthermia group. Cambridge 1979.
54. ter Haar, G. R. & Daniels, S. (1981) Evidence for ultrasonicaliy induced cavitation in vivo. Phys. Med & Biol. 26 1145—1149.
55. ter Haar, G. R., Daniels, S., Eastaugh, К. C, & Hill, C, R., (1982) Ultrasonicaliy induced cavitation in vivo. Br. J. Cancer 45 Suppl. V, 151—155.
56. ter Haar, G. R., Hopewell, J. W. (1982) Ultrasonic heating of mammalian tissues in vivo Br. J. Cancer 45 Suppl. V, 65—67.
57. ter Haar, G. R. & Wyard, S. J. (1978) Blood cell banding in ultrasonic standing wave fioelds: A physical analysis. Ultrasound in Med. and Biol. 4 111—123.
58. ter Haar, G. R., Dyson, M., & Smith, S. P. (1979) Ultrastructural changes in the mouse uterus brought about by ultrasonic irradiation at therapeutic intensities in standing wave filds. Ultrasound in Med. & Biol. 5 167—179.
59. ter Haar, G. R., Stratford, I. J., & Hill, C. R. (1980) Ultrasonic irradiation of mammalian cells in vitro at hyperthermic temperatures. Brit. J. Radiol. 53 784—789.
60. Harvey, E. N. (1930) Biological aspects of ultrasonic waves, a general survey. Biol. Bull. 59 306—325.
61. Harvey, E. N. (1939) Sonoluminescence and sonic chemiluminescence. J. Am. Chem. Soc. 61 2392—2398.
62. Hedges, H. J., Leeman, S., & Vaughan, P. (1977) Acoustic cavitation, Proc. Underwater Acoustics Group, Inst, of Acoustics No. 5, p. 19.
63. Herrick, J. F. (1953) Temperatures produced in tissues, by ultrasound: experimental study using various techniques. J. acoust. Soc. Am. 25 12—16.
64. Hill, C. R. (1972) Ultrasonic exposure thresholds for changes in cells and tissues. J. acoust. Soc. Am. 52 667—672.
65. Hill, C. R., Clarke, P. R., Crowe, M. R., Hammick, J. W. (1969) Biophysical effects of cavitation in a 1 MHz ultrasonic beam. Proc. Conf Ultrasonics for Industry, pp. 26—30 (Iliffe, London 1969).
66. Hill, C. R. & Joshi, G. P. (1970) The significance of cavitation in interpreting the biological effects of ultrasound. Proc. Conf on Ultrasonics in Biol. & Med. UBIOMED-70 Warsaw. Polish Acad, of Sciences.
67. Hsieh, D.-Y. & Plesset, M. S. (1961) Theory of recitfied diffusion of mass into gas bubbles. /. acoust. Soc. Am. 33 206—215.
68. Hug, O. & Pape, R. (1954) Nachweis der Ultraschallkavitation in Gewebe. Strahlentherapie 94 79—99.
69. Hynynen, K., Watmough, D. J., & Mallard, J. R. (1981) The effects of some physical factors on the production of hyperthermia by ultrasound in neoplastic tissues. Radiat. Environ. Biophys. 19 215—226.
70. Jackson, F. J. & Nyborg, W. L. (1958) Small scale acoustic streaming near a locally excited membrane. I. acoust. Soc. Am. 30 614—619.
71. Lamb, H. (1945) Hydrodynamics. Dover, New York. §309. (Имеется перевод Лэмб X. Гидродинамика. — М. — Л.: Гостехиздат, 1947.)
72. Ландау, Л. Д., Лифшиц, Е. М. (1985) Гидродинамика. М., Наука.
73. Lauterborn, W. (1976) Numerical investigation of non-linear oscillations of gas bubbles in liquids. J. acoust. Soc. Am. 59 283—293.
74. Lauterborn, W. & Bolle, H. (1975) Experimental investigations of cavitaitonbubble collapse in the neighbourhood of a solid boundary. J. Fluid Mech. 72 391—399.
75. Lauterborn, W., Hinsch, K., & Bader, F. (1972) Holography of bubbles in water as a method to study cavitation bubble dynamics. Acustica 26 170—171.
76. Lehmann, J. F. & Herrick, J. F. (1953) Biologic reactions to cavitation, a consideration for ultrasonic therapy. Arch. Phys. Med. 3 86—98.
77. Lehmann, J. E, McMillan, J. A., Brunner, G. D., & Blumberg, J. B. (1959) Comparative study of the efficiency of short wave, microwave and ultrasonic diathermy in heating the hip joint. Arch. Phys. Med. Rehab. 40 510—512.
78. Lehmann, J. E, Delateur, B. J., Warren, C. G., & Stonebridge, J. B. (1967a) Heating produced by ultrasound in bone and soft tissue. Arch. Phys. Med. Rehab. 48 397—401.
79. Lehmann, J. E, Delateur, B. J., Stonebridge, J. В., & Warren, C. G. (1967b) Therapeutic temperature distribution produced by ultrasound as modified by dosage and volume of tissue exposed. Arch. Phys. Med. Rehab. 48 662—666.
80. Leverett, L. В., Heliums, J. D., Alfrey, C. P., & Lynch, E. C. (1972) Red cell damage by shear stress. Biophys. J. 12 257—273.
81. Marinesco, N. & Trillat, J. J. (1933) Action des ultrasons sur les plaques photographiques. Compt. Rend. Acad. Sci. (Paris) 196 856—860.
82. Martin, C. J. & Gemmell, H. G. (1979) A study, of ultrasonically induced pulsations of gas filled channels in Elodea. Phys. Med. & Biol. 24 600—612.
83. Martin, C. J., Gregory, D. W., & Hodgkiss, M. (1981) The effects of ultrasound in vivo on mouse liver in contact with an aqueous coupling medium. Ultrasound in Med. & Biol. 7 253—265.
84. Miller, D. L. (1977) The effects of ultrasonic activation of gas bodies in Elodea leaves during continuous and pulsed irradiation at 1 MHz. Ultrasound in Med. & Biol. 3 221—240.
85. Miller, D. L. (1979a) A cylindrical-bubble model for the response of plant-tissuegas bodies to ultrasound. J. acoust. Soc. Am. 65 1313—1321.
86. Miller, D. L. (1979b) Cell death thresholds in Elodea for 0.45—10 MHz ultrasound compared to gas-body resonance theory. Ultrasound in Med. & Biol. 5 351—357.
87. Miller, D. L., Nyborg, W. L., & Whitcomb, С. C. (1978) In vitro clumping of platelets exposed to low intensity ultrasound. In: Ultrasound in medicine eds. White & Lyons. Vol. 4. Plenum Publishing Corp. 545—553.
88. Miller, D. L., Nyborg, W. L., & Whitcomb, С. C. (1979) Platelet aggregation induced by ultrasound under specialized conditions in vitro. Science 205 505.
89. Minnaert, M. (1933) On musical air-bubbles and the sounds of running water. Phil. Mag. 16 235—248.
90. Монахов В. H. и др. (1975) К вопросу о втором пороге ультразвуковой кавитации в воде. Акуст ж. 21 432—435.
91. Morris, J. V. & Coakley, W. Т. (1978) Detection of ultrasonic cavitation emissions from insonated plant tissues. Proc. Ultrasonics International 1977, I. P. C. Business Press Ltd. pp. 206—211.
92. Morris, J. V. & Coakley, W. T. (1980) The non-thermal inhibition of growth and the detection of acoustic emissions from bean roots exposed to 1 MHz ultrasound. Ultrasound in Med. & Biol. 6 113—126.
93. Morton, К. I., ter Haar, G. R., Stratford, I. J. & Hill, C. R. (1982) The role of cavitation in the interaction of ultrasound with V79 Chinese hamster cells in vitro. Br. J. Cancer 45 147—150.
94. Morton, К. I., ter Haar, G. R., Stratford, I. J., & Hill, C. R. (1983) Subharmonic emission as an indicator of ultrasonically induced biological damage. Ultrasound in Med. & Biol. 9 629—633.
95. Nassiri, D. K., Nicholas D., & Hill, C. R. (1979) Attenuation of ultrasound in skeletal muscle. Ultrasonics 17 230—232.
96. Negeshi, K. (1961) Experimental studies on sonoluminecsence and ultrasonic cavitation. J. Phys. Soc. Japan 16 1450—1465.
97. Neppiras, E. A. (1968) Subharmonic and other low frequency emission from bubbles in sound-irradiated liquids. J. acoust. Soc. Am. 46 587—601.
98. Neppiras, E. A. (1969a) Subharmonic and other low frequency signals from sound irradiated liquids. J. Sound Vib. 10 176—186.
99. Neppiras, E. A. (1969b) Subharmonic and other low frequency emission from bubbles in sound-irradiated liquids. J. acoust. Soc. Am. 46 587—601.
100. Neppiras, E. A. (1980a) Acoustic cavitation. Physics Reports 61 # 3 May 159—251.
101. Neppiras, E. A. (1980b) Acoustic cavitation thresholds and cyclic processes. Ultrasonics 18 201—209.
102. Neppiras, E. A. & Coakley, W. T. (1976) Acoustic cavitation in a focused field in water at 1 MHz. J. Sound Vib. 45 341—373.
103. Neppiras, E. A. & Noltingk, В. E. (1951) Cavitation produced by ultrasonics: theoretical conditions for the onset of cavitation. Proc. Phys. Soc. В 64 1032—1038.
104. Noltingk, В. E., Neppiras, E. A. (1950) Cavitation produced by ultrasonics. Proc. Phys. Soc. B. 63 674—685.
105. Nyborg, W. L. (1965) Acoustic Streaming. In: Physical acoustics ed. W. P. Mason. Academic Press, Vol. IIB Ch. 11. (Имеется перевод: Ниборг В. В кн.: Физическая акустика / Под ред. У. Мэзона. — М.: Мир, 1969, т. 2, ч. Б).
106. Nyborg, W. L. (1967) Radiation pressure on a small rigid sphere. J. acoust. Soc. Am. 42 947—952.
107. Nyborg. W. L. (1975) Ultrasound. In: Intermediate bilphysical mechanics Ch.
14, Section 9. Cummings Publishing Co. California.
108. Nyborg, W. L. (1978a) Physical mechanisms for biological effects of ultrasound. HEW Publication (FGDA) 78-8062.
109. Nyborg, W. L. (1978b) In: Ultrasound: its applications in medicine and biology (ed. E J. Fry) Vol. Ill of Methods and Phenomena: Their applications in science and technology. Part I Chapter 1: Physical principles of ultrasound, pp. 1—75 Elsevier Scientific Pub. Co.
110. Nyborg, W. L. & Dyer, H. J. (1960) Ultrasonically induced motions in single plant cells. Conf. on Medical Electronics, Paris, France, June 24—27 1959. Iliffe & Sons Pub. Eng. 391—396.
111. Parke, A. V. M. & Taylor, D. (1956) The chemical action of ultralonic waves. J. Chem. Soc. 4 4442—4450.
112. Paul, W. D. & Imig, C. J. (1955) Temperature and blood flow studies after ultrasonic irradiation. Am. J. Phys. Med. 34, 370—375.
113. Полоцкий, И. Г. (1948) Ж. физ. хим. 34 №2 787.
114. Pritchard, N. J., Hughes, D. E., & Peacocke, A. R. (1966) The ultrasonic degradation of biological macromolecules under conditions of stable cavitation. I. Theory, methods and applications to deoxyribonucleic acid. Biopolymers 4 259—273.
115. Roonev, J. A. (1970) Haemolysis near an ultrasonically pulsating gas bubble. Science 169 869—871.
116. Rooney, J. A. (1972) Shear as a mechanism for sonically induced biological effects. J. acoust. Soc. Am. 52 1718—1724.
117. Rosenberger, H. (1950) Uber den Wirkungsmechanismus der Ultraschall behandlung, ins besondere bei ischias und Neuralgien. Der Chirurg. 21 404—406.
118. Розенберг, Л. Д., Сиротюк, М. Г. (1960) Акуст. ж. 6 №4 478—481.
119. Rubissow, G. J., Mackay, R. S. (1971) Ultrasonic imaging in vivo bubbles in decompression sickness. Ultrasonics 9 225—234.
120. Saksena, Т. K. & Nyborg, W. L. (1970) Sonoluminescence from stable cavitation. J. Chem. Phys. 53 1722—1734.
121. de Santis, P., Sette, D., & Wanderlingh, F. (1967) Cavitation detection: The use of subharmonics. J. acoust. Soc. Am. 42 514—516.
122. Sarvazyan, А. P., Beloussov, L. V., Petropavlovskaya, M. N. & Ostroumova Т. V. (1982) The action of low-intensity pulsed ultrasound on amphibian embrionic tissues. Ultrasound in Med. & Biol. 8 639—654.
123. Sarvazyan, A. P., (1983) Some general problems of biological action of ultrasound. IEEE Trans. SU-30 2—12.
124. Schmitz, W. (1950) Ultraschall als biologisches Forschungsmittel. Strahlentherapie 83 654—662.
125. Sette, D. & Wanderlingh, F. (1962) Nucleation by cosmic rays in ultrasonic cavitation. Phys. Rev. 125 409—417.
126. Strasberg, M. (1959) Onset of ultrasonic cavitation in tap water. J. acoust. Soc. 31 163—176.
127. Todd, J. H. (1970) Measurement of chemical activity of ultrasonic cavitation in aqueous solutions. Ultrasonics 8 234—238.
128. Tucker, D. G. (1965) The exploitation of non-linearity in underwater acoustics. J. Sound Vib. 2 429—434.
129. Vaughan, P. W. (1968) Investigation of acoustic cavitation thresholds by observation of the first subharmonic. J. Sound. Vib. 7 236—246.
130. Weissler, A. (1959) Formation of hydrogen peroxide by ultrasonic waves: free radicals. J. Am. Chem. Soc. 81 1077—1081.
131. Weissler, A., Cooper, H. W., Snyder, S. (1950) Chemical effects of ultrasonic waves: oxidation of KI solution by CCI4. /. Am. Chem. Soc. 12 1769.
132. Westervelt, P. J. (1957) Acoustic radiation pressure. J. acoust. Soc. Am. 29 26—29.
133. Willard, G. W. (1953) Ultrasonically induced cavitation in water —A step-by-step process. J. acoust. Soc. Am. 25 669—686.
134. Williams, A. R. (1971) Hydrodynamic disruption of human erythrocytes near a transversely oscillating wire. Rheol. Acta 10 67—70.
135. Williams, A. R. (1977) Intravascular mural thrombi produced by acoustic microstreaming. Ultrasound in Med. & Biol. 3 191—203.
136. Williams, A. R., Hughes, D. E., & Nyborg, W. L. (1970) Hemolysis near a transversely oscillating wire. Science 169 871—873.
137. Williams, A. R. & Miller, D. L. (1980) Photometric determination of ATP release from human erythrocytes exposed to ultrasonically activated gas-filled pores. Ultrasound in Med. & Biol. 6 251—256.
138. Wilson, W. L., Wiercinski, F. J., Nyborg, W. L. Schnitzler, R. M., & Sichel, F. J. (1966) Deformauon and motion produced in isolated living cells by localized ultrasonic vibration. J. acoust. Soc. Am. 40 1363—1370. 139. Wood, R. W. & Loomis, A. L. (1927) The physical and biological effects of high frequency sound waves of great intensity. Phil. Mag. 4 (7) 417—436.
140. Yosioka, K. & Kawasima (1955) Acoustic radiation pressure on a compressible sphere. Acustica 5 167—173.
ПРИМЕНЕНИЕ УЛЬТРАЗВУКА В ТЕРАПИИ И ХИРУРГИИ
Г. тер Хаар
Давно известно, что ультразвук, действуя на ткани, вызывает в них биологические изменения [41]. Интерес к изучению этой проблемы обусловлен, с одной стороны, естественным опасением, связанным с возможным риском применения ультразвуковых диагностических систем для визуализации, а с другой — возможностью вызвать изменения в тканях для достижения терапевтического эффекта.
По ультразвуковой терапии существует обширная литература, хотя, к сожалению, большинство работ не отличается высоким качеством и содержит мало строгой научной информации. В этой главе обсуждение ограничено работами, имеющими прочную научную основу.
Терапевтический ультразвук может быть условно разделен на ультразвук низких и высоких интенсивностей. Основная задача применения ультразвука низких интенсивностей (0,125—3,0 Вт/см2 SATA) — неповреждающий нагрев или какие-либо нетепловые эффекты, а также стимуляция и ускорение нормальных физиологических реакций при лечении повреждений. При более высоких интенсивностях (>5Вт/см2) основная цель — вызвать управляемое избирательное разрушение в тканях.
Первое направление включает в себя большинство применений ультразвука в физиотерапии и некоторые виды терапии рака, второе — ультразвуковую хирургию.
13.2. ФИЗИОЛОГИЧЕСКИЕ ОСНОВЫ УЛЬТРАЗВУКОВОЙ ТЕРАПИИ
Распределение температуры в тканях млекопитающих при ультразвуковом нагреве, уже подробно обсуждались в разд. 12.1. Управляемый нагрев глубоко расположенных тканей может дать положительный терапевтический эффект в ряде случаев. Некоторые из них будут рассмотрены в этой главе.
В основном работы, связанные с тепловыми эффектами при терапевтическом применении ультразвука, не содержат ни достоверных измерений температурных распределений, ни надежной дозиметрии, поэтому обсуждение рассматриваемых здесь эффектов но сит качественный характер.
Высокий коэффициент поглощения ультразвука в тканях с большими молекулами обусловливает заметное нагревание коллагено-содержащих тканей, на которые чаще всего и воздействуют ультразвуком при физиотератевтических процедурах.
13.2.1.1. Увеличение растяжимости коллагеносодержащих тканей
Основной фактор, который часто препятствует восстановлению мягкой ткани после ее повреждения, — это контрактура, возникающая в результате повреждения и ограничивающая нормальное движение. Слабое прогревание ткани может повысить ее эластичность. Леман с соавт. [60] сообщили, например, что при дополнительном прогревании во время растягивающих упражнений улучшается гибкость коллагеносодержащих структур. Герстен [32] показал, что ультразвуковой нагрев приводит к увеличению растяжимости сухожилий. Рубцовая ткань также может стать более эластичной под воздействием ультразвука. Специальные применения ультразвука в физиотерапии обсуждаются в разд. 13.3.
13.2.1.2. Повышение подвижности суставов
Амплитуда движений суставов в случае контрактуры может быть увеличена путем их нагрева [5]. Для нагрева сустава, окруженного значительным слоем мягких тканей, ультразвуковой способ наиболее предпочтителен, поскольку ультразвук лучше других форм диатермической энергии проникает в мышечную ткань [40, 61].
13.2.1.3. Болеутоляющее действие
Многие пациенты отмечают ослабление болей при тепловом воздействии на пораженные области. Обезболивающий эффект может быть как кратковременным, так и продолжительным. При некоторых заболеваниях применение ультразвука для уменьшения болей дает наилучшие результаты. Например, Рубин и Куитерт [79] обнаружили, что ультразвук ослабляет фантомные боли после ампутации конечностей, а также боли, вызванные образованием рубцов и невром. Механизмы болеутоляющего действия пока неясны; возможно, в них вносят вклад и нетепловые эффекты.
13.2.1.4. Изменения кровотока
При локальном нагреве ткани часто отмечаются сосудистые реакции, проявляющиеся даже на некотором расстоянии от места воздействия.
Тер Хаар и Хоупвелл [36] показали, что кровоток в мышечной ткани увеличивается в 2—3 раза при ультразвуковом прогревании до температуры 40—45° С. О подобных явлениях сообщали так же Пауль и Имиг [72]. В работе [50] изменение кровотока связывается с местным расширением сосудов. Отмечается также, что при нагреве ультразвуком или электромагнитным излучением наблюдаются сходные эффекты. Однако Абрамсон с соавт. [1] показали, что при импульсном облучении (когда тепловые эффекты невелики) также изменяется кровоток. Эти изменения сохраняются около получаса после окончания процедуры.
Местное расширение сосудов увеличивает поступление кислорода в ткань и, следовательно, улучшает условия, в которых находятся клетки. Возможно, именно этим объясняется терапевтический эффект, а также нередко наблюдаемое усиление воспалительной реакции.
Исследование микрососудистой динамики в кремастерной мышце крысы показало, что при достаточно большой интенсивности (в данном случае > 5 Вт/см2) в некоторых сосудах может наблюдаться уменьшение просвета и объемного кровотока. Возможно, это связано не с тепловыми эффектами, а с кавитацией или другими механическими явлениями [46].
13.2.1.5. Уменьшение мышечного спазма
Прогревание может уменьшить мышечный спазм. По-видимому, это обусловлено седативным (успокаивающим) действием повышения температуры на периферические нервные окончания [24]. Ультразвук также может быть использован для этой цели.
Степень физиологической реакции на прогревание зависит от большого числа факторов, включающих достигаемую температуру, время прогревания, размер прогреваемой области и скорость увеличения температуры. Ультразвук позволяет быстро нагреть строго определенную область. К анатомическим структурам, которые избирательно нагреваются ультразвуком, относятся богатые коллагеном поверхностные слои кости, надкостница, суставные мениски, синовиальная жидкость, суставные сумки, соединительные ткани, внутримышечные рубцы, мышечные волокна, оболочки сухожилий и главные нервные стволы.
В ряде случаев ультразвук может быть более эффективной формой диатермии, чем коротковолновые излучения, парафиновые аппликации и инфракрасное излучение [68].
Нетепловые механизмы, с помощью которых ультразвук может воздействовать на ткани, описаны в гл. 12. Если принимать во внимание только физиологические эффекты, то эти механизмы можно разделить на два класса: периодические и непериодические.
Периодические эффекты возникают из самой колебательной природы звукового поля и могут рассматриваться в качестве своего рода микромассажа [84], способствующего, например, рассасыванию спаек, образующихся в мягких тканях при их повреждениях.
По-видимому, главным непериодическим эффектом, приводящим к лечебному действию ультразвука, являются акустические течения (см. разд. 12.3.2). Они могут быть вызваны устойчивыми осциллирующими полостями или радиационными силами как внутри, так и вне клеток. Акустические течения могут влиять на среду около мембран, изменяя градиенты концентраций, воздействуя тем самым на диффузию ионов и молекул через мембраны.
Чепмен с соавт. [8] показали, что ультразвук in vitro может уменьшать содержание калия в некоторых клетках, хотя, возможно, это происходило из-за влияния кавитационных пузырьков. Увеличение силы сокращения матки мышей при воздействии ультразвука может объясняться изменением содержания кальция в клетках гладких мышц. Однако чрезвычайно трудно строго выделить различные нетепловые эффекты, которые могут возникать в тканях, отделить их действие от влияния простого прогрева ткани из-за поглощения звука. Вероятно, легче всего можно выделить воздействие кавитации, поскольку существует возможность повышением внешнего давления препятствовать ее развитию.
Некоторые из нетепловых эффектов ультразвука могут нанести вред, если не принять защитных мер. В облучаемом объеме, содержащем отражающие поверхности, возможно образование стоячей волны (см. разд. 12.3.7), и эритроциты в кровеносных сосудах, попадающих в этот объем, могут собираться в сгустки. Продолжительное воздействие ультразвука в этих условиях может привести к значительному ухудшению снабжения кислородом тканей, питаемых данными сосудами.
Множество эффектов может наблюдаться при возникновении кавитационных пузырьков в тканях. Например, вокруг стабильно пульсирующих пузырьков могут возникать микропотоки.
Ультразвук широко используется в физиотерапевтической практике. Первоначально он считал одним из способов теплового воздействия, конкурируя с грелками, микроволновым и радиочастотным излучением. Основной областью использования ультразвуковой терапии было лечение повреждений мягких тканей, хотя ультразвук применялся и для лечения суставов и костей.
Выяснение механизмов воздействия ультразвука стимулировало попытки физиотерапевтов изменить режимы воздействия так, чтобы лучше использовать предполагаемые достоинства нетепловых механизмов. При этом использовались малые интенсивности ультразвука и импульсные режимы работы. Из-за недостатка научно обоснованных, контролируемых клинических экспериментов при подборе режимов ультразвукового воздействия главенствовал эмпирический подход и практически каждая клиника использовала для этого свой «рецепт». Однако по мере того как физиотерапевты овладевали знаниями в области ультразвука, режимы лечения становились более обоснованными. Было бы неправильным слишком критично относиться к тому, как физиотерапевты выбирают параметры ультразвукового воздействия, поскольку необходимая им информация не всегда доступна. До сих пор неизвестно, какие интенсивности ультразвука наиболее эффективны в терапии, например, какая из интенсивностей: SATP или SATA играет более важную роль (см. разд. 3.8). Интуитивно представляется, что тепловые эффекты зависят от общей энергии, т. е. от интенсивности SATA, в то время как для нетепловых эффектов более важна пиковая интенсивность, т. е. SATP.
13.3.1. ОБОРУДОВАНИЕ И МЕТОДИКИ
Серийно выпускается большое разнообразие ультразвуковых медицинских приборов. Как правило, они имеют малый вес и достаточно портативны. Многие из приборов используют ультразвук средней по пространству интенсивности до 3 Вт/см2 и работают в частотном диапазоне 0,75—5 МГц. Используются либо непрерывный, либо импульсный режимы. Импульсные режимы выбираются главным образом в том случае, когда хотят использовать нетепловые эффекты. Более точно режимы подбираются эмпирически. Выбор несущей частоты определяется глубиной расположения объекта воздействия: более высокие частоты используются для воздействия на поверхностные области. Серийные генераторы обычно имеют две или три фиксированные рабочие частоты, часто с взаимозаменяемыми преобразователями, и дают возможность плавно или дискретно менять интенсивность. Большинство приборов обладают возможностью работать в одно- или двухимпульсных режимах. Наиболее часто используемые режимы 2 мс : 2 мс (сигнал : пауза) или 2 мс : 8 мс. Импульсные режимы обычно характеризуются либо отношением длительности сигнала к длительности паузы, либо коэффициентом заполнения — отношением длительности сигнала к периоду следования импульсов, выраженным в процентах. В любом случае для полного описания импульсного режима необходимо приводить длительность импульса. Все приборы обычно снабжены таймером, чтобы задавать длительность процедуры. Опубликованные обследования ультразвуковых терапевтических генераторов, используемых в клиниках, показывают, что их заводская калибровка крайне неточна (см., например, [77, 83]). Репачоли с соавт. [77] привели данные о том, что у 37 проверенных ими приборов, эксплуатируемых в районе Оттавы, уровень выходной мощности в 3—3,5 раза отличался от показаний встроенного индикатора, при этом при работе в непрерывном режиме 72% приборов излучали меньшую акустическую мощность по сравнению с показаниями индикатора.
Проверялись также таймеры, и хотя большинство из них имело точность в пределах 5%, 40% из них имели более высокую погрешность, достигавшую в некоторых случаях 20%. Согласно обзору Стюарта и наблюдениям автора, можно найти приборы, которые совсем не излучают акустической энергии, хотя индикатор дает какие-то показания.
Существует несколько простых способов убедиться, излучает ли прибор или нет. Некоторые физиотерапевты покрывают поверхность преобразователя слоем контактного вещества и поворачивают ручку интенсивности до тех пор, пока на поверхности не появится рябь. Можно опустить преобразователь в воду излучающей поверхностью к поверхности воды. Тогда при увеличении интенсивности на поверхности воды возникает рябь, которая чаще всего выглядит как фонтанчик.
Средняя по пространству интенсивность ультразвука терапевтических уровней может быть измерена с помощью простых балансных радиометров [44, 80], а распределения амплитуды ультразвука в пучке могут быть получены с помощью миниатюрных датчиков давления или температуры [96]. Все эти методы описаны в гл. 3.
Терапевтические излучатели обычно сделаны в виде дисков из высокодобротной пьезокерамики цирконат-титаната свинца, например PZT 4. Они помещаются в водонепроницаемую оболочку из алюминия или нержавеющей стали, прикрепленную к концу легкой ручки. Обратная сторона диска граничит с воздухом. Типичный способ закрепления кристалла показан на рис. 13.1. Пространственная картина поля типичного серийного терапевтического преобразователя показана на рис. 13.2.
Существует несколько способов введения ультразвуковой энергии в обрабатываемую область. Наиболее распространенный способ — контактный, когда преобразователь прикладывается непосредственно к коже. В этом случае передача акустической энергии осуществляется через тонкий слой контактного вещества, акустический импеданс которого близок к импедансу кожи.
При лечении частей тела неудобных конфигураций, например колен или локтей, облучение можно проводить при погружении тела в ванну с водой.
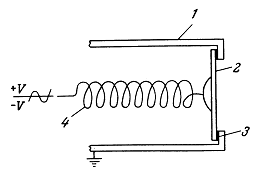
Рис. 13.1 Схема крепления кристалла в терапевтическом излучателе, обеспечивающая воздушную нагрузку тыльной стороны кристалла: 1 — заземленный металлический корпус; 2 — пьезоэлектрический кристалл с серебряными электродами с обеих сторон; 3 — припой; 4 — пружина, прижимающая контакт к обратной стороне.
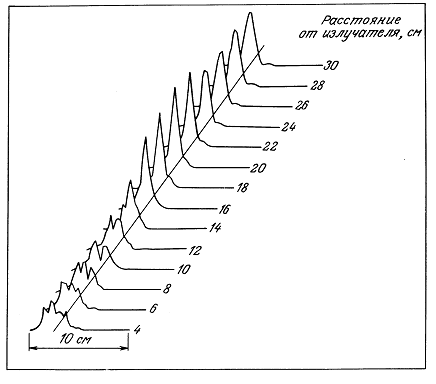
Рис. 13.2. Распределение акустического поля, создаваемого стандартным терапевтическим излучателем на частоте 1,1 МГц.
Также могут использоваться акустически прозрачные мешки с водой. Мешок может принимать форму облучаемой части тела, а акустический контакт с кожей осуществляется через слой контактного вещества.
Обычно в качестве контактных веществ используются легко стерилизуемые жидкости с подходящим акустическим импедансом, такие как минеральное или парафиновое масла. Используются и тик-сотропные вещества (типа гелей). Их удобно использовать, поскольку в обычном состоянии они достаточно вязки, но под действием ультразвука разжижаются. Судя по опубликованным данным сравнительного изучения различных контактных жидкостей, количество энергии, передаваемое через различные жидкости, практически одно и то же, если слой достаточно тонок, и зависит скорее от давления преобразователя на контактное вещество, чем от его состава [87].
Во время процедуры преобразователь может удерживаться в одном положении (режим стационарного излучателя) или непрерывно перемещаться над обрабатываемой областью (режим движущегося излучателя). При любой возможности необходимо избегать режима стационарного излучателя, поскольку возможно образование стоячих волн и «горячих точек», которые могут привести к локальным повреждениям.
13.3.2. ИСПОЛЬЗОВАНИЕ УЛЬТРАЗВУКА В ФИЗИОТЕРАПИИ
Ультразвук в физиотерапии применяется главным образом при лечении повреждений мягких тканей, для ускорения заживления ран, для рассасывания отеков, для размягчения рубцов и во многих других случаях. Он применяется также при костных патологиях и нарушениях кровообращения.
13.3.2.1. Повреждения мягких тканей
Одно из наиболее распространенных применений ультразвука в физиотерапии — это ускорение регенерации тканей и заживления ран. Общие соображения в пользу такого применения недостаточно серьезны, хотя проведенные Дайсон и др. [16—18] экспериментальные исследования весьма интересны. Так, из обеих ушных раковин кролика вырезались кусочки тканей, после чего одно ухо облучалось ультразвукам, а другое оставалось в качестве контрольного. На рис. 13.3 показан ход заживления облученного уха в сравнении с контрольным. На графике видны два подъема в скорости заживления. Наибольшая скорость заживления наблюдалась при облучении импульсным ультразвуком интенсивностью 0,5 Вт/см2 SATP в режиме 2 мс : 8 мс (сигнал : пауза), но и непревывное облучение интенсивностью 0,1 Вт/см2 приводило к близкому результату. Облучение в импульсном режиме 1 мс : 79 мс интенсивностью 8 Вт/см2 приводило к увеличению пораженного участка. Все три испытываемых режима имели одну и ту же среднюю по времени интенсивность. Облучение ультразвуком интенсивностью 0,5 Вт/см2 в импульсном режиме 2 мс : 8 мс приводило к более быстрому заживлению раны, чем при интенсивности 0,25; 1,5; 2 или 4 Вт/см2 в том же режиме.
Восстановление ткани лучше всего описать с помощью трех перекрывающихся фаз. В течение воспалительной фазы фагоцитарная активность макрофагов и полиморфонуклеарных лейкоцитов ведет к удалению клеточных фрагментов и патогенных частиц.
Рис. 13.3. Влияние ультразвука на заживление тканей уха кролика при различных режимах облучения с эквивалентной тепловой дозой. По вертикальной оси отложено К — отношение площади заживления в облученном ухе к площади заживления в контрольном ухе. 1 — Непрерывный звук, 0,1 Вт/см2, ![]() T = 1,3° С; 2 — импульс 2 мс, пауза 8 мс, 0,5 Вт/см2,
T = 1,3° С; 2 — импульс 2 мс, пауза 8 мс, 0,5 Вт/см2, ![]() T = 1,6° С; 3 — импульс 1 мс, пауза 79 мс, 8 Вт/см2,
T = 1,6° С; 3 — импульс 1 мс, пауза 79 мс, 8 Вт/см2, ![]() Т= 1,6° С [18].
Т= 1,6° С [18].
Переработка этого материала происходит главным образом при помощи лизосомальных ферментов макрофагов. Известно, что ультразвук терапевтических интенсивностей может вызывать изменения в лизосомальных мембранах, тем самым ускоряя прохождение этой фазы.
Вторая фаза в залечивании ран — пролиферация или фаза разрастания. Клетки мигрируют в область поражения и начинают делиться. Образуется гранулированная ткань и фибробласты начинают синтезировать коллаген. Интенсивность заживления начинает увеличиваться, и специальные клетки, миофибробласты, заставляют рану стягиваться. Показано, что ультразвук значительно ускоряет синтез коллагена фибробластами как in vitro, так и in vivo.
В работе [42] показано, что если первичные диплоидные фибробласты человека облучить ультразвуком частотой 3 МГц и интенсивностью 0,5 Вт/см2 in vitro, то количество синтезированного белка увеличится. Исследование облученных клеток в электронном микроскопе показало, что по сравнению с контрольными клетками в них содержится больше свободных рибосом, больше растяжение грубого эндоплазматического ретикулума, больше цитоплазменная вакуолизация, больше автофаговых вакуолей и больше повреждений лизосомальных мембран и митохондрий. В последующих работах той же группы [90, 91] показано, что кавитация может стимулировать синтез коллагена. В работе [89] увеличение синтеза коллагена наблюдалось после ультразвукового облучения фибробластов in vivo. В работах [74, 75] приведены экспериментальные свидетельства того, что ультразвук стимулирует грануляцию ткани.
Третья фаза — восстановление. Эластичность нормальной соединительной ткани обусловлена упорядоченной структурой колла-геновой сетки, позволяющей ткани напрягаться и расслабляться без особых деформаций. В рубцовой ткани волокна часто располагаются нерегулярно и запутанно, что не позволяет ей растягиваться без разрывов. Это ведет к уменьшению растяжимости и эластичности рубца по сравнению с нормальной окружающей тканью. Есть доказательства, что рубцовая ткань, формировавшаяся при воздействии ультразвука, прочнее и эластичнее по сравнению с «нормальной» рубцовой тканью. Это показывает, что ультразвук влияет на расположение новообразующего коллагена и помогает процессу восстановления.
Драстичова с соавт. [12] исследовали влияние ультразвука (0,85 Вт/см2) на прочность рубцов у морских свинок. Разрезы на их спинках облучались на третий или четвертый день после операции. Разрывное усилие облученных рубцов составляло 189% от контрольных в одной серии опытов и 271% в другой. Дайсон с соавт. [19] изучали воздействие ультразвука (3 МГц, 0,5 Вт/см2) на заживление криохирургических повреждений у крыс. Поврежденные участки облучались на 0, 1, 3, 5 и 7 дни. Разрывное усилие рубцовой ткани через 1 мес. составляло 109% прочности контрольного рубца, через 2 мес. 126% от его прочности. Спустя 2 мес. прочность облученных рубцов достигала 42% прочности нормальной кожи в том же месте.
К сожалению, несмотря на широкое использование ультразвука в терапии, было проведено всего несколько широкомасштабных клинических наблюдений. Одно из них было посвящено лечению хронических варикозных язв на ногах [15]. Язвы облучались ультразвуком частотой 3 МГц интенсивностью 1 Вт/см2 SATP в импульсном режиме 2 мс : 8 мс. После 12 сеансов лечения (3 раза в неделю на протяжении 4 недель) средняя площадь язв составляла 66,4 ± 8,8% от их первоначальной площади, в то время как площадь контрольных язв уменьшилась всего до 91,6 ± 8,9%. Измеренное увеличение температуры в облучаемых зонах не превышало 1° С. Такое увеличение температуры, вызванное другими способами, совершенно недостаточно для наблюдаемой стимуляции заживления, что доказывает нетепловой характер механизма воздействия. В работе [30] было показано, что ультразвук может способствовать приживлению пересаженных лоскутов кожи на краях трофических язв.
С некоторым успехом ультразвук используется для размягчения и увеличения эластичности рубцов и контрактур [6, 67, 76]. Несмотря на достаточную универсальность этого эффекта, механизм воздействия в этом случае неясен; возможно, он связан с комбинацией умеренного нагрева и явления, описанного ранее в этой главе.
Считается, что ультразвук может быть полезен при рассасывании отеков, вызванных повреждениями мягких тканей. В работе [29] было проверено это широко распространенное утверждение (см., например, [71]). Искусственно созданная опухоль у крыс облучалась ультразвуком интенсивностью 0,5 Вт/см2 на частотах 0,75; 1,5; 3,0 МГц в импульсном режиме. Был установлен частотно-зависимый эффект: единственной эффективной оказалась частота 0,75 МГц. Характеристики импульсного режима (2 мс : 8 мс или 2 мс : 2 мс) на эффект не влияли. Механизм, ответственный за рассасывание опухоли, остался невыясненным. Возможно, он обусловлен увеличением кровотока или местными изменениями в тканях под действием акустических микропотоков.
Без более строгих научных исследований этих и других известных явлений все рассуждения о механизмах, приводящих к положительному терапевтическому эффекту (если таковой существует), будут оставаться чисто умозрительными. Только понимание механизмов взаимодействия ультразвука с биологическими тканями позволит получить максимальный лечебный эффект.
13.3.2.2. Костные повреждения
Восстановление повреждений мягких и костных тканей имеет много общего. Оба процесса включают в себя воспалительную, пролиферационную и восстановительную фазы. Хотя и это подобие, и тот факт, что в процессах участвуют однотипные клетки, подталкивали к тому, чтобы исследовать возможность применения ультразвука для лечения костных повреждений, публикаций на эту тему очень мало.
При экспериментальном исследовании переломов малой берцовой кости у крыс было обнаружено, что ультразвуковое облучение во время воспалительной и ранней пролиферационной фаз ускоряет и улучшает выздоровление. Костная мозоль содержала больше костной ткани и меньше хрящей. Однако облучение в поздней пролиферационной фазе приводило к негативным явлениям — усиливался рост хрящей и задерживалось образование костной массы [14]. Обнаружено также, что облучение ультразвуком интенсивностью 0,5 Вт/см2 SATP длительностью 5 мин в импульсном режиме 2 мс : 8 мс более эффективно на частоте 1,5 МГц, чем на частоте 3 МГц. Это позволяет предположить нетепловой механизм воздействия, хотя природа его точно не установлена.
Существуют две основные области применения ультразвука в хирургии. В первой из них используется способность сильно фокусированного пучка ультразвука вызывать локальные разрушения в тканях, а во второй — механические колебания ультразвуковой частоты накладываются на хирургические инструменты типа лезвий, пил, металлических наконечников и др.
13.4.1. ХИРУРГИЯ С ПОМОЩЬЮ ФОКУСИРОВАННОГО УЛЬТРАЗВУКА
Хирургическая техника, которая в перспективе могла бы заменить традиционный скальпель, должна обеспечивать воспроизводимость и управляемость разрушения тканей, воздействовать только на четко ограниченную область, быть быстродействующей и вызывать минимальные потери крови. Мощный фокусированный ультразвук обладает большинством из этих качеств. Фокальная область может иметь типичные размеры 1 -г- 2 мм в ширину и 3^4 мм в длину.
Возможность использования фокусированного ультразвука для создания зон поражения в глубине органа без разрушения вышележащих тканей изучено в основном в операциях на мозге. Именно здесь первоначально возникла необходимость в создании таких разрушений для нужд экспериментальной нейроанатомии. Воздействие осуществлялось и на другие органы: печень, спинной мозг, почки и глаз.
Как показано в гл. 2, фокусирование ультразвука может быть достигнуто многими способами (см. также [35]). Самый простой из них — это использование преобразователя, излучающая поверхность которого по форме представляет собой сферическую вогнутую оболочку, изготовленную из пьезоэлектрического материала. Фокус такого излучателя лежит на его главной оси и располагается вблизи центра кривизны оболочки. Как следует из работ Коссоффа [54] и О'Нейла [70], распределение акустического поля такого излучателя может быть рассчитано. Используя подобные сферические излучатели, Робинсон и Лили [78], а также Уорвик и Понд [88] произвели в мозговой ткани у крыс и кошек разрушения в фокальной области.
Хотя таким способом можно получить нагреваемую область с четко очерченными границами, регулировать глубину зоны поражения в этом случае оказывается не просто. Используя плоский излучатель совместно с различными акустическими линзами, можно добиться изменения глубины области поражения. Так как акустические линзы обычно делаются из материала, имеющего скорость звука больше, чем в воде, то для создания сходящегося пучка необходимо изготовлять линзы вогнутыми (см. гл. 2).
Главное ограничение при использовании набора из таких линз накладывает поглощение ультразвука в материале самих линз. Оптимальная передача энергии осуществляется при условии, когда линзы и излучатель разделены четвертьволновым согласующим слоем. Такие комбинации излучателя с линзами применяли Л инке с соавт. [65] при создании зон поражений в печени у крыс и кроликов и в почках у кроликов.
Фокальная область, используемая в ультразвуковой хирургии, по форме представляет собой эллипсоид вращения, вытянутый в направлении центральной оси звукового поля. Распределение давления вблизи фокуса имеет вид ![]() , а ширина фокального пятна равна (ср. уравнение (2.5))
, а ширина фокального пятна равна (ср. уравнение (2.5))
![]()
где t0 — фокусное расстояние, а — радиус излучателя, а ![]() — длина волны в ткани.
— длина волны в ткани.
Для непоглощающей среды теория дифракции предсказывает, что только 84% энергии излучателя проходит через фокальную область [48]. Однако в ткани всегда имеется реальное поглощение, и эта доля становится еще меньше.
Точная форма любого разрушения зависит от облучаемой ткани. В однородной ткани очаг разрушения будет иметь приблизительно форму эллипсоида. Однако в том случае, когда облучаемый участок состоит из тканей двух типов, один из которых менее чувствителен к ультразвуковому разрушению, то предсказать форму пораженной зоны непросто. Такое случается, например, при облучении мозга, где селективно может быть разрушено белое вещество, так как серое вещество и сосудистая система менее чувствительны к действию ультразвука [28]. Обилие сосудов в ткани также влияет на размеры очага разрушения.
Отношение длины эллипсоида к его ширине зависит от угла, под которым происходит облучение. Из уравнения (13.1) видно, что при увеличении частоты ультразвука ширина фокального пятна уменьшается при заданной величине поглощенной энергии. Коротко говоря, величина экспозиции разрушаемого объема ткани оказывается приблизительно пропорциональной количеству энергии, поглощенному в ткани [51].
Предпринималось несколько попыток, чтобы сравнить все имеющиеся данные по пороговым интенсивностям, при которых происходит разрушение тканей (см. например, [25, 27, 52, 63]). Было сделано эмпирическое предположение (по-видимому, без точной оценки степени его достоверности), что на графике зависимости интенсивности ультразвука от времени экспозиции, построенном в дважды логарифмическом масштабе, можно выделить три линейных участка. При интенсивностях звука меньше 2-103Вт/см2 и времени экспозиции меньше 4-10"2 с, по-видимому, работает кавитационный механизм [27], а в случае, когда время экспозиции превышает 1 с [63], а интенсивность звука меньше чем 200 Вт/см2 [25], вероятно, работает механизм теплового разрушения. В промежуточной области, показанной на рис. 13.4, механизм разрушения неясен. Порог кавитации, измеренный Гавриловым [31] по появлению субгармоники, согласуется с этой классификацией. По мнению Джонстона и Данна [52], по-видимому, существует порог интенсивности в области 30![]() 40 Вт/см2 для времени экспозиции 102
40 Вт/см2 для времени экспозиции 102![]() 103 с. Для интенсивности и времени экспозиции, при которых в ткани наступают разрушения, было предложено следующее соотношение:
103 с. Для интенсивности и времени экспозиции, при которых в ткани наступают разрушения, было предложено следующее соотношение:
![]()
где с — слабая функция частоты и, возможно, исходной температуры ткани [13]. При попытке найти механизм развития разрушений было обнаружено, что пороговые кривые можно предсказать заранее, если считать, что связь между напряжением и деформацией в ткани нелинейна и существует гистерезис [52], и что ультразвук распространяется в ткани в виде плоской волны.
Рис. 13.4. Диаграмма интенсивность — время воздействия, показывающая пороги разрушения тканей фокусированным ультразвуком (двойной логарифмический масштаб). Линия соответствует соотношению ![]() (см. текст). Выделены области с преобладающим влиянием кавитационного и теплового механизмов разрушений.
(см. текст). Выделены области с преобладающим влиянием кавитационного и теплового механизмов разрушений.
Изучение зоны поражений под микроскопом, выполненное Уорвиком и Пондом [88], показывает, что разрушения имеют структуру «остров» и «ров», причем существует резкая граница между нормальной и пораженной тканью. Подобные разрушения наблюдались Пондом [73] в результате нагрева тонкой проволочки, вживленной в ткань. В мозговой ткани «остров» представляет собой коагулированную центральную часть, а «ров» характеризует разрыхление цитоплазмы нервных клеток, хотя при этом кровеносные сосуды могут остаться нетронутыми. Изучение ткани с помощью электронного микроскопа показывает, что вначале разрушаются митохондрии; они набухают и приобретают низкую электронную плотность. Однако в мозге наиболее чувствительными оказываются синапсы и они разрушаются еще раньше [7, 22].
Воздействие фокусированным ультразвуком применялось в экспериментальной нейрохирургии для изучения функций мозга [26] и для перерезки мозолистого тела мозга при изучении поведенческих реакций [59]. Использование этой методики при лечении людей до сих пор было лимитировано необходимостью удалять часть черепа для создания акустически прозрачного «окна», через которое можно было бы пропускать ультразвуковой пучок. Фокусированный ультразвук был использован также для воздействия на глаз [10, 66] и почку [65].
Взамен традиционной хирургии ультразвук может применяться и при лечении болезни Меньера. Сущность болезни состоит в нарушениях во внутреннем ухе, что приводит к приступам головокружения. Цель лечения направлена на уменьшение головокружений при сохранении достаточного уровня слуха. Тонкий ультразвуковой пучок большой интенсивности направляется на латеральный полукружный канал уха для разрушения нейроэпителия кристы и макулы в лабиринте. Для этого метода лечения очень важна точная дозиметрия [2, 92], поскольку вблизи полукружного канала проходит лицевой нерв и разрушение этого нерва ведет к лицевому параличу.
Хотя применение ультразвука для этой цели было впервые предложено в 1948 г. [81], первый полный отчет о его использовании для выключения вестибулярной функции появился только в 1952 г. Именно тогда Крейси применил ультразвук интенсивностью 4 Вт/см2 в течение 15 мин для лечения болезни. Спустя 11 мес. больной освободился от шума в ушах и головокружений, но при этом ухудшился слух.
Часто используемая методика описана Арсланом [4]. В сосцевидном отростке височной кости проделывается желобок, в который вводится ультразвуковой излучатель. Это позволяет облучить лабиринт. Вызывается нистагм, больной испытывает головокружение и его глаза поворачиваются в направлении, в котором он чувствует, что падает. После разрушения нервных окончаний в лабиринте, нистагм изменяет направление. Это указывает на успех операции. Во время процедуры пациент находится под местной анестезией.
Применяя модифицированный метод лечения Арслана, Соренсен и Андерсен [82] обнаружили, что 72% больных на продолжительное время избавляются от приступов головокружения, при этом слух большинства пациентов остается без изменений. При анализе результатов лечения болезни Меньера ультразвуком Сёберг [81] показал, что процент освобождения от приступов головокружения высок и составляет от 67 до 95%. При этом слух в основном либо не изменяется, либо слегка улучшается. В большинстве случаев шум в ушах не пропадал.
Единственный риск в методике лечения болезни, развитой Арс-ланом, состоит в возможном поражении лицевого нерва, что ведет к лицевому параличу. Чтобы уменьшить этот риск, Коссоффом с соавт. [55, 56] был развит метод круглого окна. В группе из 59 пациентов никто не пострадал от лицевого паралича и 80% больных избавились от головокружения после одного или двух сеансов облучения.
13.4.3. ИНСТРУМЕНТАЛЬНАЯ УЛЬТРАЗВУКОВАЯ ХИРУРГИЯ
Ультразвуковые хирургические инструменты состоят обычно из полуволнового магнитострикционного или пьезокерамического преобразователя, связанного с волноводом, имеющим рабочий наконечник, форма которого соответствует выполняемым операциям. Амплитуда колебаний наконечника может составлять от 15 до 350 мкм, а рабочая частота выбирается из диапазона до 30 кГц.
Поскольку трение между двумя поверхностями уменьшается, если одна из поверхностей колеблется, то применение ультразвуковых инструментов для разреза требует меньших усилий по сравнению с традиционными скальпелями [33]. Высокая температура, достигаемая на конце ультразвукового скальпеля, может прижигать сосуд до 2 мм в диаметре [11]. Это уменьшает кровотечение в операционной зоне и, таким образом, облегчает проведение операции.
Преимущество ультразвуковой техники по сравнению с криохирургической состоит в том, что кончик скальпеля не прилипает к ткани, и поверхности разреза не испытывают дополнительных травм. Преимущество ультразвукового скальпеля по сравнению с лазерной хирургией заключается в том, что хирург чувствует сопротивление ткани при ее разрезе и поэтому разрушение ткани лучше контролируется [45].
Ультразвуковые инструменты нашли множество применений в клинике, среди которых можно выделить две большие области. К первой относится аспирация (удаление) ткани. Возможно, здесь наиболее распространенным случаем использования ультразвука является удаление катаракты из хрусталика глаза (факоэмульсифика-ция). Кончик инструмента делается в форме полой трубочки, которая вставляется в небольшое отверстие в глазу. Кончик вибрирует, разрушая хрусталик, и небольшие его фрагменты высасываются через трубочку [53]. Аналогичная методика может быть использована и для уменьшения объема твердой опухоли, например, ректальной [45].
К второй области применения ультразвуковых инструментов относится разрезание тканей. Как уже упоминалось выше, достоинством здесь являются малые потери крови. Метод успешно применяется при операциях на таких богатых сосудами органах, как печень и селезенка. Он используется также при трахеотомии, тонзиллэктомии, при операциях на легких, бронхах, грудной клетке и глазе [11, 33, 45]. Для резания кости может применяться ультразвуковая пила. При сравнительном исследовании было найдено, что поверхность разреза, произведенного ультразвуковой пилой, была шероховатее, чем сделанная обычной пилой, однако она не содержала видимых микротрещин [3]. Считается, что ультразвуковая пила работает легче и плавнее, и с ее помощью легче осуществлять точную остеотомию. Сначала заживление кости после ультразвуковых разрезов происходит медленнее, чем при обычном разрезе, однако спустя шесть недель заживление происходит одинаково в обоих случаях.
Область медицинской акустики, основанная на применении ультразвуковых хирургических инструментов является одной из наименее изученных. Из существующих сообщений, содержащих мало количественной информации, следует, что такие инструменты действительно могут получить широкое практическое использование. Необходимы тщательные научные и инженерные разработки, чтобы выявить весь потенциал, заложенный в этой области.
Впервые в 1955 г. Циннер [97] предложил использовать ультразвук для лечения периодонтита; он же предложил использовать ультразвук для удаления камней.
Инструмент, используемый для лечения зубов, состоит из стержневого ультразвукового преобразователя и имеет на конце наконечник, удобный для работы [21]. В наконечнике возбуждаются продольные колебания на частоте в диапазоне 25—42 кГц и с амплитудой в области 6—100 мкм [85].
Ультразвуковая очистка позволяет счистить и удалить налипшие скопления с поверхностей зубов и их корней. Наконечником можно чистить, соскабливать, стирать и шлифовать зубы, избавляя их от камней, бляшек,- остатков пищи, пятен и размягченного цемента. Ультразвук необходим при лечении язвенного воспаления десен (гингивита), краевого гингивита и перикоронита. Ультразвуковые инструменты могут использоваться для кюретажа (выскабливания патологического зубодесневого кармана). В этом случае наконечник может прикладываться к мягкой ткани для того, чтобы произвести слабый ожог.
Анализ ряда сообщений об эффективности применения ультразвука при очистке зубов показывает, что в этом случае от врача требуется меньше усилий, уменьшается дискомфорт самого пациента, а время очистки сокращается по сравнению с ручной процедурой; конечный результат один и тот же. Считается, что ультразвук более эффективен для удаления пятен [85]. Фотомикрографические исследования показали, что после ультразвуковой очистки поверхность зуба становится более гладкой, чем после ручной обработки [20].
13.5. УЛЬТРАЗВУК ПРИ ЛЕЧЕНИИ РАКА
Первое упоминание о возможности применения ультразвука для воздействия на раковую опухоль содержалось в заметке, опубликованной в журнале «Nature» в 1933 г., в которой утверждалось, что специфическое воздействие на карциному Эрлиха отсутствовало [86]. С этого момента энтузиазм, связанный с возможностью применения ультразвука как противоопухолевого агента, начал колебаться, отражая в основном популярность гипертермии.
На протяжении ряда лет вплоть до 1949 г. несколько групп исследователей изучали возможность применения ультразвука в онкологии как самого по себе, так и в сочетании с рентгеновским облучением. В 1944 г. появилась первая работа об успешном применении ультразвука при лечении опухолей (кожных метастазов) у человека [47]. В 1949 г. на конференции в Ерлангене (Германия) ученые пришли к заключению, что чрезмерный энтузиазм по поводу перспектив использования ультразвука в онкологии не подтвержден клиническими данными и что «применение ультразвука необходимо прекратить» [58]. После этого исследовательский пыл в этом направлении несколько угас.
Оживление интереса к использованию при терапии рака тепла как самого по себе, так и в сочетании с рентгеновским облучением или химиотерапией [23], снова возбудили интерес к лечению опухолей ультразвуком.
Исследования начались в трех направлениях, а именно в применении ультразвука самого по себе, а также возможности его использования совместно с ионизирующим облучением или с противоопухолевыми лекарственными веществами.
Нет сомнений, что ультразвук достаточной интенсивности может нагреть любую локализованную область ткани до используемых в гипертермии температур (больше 42° С, см. разд. 12.1.2). С технической точки зрения преимущество ультразвука перед электромагнитным нагревом состоит в том, что выделение энергии в среде может быть лучше локализовано, при необходимости используя фокусировку. Способы достижения требуемых распределений температур рассматривались в гл. 2 и в нескольких обзорных статьях (см., например, [35, 49]). Они основаны на использовании системы линз, вогнутых преобразователей, системы зеркал, скрещивающихся звуковых пучков и сфазированных антенных решеток. Нужное распределение температур зависит от размера и формы опухоли, подвергаемой лечению, и ее местоположения в теле. В целом задача состоит в том, чтобы равномерно нагреть весь объем опухоли до некоторой постоянной температуры при условии, чтобы температура нормальной ткани поддерживалась на физиологически приемлемом уровне. На практике опухоль нагревают до некоторой приемлемой минимальной температуры; при этом часть окружающей нормальной ткани тоже нагревается, поскольку очень важно, чтобы температура на периферии опухоли также достигала гипертермического уровня. Широкий набор необходимых распределений температур означает, что методика нагрева должна быть чрезвычайно гибкой. Температуры должны измеряться точно, что делают инвазивно с помощью термойдрных датчиков.
Есть указания на то, что кроме чисто температурного действия ультразвук может обладать и некоторым цитотоксическим эффектом. Ли с соавт. [64] и тер Хаар с соавт. [37] показали это, облучая in vitro клетки, которые поддерживались при гипертермической температуре. Обнаружено, что потеря репродуктивной способности, как показано экспериментами с клонированием, в облученных образцах была больше, чем в образцах, нагретых обычным способом (рис. 13.5,(2). Механизм гибели клеток неизвестен, хотя Мортон с соавт. [69] показали, что с теплом или кавитацией его природа не связана.
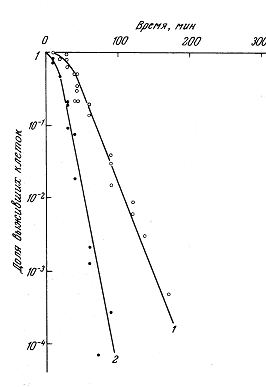
Рис. 13.5а. Влияние ультразвука частотой 3 МГц и интенсивностью 3 Вт/см2 и нагрева до 43° С на выживаемость клеток in vitro: 1 — нагрев; 2 — нагрев плюс ультразвук.
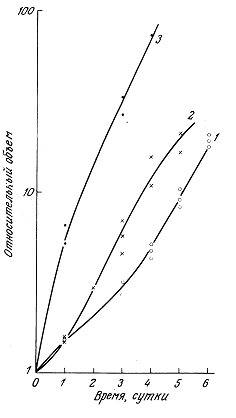
Рис. 13.56. Рост многоклеточных сфероидов после выдержки их в течение 60 мин при 43° С: 1 — с одновременным облучением ультразвуком; 2 — без ультразвука; 3 — контроль, выдержка 60 мин при 37° С.
Подобное явление наблюдалось и у многоклеточных сфероидов (рис. 13.56). Это характеризует влияние ультразвука на клетки, находящиеся при гипертермических температурах. Воздействие ультразвука при температуре в 37° С и тех же прочих условиях не влияет на степень выживаемости клеток.
Данные о синергизме, т. е. о совместном действии ультразвука и рентгеновского облучения несколько противоречивы. Первые сообщения Вебера [94, 95] указывали на то, что если ультразвук применяется в комбинации с рентгеновскими лучами как в карциноме Уокера у крыс, так и для некоторых опухолей у человека (в основном облучались базально-клеточный рак и плоскоклеточная карцинома), то доза радиотерапии может быть уменьшена на 30—40% по сравнению с применением одной только радиотерапии. Использование одного только ультразвука никакого эффекта на опухоли не оказывает.
Другие исследователи обнаружили, что эффективность применения ультразвука в комбинации с рентгеновским облучением может зависеть от вида опухоли [93], и в некоторых случаях может отсутствовать [9]. Возможно, что эффект зависит как от радиочувствительности опухоли, так и от распределения температуры, достигаемого внутри опухоли. Если опухоль не прогрета однородно, то возможно, что минимальная достигнутая температура и определяет успех лечения [39].
Изучение совместного использования ультразвука и химиотера-певтических агентов также породило множество противоречивых результатов. Первое предложение использовать ультразвук совместно с азотистым ипритом (мехлорэтамином) было высказано Хиллом [43] в 1967 г. Однако этого совместного эффекта не было найдено. Тем не менее девять лет спустя Кремкау с сотр. [57] обра-ружил, что если мышам ввести опухолевые клетки (лейкемии L 1210), которые были обработаны in vitro до инъекции ультразвуком и азотистым ипритом, то эти мыши жили дольше, чем при введении клеток, обработанных только одним из агентов. В подобных же экспериментах с другими лекарственными веществами 5 из 10 вызывали подобное же увеличение, но никакого объяснения этого явления так и не было обнаружено. Было предположено, что присутствие этих цитотоксических агентов препятствует пораженным клетках восстанавливать повреждения, вызванные ультразвуком, и наоборот [58]. По своей природе механизм этого явления может быть частично тепловым.
Если ультразвук используется как средство гипертермии в комбинации с химиотерапевтическими веществами, то при выборе подходящих лекарственных препаратов должно быть принято во внимание несколько факторов. Препараты должны быть более цито-токсичными при гипертермических температурах, чем при 37° С, и должны активироваться в пределах опухоли. Только в этом случае избирательный нагрев опухоли может дать терапевтический эффект. В результате исключается использование в этих целях, например, циклофосфамидов, которые активируются в печени [62].
Очень трудно вынести общее заключение об эффективности применения ультразвука в терапии рака. Результаты Вебера, приведенные на рис. 13.6, показывают значительное увеличение эффективности рентгеновского облучения в комбинации с использованием ультразвука.
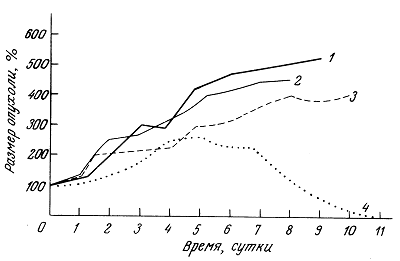
Рис. 13.6. Данные Вебера [95], показывающие, что совместное действие ультразвука и рентгеновских лучей на опухоли крыс более эффективно, чем их действие по отдельности; 7 — контроль; 2 — ультразвук; 3 — рентгеновские лучи; 4 — рентгеновские лучи плюс ультразвук.
При лечении поверхностных новообразований у людей [38] у 12% обнаружена полная регрессия, у 42% — частичная регрессия, а у 46°/о не наблюдалось никакой реакции. Наилучшие результаты лечения отмечались в случае плоскоклеточной карциномы головы и шеи. На рис. 13.7 представлены обобщенные результаты по воздействию на рост опухолей, взятые из литературных источников до 1979 г. Кажется логичным предположить, что если клетки опухолей чувствительны к теплу, то эти опухоли можно успешно лечить с помощью ультразвука. Не исключено, что и другие виды опухолей можно лечить, если нетепловые эффекты ультразвука приводят к их регрессии.
Очевидно, что ультразвук может играть важную роль в гипертермическом лечении опухолей. Методика нагрева поверхностных опухолей, расположенных на глубинах меньше 3—4 см, уже существует и используется в повседневной клинической практике в некоторых медицинских центрах. Тем не менее необходимы дальнейшие исследования механизма воздействия и развитие приборного обеспечения для создания надежных воспроизводимых методик нагрева глубоко расположенных опухолей. В общем, следует надеяться, что если возможно осуществить ультразвуковое сканирование опухоли, то можно будет и ее нагреть.
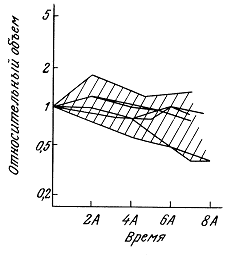
Рис. 13.7. Диаграмма, показывающая реакцию опухолей различного типа на ультразвуковую терапию [58]. А составляет либо 1 либо 3 суток в зависимости от типа опухоли. Диаграмма демонстрирует разброс реакций, о котором сообщалось в литературе.
Биофизика гибели клеток под воздействием ультразвука при повышенных температурах слабо изучена. По-видимому, всякий раз, когда проявляется нетепловой механизм взаимодействия, он оказывается вторичным по отношению к тепловому эффекту. Если это так, то наружные клеточные мембраны, по-видимому, являются наиболее вероятной мишенью разрушающего действия ультразвука. Это может быть особенно важным при совместном использовании нагрева и других противоопухолевых агентов. Механизмы такого комбинированного действия требуют дополнительных исследований, и, как только они станут известны, появится возможность заранее определять условия ультразвукового воздействия, которые позволят достичь максимальной противоопухолевой эффективности ультразвука.
1. Abramson, D. I., Burnett, С, Bell, Y., Tuck, S., Rejal, H., & Fleischer, C.J. (1960) Changes in blood flow, oxygen uptake and tissue temperatures produced by therapeutic physical agents. I. Effect of ultrasound. Am. J. Phys. Med. 39 51—62.
2. Angell James, J. (1967) Clinical aspects of the surgical treatment of Meniere's disease with ultrasound. Ultrasonics 5 102—104.
3. Aro, H., Kallioniemi, H., Aho, A. J., & Kellokumpu-Lehtinen, P. (1981) Ultrasonic device for bone cutting. Acta Orthop. Scand. 52 5—10.
4. Arslan, M. (1953) Treatment of Meniere's syndrome by direct application of ultrasound waves to the vestibular system. Proc. 5th Int. Cong. Otorhinolaryngol. Amsterdam. 429—436.
5. Backlund, L., & Tisellus. P. (1967) Objective measurement of joint stiffness in rheumatoid arthritis. Acta Rheum. Scand. 13 275.
6. Bierman, W. (1954) Ultrasound in the treatment of scars. Arch. Phys. Med. Rehab. 35 209—214.
7. Borrelli, M. J., Bailey, К. I., & Dunn, F. (1981) Early ultrasonic effects upon mammalian CNS structures (chemical synopses). J. acoust. Soc. Am. 69 1514—1516.
8. Chapman, I. V., Macnally, N. A., & Tucker, S. (1979) Ultrasound induced changes in rates of influx and efflux of potassium ions in rat thymocytes in vitro. Ultrasound in Med. & Biol. 6 47—58.
9. Clarke, P. R., Hill, C. R., & Adams, K. (1970) Synergism between ultrasound and X-rays in tumour therapy. Brit. J. Radiol. 43 97—99.
10. Coleman, D. J., Lizzi, F. L., El-Mofty, A. A. M., Driller, J., & Franzen, L. A. (1980) Ultrasonically accelerated resorption of vitreous membranes. Am. J. Oph-thalm. 89 490—499.
11. Derderian, G. P., Walshaw, R., & McGehee, J. (1982) Ultrasonic surgical dissection in the dog spleen. Am. J. Surgery 143 269—273.
12. Drastichova, V., Samohyl, J., & Slavetinska, A. (1973) Strengthening of sutured skin wound with ultrasound in experiments on animals. Acta Chir. Plast. (Pra-ha) 15 114—119.
13. Dunn, E, Lohnes, J. E., & Fry, F. J. (1975) Frequency dependence of threshold ultrasonic dosages for irreversible structural changes in mammalian brain. J. acoust. Soc. Am. 58 512—514.
14. Dyson, M., & Brookes, M. (1983) Stimulation of bone repair by ultrasound in Ultrasound '82 ed. Lerski, R. A., Morley, P. Pergamon Press, pp. 61—66.
15. Dyson, M., Franks, C, & Suckling, J. (1976) Stimulation of healing of varicose ulcers by ultrasound. Ultrasonics 14 232—236.
16. Dyson, M., Pond, J. В., Joseph, J., & Warwick, R. (1968) The stimulation of tissue regeneration by means of ultrasound. Clin. Sci. 35 273—285.
17. Dyson, M., & Pond, J. B. (1970a) The effect of pulsed ultrasound on tissue regeneration. Physiotherapy 56 136—142.
18. Dyson, M., Pond, J. В., Joseph, J., & Warwick, R. (1970b) Stimulation of tissue regeneration by pulsed plane wave ultrasound. IEEE Trans. Sonics and Ultrasonics SU-17 133—144.
19. Dyson, M., Webster, D. E, Pell, R., & Crowder, M. (1979) Improvement in the mechanical properties of scar tissue following treatment with therapeutic levels of ultrasound in vivo Pro. 4th Eur. Symp. Ultrasound in Biology & Medicine, ed. P. Greguss. 1, 129—134.
20. Ewen, S. J. (1966) A photomicrographic study of root scaling Periodontics 4 273—277.
21. Ewen, S. J., & Glickstein, C. (1968) Ultrasonic instrumentation for dentistry. Chapter 2 in Ultrasonic therapy in periodontics. Pub. С. C. Thomas, Springfield, Illinois, U. S. A.
22. Fallon, J. Т., Stehbens, W. E., & Eggleton, R. C. (1973) An ultrastructural study of the effect of ultrasound on arterial tissue. J. Path. Ill 275—284.
23. Field, S. В., & Bleehen, N. M. (1979) Hyperthermia in the treatment of cancer. Cancer Treatment Reviews 6 63—94.
24. Fountain, F. P., Gersten, J. W., & Sengir, O. (1960) Decrease in muscle spasm produced by ultrasound, hot packs and infrared radiation. Arch. Phys. Med. 41 293—298.
25. Frizzell, L. A., Linke, C. A., Carstensen, E. L., & Fridd, C. W. (1977) Thresholds for focal ultrasonic lesions in rabbit kidney, liver and testicle. IEEE Trans. Biomed. Engng. BME-24.
26. Fry, F. J. (1978) Intense focused ultrasound: its production, effects and utilization. In: Ultrasound: its applications in medicine and biology, ed. F. J. Fry Part II, Vol. Ill of Methods and phenomena: their applications in science and technology. Elsevier Scientific Pub. Col. Chapter XIV pp. 689—736.
27. Fry, F. J. Kossoff, G., Eggleton, R. C, & Dunn, F. (1970) Threshold ultrasonic dosages for structural changes in the mammalian brain. /. acoust. Soc. Am. 48 1413—1417.
28. Fry, W. J., Barnard, J. W., Fry, F. J., Krumins, R. F., & Brennan, J. F. (1955) Ultrasonic lesions in the mammalian central nervous system. Science 122 517—518.
29. Fyfe, M., & Chahl, L. A. (1980) The effect of ultrasound on experimental oedema in rats. Ultrasound in Med. & Biol, 6 107—111.
30. Galitsky, А. В., & Levina, S. I. (1964) Vascular origin of trophic ulcers and application of ultrasound as pre-operative treatment to plastic surgery. Acta Chir. Plast. (Praha) 6 271—278.
31. Гаврилов, Л.P. (1974) О физическом механизме разрушения биологических тканей с помощью фокусированного ультразвука. Акуст. ж. 20 № 1 27—32.
32. Gersten, J. W. (1955) Effect of ultrasound on tendon extensibility. Am. J. Phys. Med. 34 362—369.
33. Goliamina, I. P. (1974) Ultrasonic Surgery in: Acoustics. Proc. 8th Int. Congress on Acoustics, London 1974. ed. R. W. B. Stephens, pp. 63—69.
34. ter Haar, G. R., Dyson, M., & Talbert, D. (1978) Ultrasonically induced contractions in mouse uterine smooth muscle in vivo. Ultrasonics 16 275—276.
35. ter Haar, G. R., & Hand, J. W. (1981) Heating techniques in hyperthermia. III. Ultrasound. Brit. J. Radiol. 54 459—466.
36. ter Haar, G. R., & Hopewell, J. W. (1983) The induction of hyperthermia by ultrasound: its value and associated problems. I. Single, static, plane transducer. Phys. Med. Biol. 28 889—896.
37. ter Haar, G. R., Stratford, I. J., & Hill, C. R. (1980) Ultrasonic irradiation of mammalian cells in vitro at hyperthermic temperatures. Brit. J. Radiol. 53 784—789.
38. Hahn, G. M., Li, G. C, Marmor, J. В., & Pounds, D. W. (1980) Thermal and nonthermal effects of ultrasound. In: Radiation biology in cancer research ed. R. E. Meyn., & H. R. Wither. Reven Press, New York, pp. 623—636.
39. Hahn, G. M., & Pounds, D. (1976) Heat treatment of solid tumours: why and how. Appl. Radiol. 5 131—144.
40. Hand, J. W. & ter Haar, G. R. (1981) Heating techniques in hyperthermia. Brit. J. Radiol. 54 443—466.
41. Harvey, E. N., & Loomis, A. L. (1928) High frequency sound waves of small intensity and their biological effects. Nature 121 622.
42. Harvey, W., Dyson, M., Pond, J. В., & Grahame, R. (1975) The in vitro stimulation of protein synthesis in human fibroblasts by therapeutic levels of ultrasound. In: Ultrasonics in medicine, (ed: E. Kazner et al.) pp. 10—21 Excerpta Medica, Amsterdam. International Congress Series No. 363.
43. Hill, С. R. (1967) Changes in tissue permeability produced by ultrasound. Brit. J. Radiol. 40 317.
44. Hill, C. R. (1970) Calibration of ultrasonic beams for bio-medical applications. Phys. Med. Biol. 15 241—248.
45. Hodgson, W. J. B. (1979) The Ultrasonic Scalpel. Bull. N. Y. Acad Med. 55 908—915.
46. Hogan, R. D., Franklin, T. D., Fry, F. J., Avery, K. A., & Burke, К. M. (1982) The effect of ultrasound on microvascular hemodynamics in skeletal muscle: effect on arterioles. Ultrasound in Med & Biol. 8 45—55.
47. Horvath, J. (1944) Ultraschallwirkung beim menschilchen Sarkom. Strahlentherapie 75 119—125.
48. Hueter, T. F., Ballantine, H. Т., & Cotter, W. C. (1956) Production of lesions in the central nervous system with focused ultrasound: a study of dosage factors. J. acoust. Soc. Am. 28 192—201.
49. Hunt, J. W. (1982) Applications of microwave, ultrasound and radiofrequency heating. In: Third International Symposium: Cancer Therapy by Hyperthermia, Drugs and Radiation. National Cancer Institute Monograph # 61 NIH Publication # 82—2437 pp. 447—456.
50. Imig, C. J., Randall, B. F., & Hines, H. M. (1954) Effect of ultrasonic energy on blood flow. Am. J. Phys. Med. 33 100—102.
51. Johnston, R. L., & Dunn, F. (1976) Ultrasonic absorbed dose, dose rate, and produced lesion volume. Ultrasonics 14 153—155.
52. Johnston, R. L., & Dunn, F. (1981) Ultrasonic hysteresis in biological media. Environ./Biophys. 19 137—148.
53. Kelman, C. D. (1967) Phacoemulsification and aspiration: a new technique of cataract removal. Am. J. Ophthalm. 64 23—35.
54. Kossoff, G. (1979) Analysis of focusing action of spherically curved transducers. Ultrasound in Med. Biol. 5 359—365.
55. Kossoff, G., & Khan, A. E. (1966) Theatment of vertigo using the ultrasonic generator. Arch. Otol. 84 181—188.
56. Kossoff, G. Wadsworth, J. R., & Dudley, P. F. (1967) The round window ultrasonic technique for the treatment of Meniere's disease. Arch. Otolaryngol. 86 534.
57. Kremkau, F. W., Kaufmann, J. S., Walker, M. M., Burch, P. G., & Spurr, C. L. (1976) Ultrasonic enhancement of nitrogen mustard cytotoxicity in mouse leukaemia. Cancer 37 1643—1647.
58. Kremkau, F. W. (1979) Cancer therapy with ultrasound: an historical review. J. Clin. Ultrasound 7 287—300.
59. Lee, A. J., Taberner, P. V., & Halliwell, M. (1979) Severing the corpus callosum in rats using ultrasound: theoretical and experimental correlations. J. acoust. Soc. Am. 66 1292—1298.
60. Lehmann, J. R, Masock, A. J. Warren, C. G., & Koblanski, J. N. (1970) Effect of therapeutic temperatures on tendon extensibility. Arch Phys. Med. Rehab. 51 481—487.
61. Lehmann, J. E, McMillan, J. A., Brunner, G. D., & Blumberg, J. B. (1959) Comparative study of the efficiency of short wave, microwave and ultrasonic diathermy in heating the hip joint. Arch Phys. Med. Rehab. 40 510—512.
62. Lele, P. P. (1979) A strategy for localized chemotherapy of tumours using ultrasonic hyperthermia. Ultrasound in Med. & Biol. 5 95—97.
63. Lerner, R. M., Carstensen, E. L., & Dunn, F. (1973) Frequency dependence of thresholds for ultrasonic production of thermal lesions in tissue. J. acoust. Soc. Am. 54 504—506.
64. Li, G. C, Hahn, G. M., & Tolmach, L. J. (1977) Cellular inactivation by ultrasound. Nature 267 163—165.
65. Linke, C. A., Carstensen, E. L., Frizzell, L. A., Elbadawi, A., & Fridd, C. W. (1973) Localised tissue destruction by high intensity focused ultrasound. Archives of Surgery 107 887—891.
66. Lizzi, F. L., Coleman, D. J., Driller, J., & Franzen, L. A. (1978) Experimental ultrasonically induced lesions in the retina, choroid and sclera. Invest. Ophthalmol. 17 350.
67. Markham, D. E. & Wood, M. R. (1980) Ultrasound for Dupuytren's contracture. Physiotherapy 66 55—58.
68. Middlemast, S., & Chatterjee, D. S. (1978) Comparison of ultrasound and thermotherapy for soft tissue injuries. Physiotherapy 64 331—332.
69. Morton, К. I., ter Haar, G. R., Stratford, I. J., & Hill, C. R. (1983) Subharmonic emission as an indicator of ultrasonically induced biological damage. Ultrasound in Med. & Biol. 9 629—633.
70. O'Neil, H. T. (1949) Theory of focusing radiators. J. acoust. Soc. Am. 21 516—526.
71. Patrick, M. K. (1973) Ultrasonic therapy — has it a place in the 70's? Physiotherapy 59 282—283.
72. Paul, W. D., & Imig, C. J. (1955) Temperature and blood flow studies after ultrasonic irradiation. Am. J. Phys. Med. 34 370—375.
73. Pond, J. B. (1970) The role of heat in the production of ultrasonic focal lesions. J. acoust. Soc. Am. 47 1607—1611.
74. Pospisilova, J. (1976) Effect of ultrasound on collagen synthesis and deposition in experimental granuloma tissue. Acta Chir. Plast. (Praha) 18 176—183.
75. Pospisilova, J., Brazdova, K., & Velecky, R. (1974) Effect of ultrasound multiplied by non-pathogenic infection on collagen tissue formation. Experientia 30 755—757.
76. Pospisilova, J., Samohyl, J., Koprivova, M., & Jelinkova, A. (1980) Our experience with the use of ultrasound in rehabilitation of hand. Acta Chir. Plast. {Praha) 22 191—199.
77. Repacholi, M. H., & Benwell, D. A. (1979) Using surveys of ultrasound therapy devices to draft performance standards. Health Physics 36 679—686.
78. Robinson, Т. C, & Lele, P. P. (1972) An analysis of lesion development in the brain and in plastics by high intensity focused ultrasound at low megahertz frequencies. J. acoust. Soc. Am. 51 1333—1351.
79. Rubin, D., & Kuitert, J. H. (1955) Use of ultrasonic vibration in the treatment of pain arising from phantom limbs, scars and neuromas: A preliminary report. Arch Phys. Med. Rehab. 35 445—452.
80. Shotton, К. C. {1980) A tethered float radiometer for measuring the power from ultrasonic therapy equipment. Ultrasound in Med. and Biol. 6 131—133.
81. Sjoberg, A., Stable, J., Johnson, S., & Sahl, R. (1963) Treatment of Meniere's disease by ultrasonic irradiation. Acta Oto-laryngolica. Suppl. 178.
82. Sorensen, H., Andersen, M. S. (1979) Long term results of ultrasonic irradiation in Meniere's disease. Clinical Otolaryngology 4 125—129.
83. Stewart, H. F., Harris, G. Herman, B. A., Robinson, R. A., Haran, M. E., McGall, G. R., Carless, G., & Rees, D. (1974) Survey of use and performance of ultrasonic equipment in Pinellas county, Florida. Phys. Therapy 54 707—715.
84. Summer, W., Patrick, M. K. (1964) Ultrasonic therapy - a textbook for physiotherapists. Elsevier, London.
85. Suppipat, N. (1974) Ultrasonics in periodontics. J. Clin. Periodont 1 206—213
86. Szent-Gyorgi, A. (1933) Chemical and biological effects of ultrasonic radiation Nature 131 278.
87. Warren, C. G., Koblanski, J. N.. & Sigelmann, R. A. (1976) Ultrasound coupling media: their relative transmissivity. Arch Phys. Med. Rehab 57 218—222
88. Warwick, R., & Pond, J. B. (1968) Trackless lesions in nervous tissues produced by high intensity focused ultrasound (high frequency mechanical waves) /. Anat. 102 387—405.
89. Webster, D. E, Dyson, M., & Ha/vey, W. (1979) Ultrasonically induced stimulation of collagen synthesis in vivo. Proc. 4th Eur. Symp. on Ultrasound in Biology and Medicine. 1 135—140.
90. Webster, D. F., Harvey, W, Dyson, M., & Pond, J. B. (1980) The role of ultrasound-induced cavitation in the in vitro stimulation of collagen synthesis in human fibroblasts. Ultrasonics 18 33—37.
91. Webster, D. E, Pond, J. D., Dyson, M., & Harvey, W (1978) The role of cavitation in the in vitro stimulation of protein synthesis in human fibroblasts by ultrasound. Ultrasound in Med. & Biol. 4 343—351
92. Wells, P.N. Т., Bullen, M. A., Follett, D. M., Freundlich, H. F., & James, LA. (1963) The dosimetry of small ultrasonic beams. Ultrasonics 1 106—110
93. Witcofski, R. L., Kremkau, F. W. (1978) Ultrasonic enhancement of cancer radiotherapy. Radiology 27 793—797
94. Woeber, К (1957) Diminution of X-ray dosage in cancer by simultaneous X-ray and ultrasound treatment (Biological basis and clinical results). Acta dermat venereol. Proc. Uth Internal. Congr. Dermat. Vol. 2 pp 434-436
95. Woeber, K. (1965) The effect of ultrasound in the treatment of cancer. In- Ultrasonic energy, ed. E. Kelly. Univ. of Illinois Press, Urbana. Ch 9 pp 137-149
96. Woolley, P. E., Barnett, R. J., & Pond, J. B. (1975) The use of probes to measure megahertz ultrasonic fields in liquids. Ultrasonics 13 68—72.
97. Zinner, D. D. (1955) Recent ultrasonic dental studies, including periodentia, without the use of an abrasive. J. Dental Researsh 34 748—749.
ОЦЕНКА БЕЗОПАСНОСТИ ПРИМЕНЕНИЯ УЛЬТРАЗВУКА В МЕДИЦИНЕ
Г. тер Хаар
Как научные, так и профессиональные интересы обязывают ученых выяснить, какую опасность для пациента и оператора представляет использование ультразвука, аналогично тому, как это делается в случае других физических полей, передающих энергию в тело человека. Такие исследования идут с первых дней применения ультразвука как в терапии, так и в диагностике, и поскольку абсолютных доказательств безопасности любого данного метода быть не может, эта тема, вероятно, будет постоянным предметом споров и обсуждений.
Цель главы — рассмотреть различные аргументы, которые можно привлечь для решения вопроса. При этом будет необходимо обсудить не только соответствующие биологические аспекты, но и сами понятия «безопасность» и «риск» в контексте как терапевтической, так и диагностической практики. Мы сделаем также обзор некоторых указаний и рекомендаций, подготовленных различными группами экспертов, в том числе и международными.
Ниже мы сначала попробуем несколько продвинуть обсуждение (см. разд. 3.8) методов измерений ультразвуковых экспозиций в медицинской практике. Затем рассмотрим биологические результаты, причем это будет удобно сделать в порядке возрастания сложности в организации объектов.
14.2. ПРАКТИКА И УРОВНИ ОБЛУЧЕНИЯ
Величину экспозиции для тканей человека, подвергающихся облучению при использовании ультразвукового медицинского оборудования, оценить сложно. Параметры на выходе аппаратуры обычно измеряются в водяной ванне в условиях свободного поля. Для полного описания ультразвукового поля требуется много параметров. Они могут включать частоту, размеры излучателя, коэффициент заполнения при импульсном режиме, среднюю по времени мощность, пространственную и временную пиковые интенсивности.
Эти параметры и их определения обсуждались в разд. 3.8.
Характерные величины параметров облучения для различных типов медицинских ультразвуковых приборов показаны в табл. 14.1. Разумеется, это не полный список, но он дает величины для сравнения.
Во время ультразвукового облучения энергия передается в ткань через какую-либо контактную среду. Для большинства диагностических исследований контакт осуществляется с помощью геля, который намазывают на поверхность кожи. В случае неудобных геометрий либо облучаемый объект погружается в ванну с дегазированной водой, либо к коже прикладывается мягкий мешок с водой, сглаживающий неровности поверхности.
Контактное сканирование неизбежно приводит к облучению тканей областью ближнего поля преобразователя. В этой области имеются резкие максимумы интенсивности, особенно при непрерывном излучении, и если пучок не перемещается постоянно или прерывисто, то могут быть получены высокие дозы облучения. Чтобы избежать эффектов ближнего поля, к поверхности преобразователя иногда присоединяют удлинительную трубу, наполненную контактным веществом.
В научных публикациях стало хорошей практикой описывать уровни ультразвуковых экспозиций при изучении биоэффектов посредством усредненных по пространству и по времени интенсивностей, измеренных в условиях свободного поля в точке расположения биологического образца, а когда возможно, представлять детали профиля пучка в этой точке и величины пиковых по пространству и времени интенсивностей. Пока все это не обеспечивает полного описания поля, но позволяет сделать его разумную оценку. Ранее уже указывалось (см. разд. 3.8), что пока невозможно выделить какой-либо количественный показатель биологической эффективности ультразвука, подобно тому, как в биологии ионизирующего излучения для этой цели служит показатель поглощенной дозы. Использование интенсивности ультразвука в этом смысле необоснованно, так как ее значение обычно не связано однозначно с биологическими эффектами. В особенности это стало очевидным из обсуждений в гл. 12 того факта, что акустическое давление может быть более адекватным параметром в некоторых случаях, особенно когда возникает кавитация. Любопытно, что в публикациях такого рода редко сообщается об акустических давлениях, хотя оно часто измеряется, например, гидрофонами. Соотношение ![]() , хотя оно справедливо лишь для условий плоской бегущей волны (см.разд. 1.3.4), может быть полезным приближением во многих ситуациях.
, хотя оно справедливо лишь для условий плоской бегущей волны (см.разд. 1.3.4), может быть полезным приближением во многих ситуациях.
|
Частотный диапазон, МГц |
Коэффициент заполнения |
Интенсивность, Вт/см2 SPTP |
Максимальная амплитуда акустического давления, атм (105 Па) | |||
|
0,001 1 0,01 - 1 1 0,2 | ||||||
Хотя наилучшие работы по исследованию биоэффектов содержат точные описания условий ультразвукового облучения, однако поглощенная доза еще не может быть количественно охарактеризована. Более того, из-за влияний поглощения, рассеяния и отражения условие облучения в свободном поле может не быть в точности соблюдено при облучении биологического образца in situ даже в лабораторном эксперименте.
14.3. ИССЛЕДОВАНИЯ НА ИЗОЛИРОВАННЫХ КЛЕТКАХ
Исследование на изолированных клетках в культуре может дать полезную информацию на фундаментальном уровне об изменениях, вызванных ультразвуком в строго определенных условиях облучения. В оптимальных условиях клетки должны содержаться в таком контейнере, который как можно меньше возмущал бы ультразвуковое поле.
В рамках данной главы невозможно процитировать все доказательства изменений в клетках, вызванных ультразвуком. Вместо этого будут представлены некоторые примеры, взятые из работ на клетках млекопитающих.
Имеется множество явлений, которые используются при исследовании воздействий внешних факторов на клетки. Их можно разделить на грубые эффекты, такие, как лизис, подавление репродуктивных способностей, разрушение клеточной ультраструктуры, и более тонкие эффекты, такие, как изменение характера роста, хромосомные и функциональные изменения.
Свидетельства того, что облучение ультразвуком клеток в суспензии приводит к их лизису, многочисленны и несомненны. Показано, что кавитация является основной причиной полного разрушения клеток, и по этому поводу опубликовано уже большое число работ (см., например, [33, 46]). Неясно, однако, как ультразвук может вызывать лизис клеток в отсутствие кавитационных эффектов. Лизис, если он происходит, возникает сразу же в результате ультразвукового облучения, без временной задержки; при этом наибольшей чувствительностью обладают клетки, находящиеся в стадии митоза [7].
14.3.2. РЕПРОДУКТИВНАЯ СПОСОБНОСТЬ
Мерой биологических эффектов, общепринятой в радиобиологии, является проба клонированием. Она позволяет оценить способность клетки делиться и давать жизнеспособное потомство после воздействия.
В общем, клетки, которые пережили воздействие ультразвука и остались неповрежденными, продолжают давать потомство точно так же, как и их необлученные двойники [4, 46]. Исключение, как оказалось, составляли клетки, которые облучались ультразвуком при повышенной температуре [21, 38]. Было установлено, что потери репродуктивных свойств этими клетками выше, чем у клеток, подвергавшихся только нагреву. Механизм этого эффекта неясен, но, по-видимому, он нетепловой и некавитационный по своей природе [47].
14.3.3. ИЗМЕНЕНИЯ УЛЬТРАСТРУКТУРЫ КЛЕТОК
Были изучены многие аспекты воздействия ультразвука на клеточную ультраструктуру. Обнаружилось множество изменений; некоторые из них не обязательно вызывали гибель клеток.
Изменения в наружных клеточных мембранах, вызванные ультразвуковым облучением, обычно проявляются в изменениях ионной проницаемости мембран. Примером может служить обратимое изменение проницаемости плазматических мембран клеток вилочко-вой железы, приводящее к уменьшению содержания калия в клетке под действием ультразвука интенсивностью 1 Вт/см2 и частотой 1,8 МГц in vitro [6].
Исследования в электронном микроскопе клеток, облученных ультразвуком терапевтической интенсивности, выявили повреждения различных органелл и, в первую очередь, митохондрий. При ультразвуковом воздействии на ткани были отмечены повреждения лизосом с последующим освобождением лизосомальных ферментов. Неясно, являются ли повреждения лизосом прямым или косвенным результатом воздействия ультразвука [9, 30, 63].
Повреждение цитоплазматической мембраны с облученной стороны эндотелия кровеносных сосудов под действием поля стоячих волн было отмечено как в куриных эмбрионах, так и в сосудах матки мышей [11, 20].
Когда к механизмам воздействия добавляется кавитация, то наблюдаются не только повреждения мембран и митохондрий, но и растяжения и некоторые повреждения ретикулоэндотелиальной сети [27].
По-видимому, ядра клеток относительно мало подвержены действию ультразвука: единственный вид повреждений, замеченный в эксперименте, — это щелевидные вакуоли на ядерных мембранах [20]. В работе [65] было сделано предположение, что внутри клеток могут образовываться кавитационные пузырьки и что мембраны ядер митохондрий и гранулярной эндоплазматической сети могут играть роль кавитационных зародышей. Если бы ультразвуком подействовали на изолированные органеллы, то наблюдаемый эффект можно было бы объяснить повреждением их мембран.
14.3.4. ДНК И ГЕНЕТИЧЕСКИЕ ЭФФЕКТЫ
Ультразвук достаточно высокой интенсивности может привести к деградации ДНК в растворе. Это явление обусловлено кавитацией, а повреждения — гидродинамическими сдвиговыми напряжениями, образованием свободных радикалов или чрезмерным нагревом [64]. Маловероятно, чтобы это было возможно в условиях медицинских ультразвуковых экспозиций.
Многочисленные исследования посвящены изучению хромосомных изменений и обмена сестринскими хроматидами под действием ультразвука. И было показано, что ультразвук даже достаточно высокой интенсивности (100 Вт/см2 SPTP) не вызывает повреждений хромосом (исчерпывающий обзор см. [55]). Показано, однако, что хромосомные аберрации могли возникать, когда за рентгеновским облучением в дозе 100 рад = 1 Грей следовало воздействие ультразвуком интенсивностью 3 Вт/см2 и частотой 810 кГц, но не в случае обратной последовательности [35].
Анализ обмена сестринскими хроматидами (SCE) часто применяется в качестве средства для исследования воздействия потенциально мутагенных агентов на клетки млекопитающих, хотя связь выводов для отдельной клетки и для целого организма пока плохо понята [17, 36]. Сообщение, что диагностический ультразвук может вызывать SCE in vitro [39] стимулировало взрыв публикаций на эту тему, некоторые из них обобщены в табл. 14.2, причем в большинстве работ показано, что результат воздействия отрицательный даже при интенсивностях вплоть до 3 Вт/см2 (3,15 МГц в режиме непрерывного излучения).
Известно, однако, одно сообщение о том, что ультразвук может вызывать разрушения хромосом, но это сообщение не подтверждено независимыми исследованиями в других лабораториях, а в большинстве опубликованных и тщательно документированных работ хромосомные аберрации под действием ультразвука не наблюдались. Следует отметить, что эти исследования проведены в основном in vitro, когда механизмы воздействия совсем необязательно те же, что и в тканях in vivo.
Таблица 14.2. Обмен сестринскими хроматидами, вызванный ультразвуком*
|
Тип клеток |
Параметры ультразвука |
Результат |
Литература |
|
Лейкоциты человека |
Непрерывный |
Отрицательный |
[50] |
|
in vitro |
15,3—36 Вт/см2 SP |
|
|
|
Лимфоциты человека |
Импульсный |
Положительный |
[39] |
|
in vitro |
2,7 Вт/см2 SATA |
|
|
|
HeLa |
Импульсный |
Отрицательный |
[40] |
|
in vitro |
35,4 Вт/см2 SPTP 6,6 Вт/см2 SATA |
|
|
|
CHO(G2) |
Импульсный |
То же |
[67] |
|
in vitro |
10 мВт/см2 SPTA |
|
|
|
Лимфоциты человека |
Импульсный |
Положительный |
[26] |
|
in vitro |
1,3 Вт/см2 SPTP 0,02 мВт/см2 SPTA |
|
|
|
Амниотические клетки |
Импульсный |
Отрицательный |
[75] |
|
in vivo |
|
|
|
|
Лимфоциты человека |
Импульсный |
Положительный |
[15] |
|
in vivo |
|
|
|
|
Фибробласты |
Непрерывный |
Отрицательный |
[2] |
|
in vitro |
3 Вт/см2 SP |
|
|
|
CHO(Gi, S) |
Импульсный |
То же |
[68] |
|
in vitro |
0,01 Вт/см2 SPTP |
|
|
|
Амниотические клетки |
Импульсный |
» |
[43] |
|
in vivo |
5 мВт/см2 SATP |
|
|
|
Костный мозг |
Непрерывный |
|
[1] |
|
in vivo |
0,3—0,6 Вт/см2 SP |
|
|
*Обзор по этому вопросу опубликован Миллером [49].
14.3.5. ФУНКЦИОНАЛЬНЫЕ ИЗМЕНЕНИЯ
Ультразвук может стимулировать или подавлять функции клеток. Пример его стимулирующего действия — увеличение синтеза белка при облучении фибробластов человека in vitro (см. разд. 13.3.2.1).
Большинство функциональных изменений обусловлены взаимодействием на уровне внешней мембраны клеток. Известно, например, что ультразвук может воздействовать на электрофоретическую подвижность клеток [62]. Это отражает изменение плотности поверхностного электрического заряда клетки (возможно, из-за изменения ее объема [51]), наблюдавшееся in vitro при кавитации, вызывающей лизис клеток [32].
Периодическое микрофотографическое исследование клеточной подвижности показывает, что вызванные ультразвуком изменения могут сохраняться в нескольких поколениях [41]. Значение этого факта для экспериментов по воздействию ультразвука in vivo далеко не ясно.
14.4. ИССЛЕДОВАНИЯ НА МНОГОКЛЕТОЧНЫХ ОРГАНИЗМАХ
Исследования биологических эффектов ультразвука проводились на самых разных многоклеточных — растениях, насекомых, мелких животных и человеке. Здесь, однако, будут обсуждены работы, проведенные только на млекопитающих.
14.4.1. ЭФФЕКТЫ В КОСТЯХ И МЯГКИХ ТКАНЯХ
Вопрос о риске, возникающем при облучении костей и тканей взрослого организма весьма непрост, поскольку во многих случаях, например в физиотерапии, необходимы управляемые биологические изменения, и, как уже подчеркивалось раньше, эти изменения не должны быть опасными.
а) Эффекты в костях
Влияние кости, расположенной внутри мягкой ткани, на поглощение ультразвука уже обсуждалось в гл. 12. Вероятно главным эффектом, возникающим в кости, является нагрев ее надкостницы, поскольку из-за слишком большого поглощения ультразвуковой энергии в кости ультразвук не проникает в нее глубоко на частотах, применяемых в медицине.
Удивительно мало изучено влияние ультразвука на кость [13, 18]. Дайсон с сотр. показали, что ультразвуковое облучение места перелома полезно во время воспалительной или ранней пролиферационной фазы выздоровления, но, поскольку стимулирует рост хрящей, вредно в поздней пролиферационной фазе. Голдблат [18] сообщил, что перелом начинает срастаться быстрее сразу после облучения, но затем эффект уменьшается и через 6—7 недель сросшаяся после ультразвукового воздействия кость не прочнее контрольного образца.
Барт и Вахсман [3] рассмотрели влияние ультразвука на кости собак разного возраста как при стационарном положении преобразователя, так и при его перемещении. Оказалось, что в молодых костях возникает утолщение, которое сопровождается потерей надкостницы. Пороговая интенсивность в режиме стационарного преобразователя была в пределах 0,5—1 Вт/см2. Подобные эффекты наблюдались и в старых костях, но развивались они дольше. Эти изменения обусловлены, по-видимому, нагревом надкостницы.
Наиболее вероятно, что главной проблемой при облучении костей будет нагрев надкостницы. Не исключено, что это и будет ограничивающим фактором в физиотерапии или гипертермических методах лечения в участках, где кости расположены близко к поверхности. У человека с нормальной чувствительностью чрезмерный нагрев надкостницы, вероятно, приведет к ощущению боли (см., например, [37]), и если процедуру облучения прервать при возникновении боли, то, вероятно, можно избежать повреждений. Особое внимание надо проявлять к пациентам с пониженной чувствительностью к боли, т. е. не имеющим подобной «системы предупреждения ».
б) Эффекты в мягких тканях
Изменения ультраструктуры, вызываемые ультразвуком в неповрежденных тканях in vivo, уже обсуждались (см. разд. 14.3.1). Обобщая, можно сказать, что наиболее часто подвергаются воздействию внешние мембраны клеток, лизосомы и митохондрии.
Эффекты в мягких тканях были исследованы из-за растущего интереса к использованию ультразвука в физиотерапии. Ускорение заживления ран [12] и стимуляция регенерации тканей [10] уже обсуждались в разд. 13.3.2.1.
Когда гладкие мышцы млекопитающих облучаются ультразвуком, наблюдаются самые разнообразные эффекты — от изменения силы сокращений [19, 61] до уменьшения потенциала действия [31]. Эти эффекты наблюдаются при интенсивностях выше 1Вт/см2 и, как считают, обусловлены изменениями в транспорте ионов через клеточные мембраны, вызываемыми акустическими микропотоками.
14.4.2. ВОЗДЕЙСТВИЕ НА КРОВЬ И КРОВЕНОСНЫЕ СОСУДЫ
Эритроциты являются компонентом крови, наименее чувствительным к повреждающему действию ультразвука. Считается, что гемолиз вызывается или кавитацией, или высокими гидродинамическими напряжениями [54, 70]. Есть, однако, некоторые признаки того, что гемолиз может происходить при терапевтических интенсивностях в случае коллапсирующей кавитации и в зонах турбулентных потоков [74]. Показано также, что АТФ может высвобождаться при низких средних по пространству интенсивностях, если эритроциты облучаются in vitro в присутствии стабильных газовых полостей [73].
Наиболее чувствительным компонентом крови являются тромбоциты. Независимо от места, где возникает гемолиз, повреждение тромбоцитов из-за возможного образования тромбов может привести к значительному риску.
Вильяме [71] показал in vitro, что повреждения тромбоцитов могут происходить из-за сдвиговых напряжений в окружающей жидкости существенно меньших тех, которые требуются для повреждения эритроцитов и других компонентов крови. Таким образом, при введении в суспензию тромбоцитов стабильных пузырьков повреждения могут быть замечены при средней по пространству интенсивности ниже 0,8 Вт/см2 [48].
Однако попытки обнаружить повреждения компонент крови при ультразвуковом облучении человека in vivo закончились неудачей [72]. Кажется маловероятным, что такие повреждения было бы легко обнаружить in vivo, поскольку малые количества поврежденных клеток быстро заменяются нормальными клетками из-за кровотока через данную область.
Показано, что облучение кровеносных сосудов в поле стоячей волны вызывает повреждения облученной стороны плазматических мембран как в сосудистой зоне эмбрионов цыплят [И], так и в сосудах матки мышей [20]. По внешнему виду и местоположению этих повреждений можно предположить, что они вызваны сдвиговыми напряжениями, обусловленными акустическими микропотоками. Когда повреждения наиболее сильны, можно заметить выход эритроцитов в окружающую ткань. Механизм повреждений связан с образованием стоячих волн, требующих определенного времени для своего развития до эффективных амплитуд. Поэтому избежать повреждений можно путем использования режимов с перемещающейся головкой ультразвукового преобразователя.
14.4.3. ПОСЛЕДСТВИЯ УЛЬТРАЗВУКОВОГО ОБЛУЧЕНИЯ ЭМБРИОНОВ
Естественен большой интерес к биологическим последствиям облучения эмбрионов в матке в основном из-за широкого использования ультразвуковых диагностических приборов в акушерстве. Были проведены исследования тератогенных и генетических эффектов, а также эволюционных изменений.
Большинство исследований проводилось на крысах и мышах. Эти эксперименты имеют множество недостатков. Сложно, например, количественно определять поле в столь мелких животных, а в большинстве экспериментов в ультразвуковой пучок попадала большая часть тела животного, в результате чего возникал нагрев всего тела.
Невозможно детально описать все исследования, проведенные на развивающихся эмбрионах, некоторые из них собраны в таб. 14.3. Оказалось, что в большинстве случаев, для которых наблюдались ненормальности в развитии зародышей, в матке возникало увеличение температуры выше 41,5°С [24, 25, 56]. Когда же не было такого роста температуры, зародыши оказывались нормальными. Лили [42] было показано, что гипертермия матки может приводить к разнообразным тератогенным эффектам, рассасыванию зародышей или задержкам их роста.
Курто с соавт. [8] нашли, что увеличенная смертность потомства мышей вызывалась облучением ультразвуком в непрерывном режиме интенсивностью 125—500 мВт/см2 SATA, 1 МГц. Эдмондс с соавт. [14] не смогли повторить эти результаты на частоте 2 МГц и интенсивности 440 мВт/см2 при различных сроках беременности. Имеется множество сообщений в литературе об уменьшении веса зародышей из-за облучения ультразвуком в матке [53, 59, 60].
Большинство из этих исследований было проведено на стадии формирования органов зародыша (около 8 дней для мышей, 9 дней для крыс). Несмотря на это, никаких существенных эффектов не было отмечено при интенсивностях, используемых в диагностике (см. табл. 14.3). Как свидетельствуют факты, маловероятно, чтобы применение ультразвуковой диагностической аппаратуры в акушерстве давало бы какое-либо увеличение тератогенных эффектов или аномалий развития. Кроме того, условия облучения экспериментальных мышей и крыс значительно отличаются от условий облучения людей. В экспериментах с грызунами ультразвуковой пучок шире размеров зародышей, тогда как в случае зародыша человека на стадии его наиболее частого исследования это не так. Маловероятно, что ультразвуковая аппаратура для диагностики человека дает значительное увеличение температуры.
|
Таблица 14.3. Последствия ультразвукового облучения эмбрионов | |||||||
|
Облученная |
Условия облучения |
Проверяемые |
Результаты |
Литература | |||
|
биологическая |
|
биологические |
|
| |||
|
система |
|
показатели |
|
| |||
|
Беременные мыши, |
1—3 МГц, 5 мин, |
Количество мышей |
Заметных |
[66] | |||
|
срок беремен- |
200—490 Вт/см2 SPTP, |
в помете, скорость |
эффектов нет |
| |||
|
ности 8 дней |
0,75—27 Вт/см2 SPTA, |
рассасывания, не- |
|
| |||
|
|
импульсы |
нормальности раз- |
|
| |||
|
|
Юмкс—10 мс |
вития |
|
| |||
|
Беременные мыши |
2,25 МГц, 5 ч, |
Вес зародышей, |
Заметное |
[56] | |||
|
двух линий, |
непрерывный, |
гибель зародышей, |
влияние на |
| |||
|
срок беремен- |
40 мВт/см2 ТА |
уродства |
гибель заро- |
| |||
|
ности 8 дней |
|
|
дышей в од- |
| |||
|
|
|
|
ной линии |
| |||
|
Беременные крысы |
1,9 МГц, 10 мин, |
Жизнеспособность |
Заметных |
[16] | |||
|
|
100 Вт/см2 SATP, |
зародышей, расса- |
эффектов нет |
| |||
|
|
1 Вт/см2 SATA, |
сывание |
|
| |||
|
|
импульсы 0,6—10 мс |
|
|
| |||
|
Беременные мыши, |
1 МГц, 3 мин, |
Выживаемость по- |
Значительное |
[8] | |||
|
срок беремен- |
непрерывный, |
томства к 21 дню |
уменьшение |
| |||
|
ности 14 дней |
0,5 Вт/см2 SA |
|
выживаемо- |
| |||
|
|
|
|
сти при |
| |||
|
|
|
|
0,125 Вт/см2 |
| |||
|
Беременные мыши, |
1 МГц, SA, |
Вес зародышей |
Значительное |
[53] | |||
|
срок беремен- |
0,5—0,7 Вт/см2, 300с, |
|
уменьшение |
| |||
|
ности 8 дней |
2—3 Вт/см2, 20 с, |
|
среднего веса |
| |||
|
|
3—5,5 Вт/см2, 10 с |
|
|
| |||
|
Беременные мыши, |
2,3 МГц, 5—60 мин, |
Структурные изме- |
Заметных |
[44] | |||
|
срок беремен- |
непрерывный, |
нения, генетические |
эффектов нет |
| |||
|
ности 8 дней |
0,16—10 Вт/см2 |
уродства, хромо- |
|
| |||
|
|
|
сомные аберрации |
|
| |||
|
Беременные мыши, |
2 МГц, 5 мин, |
Вес мыши, урод- |
Уменьшение |
[24] | |||
|
срок беремен- |
50 мВт/см2 SATA, |
ства зародышей |
веса мышей, |
| |||
|
ности 8 дней |
импульсный |
|
ненормаль- |
| |||
|
|
22 Вт/см2 TP |
|
ности в раз- |
| |||
|
|
|
|
витии за- |
| |||
|
|
|
|
родышей |
| |||
|
Беременные мыши, |
2 МГц, 5 мин, |
Уродства |
Заметны |
[24] | |||
|
срок беремен- |
2 Вт/см2 |
зародышей |
ненормаль- |
| |||
|
ности 8 дней |
|
|
ности |
| |||
|
|
|
|
развития |
| |||
|
Беременные мыши, |
2МГц, непрерывный |
Вес зародышей |
Значительное |
[59] | |||
|
срок 1, 2, 4, 7, |
0,5 Вт/см2, 140 с, |
|
уменьшение |
| |||
|
13 дней |
1 Вт/см2, 60 с |
|
|
| |||
|
Облученная биологическая система |
Условия облучения |
11роверяемые биологические показатели |
результаты литература |
| |||
|
Беременные мыши |
2,3 МГц, непрерывный 80—100 мВт/см2 SATA |
Вес зародышей |
Значительное уменьшение |
[60] |
| ||
|
Беременные мыши, срок 8 дней |
2 МГц, непрерыв- SATA рожденных |
Смертность ново-ный 0,44 Вт/см2 |
Заметных эффектов нет |
[14] |
| ||
|
Беременные крысы, срок 9 дней |
3,2 МГц, непрерывный, 0,32-^ Вт/см2 SA, 15 мин |
Размеры зародышей и уродства |
Заметных эффектов нет до 3 Вт/см2 |
[57] |
| ||
|
Беременные крысы, срок 8, 9, 10, 11, 12, 13 дней |
2,5 МГц, непрерывный, 10 мВт/см2 1,5—2 ч SA |
Численность помета, степень рассасывания, вес зародышей |
Заметных эффектов нет |
[45] |
| ||
14.4.4. УЛЬТРАЗВУК В ОНКОЛОГИИ
Возможности ультразвука в онкологии обсуждались в разд. 13.5. Основной целью его применения было нагреть ткани опухоли до температур, используемых в гипертермии (42—45°С), сохраняя при этом нормальные ткани при обычной температуре. Потенциальная опасность такого применения связана с возможностью нанести вред нормальным тканям, окружающим опухоль, или разнести по организму злокачественные клетки, провоцируя тем самым метастазирование.
Точная локализация акустического пучка должна минимизировать риск для нормальных тканей. Кроме того, нормальная мышечная ткань реагирует на повышение температуры увеличением кровотока, вызывая охлаждение ткани (см., например, [22]). Неясно только, действует ли такой механизм охлаждения и в опухолях.
Вопрос, может или нет гипертермия увеличить скорость метастазирования опухоли, пока далек от своего решения. Общая гипертермия мышей может увеличить скорость метастазирования, но нет фактов, подтверждающих, что локальный нагрев как-то влияет на возникновение метастазов [23]. Смахло с сотр. [58] провели исследования на фибросаркоме у хомячков, используя ультразвук с частотой 5 МГц и интенсивностью 3 Вт/см2 SATA, и не обнаружили увеличения метастазирования.
Таким образом, осторожное использование ультразвука для лечения рака, по-видимому, не опасно, если опухоль не располагается непосредственно на кости. В этих случаях возможна ситуация, когда интенсивности ультразвука, необходимые для адекватного воздействия на опухоль, вызовут значительный нагрев надкостницы и сильные болевые ощущения. Последнее, как показал опыт, может быть одним из ограничивающих факторов при лечении некоторых пациентов.
14.5. ИССЛЕДОВАНИЯ ЭМБРИОНОВ ЧЕЛОВЕКА
Поскольку ультразвук в акушерстве используется давно и широко, то весьма вероятно, что какие-либо неслучайные детерминированные эффекты, которые могли возникнуть при облучении ультразвуком, были бы обнаружены и описаны к настоящему времени. Однако, чтобы обнаружить любые редкие стохастические эффекты, обусловленные действием ультразвука на эмбрионы и отделить их от спонтанных или обусловленных другими факторами явлений, необходимо проведение крупномасштабных эпидемиологических исследований. В литературе сообщений об исследованиях такого рода нет, очевидно, из-за их большой стоимости и продолжительности.
Однако, опубликован, например, ретроспективный обзор [28] обследований 1114 нормальных беременных женщин на различных стадиях беременности. Для группы женщин, обследованных с помощью ультразвука, было отмечено 2,7% случаев врожденных не-нормальностей эмбрионов, в то время как в контрольной группе их было 4,8%.
Впоследствии было дополнительно опубликовано около десятка статей, посвященных этим исследованиям, где поиск изменений вели в широком диапазоне признаков (см. обзор [52]). Только в одной работе была найдена значительная разница между случаями с воздействием ультразвука и без него. Была обнаружена связь между облучением и уменьшением веса новорожденных, но разница могла быть обусловлена процедурой отбора пациенток для облучения по каким-либо медицинским показаниям. Несколько отличный и потенциально ценный подход к подобным обследованиям продемонстрирован в двух четко регламентированных исследованиях [5, 34].
В них спец- изучались особенности развития рака у детей, которые прошли в свое время ультразвуковое обследование. Результаты и в этом случае были отрицательными.
14.6. КРАТКИЕ РЕКОМЕНДАЦИИ И УКАЗАНИЯ ПО РЕЖИМАМ ОБЛУЧЕНИЯ
Из фактов, приведенных в данной главе и гл. 12 и 13, становится ясным, что и в условиях эксперимента, и в клинике ультразвук может вызвать множество биологических эффектов. Хотя в принципе любые биологические изменения не в той области, где их вызывают, могут быть небезопасными, с практической точки зрения полезно сосредоточить внимание на тех потенциальных эффектах, которые могут приводить к серьезной опасности, например, заболевание раком или возникновение генетических уродств, особенно если она проявляется с определенной вероятностью и, возможно, с значительным скрытым периодом. Может быть сделано, однако, следующее утверждение:
1. Лечение ультразвуком должно назначаться квалифицированными специалистами (например, опытными физиотерапевтами) и с осторожностью. Следует избегать образования стоячих волн в области кровеносных сосудов, а также проявлять осторожность при облучении газовых включений или костей, чтобы не вызвать чрезмерного нагрева.
2. Нет никаких свидетельств, что применение ультразвука в современной клинической диагностике вызывает повреждения эмбрионов человека при внутриутробном развитии. Не обнаружено хромосомных аберраций ни в материнских, ни в зародышевых лимфоцитах вследствие облучения ультразвуком.
3. Риск не возрастает при осторожном использовании ультразвука для локального нагрева при терапии рака. Нет свидетельств, что ультразвук может увеличивать степень метастазирования. Однако в этом отношении должна быть проявлена осторожность при назначении локальной гипертермии одновременно с общей гипертермией.
Многие национальные и международные группы специалистов рассматривали вопросы безопасного применения ультразвука. Вероятно, наиболее квалифицированные из них те, которые работали под эгидой Всемирной организации здравоохранения (ВОЗ) [29, 69] и Американского совета по защите от радиации и по дозиметрии [52]. Без сомнения эти группы в значительной степени влияют друг на друга, а их хорошо согласованные выводы очень полезны.
В физиотерапии имеется согласие в рекомендациях о том, что интенсивность ультразвука не должна превышать 3 Вт/см2 SATP, что не должен подвергаться облучению плод беременных женщин, и что везде, где это возможно, должен применяться режим, при котором головка преобразователя перемещается.
Что касается облучения при диагностических исследованиях, то единое мнение наилучшим образом может быть суммировано в следующих выдержках из наиболее свежего и исчерпывающего обзора [52]:
«Рабочая группа [29], собранная в 1976 г. Всемирной организацией здравоохранения, рассмотрела вопрос о необходимости введения верхнего предела интенсивности ультразвука, излучаемого диагностическими приборами, и решила не рекомендовать введение такого предела. Опубликованные комментарии рабочей группы включают также следующее: а) окончательное обоснованное заключение о соотношении риска и пользы применения ультразвука должно приниматься врачом, отвечающим за данного пациента; б) желательно препятствовать тенденции использовать более высокие интенсивности, чем это необходимо для формирования изображения; с) защитные меры не должны быть настолько ограничивающими, чтобы чрезмерно препятствовать усовершенствованию методов, а также вводить необоснованные ограничения на их использование. Как оказалось, в настоящее время многие диагностические процедуры могут быть проведены вполне успешно при условии облучения пациента пучком относительно низкой интенсивности порядка 10 мВт/см2 SATA или меньше.»
Как отмечено в обоих обзорах [52, 69], вышеприведенные утверждения частично базируются на анализе, проведенном Американским институтом по применению ультразвука в медицине. Там же установлено, что:
«В нижней области мегагерцевого диапазона частот до октября 1982 г. не было обнаружено никаких независимо подтвержденных существенных биологических эффектов в тканях млекопитающих, облученных ультразвуком интенсивностью ниже 100 мВт/см2 SPTA. Более того, при экспозиции1) от 1 до 500 с существование таких эффектов не было показано и при более высоких интенсивностях, когда произведение интенсивности (SPTA) на время экспозиции было меньше 50 Дж/см2».
1) Общее время, включая всю продолжительность импульсов и пауз в режиме повторяющихся импульсов.
Это утверждение сопровождается рядом оговорок. В частности:
а) большинство данных получено для животных, а не для человека;
б) очень мало данных для экспозиций в режиме повторяющихся коротких импульсов, а также длительных экспозиций при низких интенсивностях;
в) интенсивности, о которых сообщается как о вызывающих биоэффекты, не обязательно минимальны. Возможно, что когда биологические тесты станут более чувствительны, эти уровни необходимо будет перепроверить.
Практически количественное измерение параметров ультразвуковых воздействий часто весьма затруднительно. Не существует международной договоренности о важнейших параметрах, которые необходимо измерять, чтобы дать значимую в отношении биоэффектов характеристику излучения или экспозиции. Высказано предположение, что полезными параметрами могут быть:
1) Для эхо-импульсных приборов — пиковая по пространству амплитуда давления (сумма пиковых положительных и отрицательных значений давления) в том участке пучка, где она имеет максимальную величину (обычно вблизи фокуса). Для ситуаций, в которых этот параметр не может быть измерен, удовлетворительной альтернативой может быть максимальное значение в ультразвуковом пучке пиковой по пространству и во времени интенсивности ультразвука.
2) Для терапевтических, хирургических или доплеровских диагностических (непрерывного излучения или импульсных) приборов подобным параметром может быть общая акустическая (средняя по времени) мощность.
Для количественных измерений в экспериментах по биоэффектам эти величины должны измеряться в точках размещения образцов.
Иногда необходима специальная защита оператора от ультразвука, распространяющегося по твердым деталям или по жидкости. Должна соблюдаться осторожность в тех случаях, когда руки операторов могут погружаться в контактную промежуточную среду, как и в случае иммерсионной физиотерапии.
Вопрос о безопасности применения ультразвука в медицине имеет долгую историю и гарантированное продолжительное будущее. На многие важные вопросы невозможно найти окончательные ответы, пока время от времени возникают новые и потенциально противоречивые факты.
Вопрос о безопасности — это один из вопросов, где характерный для физики количественный подход весьма важен. Это справедливо для проблемы измерения и описания ультразвукового воздействия, но, хотя гидрофоны и сходные устройства могут быть хорошей основой для измерений, логика такого количественного подхода к метрологии терпит неудачу из-за того, что в настоящее время невозможно выделить один или даже несколько физических параметров, которые служили бы в качестве адекватных количественных характеристик, позволяющих предсказать конечный биологический эффект.
Биологическая сторона вопроса о безопасности сложна и в ряде случаев может казаться обескураживающей. Однако можно значительно упростить проблему, учитывая следующие рекомендации. Во-первых, сообщения о новых биологических явлениях должны быть четко документированы и иметь независимые подтверждения прежде, чем их всерьез принимать во внимание. Во-вторых, необходимо различать эффект (нечто наблюдаемое) и опасность (существенное вредное последствие для человека). Вероятно, следует сконцентрировать внимание на свидетельствах, касающихся мутагенеза, канцерогенеза и тератогенеза. Как уже отмечалось, накапливаются все более и более серьезные доказательства, полученные на большом числе различных биологических систем и при широком разнообразии условий ультразвукового облучения, что во всех этих трех областях каких-либо изменений не происходит. Такие доказательства должны приниматься во внимание при оценке значимости каких-либо новых и явно противоречивых сообщений.
В отсутствие адекватной информации, на основании которой должны быть установлены максимально допустимые дозы при применении ультразвука в медицине, было бы полезным выдвинуть некоторые критерии для правильного применения ультразвука. Ряд таких критериев может быть обобщен следующим образом:
1) оператор должен использовать минимальные интенсивности и экспозиции, позволяющие получить у пациента желаемый клинический эффект. Количественная сторона ультразвукового воздействия обсуждалась в разд. 14.6;
2) обслуживающий персонал не должен облучаться без необходимости;
3) все процедуры должны выполняться хорошо обученным персоналом или под его наблюдением.
Если следовать этим рекомендациям, то ультразвук можно эффективно использовать в медицине с большой уверенностью в его безопасности.
1. Au, W. W., Obergoenner, N. & Goldenthal, К. L. Соггу, Р., Willingham, V. (1982) Sister chromatid exchanges in mouse embryos after exposure to ultrasound in vitro. Mutat. Res. 103, 315.
2. Barrass, N., Ter Haar, G. R. & Casey G. (1982) The effect of ultrasound and hyperthermia on sister chromatid exchange and division kinetics of BHK21 C13/A3 cells. Brit. J. Cancer, 45 Suppl V 187.
3. Barth, G. & Wachsmann, E (1949) Biological effects of ultrasonic therapy (in German), Kongress Bericht, Erlanger Tagung 162—165.
4. Bleaney, В. I., Blackbourne, P. & Kirkley, J. (1972) Resistance of CHLF hamster cells to ultrasonic radiation of 1.5MHz frequency. Brit. J. Radiol. 45, 354—357.
5. Cartwright, R. A., McKinney, P. A., Hopton, P. A., Birch, J. M., Hartley, A. L.
Mann, J. R., Waterhouse, J. A. H., Johnston, H. E., Draper, G. J., & Stiller, C. (1984) Ultrasound examinations in pregnancy and childhood cancer. Lancet 2, 999—1000.
6. Chapman, I. V. (1974) The effect of ultrasound on the potassium contents of ratthymocytes in vitro. Brit. J. Radiol. 47, 411—415.
7. Clarke, P. R. & Hill, C. R. (1969) Biological action of ultrasound in relation to the cell cycle. Exptl Cell Res. 58, 443.
8. Curto, K. A. (1976) Early postpartum mortality following ultrasound radiation. In: Ultrasound in medicine 2, pp. 535—536 (eds. D. N. White & R. Barnes). New York, Plenum Press.
9. Dvorak, M. & Hrazdira, I. (1966) Changes in the ultrastructure of bone marrow cells in rats following exposure to ultrasound. Zeitschrift fur mikroskopisch-anatomische Forschung 4, 451—460.
10. Dyson, M., Pond, J. В., Joseph, J. & Warwick, R. (1968) The stimulation of tissue regeneration by means of ultrasound. Clin. Sci. 35, 273—285.
11. Dyson, M., Pond, J. В., Woodward, В., & Broadbent, J. (1974) The production of blood cell stasis and endothelial damage in the blood vessels of chick embryos treated with ultrasound in a stationary wave field. Ultrasound in Med. & Biol. 1, 133—148.
12. Dyson, M., Franks, C, & Suckling, J. (1976) Stimulation of healing of varicose ulcers by ultrasound. Ultrasonics 14, 232—236.
13. Dyson, M. & Brookes, M. (1983) Stimulation of bone repair by ultrasound. In: Ultrasound 82 (eds. R. A. Lerski, P. Morley) Pergamon Press pp. 61—66.
14. Edmonds, P. D, Stolzenberg, S. J., Torbit, C. A., Madan, S. M. & Pratt, D. (1979) Postpartum survival of mice exposed in utero to ultrasound. J. acoust. Soc. Am. 66, 590—593.
15. Ehlinger, C. A., Katayama, K. P., Roeler, M. R. & Mattingly, R. F. (1981) Diagnostic ultrasound increases sister chromatied exchange; preliminary report. Wisconsin Med. J. 80, 21.
16. Garrison, В. M, Walter, J., Krueger, W. A., Kremkau, F. W. & McKinney, W. M. (1973) The influence of ovarian sonication on fetal development in the rat. J. Clin U-S. 1, 316—319.
17. Gebhart, E. (1981) Sister chromatid exchange (SCE) and structural chromosome aberration in mutagenicity testing. Human Genetics 58, 235—254.
18. Goldblat, V. I. (1969) (Processes of bone tissue regeneration under the effect of ultrasound) (in Russian) Ortoped. Travmoto. Proteziro, 30, 57—61.
19. ter Haar, G. R., Dyson, M. & Talbert, D. (1978) Ultrasonically induced contractions in mouse uterine smooth muscle in vivo. Ultrasonics, 16, 275—276.
20. ter Haar, G. R., Dyson, M. & Smith, S. P. (1979) Ultrastucture changes in the mouse uterus brought about by ultrasonic irradiation at therapeutic intensities in standing wave fields. Ultrasound in Med. & Biol. 5, 167—179.
21. ter Haar, G. R., Stratford, I. J. & Hill, C. R. (1980) Ultrasonic irradiation of mammalian cells in vitro at hyperthermic temperatures. Brit. J. Radiol. 53, 784—789.
22. ter Haar, G. R. & Hopewell, J. W. (1983) The induction of hyperthermia by ultrasound: its value and associated problems. I. single, static, plane transducer. Phys. Med. & Biol. 28, 889—896.
23. Hahn, G. M. (1982) Hyperthermia and cancer Plenum Press, New York, ISBN 0-306-40958-5.
24. Нага, K., Minoura, S., Okai, T. & Sakamoto, S. (1977) Symposium on recent studies in the safety of diagnostic ultrasound, safety of ultrasonics on organism. Jpn. J. Med. Ultrasonics 4, 256—258.
25. Нага, K., (1980) Effect of ultrasonic irradiation on chromosomes, cell division and developing embryos. Acta Obst. Gynaecol. Jpn. 32, 61—68.
26. Haupt, M., Martin, A. O., Simpson, J. L., Iqbal, M. A., Elias, S., Dyer, A, & Sabbagha, R. E. (1981) Ultrasonic induction of sister chromatid exchanges in human lymphocytes. Human Genet 59, 221.
27. Harvey, W., Dyson, M., Pond, J. B. & Grahame, R. (1975) The in vitro stimulation of protein synthesis in human fibroblasts by therapeutic levels of ultrasound. In: Ultrasonics in medicine, (eds. Kazner E. et al.) pp. 10—21, Amsterdam, Exerpta Medica, (Excerpta Medica, International Congress, Series No. 363).
28. Hellman, L. M., Duffus, G. M., Donald, I. & Sunden, B. (1970) Safety of diagnostic ultrasound in obstetrics Lancet 1 1133.
29. Hill, C. R. & ter Haar, G. R. (1982) Ultrasound; Chapter 6 of Non-ionizing radiation protection, (ed. M. J. Suess). WHO Regional Office for Europe, Copenhagen, European Series of Publications # 10 pp. 199—228. (Revised edition is in press).
30. Hrazdira, I. (1970) Changes in cell ultrastructure under direct and indirect action of ultrasound. In: Ultrasonographia medica, Vienna, (eds: Bock, J. & Ossoinig, K.) Vienna Academy of Medicine, pp. 457—463.
31. Hu, J. H., Taylor, J. D., Press, H. C. & White, J. E. (1978) Ultrasonic effects on mammalian interstitial muscle membrane. Aviat. Space Environ. Med. 49, 607—609.
32. Joshi, G. P., Hill, C. R. & Forrester, J. A. (1973) Mode of action of ultrasound on the surface charge of mammalian cells. Ultrasound in Med. & Biol. 1, 45—48.
33. Kaufman, G. E., Miller, M. W., Griffiths, T. D. & Ciaravino, V. (1977) Lysis and viability of cultured mammalian cells exposed to 1 MHz ultrasound. Ultrasound in Med. & Biol. 3, 21—25.
34. Kinnier Wilson, L. M. & Waterhouse, J. A. H. (1984) Obstetric ultrasound and childhood malignancies. Lancet 2, 997—998.
35. Kiinze-Muhl, E. (1981) Observations on the effect of X-ray alone and in combination with ultrasound on human chromosomes. Human Genetics 57, 257—260.
36. Latt, S. A. & Schreck, R. R. (1980) Sister chromatid exchange analysis. Am. J. Hum. Genet. 32, 297.
37. Lehmann, J. F., DeLateur, B. J., Stonebridge, J. B. & Warren, C. G. (1967) Therapeutic temperature distribution produced by ultrasound as modified by dosage and volume of tissue exposed. Arch. Phys. Med. & Rehab. 48, 662—666.
38. Li, G. C, Hahn, G. M. & Tolmach, L. J. (1977) Cellular inactivation by ultrasound. Nature 267, 163—165.
39. Liebeskind, D., Bases, R., Mendez, F., Elequin, F. & Koenigsberg, M., (1979) Sister chromatid exchanges in human lymphocytes after exposure to diagnostic ultrasound. Science, 205, 1274—1275.
40. Liebeskind, D., Bases, R., Eliequin, F., Neubort, S., Leifer R., Goldberg, R. & Koenigsberg, M. (1979) Diagnostic ultrasound: Effects on DNA and growth patterns of animal cells. Radiology 131, 177—184.
41. Liebeskind, D., Padawer, J., Wolley, R. & Bases, R. (1982) Diagnostic ultrasound: time lapse and transmission electron microscopic studies of cells insonated in vitro. Br. J. Cancer 45, Suppl. V, 176—186.
42. Lele, P. P. (1979) Safety and potential hazards in the current applications of ultrasound in obstetrics and gynaecology. Ultrasound in Med. & Biol. 5, 307—320.
43. Lundberg, M., Jerominski, L., Livingston, G., Kochenour, N., Lee, T. & Fineman, R. (1982) Failure to demonstrate an effect of in vivo diagnostic ultrasound on sister chromatid exchange frequency in anniotic fluid cells. Amer. J. Med. Genet. 11, 31.
44. Mannor, S. M., Serr, D. M., Tamari, I., Meshorer, A. & Frei, E. H. (1972) The safety of ultrasound in fetal monitoring. Am. J. Obstet. Gynaecol. 113, 653—661.
45. McClain, R. M., Hoar, R. M. & Saltzman, M. B. (1972) Teratological study of rats exposed to ultrasound. Am. J. Obstet. Gynaecol. 114, 39—42.
46. Morton, К. I., ter Haar, G. R., Stratford, I. J. & Hill, C. R. (1982) The role of cavitation in the interaction of ultrasound with V79 Chinese Hamster cells in vitro. Br. J. Cancer 45, 147—150.
47. Morton, К. I., ter Haar, G. R., Stratford, I. J. & Hill, C. R. (1983) Subharmonic emission as an indicator of ultrasonically induced biological damage. Ultrasound in Med. & Biol. 9, 629—633.
48. Miller, D. L., Nyborg, W. L. & Whitcomb, С. C. (1979) Platelet aggregation induced by ultrasound under specialized conditions in vitro. Science 205, 505—507.
49. Miller, M. W. (1985) Does ultrasound induce sister chromatid exchanges? Ultrasound in Med. Biol., 11, 561—570.
50. Morris, S. M., Palmer, С. C, Fry, F. J. & Johnson, L. K. (1978) Effect of ultrasound on human leucocytes in sister chromatid exchange analysis. Ultrasound in Med. & Biol., 4, 253.
51. Mummery, C. L. (1978) Effect of ultrasound on fibroblasts in vitro. PhD. thesis, University of London.
52. NCRP (1984) Biological effects of ultrasound: mechanisms and clinical implications. Report # 74. Washington B.C., National Council for Radiological Protection.
53. O'Brien, W. D. (1976) Ultrasonically induced fetal weight reduction in mice. In: Ultrasound in medicine (ed. D. N. White) New York, Plenum Press 2, pp. 531—532.
54. Rooney, J. A. (1970) Hemolysis near an ultrasonically pulsating gas bubble. Science 169, 869—871.
55. Rott, H-D. (1981) Zur Frage der Schadigungsmoglichkeit durch diagnostischen Ultraschall. Ultraschall 2, 56.
56. Shoji, R., Murackami, U. & Shimizu, T. (1975) Influence of low intensity ultrasonic irradiation on prenatal development of two inbred mouse strains. Teratology 12, 227—232.
57. Sikov, M. & Hildebrand, B. P. (1976) Effects of ultrasound on the prenatal development of the rat. Part 1: 3.2 MHz continuous wave at nine days gestation. Ultrasound 4, 357—363.
58. Smachlo, K., Fridd, C. W., Child, S. Z., Hare, J. D., Linke, C. A. & Carstensen, E. L. (1979) Ultrasonic treatment of tumors: 1. Absence of metastases following treatment of a hamster fibrosarcoma. Ultrasound in Med. & Biol. 5, 45—49.
59. Stolzenberg, S. J., Torbit, C. A., Pryor, G. T. & Edmonds, P. D. (1980) Toxicity of ultrasound in mice: neonatal studies. Radiat. environ. Biophys. 18, 37—44.
60. Tachibana, M., Tachibana, Y. & Suzuki, M. (1977) The present status of the safety of ultrasonic diagnosis in the area of obstetrics — the effect of ultrasound irradiation on pregnant mice as indicated in their fetuses. Jpn. J. Med. Ultra-son. 4, 279—283.
61. Talbert, D. G. (1975) Spontaneous smooth muscle activity as a means of detecting biological effects of ultrasound. In: Proceedings of Ultrasonics International, 1975. Guildford IPC Science & Technology Press, p. 279—284.
62. Taylor, K. J. W. & Newman, D. L. (1972) Electrophoretic mobility of Ehrlich suspensions exposed to ultrasound of varying parameters. Phys. in Med. & Biol. 17, 270—276.
63. Taylor, K. J. W. & Pond, J. B. (1972) Primary sites of ultrasonic damage on cell systems. In: Interaction of ultrasound and biological tissues, (eds. J. M. Reid & M. R. Sikov) Washington D. C. DHEW Publication No (FDA)73-8008.
64. Thacker, J. (1973) The possibility of genetic hazard from ultrasonic radiation. Current Topics in Radiation Research Quarterly 8, 235—258.
65. Watmough, D. J., Dendy, P. P., Eastwood, L. H., Gregory, D. W, Gordon, F. C. A. & Wheatley, D. N. (1977) The biophysical effects of therapeutic ultrasound in HeLa cells. Ultrasound in Med. & Biol. 3, 205—219.
66. Warwick, R., Pond, J. В., Woodward, B. & Connolly, С. C. (1970) Hazards of diagnostic ultrasonography — study with mice. IEEE Trans. Sonics. Ultrasonics. SU-17, 158—164.
67. Wegner, R.-D., Obe, G. & Meyenburg, M. (1980) Has diagnostic ultrasound mutagenic effects? Hum. Genet. 56, 95—98.
68. Wegner, R.-D. & Meyenburg, M. (1982) The effects of diagnostic ultrasonography on the frequencies of sister chromatid exchanges in Chinese hamster cells and human lymphocytes. J. Ultrasound Med. 1, 355.
69. WHO (1982) Environmental health criteria 22: Ultrasound, Geneva, World Health Organization.
70. Williams, A. R., Hughes, D. E. & Nyborg, W. L. (1970) Hemolysis near a transversely oscillating wire. Science 169, 871—873.
71. Williams, A. R. (1974) Release of serotonin from human platelets by acoustic microstreaming. J. acoust. Soc. Am. 56, 1640—1643.
72. Williams, A. R., Chater, В. V., Sanderson, J. H., Taberner, D. A., May, S. J., Allen, K. A. & Sherwood, M. R. (1977) Beta-thromboglobulin release from human platelets after in vivo ultrasound irradiation. Lancet 2, 931—932.
73. Williams, A. R. & Miller, D. L. (1980) Photometric detection of ATP release from human erythrocytes exposed to ultrasonically activated gas-filled pores. Ultrasound in Med. & Biol. 6, 251—256.
74. Wong, Y. S. & Watmough, D. J. (1980) Hemolysis of red blood cells in vitro and in vivo caused by therapeutic ultrasound at 0.75 MHz. Proc. Ultrasound interaction in Biology and Medicine Symposium, Reinhardsbrunn, GDR, November 10—14. Paper C-14.
75. Zheng, H. Z., Mitter, N. S. & Chudley, A. C. (1981) In vivo exposure to diagnostic ultrasound and in vitro assay of sister chromatid exchange in cultured amniotic fluid cells. IRCS Medical Science: Biochemistry, Biomedical Technology; Cell and Membrane Biology, Clinical Biochemistry, Developmental Biology and Medicine', Pathology, Reproduction Obstetrics and Cynecology, 9, 491.
Лккерман Ю. Биофизика. — М.: Мир, 1964. Акустическая голография.—Л.: Судостроение, 1975.
Акустические свойства биологических объектов: Тезисы докл. Междунар. симп. — Пущино: изд-во АН СССР, 1984.
Акустоскопия: Тематический выпуск. — ТИИЭР, 1979, т. 67, № 4.
Байер Я, Дернер Э. Ультразвук в биологии и медицине. — Л.: Медгиз, 1958.
Бергман Л. Ультразвук. — М.: ИЛ, 1956.
Боббер Р. Д. Гидроакустические измерения. — М.: Мир, 1974.
Богданович Л. И. Ультразвук при лечении кожных болезней. — Минск: Беларусь, 1967.
Бражников Н. И. Ультразвуковые методы.—Л.: Энергия, 1965.
Взаимодействие ультразвука с биологической средой: Тезисы докл. Всесоюзн. симп. — Пущино: изд-во АН СССР, 1979.
Взаимодействие ультразвука с биологической средой: Тезисы докл. — М.: изд-во АН СССР, 1983.
Викторов И. А. Физические основы применения ультразвуковых волн Рэлея и Лэмба в технике. — М.: Наука, 1966.
Викторов И. А. Звуковые поверхностные волны в твердых телах. — М.: Наука, 1981.
Выборное Б. И. Ультразвуковая дефектоскопия. — М.: Металлургия, 1974. Гаврилов Л. Р., Цирульников Е. М. Фокусированный ультразвук в физиологии и медицине.—Л.: Наука, 1980.
Гаврилов Л. Р. Применение докусированного ультразвука в медицине и физиологии.—Л.: изд-во ЦНИИ «Румб», 1978.
Гаврилов Л. Р. Применение фокусированного ультразвука для введения информации по различным сенсорным каналам.—Л.: изд-во ЦНИИ «Румб», 1984. Гершгал Д. А., Фридман В. М. Ультразвуковая технологическая аппаратура. — М.: Энергия, 1976.
Гик Л. Д. Акустическая голография. — Новосибирск: Наука, 1981. Глозман И. А. Пьезокерамика.—М.: Энергия, 1972.
Голямина И. П. Ультразвуковая хирургия. — В кн.: 10-я Всесоюзная акустическая конференция: Пленарные докл. — М.: 1983, с. 124—135.
Горелик Г. С. Колебания и волны: Введение в акустику, радиофизику и оптику. — М.—Л.: Гостехиздат, 1950.
Грегуш П. Звуковидение. — М.: Мир, 1982.
Гутин Л. Я. Избранные труды.—Л.: Судостроение, 1977.
Домаркас В. И., Кажис Р.-И. Ю. Контрольно-измерительные пьезоэлектрические преобразователи. — Вильнюс: Минтис, 1975.
Домаркас В. И. Пилецкас Э. Л. Ультразвуковая эхоскопия. — Л.: Машиностроение, 1988.
Ермолов И. Н. Теория и практика ультразвукового контроля. — М.: Машиностроение, 1981.
Журавлев А. И., Акопян В. Б. Ультразвуковое свечение. — М.: Наука, 1977. Загреков И. А. Эхо-энцефалография в неотложной нейрохирургии. — М.: изд-во М3 СССР, 1978.
Зарембо Л. К., Красильников В. А. Введение в нелинейную акустику. — М.: Наука, 1966.
Зарембо Л. К., Тимошенко В. И. Нелинейная акустика. —- М.: изд-во МГУ, 1984. Зарецкий В. В., Бобков В. В., Ольбинская Л. И. Клиническая эхо-кардиография: Атлас.— М.: Медицина, 1979.
Исакович М. А. Общая акустика. — М.: Наука, 1973.
Источники мощного ультразвука. Под ред. Л. Д. Розенберга. — М.: Наука, 1967. Каневский И. Я. Фокусирование звуковых и ультразвуковых волн. — М.: Наука, 1977.
Карлов В. А., Карахан В. Б. Ультразвуковая томография головного мозга и позвоночника. — Киев: Здоровья, 1980.
Клюкин И. И., Колесников А. Е. Акустические измерения в судостроении. — Л.: Судостроение, 1982.
Кнэпп Р., Дейли Дж. Хэммит Ф. Кавитация. — М.: Мир, 1974. Колесников А. Е. Ультразвуковые измерения. — М.: Изд-во стандартов, 1982. Королев М. В., Карпелъсон А. Е. Широкополосные ультразвуковые пьезопреобразо-ватели. — М.: Машиностроение, 1982.
Королев М. В. Эхо-импульсные толщиномеры.—М.: Машиностроение, 1980. Красильников В. А., Крылов В. В. Введение в физическую акустику. — М.: Наука, 1984.
Крауфорд Ф. Волны. — М.: Мир, 1984. / Лепендин Л. Ф. Акустика. — М.: Высш. шк., 1978.
Лихтерман Л. Б. Ультразвуковая томография и тепловидение в нейрохирургии. — М.: Медицина, 1983.
Михайлов И. Г. Соловьев В. А., Сырников Ю. П. Основы молекулярной акустики. — М.: Наука, 1964.
Маргулис М. А. Основы звукохимии (химические реакции в акустических полях). — М.: Высш. шк., 1984.
Мармур Р. К. Ультразвуковая терапия и диагностика глазных заболеваний. — Киев, Здоров'я, 1974.
Молчанов Г. И. Ультразвук в фармации. — М.: Медицина, 1980.
Матаушек И. Ультразвуковая техника.—М.: Металлургиздат, 1962. Мощные ультразвуковые поля /Под ред. Л. Д. Розенберга. — М.: Наука, 1968. Мухарлямов Н. М, Беленков Ю. Н. Ультразвуковая диагностика в кардиологии. — М.: Медицина, 1981.
Николаев Г. А., Лощилов В. И. Ультразвуковая технология в хирургии. — М.: Медицина, 1980.
Новиков Б. К., Руденко О. В., Тимошенко В. И. Нелинейная гидроакустика. — Л.: Судостроение, 1981.
Новые ультразвуковые методы и приборы для применения в биологии и медицине: Тезисы докл. Всесоюзн. совещания.—М.: изд-во АН СССР, 1986.
Добавлена при переводе. — Прим. ред.
Обработка изображений и цифровая фильтрация /Под ред Т. Хуанга. — М.: Мир, 1979.
Обработка изображений: Тематический выпуск. — ТИИЭР, 1981, т. 69, № 5. Основы физики и техники ультразвука /Б. А. Агранат, М. Н. Дубровин, Н. Н. Хавский и др.—М.: Высш. шк., 1987.
Остроумов Г. А. Основы нелинейной акустики.—Л.: изд-во ЛГУ, 1967. Перник А. Д. Проблемы кавитации. — Л.: Судостроение, 1966. Персианинов Л. С, Демидов В. И. Ультразвуковая диагностика в акушерстве: Атлас. — М.: Медицина, 1982.
Петровский Б. В.. Петров В. И., Лощилов В. И. Ультразвуковая резка и сварка биологических тканей. — М.: Медицина, 1972.
Рецепция и фокусированный ультразвук /Л. Р. Гаврилов, Г. В. Гершуни, О. Б. Ильинский и др.—Л.: Наука, 1976.
Ржевкин С. Н. Курс лекций по теории звука. — М.: изд-во МГУ, 1960. Римский-Корсаков А. В. Электроакустика.—М.: Связь, 1973.
Розенберг Л. Д. Визуализация ультразвуковых изображений. — Вестн. АН СССР, 1958, № 13, с. 33—43.
Розенберг Л. Д. Звуковые фокусирующие системы. — М.—Л., изд-во АН СССР, 1949.
Романенко Е. В. Физические основы биоакустики. — М.: Наука, 1974. Руденко О. В. у Солуян С. И. Теоретические основы нелинейной акустики. — М.: Наука, 1975.
Сарвазян А. П. Некоторые общие вопросы биологического действия ультразвука. Препринт. — Пущино: 1981.
Свет В. Д. Методы акустической голографии.—Л.: изд-во ЦНИИ «Румб», 1976. Сенсорное восприятие: Опыт исследования с помощью фокусированного ультразвука / И. А. Вартанян, Л. Р. Гаврилов, Г. В. Гершуни и др.—Л.: Наука, 1985. Скучик Е. Основы акустики. В 2-х томах. — М.: Мир, 1976.
Системы акустического изображения / Под ред. Г. Уэйда. —Л.: Судостроение, 1981. Смажевская Е. Л, Фельдман Н. Б. Пьезоэлектрическая керамика. — М.: Сов. радио, 1971.
Соколов С. Я. Ультразвуковые колебания и их применения. — ЖТФ, 1935, т. 2, с. 522—534.
Соколов С. Я. Ультразвуковой микроскоп. — ДАН СССР, 1949, т. 64, с. 333—336. Сперанский А. П., Рокитянский В. И. Ультразвук и его лечебное применение. — М.: Медицина, 1970.
Тюлин В. Н. Введение в теорию излучения и рассеяния звука. — М.: Наука, 1976. Улащик В. С. Введение в теоретические основы физической терапии. — Минск, Беларусь, 1981.
Улащик B.C., Чиркин А. А. Ультразвуковая терапия.—Минск: Беларусь, 1983. Ультразвук в биологии и медицине. УБИОМЕД-V: Тезисы докл. Междунар. симп. — Пущино: изд-во АН СССР, 1981.
Ультразвук в оториноларингологии / Под ред. А. И. Цыганова. — Киев: Наукова думка, 1978.
Ультразвук в терапии злокачественных опухолей / К. П. Балицкий, И. Г. Векслер, О. Е. Придатко и др. — Киев: Наукова думка, 1977.
Ультразвук в физиологии и медицине: Тезисы I научн. конф. В 2-х томах. — Ростов-на-Дону: изд-во АН СССР, 1972.
Ультразвук в физиологии и медицине: Тезисы докл. III Всесоюзн. конф. — Ташкент: изд-во Минздрава СССР, 1980.
Ультразвук в хирургии: Сборник статей, вып. 1 / Под ред. Г. А. Николаева, В. И. Лощилова.-М.: изд-во Минвуза, МВТУ, 1973.
Ультразвук и другие виды энергии в хирургии: Соорник статей, вып 2 / Под ред. Г. А. Николаева, В. И. Лощилова.-М, изд-во Минвуза, 1979
Ультразвук. Маленькая энциклопедия / Под ред. И. П. Голяминои. - М 1979. Ультразвуковая диагностика: Сборник научных трудов. - Горький: изд-во АН СССР 1983
Ультразвуковые преобразователи / Под ред. Е. Кикучи.-М.: Мир, 1972 Ультразвуковые преобразователи для «разрушающего контроля / Под ред. И Н Ермолова. — М.: Машиностроение, 1986. Физические основы ультразвуковой технологии / Под ред. Л. Д. Розенберга. - М..
Наука, 1970.
Фридман Ф.Е. Ультразвук в офтальмологии. - М.: Медицина, 1973. Харкевич А. А. Спектры и анализ. - М.: Физматгиз, 1952.
Харкевич А. А. Теория электроакустических преобразователей: Волновые процессы. - М.: Наука, 1973.
Харкевич А. А. Избранные труды. — М.: Наука, 1973, т. 1.
Чиркин А. А., Богданович Л. И., Улащик В. С. Ультразвук и реактивность организма. — Минск: Наука и техника, 1977.
Шрайбер Д. С. Ультразвуковая дефектоскопия. - М.: Металлургия 1965. Шутилов В. А. Основы физики ультразвука. - Л.: изд-во ЛГУ, 1980. Эльпинер И. Е. Ультразвук: Физико-химическое действие. - М.: Физматгиз, 1963. Эльпинер И. Е. Биофизика ультразвука. — М.: Наука, 1973.
В данном приложении собраны значения основных символов, используемых в этой книге, с указанием номера формулы (в круглых скобках) или раздела (в квадратных скобках), где они впервые введены или определены. Символы, которые вводились для описания какого-либо конкретного ограниченного вопроса и на которые отсутствуют ссылки где-либо еще в книге, в основном не приведены. Достигнуть исчерпывающего описания всех обозначений весьма затруднительно, особенно в книге, написанной несколькими авторами. Поэтому цель данного приложения направить читателя к первоначальным определениям символов, значения которых могут быть непонятны при их последующем использовании. За некоторыми оговоренными исключениями используемые обозначения соответствуют рекомендованным Международной организацией стандартов (ISO) для использования в акустике (публикация ISO от 31 июля 1978 г.).
![]() радиус (например, рассеивателя), длина а средний размер, радиус корреляции
радиус (например, рассеивателя), длина а средний размер, радиус корреляции
![]() ускорение частицы (1.176)
ускорение частицы (1.176)
![]() константа, постоянная затухания (4.32)
константа, постоянная затухания (4.32)
![]() скорость звука
скорость звука
![]() скорость звука (только для условий линейного распространения) (4.44)
скорость звука (только для условий линейного распространения) (4.44)
![]() линейный размер
линейный размер
![]() френелевская длина (2.3)
френелевская длина (2.3)
![]() расстояние задержки возбуждения (1.83)
расстояние задержки возбуждения (1.83)
![]() смещение частицы (1.175)
смещение частицы (1.175)
![]() напряжение холостого хода (3.28)
напряжение холостого хода (3.28)
![]() частота, какая-либо функция
частота, какая-либо функция
![]() функция Грина, ускорение свободного падения
функция Грина, ускорение свободного падения
![]() импульсный отклик (11.84)
импульсный отклик (11.84) ![]()
![]() ток
ток
![]() единичные координатные векторы
единичные координатные векторы
![]() волновое число:
волновое число:
![]() для гармонических волн, (1.123)
для гармонических волн, (1.123)
целое число или константа,
теплопроводность (12.6)
![]() характерный размер (1.81)
характерный размер (1.81)
![]() масса
масса
![]() целые числа
целые числа
![]() длина импульса в половинах длины волны (1.102)
длина импульса в половинах длины волны (1.102)
![]() коэффициент преломления (4.40)
коэффициент преломления (4.40)
![]() возмущение давления (звуковое или акустическое давление)
возмущение давления (звуковое или акустическое давление)
![]() статическое (внешнее) давление (1.2)
статическое (внешнее) давление (1.2)
![]() расстояние (скалярная величина) (1.39)
расстояние (скалярная величина) (1.39)
коэффициент отражения (по энергии) радиус (1.180)
расстояния от источника до импульса (1.86; 1.87)
![]() радиус сферического источника (1.46; 2.4)
радиус сферического источника (1.46; 2.4)
![]() пространственные координаты рассеивателя (6.6)
пространственные координаты рассеивателя (6.6)
![]() переменная при преобразовании Лапласа; (1.23)
переменная при преобразовании Лапласа; (1.23)
![]() время (1.3)
время (1.3)
![]()
![]() скорость,
скорость,
скорость частиц
![]() амплитуда напряжения сигнала (1.17)
амплитуда напряжения сигнала (1.17)
![]() декартовы координаты
декартовы координаты
![]() размер решетки (1.94)
размер решетки (1.94)
или апертуры, (1.167)
амплитуда ускорения частицы (1.7.1)
амплитуда релаксации, (4.11)
постоянная интегрирования
![]() функция движения поршня (6.53)
функция движения поршня (6.53)
![]() длина (1.99)
длина (1.99)
![]() характеристика чувствительности
характеристика чувствительности
приемного преобразователя (11.20)
![]() постоянная интегрирования, [7 3 11
постоянная интегрирования, [7 3 11
оптическая яркость (1.193)
![]() параметр нелинейности (4.31)
параметр нелинейности (4.31)
![]() удельная теплоемкость, (4.31)
удельная теплоемкость, (4.31)
контраст изображения, [7.3.1]
амплитуда смещения частиц [1-71] (12.34)
![]() длина, (1.93)
длина, (1.93)
ширина пучка (2.5)
![]() температуропроводность, (12.8)
температуропроводность, (12.8)
производительность дипольного источника (11.6)
![]() плотность энергии (1.22)
плотность энергии (1.22)
![]() опорная частота,
опорная частота,
некоторая функция
![]() сила (например, радиационная (1.212)
сила (например, радиационная (1.212)
![]() радиационная сила, действующая на плоскую поверхность (3.34)
радиационная сила, действующая на плоскую поверхность (3.34)
![]() радиационная сила, действующая на коническую поверхность (3.25)
радиационная сила, действующая на коническую поверхность (3.25)
![]() фурье преобразование
фурье преобразование
![]() фактор усиления, (4.51)
фактор усиления, (4.51)
некоторая функция,
модуль сдвиговой упругости (4.15)
![]() передаточная функция
передаточная функция
![]() частотная характеристика (11.88)
частотная характеристика (11.88)
![]() акустическая интенсивность (1.21; 1.38; 1.50; 1.68)
акустическая интенсивность (1.21; 1.38; 1.50; 1.68)
![]() средняя по времени интенсивность (1.75 — 1.77)
средняя по времени интенсивность (1.75 — 1.77)
![]() якобиан, (1.141)
якобиан, (1.141)
параметр взаимности в сферической волне (3.3)
![]() функция Бесселя
функция Бесселя
![]() модуль объемной упругости (4.15)
модуль объемной упругости (4.15)
![]() волновой вектор (1.125)
волновой вектор (1.125)
![]() длина,
длина,
длина импульса,
светимость [7.3.2]
![]() масса, (1.82)
масса, (1.82)
чувствительность гидрофона по напряжению
в свободном поле, (3.2)
модуль продольной упругости, (4.15)
показатель качества (для контактной жидкости [9.7] в акустической микроскопии)
![]() целое число
целое число
![]() автокорреляционная функция (6.48)
автокорреляционная функция (6.48)
![]() амплитуда акустического давления [1.7.1]
амплитуда акустического давления [1.7.1]
![]() амплитуда падающих и рассеянных волн (6.7)
амплитуда падающих и рассеянных волн (6.7)
![]() коэффициент отражения по давлению, (1.178) радиус,
коэффициент отражения по давлению, (1.178) радиус,
расстояние от сферического источника, (1.46)
газовая постоянная (4.38)
![]() расстояние от источника до фокуса (1.93)
расстояние от источника до фокуса (1.93)
![]() расстояние (1.-84)
расстояние (1.-84)
![]() площадь поверхности, (1.18)
площадь поверхности, (1.18)
отклик по току гидрофона, (3.1)
производительность монопольного источника (11.13)
![]() площадь акустического излучателя [4.4.2.1]
площадь акустического излучателя [4.4.2.1]
![]() площадь акустического приемника (4.51)
площадь акустического приемника (4.51)
![]() доплеровский спектр мощности (11.49)
доплеровский спектр мощности (11.49)
![]() коэффициент пропускания по давлению, (1.179)
коэффициент пропускания по давлению, (1.179)
импульсный отклик ткани (6.62)
![]() поверхностное натяжение (4.31)
поверхностное натяжение (4.31)
![]() автокорреляционная функция импульсного отклика ткани (6.72)
автокорреляционная функция импульсного отклика ткани (6.72)
![]() тензор второго порядка (1.189)
тензор второго порядка (1.189)
![]() амплитуда и (4.1)
амплитуда и (4.1)
![]() объем,
объем,
амплитуда колебательной скорости частиц [1.7.1]
скорость движения (источника, наблюдателя) (11.1)
![]() объемная концентрация (частиц) (4.30)
объемная концентрация (частиц) (4.30)
![]() напряжение, изменяющееся во времени
напряжение, изменяющееся во времени
![]() акустическая мощность (1.154)
акустическая мощность (1.154)
(заметим, что ISO для этой величины рекомендует символ Р)
![]() безразмерная функция для описания радиационной
безразмерная функция для описания радиационной
силы, действующей на сферу [3.4.2]
![]() удельный акустический импеданс (1.178)
удельный акустический импеданс (1.178)
![]() коэффициент затухания (4.1)
коэффициент затухания (4.1)
![]() фазовые углы (1.154)
фазовые углы (1.154)
![]() сжимаемость (
сжимаемость (![]() — средняя, (6.1)
— средняя, (6.1) ![]() — флуктуации)
— флуктуации)
переменная интегрирования (1-49)
![]() постоянная распространения, (1.125)
постоянная распространения, (1.125)
степень фокусировки преобразователя, (2.4)
![]() , (1.64)
, (1.64)
обобщенная величина деформации, (4.20)
отношение теплоемкостей (для газа) (4.31)
![]() функция Дирака (1.128) противолежащий угол (8.3)
функция Дирака (1.128) противолежащий угол (8.3)
![]() длина, (1.83) коэффициент вязкости (4.12) (
длина, (1.83) коэффициент вязкости (4.12) (![]() — сдвиговая вязкость,
— сдвиговая вязкость, ![]() — объемная вязкость)
— объемная вязкость)
![]() угол
угол
![]() константа (11.26)
константа (11.26)
![]() длина волны
длина волны
![]() коэффициент затухания и т.п. (сечение на единичный объем)
коэффициент затухания и т.п. (сечение на единичный объем)
для среды (4.2), (6.23)
(![]() — затухание,
— затухание,
![]() — поглощение,
— поглощение,
![]() — общее рассеяние,
— общее рассеяние,
![]() — дифференциальное рассеяние,
— дифференциальное рассеяние,
![]() — обратное рассеяние)
— обратное рассеяние)
![]() плотность среды
плотность среды
(![]() — средняя, (1.1)
— средняя, (1.1)
![]() —флуктуации) (6.1)
—флуктуации) (6.1)
![]() сечение рассеивателя [4.1], (6.21)
сечение рассеивателя [4.1], (6.21)
(![]() — сечение затухания,
— сечение затухания,
![]() — сечение рассеяния,
— сечение рассеяния,
![]() — сечение поглощения),
— сечение поглощения),
поверхность, (1.136) обобщенная величина упругого напряжения, (4.20)
коэффициент поверхностного натяжения (12.13) ![]() (1.2)
(1.2)
коэффициент передачи энергии, (1.181) время релаксации (4.22)
(![]() — сдвиговой,
— сдвиговой,
![]() — объемной)
— объемной)
![]() потенциал скорости (1.7) угол
потенциал скорости (1.7) угол
![]() теплопроводность (4.31)
теплопроводность (4.31)
![]() круговая частота
круговая частота
|
Доза биологически эффективная 117—119 Заживление ран 505—508 Закон Рэдея 146, 267, 385, 386
Замораживание тканей, эффект 195, 196 «Затенение» 351 Затухание звука 125—127 в биологических тканях 166 аспекты характе- ризации 378 измерение 166 пространственное распределение 174 в твердом теле 144, 146 дисперсия 207, 209, 237, 238 зависимость от внешнего давления 151 от кавитации 161, 162 от нелинейности 154—161 от структуры ткани | |||
Кислоты нуклеиновые 402, 425, 426 Линзы акустические 77—79 133-140 140—144 144—146 104 Митохондрии 512, 513, 532 |
Преобразователь для ультразвуковой терарии 503 Приближение Борна 262, 265 266 405, 406 404—406 Рассеяние звука 125, 151, 270 181, 206—209 283—285 | |||




